基于局部特征尺度分解及分形维数的模拟电路故障诊断方法

盛 沛，许爱强，徐学文，李 恒

（海军航空大学，山东烟台264001）

当前，以神经网络法[1]、模糊理论[2]、专家系统[3]、遗传算法[4]等为代表的跨学科研究方法越来越多地被引入到模拟电路故障诊断技术中。虽然这些方法与传统时频分析方法相结合，已取得诸多成果，但却存在缺乏自适应性这一共性问题[5]。在自适应时频分析方法中，目前国际上研究和应用最为广泛的是基于经验模态分解（Empirical Mode Decomposition，EMD）和Hilbert 变换的希尔伯特- 黄变换[6-7]（Hilbert-Huang Transform，HHT）及其改进算法[8-9]，其优点是适用于非线性、非平稳信号的分析。虽然在一定程度上克服了传统时频分析方法的一些不足之处，但是EMD 在使用过程中也存在一些诸如模态混叠、端点效应等问题。为进一步解决上述问题，2012 年，湖南大学的程军圣、杨宇团队提出了局部特征尺度分解方法[10-13]（Local Characteristic-scale Decomposition，LCD），该方法在滚动轴承诊断领域已经取得了较好的成果，但是在模拟电路故障诊断领域，尚未有人做出尝试。究其原因，是在对故障波形做LCD 分解之后，还缺乏一种有效的工具将其与故障状态联系起来，即故障特征的提取。

2010年，李伟等提出一种以模拟电路分形特征为输入量的故障诊断方法[14]。2017年，哈尔滨理工大学吕鑫淼等人在此基础上将该方法与支持向量机相结合[15]，实现了对模拟电路软故障的简单分类。但是该方法实测结果较为粗略，易产生混叠。究其原因，是将原始待测信号不加处理地直接进行分形维数计算，达不到从不同角度、不同层次刻画模拟电路故障状态的目的。

本文针对上述问题，提出一种LCD与分形维数理论相结合的方法，对模拟电路进行故障诊断，在给出理论方法的基础上，进行了仿真分析和实物验证。

1 LCD算法原理

LCD 方法主要步骤是不断寻找均点及构造均值曲线，并将其从信号中剥离，直至信号为“内禀尺度分量（Intrinsic-Scale Component，ISC）”。该算法在采用线性方法估计包络曲线时，没有考虑其上凸或者下凹的特性，这必然造成信息的丢失，如图1中的阴影部分所示。

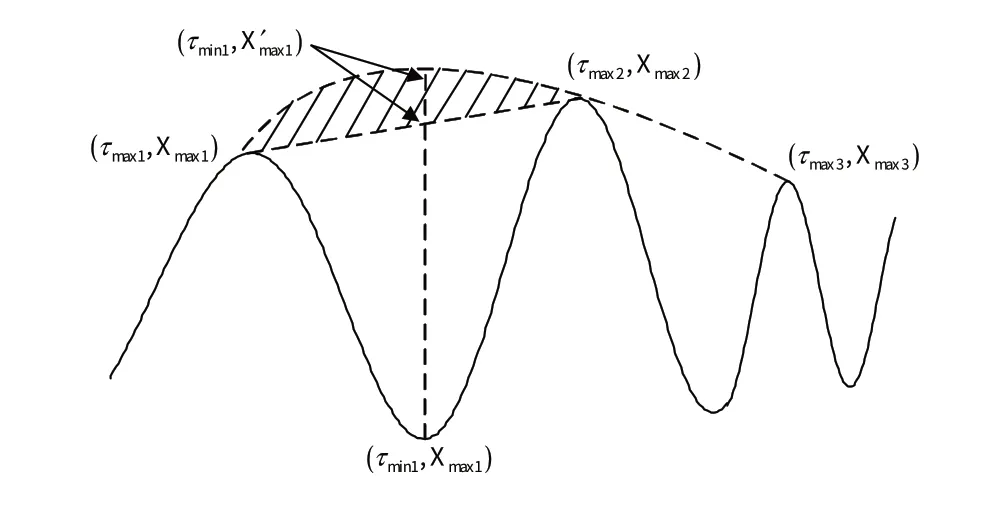
图1 改进的均值曲线构造方法Fig.1 Improved constructing method of mean value curve

本文在文献[10]算法的基础上略做改进，在计算极值点对应的均值点时，将该极值点和相邻3 个不同类型的极值点作为计算条件，以提高均值点的估计精度[16]：

2 LCD与分形维数相结合的故障诊断方法

2.1 方法思路

对于模拟电路故障诊断而言，在测点较少、电路模型复杂的情况下，准确提取故障特征是故障诊断所要解决的首要问题。其各种故障现象往往与其运行状态存在着对应的联系。如果将电路的每一次故障状态当作一个样本，那么同一故障在某些特征上将会表现出一定的共性。

分形是用来刻画对象的不规则性和自相似性的一种理论，在处理复杂非线性系统中具有独到之处。运用分形理论准确提取出故障特征，不仅可以定性，而且可以定量地描绘出系统的工作状态，从而实现故障诊断的目的。

因此，本文提出一种将LCD与分形维数相结合的诊断方法。通过LCD，将原本一维的待测样本变成多个具有物理意义[10]的ISC 分量。与原始信号一样，这些分量中的某一个或者某几个也必然与故障状态存在着强弱不同的联系。对这些ISC 分量进行分形维数计算得到一组故障特征后，便可以借助神经网络将这些强弱不同的联系体现出来，达到精准刻画故障状态的目的。

分形维数的计算方法很多，本文选取计算量较小的计盒维数法：用边长r 的小盒子覆盖待测曲线，统计非空小盒子的数量并将其记为N(r)，若缩小盒子的尺寸，则N(r)必然随之增大。据此，可得分形维数[17]

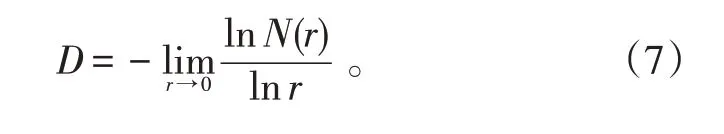
2.2 诊断步骤

基于上述对故障特征提取的思路，利用BP 神经网络，即可完整地对模拟电路进行故障诊断。具体步骤如下。

步骤5：将训练样本归一化后，作为输入向量完成对选定神经网络的训练。

步骤6：重复步骤2、3，将特征向量输入训练好的神经网络，即可判断待测设备故障模式。

3 实例验证

3.1 仿真验证

为了验证方法的有效性，选用某雷达发射机模拟电路中开关电源部分作为验证对象[18-19]，仿真平台ORCAD17.2 和Matlab16.2。仿真模拟电路如图2 所示，状态集如表1所示。

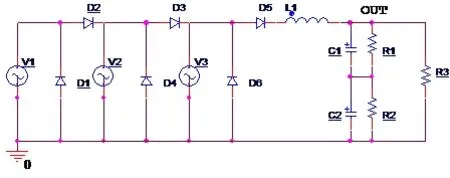
图2 仿真模拟电路Fig.2 An analog circuit

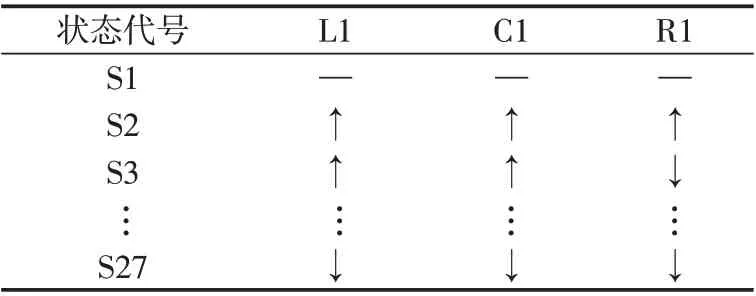
表1 电路状态集合Tab.1 Circuit state set

在27 种电路状态中，各随机采集50 次测试节点电压信号，经上述处理后，共得到1 350 组特征向量。归一化后，输入训练好的BP 神经网络，进行故障诊断。经多次试验，结果表明当网络结构为6-33-30-27时效果最优。其中，输入向量由原始信号盒维数及前5 个ISC 分量盒维数组成，输出对应着27 个状态序号。为比较该算法性能，将EMD、LMD算法一并纳入考察范围。某组典型仿真数据分解结果如图3 所示，全部诊断结果如图4所示。

从分解结果看，LCD 方法的端点效应不明显，LMD 方法稍差，EMD 方法最差。这是由于LCD 方法对均值点进行插值获得均值曲线，迭代次数少；而EMD方法每求取一次均值曲线要插值两次，且插值的时间间隔大。

从诊断结果看，LCD 方法平均正确率最高为92.96%；LMD 方法稍差，为91.74%，但离散性较大；EMD最差，为88.59%。分析其原因，是由于在确定分解层数时无法对3种方法做统一要求，在舍弃分量时，致使原始信号信息量丢失。

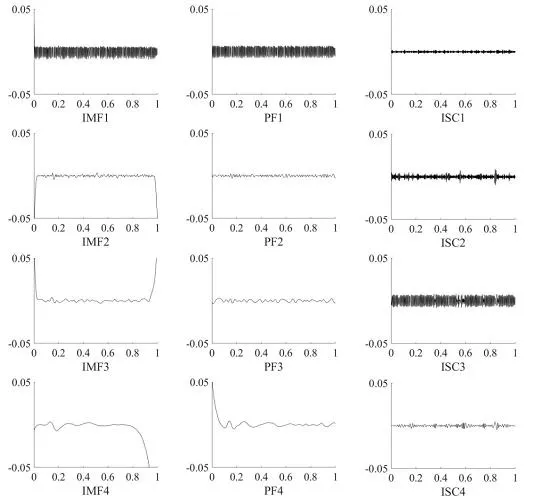
图3 某组仿真数据各算法分解结果Fig.3 Decomposition results of a set of simulation data by each algorithm

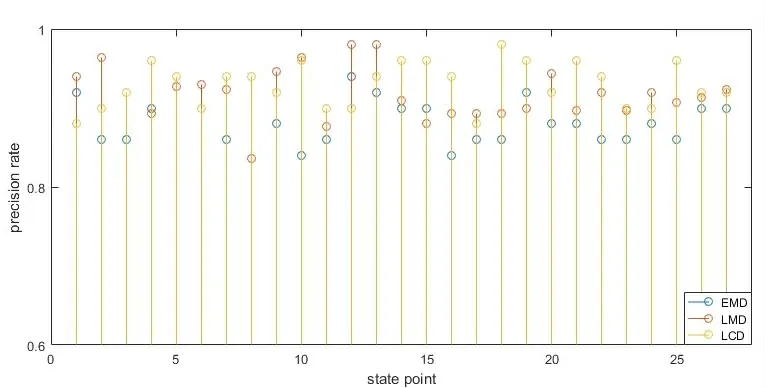
图4 诊断结果比较Fig.4 Comparison of diagnostic results

3.2 实物验证

上述仿真实验是建立在模型已知、参数可调、无噪声干扰的理想条件下。在实际应用中，噪声等因素对诊断结果也会有较大干扰。本文采用汉泰公司生产的DSO-3062L虚拟示波器进行数据采集，上位机运行环境WindowsXP3，编译软件LABVIEW8.5，联合Matlab7.0服务程序编程。实验步骤如下。

步骤1：选取某导引头模拟电路中一可调电阻作为实验对象。

步骤2：给待测设备施加激励信号，调节电阻值2次，各采集测试节点输出1 000 次信号Vi。

步骤3：将输出信号Vi做LCD 分解。求取前5 个ISC 分量的分形维数及原始信号分形维数，不足5 个的用0补齐，组成特征向量。

步骤4：将获得的特征向量及对应的阻值做归一化处理，并分别作为输入向量及输出目标值。

联合Matlab 服务的测试程序分类结果如图5 所示。

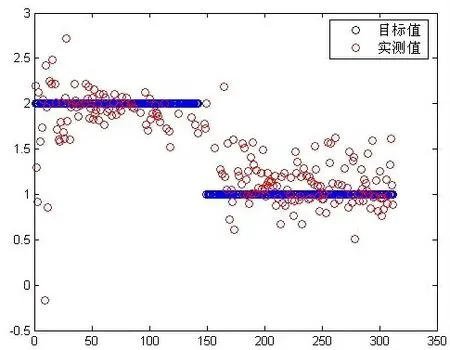
图5 分类结果Fig.5 classification results

由诊断结果可以看到：故障现象可以有效分类。诊断结果野点较多，分析其原因是部分采集数据在LCD后出现较大的端点效应。以图6某时刻所采数据的实时LCD分解结果（缩放图如图7所示）为例，可以看到，第2分量在0.002 5 s 前有较大端点效应。

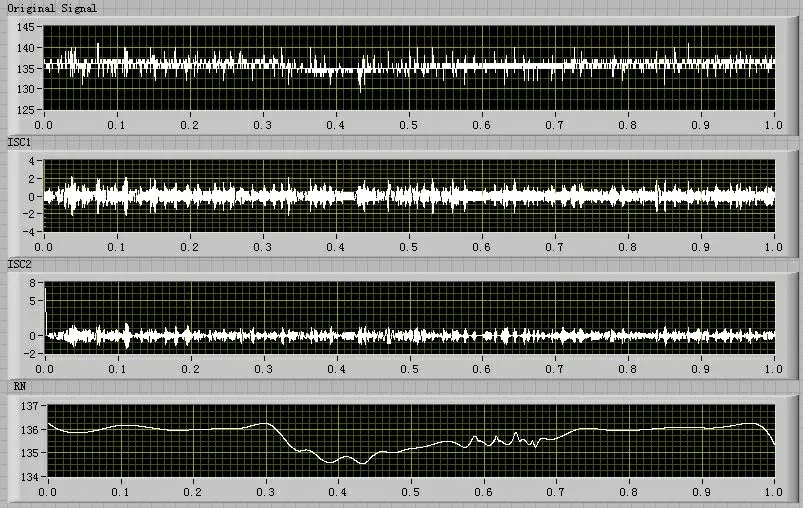
图6 LABVIEW实时采集数据截图Fig.6 LABVIEW collects of data screenshots in real time

图7 第二分量局部放大图Fig.7 Local magnification of the second component

须要说明的是，上述实验过程可分为2个阶段：一是基于示波器及Labview平台的数据采集和预处理过程；二是在Labview 中调用Matlab 服务对数据进行算法分解及结果显示过程。由于受试验用仪器采样精度及噪声影响，所测电阻超差较小时，很难做到准确分类。

4 结束语

本文提出了一种将改进LCD 算法与分形维数相结合的模拟电路故障诊断方法。通过仿真实例证实了算法的有效性。在基于虚拟示波器的实际电路实验中，故障现象可以有效分类，但仍存在野点较多的问题。下一步将结合端点效应，抑制、剔除粗大值等方法进一步完善该算法，并将着重研究故障分类准确率随被测元件超差情况的变化规律。