DRO计算及其在地月系中的摄动力研究

吴小婧，曾凌川，巩应奎

（中国科学院空天信息创新研究院，北京100094）

随着深空探测任务的开展，有许多不同的关键技术需要研究，首先需要解决的关键问题就是航天器的轨道设计问题。相较于近地空间，深空探测器所处的引力环境具有多样性，不再局限于经典的二体开普勒轨道，其基本动力学模型可简化为一个受摄的圆形限制性三体问题（Circular Restricted Three-Body Problem，CRTBP）［1］。在CRTBP中，以地月（Earth-Moon，EM）系为例，由于地月系相较日地系，第二主天体的轨道偏心率更大、太阳作为第三引力体对地月系的引力影响更强烈，因此地月系三体轨道设计将面临更大挑战［2］。本文尝试以地月系为背景对远距逆行轨道（Distant Retrograde Orbit，DRO）设 计 做 初 步研究。

DRO属于圆形限制性三体问题中一类特殊的平面对称轨道［3］，其围绕较小主天体运动，在会合坐标系中，运行方向与主天体的公转方向相反，因此，轨道是逆行的。理想的周期DRO只存在于圆形限制性三体问题中，在实际力模型中，由于摄动力的影响，周期DRO变为拟周期DRO［4-5］。当这些拟周期轨道受到比其他三体轨道族更大的扰动时，仍能保持稳定［6-7］，因此非常适于深空导航组网、中继通信以及科学数据采集等任务。

NASA 曾计划在其木星冰月轨道任务（NASA’s Jupiter Icy Moon Orbiter，JIMO）中使用DRO来平衡木星和其卫星的引力摄动，该任务原计划于2015年左右发射［8］。NASA的小行星重定向任务（ARM）曾计划捕获一颗近地小行星［9-10］，并使用低推力航天器将其拖拽到DRO上［11］，由于DRO的长期稳定性，当受到如非对称引力场、太阳辐射压以及来自太阳系其他天体的引力等摄动时，在未来的几十年甚至更长时间，小行星都不需要位置保持机动［10，12］。学者们在基于DRO的深空探测方面也做了大量的研究工作。Ocampo和Rosborough提出利用日地系DRO构建太阳风暴预警系统的应用设想［13］，介绍了日地系中DRO的几种类型，并针对日地系DRO设计了脉冲转移轨道。针对此应用设想，Demeyer和Gurfil研究了从地球到日地DRO的转移轨道的设计方法［14］；Scott和Spencer利用微分校正法计算了转移到日地DRO的转移轨道族［15］。Stramacchia等提出利用日地DRO部署天基望远镜网络探测近地危险小行星的应用设想［16］。徐明与徐世杰提出了将中继卫星布置在地月DRO的设想［17］，研究了空间双圆模型下DRO的轨道稳定性，并研究了转移轨道的设计方法。Murakami和Yamanaka基于未来在月球附近建造一个新的空间站或燃料补给港的设想，对在地月DRO上的交会对接技术进行了研究［18］。Conte等对直接从近地轨道（Low Earth Orbit，LEO）转移到火星和采用月球DRO作为中转站转移到火星2种地火转移方式开展了比较研究［19］。这些研究均是在CRTBP模型下，并没有考虑月球的引力摄动。

此外，为了设计DRO，Lara用摄动分析方法得到了DRO的低阶解析解和高阶解析解［20］，并利 用 高 阶 解 析 解 计 算 了 DRO 周 期 轨 道［21］。Bezrouk和Parker研究了在长达数万年的时间里，地月系中几个不同大小的DRO的演化问题［22］。

以上研究主要针对需要完全放手、长时间隔离轨道的任务，例如火星样本返回任务或小行星重定向任务等对轨道精度要求不高的任务，而且高阶模型存在形式复杂和计算繁琐等不足。本文针对需要高轨道精度的深空导航和通信服务，着重高精度动力学模型的建立，通过数值方法研究了DRO的设计问题。

考虑到设计符合动力学环境需求的标称任务轨道不仅能有效地节省轨道保持的燃料［23］，而且可以为在轨导航制导提供理想的参考轨道。因此本文针对实际工程应用中标称任务轨道的设计问题，以地月系为背景，研究了DRO的设计方法，分析了在实际力环境下地月DRO拟周期轨道的轨道特性及主要摄动因素。首先，针对地月DRO的动力学特征，利用构造流函数法求解其周期轨道，并通过周期轨道在地月会合坐标系和地月惯性坐标系中的对应关系，从共振角度对DRO轨道特性进行了分析和总结；然后，在实际力模型下，研究地月DRO的主要摄动因素，在考虑太阳引力摄动和月球轨道偏心率摄动的星历模型中，分析地月DRO的非开普勒特征与稳定性。仿真研究表明，构造流函数法可以有效应用于DRO的数值求解，从而摆脱了经典微分校正法迭代初值对近似解析解的依赖，可以在近似解析解失效的更广大区域求得DRO周期轨道的数值解。不同于以往的研究，本文通过不同摄动力模型下DRO轨道特性的分析对比，得到影响地月DRO的主要摄动因素及其影响程度，可以为设计符合动力学环境需求的标称任务轨道提供理论依据。

1 动力学模型

1.1 坐标系定义

1）地月会合坐标系O-xyz。在圆形限制性三体条件下的地月会合坐标系O-xyz，其原点在地月系的质心O，x轴由质心指向月心方向，z轴指向系统角速度方向，y轴与x轴、z轴构成右手坐标系［24］。

2）地月惯性坐标系OE-XYZ。其原点在地球质心OE，月球在地月参考平面上绕地球作圆周运动，t＝0时刻，地月惯性坐标系和地月会合坐标系的轴线对齐，月球位于＋X轴上［24］。

1.2 圆形限制性三体问题

根据开普勒定律，假设地球和月球这2个主天体都可看成1个质点，它们围绕彼此作圆周运动。第3个小天体航天器，受主天体的引力影响，但不影响主天体的轨道。对各单位进行无量纲化处理，用两主天体的质量和作为单位质量，较小主天体的质量为m′。对于地月系，m′＝0.012 150 5。两主天体间的平均距离无量纲化为1。本文中采用的地月距离为384 400 km。

CRTBP地月会合坐标系会随着两主天体旋转，由于它们之间的距离是恒定的，所以这2个主天体在会合坐标系中看起来是静止的。无量纲化处理后，原点位于2个主天体的质心，2个主天体位于x轴上，较大主天体位于-μ处，较小主天体位于1-μ处，其中，μ＝m′＝0.012 150 5。z轴沿两主天体轨道的法向，y轴与x轴和z轴构成右手坐标系。对其进行无量纲化处理使得两主天体的轨道周期为2π。对于地月系，CRTBP的时间间隔2π对应于27.28 d。CRTBP的运动方程 为［24］

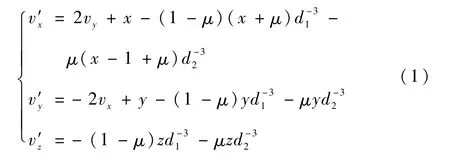
式中：

其中：d1、d2分别为航天器到两主天体的距离；r＝（x，y，z）为航天器的位置向量；v＝（vx，vy，vz）为速度向量。

CRTBP方程（1）有一个运动积分，被称为雅可比积分：

式中：

雅可比积分实际上是质点总能量的量度，雅可比积分越大，则质点能量越小，反之亦然。雅可比积分虽然不能确定质点的全部运动规律，但通过研究雅可比积分，仍能得到有关质点运动的丰富信息。

2 利用构造流函数法计算DRO

2.1 构造流函数法

由于限制性三体问题的非线性，目前只有依靠微分方程的数值解法才能得到满足实际任务精度要求的DRO周期解。经典的微分校正法是利用轨道的状态转移矩阵构造牛顿迭代过程的，迭代初值可以由CRTBP的线性化模型给出，也可利用Lindstedt-Poincaré摄动分析方法得到更高阶的初值。本文针对地月DRO的动力学特征，利用构造流函数法求解其周期轨道。该方法的优点是不需要以近似解作为迭代初值，因此不受非线性的影响，可以在近似解析解失效的更广大区域求取周期轨道的数值解。

下面给出流函数的概念［25-26］。设系统式（1）以X（t0）＝X0为初始状态的解轨迹为φ（t，t0），则φ（t，t0）：X（t0）→X（t）定义了动力学系统式（1）的流映射，它将t0时刻的初始状态映射到t时刻状态。这里的φ被称为流函数。本文使用一种特殊的流函数，它能将初始状态X0映射到未来某时刻位于x轴上的另一状态，将其表示为φ（k，X0），其中k为流函数与x轴相交的次数，相对于φ以给定时间作为积分终止条件，则φ以与x轴的第k次相交作为终止条件。由于DRO属于平面圆形限制性三体问题［3］，因此系统状态向量可表示为X＝［x y vxvy］T，为了计算φ（k，X0）的值，引入如下判别函数：

由于DRO轨道具有沿X轴的对称性，其与X轴相交时必须满足垂直相交条件，即y方向速度为零。根据这个特征，判别函数具有简单形式，只是取状态X的y分量，且初始积分状态可以取为X0＝［x00 0 vy0］T。若限定雅可比积分为C，则根据雅可比积分公式可得

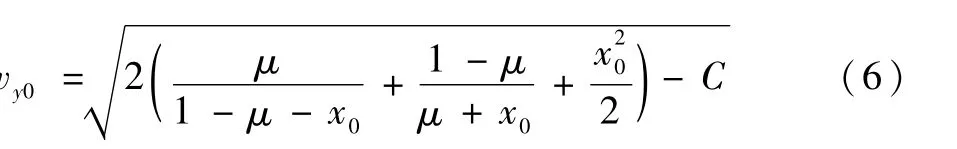
对初始状态X0逐步积分，并在每一步积分中计算判别函数的值，当其符号第k次发生改变时，表明流函数第k次跨越了x轴，这时以Crit（X）符号改变前后的t值作为初值，恰好可以应用Brent方法来解方程：

设解为t*，则

显然，φ（k，X0）的解算包含了一个数值积分和一个数值求根过程，虽然无法得到其解析表达式，却仍然可以用数值方法研究φ（k，X0）的性质。若以φvx表示φ的vx分量，则计算雅可比积分C下的DRO轨道等价于求解方程：

式中：φ*（x）为以x为自变量的轨迹函数在vx方向的分量。考虑到DRO属于圆形限制性三体问题中的平面对称轨道［3］，X表达式为

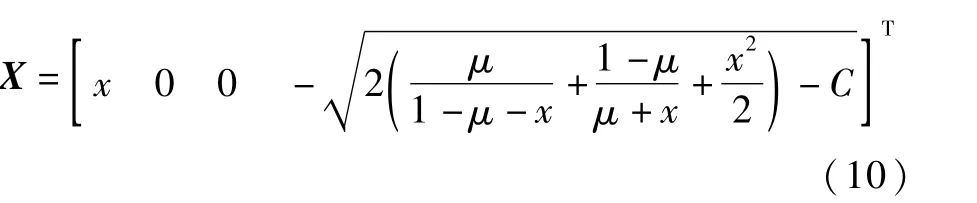
式（9）同样可以应用数值求根方法解出，迭代初值当然也可以由线性化解析解给出，但本文采用更方便的方法，即观察φ*（x）的曲线（见图1（a）），寻找其与x轴的交点，由图中得到交点P的近似坐标作为初值。图1（b）中L1和L2分别表示地月系的拉格朗日点L1、L2。

构造流函数法利用了CRTBP的对称性，它不但可以计算DRO轨道，而且可以系统地计算一大类具有x轴对称性的周期轨道，如图2所示。即利用构造流函数法计算了1 ∶3地球共振轨道在地月会合坐标系和地月惯性坐标系中的运动轨迹，在地月会合坐标系下的一个轨道周期里，航天器在地月惯性坐标系下环绕地球3圈，Re为地球半径。从图2可以明显看出，共振轨道在地月会合坐标系中是闭合的，其拱线在地月惯性坐标系中旋转。这类轨道可以看做地月系中绕地球旋转的DRO轨道。

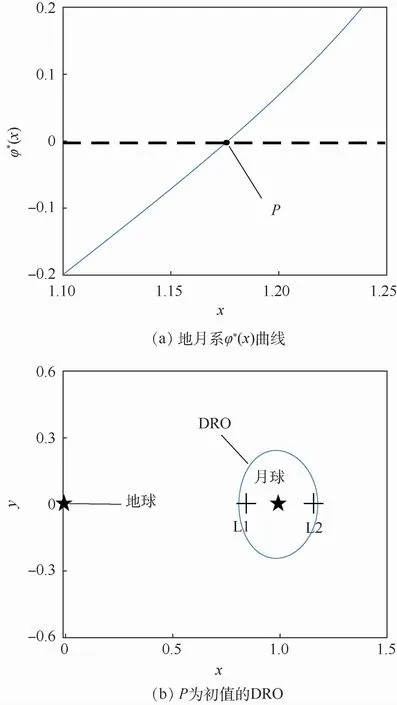
图1 地月系的φ*（x）曲线和以点P为初值迭代得到的DRO（C＝2.93）Fig.1 φ*（x）curve of the Earth-Moon system and DRO obtained by iteration with point P as initial value（C＝2.93）

2.2 DRO计算及其非开普勒特征分析

本文通过在圆形限制性三体模型下延拓雅可比积分C计算地月DRO周期轨道族。DRO存在较大的幅值范围，当幅值较小时，DRO完全可以看作低轨的环月轨道，此时，DRO具有较高的雅可比常数，接近L1（CL1＝3.18834）和L2（CL2＝3.17216）的雅可比常数。随着雅可比常数的减小，DRO幅值将逐渐增大，越靠近地球时对应的雅可比常数越小。图3在很大的范围内绘制了地月CRTBP中的DRO周期轨道族。每个轨道的颜色表示雅可比常数，由右边的颜色栏指定。很明显，一些轨道已经延伸到离月球很远的地方，因此被称为DRO。越靠近月球，DRO的周期越短，随着轨道周期通过与月球1∶4、1∶3和1∶2的共振，DRO的大小增加，并逐渐接近与月球1 ∶1的共振。

图2 地球DRO（1∶3）共振轨道Fig.2 The Earth resonant orbit of DRO（1∶3）

图3 DRO周期轨道族与雅可比常数CFig.3 DRO periodic family and Jacobi constant C

以上是在地月会合坐标系下对DRO进行了计算。然而，在航天器任务分析中，了解地月惯性坐标系解的性质是至关重要的。为此，本文定义了一个地月惯性参考框架，其具有以下性质：参考框架的坐标原点是地球，月球在地月参考平面上绕地球作圆周运动。在t＝0时刻，地月惯性坐标系和地月会合坐标系的轴线对齐。因此，在t＝0时刻，月球位于地月惯性坐标系的＋X轴上。由CRTBP的对称性可知，判别式（7）的解t*即为1／2轨道周期，联合式（9）和式（10）通过数值方法得到雅可比积分C与DRO轨道周期的对应关系，从而可找到1∶2、1 ∶3及1 ∶4的月球共振轨道，图4（a）、图4（b）、图4（c）分别展示了它们在地月惯性坐标系下的运动轨迹。从图4可以看出，这3种共振轨道均为非开普勒轨道，它们在地月惯性坐标系中是周期闭合的。图4（d）是共振比非整数的DRO在地月惯性坐标系中的运行情况，其轨迹不再是封闭的曲线，而看起来像是在月球轨道附近打水漂。

图4 DRO在地月惯性坐标系中的运动轨迹Fig.4 Motion trajectory of DRO in the Earth-Moon inertial coordinate system

3 摄动力模型下的DRO仿真分析

第2节DRO研究是基于圆形限制性三体模型的。本节研究地月摄动力模型下，DRO的动力学特性。地月系中，摄动因素主要包括太阳引力、太阳光压、月球非对称引力、其他行星的引力等。表1显示了以月球为中心的DRO所受加速度的种类及其近似量级。在实际力模型下，CRTBP中理想的周期DRO不再呈现周期性，运行轨迹为拟周期DRO。

为了衡量每种摄动对DRO动力学模型精度的影响，选用STK中的地月拟周期DRO轨道初值［x，y，z，vx，vy，vz］＝［155 932 km，0 km，0 km，0 km／s，-0.869 709 km／s，0 km／s］外 推1年，每 次 从高精度模型（考虑了月球非对称引力、木星引力、金星引力、太阳光压、太阳引力）中去掉一种摄动项，然后和高精度模型下的DRO拟周期轨道形态进行比较。具体模型如下所示。

表1 摄动平均量级Tab le 1 Average m agnitude of perturbation

模型1：高精度模型。

模型2：高精度模型中不考虑月球非对称引力。

模型3：高精度模型中不考虑木星引力和金星引力。

模型4：高精度模型中不考虑太阳光压。

模型5：高精度模型中不考虑太阳引力。

模型1～模型5的外推结果如图5所示。从图5可以看出，模型1到模型4，拟周期DRO形态无显著变化，到模型5，由于模型中去掉了太阳引力，拟周期轨道形态发生了显著变化。因此图5的仿真结果表明，太阳引力是影响拟周期DRO形态最主要的摄动因素，在实际工程建模中必须考虑太阳引力摄动的影响。

接下来通过模型1的高精度模型和模型2～模型5的各种摄动力模型的比较来分析各种摄动模型的轨道外推精度。具体的，对地月会坐标系中的x坐标、y坐标以及到月球距离在各种摄动模型与高精度模型之间做差，而后统计轨道差的均方差作为各种摄动模型轨道外推精度的估计值。图6为模型1和模型2的差值，即不考虑月球非对称引力摄动的动力学模型轨道外推精度；图7为模型1和模型3的差值，即不考虑木星、金星引力摄动的动力学模型轨道外推精度；图8为模型1和模型4的差值，即不考虑太阳光压的动力学模型轨道外推精度；图9为模型1和模型5的差值，即不考虑太阳引力的动力学模型轨道外推精度。

图5 摄动力模型下地月拟周期DROFig.5 The Earth-Moon quasi-periodic DRO under perturbative forcemodel

图6 模型1和模型2在x、y坐标及到月球距离的偏差Fig.6 Deviation of x，y coordinate and distance to the Moon between Model 1 and Model 2

图7 模型1和模型3在x、y坐标及到月球距离的偏差Fig.7 Deviation of x，y coordinate and distance to the Moon between Model 1 and Model 3

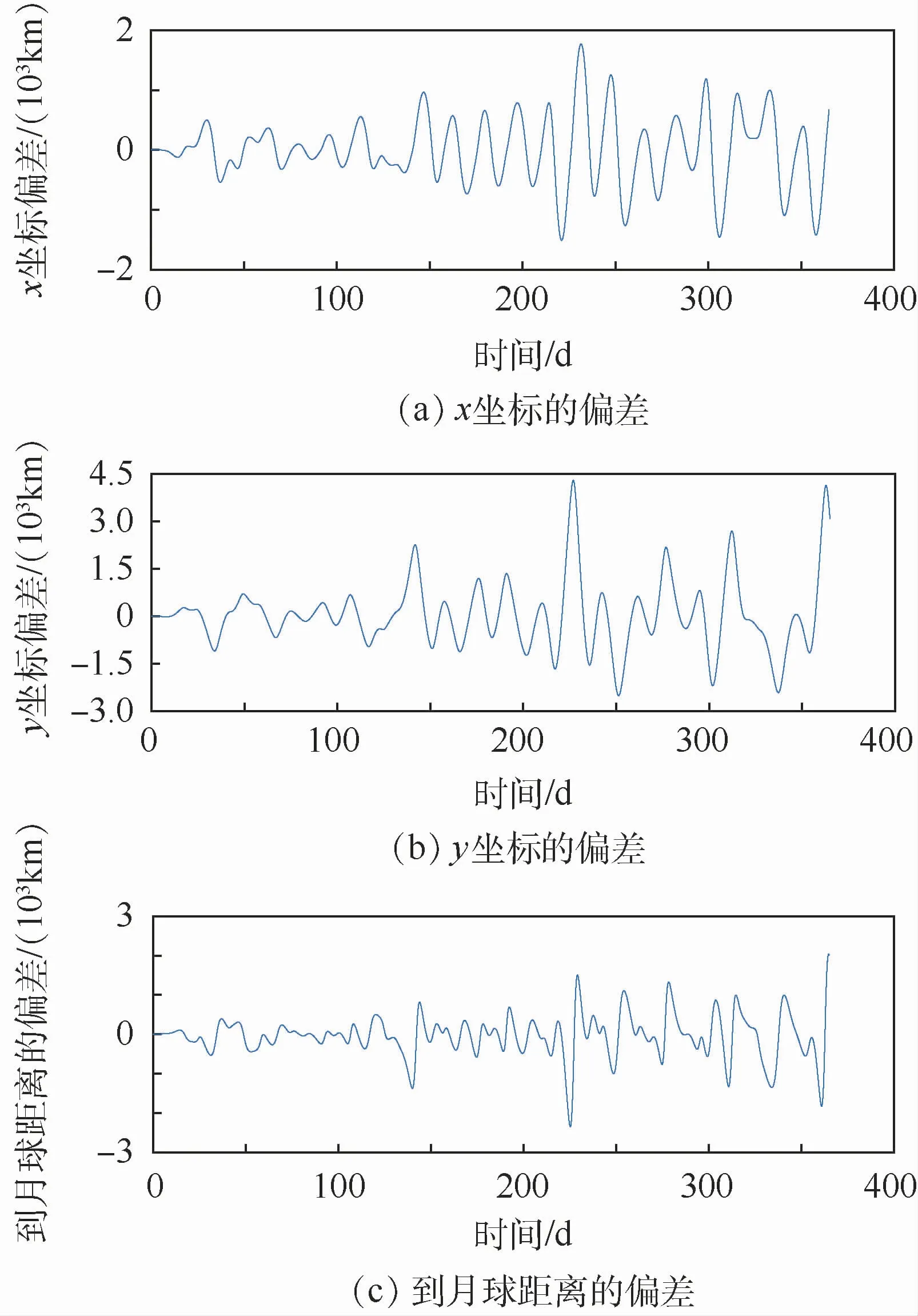
图8 模型1和模型4在x、y坐标及到月球距离的偏差Fig.8 Deviation of x，y coordinate and distance to the Moon between Model 1 and Model 4

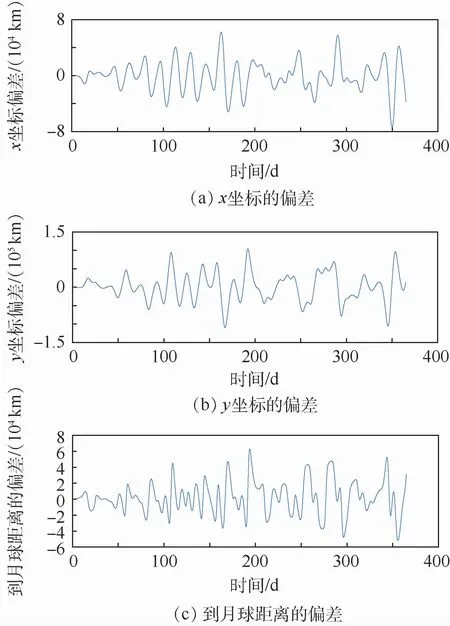
图9 模型1和模型5在x、y坐标及到月球距离的偏差Fig.9 Deviation of x，y coordinate and distance to the Moon between Model 1 and Model 5

从图6～图9可以看出，曲线随着积分时间的推进逐渐发散，下面分别对以上积分的前1、2、3个月的均方差进行统计，统计结果如表2所示。

从表2可以看出，不考虑太阳引力的模型误差最大，量级为几千km，其次是不考虑太阳光压的模型，误差量级为几十到几百km，再次是不考虑月球非对称引力的模型，误差为1 km左右，最后为不考虑金星和木星引力的模型，误差量级不到1 km。在实际工程应用时，在一定精度要求下，一些次要的摄动因素可以忽略不计，本文提出了一种结构简单的高精度地月DRO动力学模型，下面就该模型的建立和精度进行分析。

对于地月DRO飞行器而言，地月会合坐标系相对地月惯性坐标系之间的旋转直接反映了太阳引力和月球轨道偏心率对其运行轨迹的影响。因此可以使用标准星历数据来表示太阳和月球的运动状态，获得星历模型下的拟周期DRO，从而实现在动力学模型中考虑太阳引力和月球轨道偏心率等摄动因素的目的。

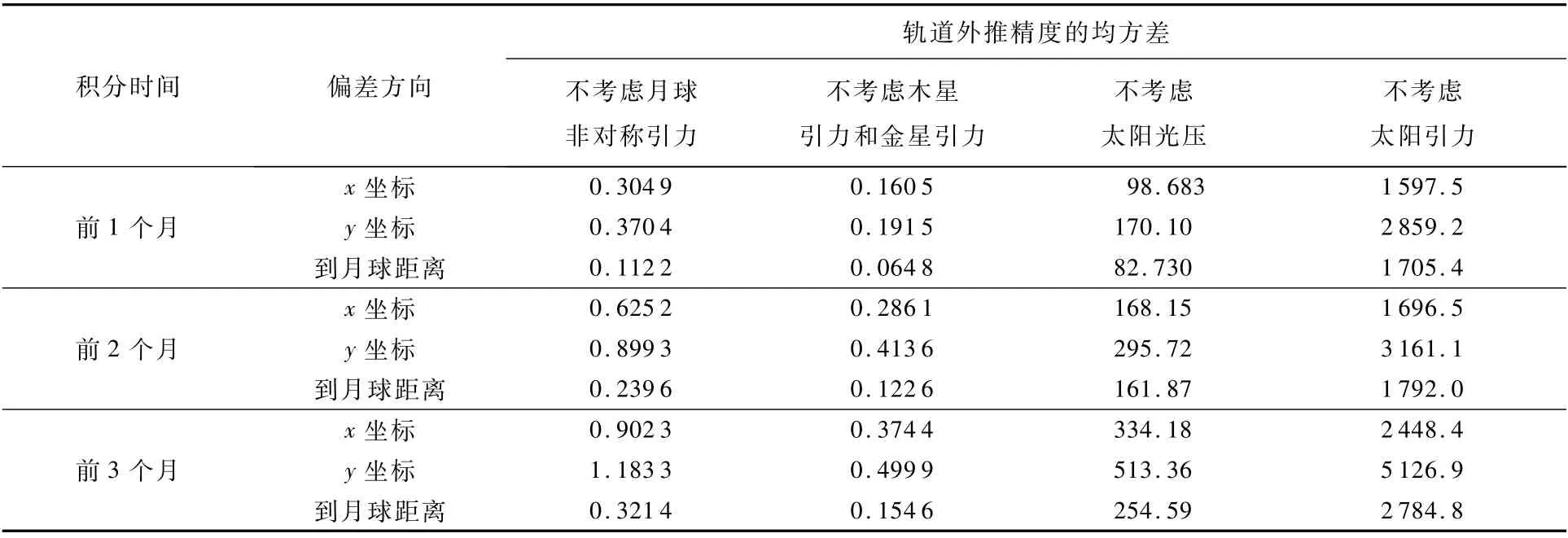
表2 不同摄动模型轨道外推精度的均方差统计结果Tab le 2 Statistical resu lts of m ean square error of trajectory extrapolation p recision for different pertu rbation m odels km

为了检验星历模型的精确性。本文在全力模型（考虑了月球轨道偏心率、太阳引力、金星引力、木星引力以及太阳光压5种摄动）和只考虑太阳引力和月球轨道偏心率的星历模型下对STK中的地月拟周期DRO初值进行了积分，积分器为龙格库塔7～8阶变步长积分器，行星星历表使用JPL的DE430。图10展示了全力模型和星历模型下，航天器坐标y、坐标x以及到月球距离在3个月积分时间内2种模型差值的均方差随时间的变化情况。

图10的仿真结果表明，在前10天的积分时间内，星历模型的误差在km量级，在前1个月的积分时间内，模型误差在几十km量级，随着积分时间的增加，模型误差逐渐增大。虽然在轨道外推时，模型误差很快达到km量级，但在地月系这样大尺度的空间范围内，仍然可以利用星历模型来分析DRO在实际力环境中的运动特性，为任务轨道设计提供理论依据。在工程实用中，导航测量弧段和轨道保持策略的确定要和模型精度统一进行闭环考虑。

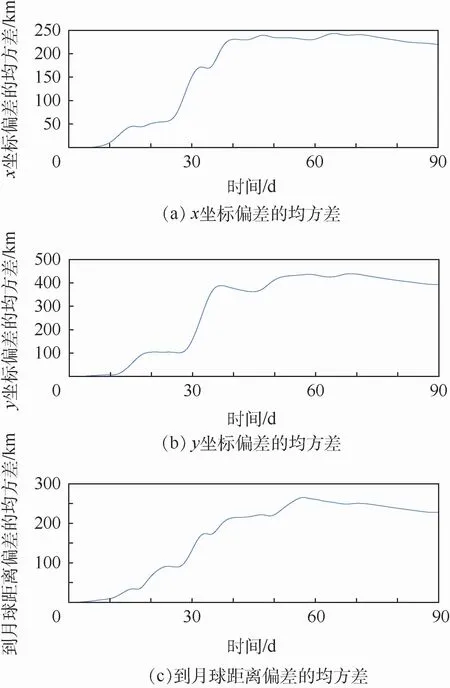
图10 星历模型和全力模型x、y坐标及到月球距离偏差的均方差Fig.10 Mean square error of deviation between ephemeris model and full forcemodel of x，y coordinate and distance to the Moon

4 结 论

通过流函数法在圆形限制性三体模型下求解得到DRO周期轨道族，并分析了轨道的非开普勒特性以及轨道形状在地月会合坐标系与地月惯性坐标系中随共振比的变化情况。其后分析了在摄动力模型下DRO航天器的运动特性以及影响DRO的主要摄动因素及其影响程度。仿真分析表明：

1）利用流函数法可以在近似解析解失效的更广大区域求取周期DRO的数值解。

2）整数共振比DRO（例如1∶2、1∶3、1∶4等）在地月惯性坐标系中是闭合的非开普勒周期轨道，而非整数共振比DRO在地月惯性坐标系中则是不闭合的，看起来像是在月球轨道附近打水漂。这是由于在CRTBP模型下，只有整数比的共振轨道航天器在地月惯性坐标系下与月球的相对位置变化呈周期性，即如果共振比为1 ∶n（n为正整数），DRO航天器在旋转系中逆行绕月n圈后，在地月惯性坐标系中与月球同时完成绕地球一圈，回到起点位置，从而在地月惯性坐标系中形成一条闭合的轨道。

3）摄动力模型下，DRO将演变为拟周期轨道，拟周期DRO仍可保持很好的稳定性，并且在地月系中，影响DRO轨道稳定性的主要摄动力是太阳引力，其次是太阳光压，接下来是金星、木星等行星引力摄动，分别比前几项摄动小3～5个数量级，在实际力模型中可以不予考虑。

4）在地月系中，只考虑太阳引力和月球轨道偏心率的星历模型能够近似地反映DRO在实际力模型中的运动状态，因此在实际工程轨道设计中可以使用星历模型来完成一些任务特性分析，为轨道设计奠定理论基础。

本文不同于以往的研究，针对深空导航和通信应用，得到了不同摄动项对DRO动力学模型精度的影响结果，提出了一种结构简单的高精度DRO动力学模型，可以用于高精度轨道方案设计，或者作为自主导航和轨道保持的在轨动力学使用。但是，本文最后建立的动力学模型没有计入太阳光压摄动，在后续的研究中有待进一步研究探讨，以提高模型的精度。