前测，对学生思维起点的了解更深入

李赛男

【摘   要】前测研究，可以有效地了解学生的思维起点，从而更精准地指导教学。通过对“圆柱的体积”教学前测研究发现：学生已具有的长方体体积和圆面积推导的知识基础和思想方法，對于学习圆柱体积公式的推导非常重要;无论是城市学校还是农村学校，教学中，教师都可以大胆放手让学生进行猜测，同时注重动态过程。

【关键词】圆柱的体积;前测研究;教学

课堂教学中，大部分教师会根据自己的教学经验来判断学生的思维起点，笔者通过前测了解学生的思维起点，从而更精准地指导教学。现将“圆柱的体积”教学前测研究过程与结果分析如下。

一、研究思路

在教学“圆柱的体积”之前，有多少学生已经知道了圆柱的体积公式？怎么知道的？如果是猜测的，思路是怎样的？思路合理的学生，基础是什么？这基础与他的猜测之间又有什么关系？根据这些问题，笔者设计了以下前测题：

题1：请你猜测圆柱的体积与什么因素有关？计算公式是什么？你是怎么知道的？

题2：请你解释为什么可以这样计算圆柱的体积？

前测对象为六年级学生，分别从本地区（使用北师大版教材）抽取4所学校，其中市级普通学校2个班级，镇级中心学校2个班级，村级完小3个班级，共291人。

二、前测结果及分析

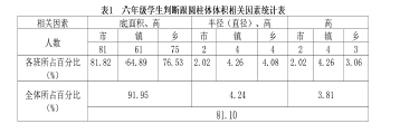
（一）约有81.10%的学生知道圆柱体积公式

根据题1的调查结果统计发现，已经知道圆柱体积公式的学生约占总人数的81.10%。在这些学生当中，认为圆柱体体积只与高这个单一因素有关的学生占知道人数的3.81%。认为与半径（直径）、高有关的占知道人数的4.24%，而认为与底面积、高有关的占知道人数的91.95%（见表1）。

通过分析，笔者发现：

1.超过80%的学生知道决定圆柱体积的是底面积和高（猜测半径的学生也是理解的，因为圆柱体底面是圆，圆的大小由半径决定），对于六年级的学生来说，平面图形面积和体积的学习中都有涉及高，使得他们直觉上判断与高有关。

2.城乡之间差异不明显。镇和乡这两级当中，乡校不一定比镇校弱，相反有些数据乡校还比镇校高，根据笔者的经验判断这与上课教师有关。

（二）约有20%的学生不知道圆柱体积公式

大约有20%的学生不知道圆柱体体积公式，由访谈可知，学生不知道的原因主要有以下两点：

1.圆柱体体积涉及底面积的大小和高，部分学生对体的三个维度不明确，从而不能从长方体体积以及长、宽、高三个维度把握体积的概念。

2.因为学生对体积概念的感知以及对长方体体积的知识没有产生迁移，从而不知道从哪入手。

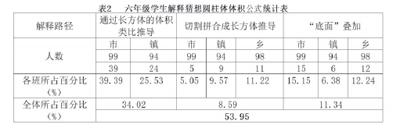
（三）约有53.95%的学生能分别采用三种解释路径

通过对题2的调查结果统计发现，能对猜测的公式进行合理性解释的学生约占总人数的53.95%。他们分别用了三种解释路径（见表2）。

解释路径一：通过长方体体积类比推导，如学生1认为长方体和圆柱体差不多，并用阴影表示了底面积（图1）。

解释路径二：通过“底面”叠加推导，如学生2很好地解释了叠硬币形成圆柱的过程（图2），“许多个”累积成了一定的“厚度”，就形成了高，此路径可以动态演示。

解释路径三：通过切割拼合成长方体推导，如学生3所做的解释（图3）。

（四）学生回答水平层次分布情况分析

从学生的回答来看，他们所处的水平层次和认知能力是不同的。

笔者参照SOLO分类理论，按照圆柱的体积相关因素典型回答，将水平层次及评价标准确定如下：

水平0：做错了或没有做的，这类学生有55人，所占的比例是18.90%。

水平1：只找到单一的信息，能猜测到圆柱体体积的相关因素，但不能猜测出公式，无解释，这类学生有19人，所占的比例是6.53%。

水平2：学生能注意到多个信息，如学生4（图4）不仅回答出圆柱体积的相关因素是底面积和高，还能写出体积公式，但是无解释或解释错误。这类学生有60人，所占的比例是20.62%。

水平3：学生能注意到许多相关信息和线索：能猜测出相关因素是底面积和高;能够准确写出公式;能够在知识维度或方法维度解释体积公式的合理性，将体积公式的推导与以前的知识比如长方体体积进行类比。这类学生有99人，所占的比例是34.02%。

水平4：学生能够猜测出相关因素是底面积和高;能够准确写出体积公式;能够进行合理解释;还能够与长方体进行类比，甚至能与求圆的面积的知识进行类比，把圆柱平均分成若干份，拼成近似的长方体，从方法维度和知识维度综合推理解释，以现有的知识结构，有适当思维拓展（图5）。这类学生有58人，所占的比例是19.93%。

笔者翻阅了现行的五套国内教材，发现教材都有回顾求圆面积和长方体体积公式的推导，这是从知识维度、方法维度回顾的。学生对于这两部分内容的回顾情况如何呢？

（五）圆面积公式和长方体体积公式回忆情况分析

是不是圆面积公式和长方体体积公式知道，推导过程也很清楚的学生，处于水平3和水平4？需要继续测试，笔者设计了以下前测题。

题3：圆面积公式是什么？请你回忆是怎样推导圆面积公式的？（借助画图、文字说明）

题4：长方体的体积公式是什么？请你回忆一下我们是怎样推导长方体体积公式的？（借助画图、文字说明）

1.约有63.23%的学生能回忆圆面积公式的四种推导过程（见表3）。

通过统计发现，63.23%的学生已经理解了圆面积公式的推导路径，有一定的转化思想基础，并且出现了多种转化方式。36.77%的学生不能正确回忆，可能是新课学习时候就没有理解，或者出现遗忘（前测和学生学习圆面积时大概中间隔了五个月）。

2.约有29.55%的学生能回忆长方体体积公式推导过程（见表4）。

从学生的问卷看，有205名学生只记得公式，不知道推导方法。选了其中的6位学生进行访谈，5位学生给予提示可以回忆，1位回忆不了，说明这部分内容学生遗忘得比较多，或者学的时候就没理解，处于死记硬背的状态。

进一步分析发现，知道圆面积公式推导和长方体体积公式推导方式的学生有86人，这当中有多少学生知道圆柱体体积公式并能进行合理的解释呢？75人，占知道圆面积公式推导和长方体体积公式推导方式学生的87.21%。

三、前测结论

基于以上前测与分析，“圆柱的体积”学习前学生的情况如下：

1.有约80%的学生，教学前就已经知道圆柱体体积计算公式。

2.猜测圆柱体体积跟高有关的学生人数超过80%。

3.有53.95%的学生对于圆柱体体积公式的解释能达到較高水平3和水平4，不仅能解释体积公式的猜想，还能够将体积公式的推导与以前的知识比如长方体等结合在一起，并且适当拓展。

4.学生关于圆的面积公式和长方体的体积公式的推导掌握程度直接影响对圆柱体体积公式的猜想。

四、教学启示

基于以上分析，得到以下三点教学启示。

1.无论城市还是农村，教学实践时，教师都可以大胆先让学生去猜测，再动手操作去验证。

2.学生已具有的长方体体积和圆面积推导的知识基础和思想方法，对于圆柱体体积公式的推导非常重要。所以，教学长方体体积公式推导的时候不仅要强调长乘宽乘高，而且还要强调底面积乘高，这是柱体普遍的公式，带有一般性，对推导圆柱体体积有作用。

3.在圆柱的认识时，让学生感受到圆柱可以看成是“由很薄的圆面叠加得到”，会有利于学生直观解释圆柱体的体积公式。

（本文在研究过程中，得到了朱乐平老师的多次悉心指导，在此，表示衷心感谢！）

参考文献：

[1]吴玉兰，等.圆柱与圆锥的认识、表面积和体积教学研究[M].北京：教育科学出版社，2014.

[2]John B.Biggs，等，著.学习质量评价：SOLO分类理论[M].高凌飚，等，译.北京：人民教育出版社，2010.

（浙江省东阳市画水镇陆宅小学   322102）