借助多元表征从“操作”走向“理解”
———《搭配》教学
周兴蓉,张麟
【教学内容】
浙教版二年级上册第88、89 页。
【教学过程】
一、导入新课,激发兴趣
师:同学们,我们每天都要与吃、穿、行打交道,这些事情中有什么数学问题呢?
生:各种菜要搭配着吃。
生:还有搭配穿衣服。
师:是呀,这些事情当中就有搭配的数学问题,今天就来研究有关搭配的知识吧。(板书课题)
【设计意图:以学生耳熟能详的生活情境导入,让学生感受到数学就在生活中,从而激发他们探究数学问题的兴趣。】
二、创设情境,探究新知
师:老师准备了三件上衣和两条裙子,你打算怎样搭配?一共有几种不同的穿法?(课件出示)
活动要求:
1.拿出衣服卡片摆一摆,并记录下你摆了几种。
2.同桌交流,把自己记录的方法介绍给同桌。
(学生操作时,教师巡视,引导学困生。同桌交流后进行汇报)
生:第一件衣服和第一条裙子、第一件衣服和第二条裙子、第二件衣服和第一条裙子、第二件衣服和第二条裙子、第三件衣服和第一条裙子、第三件衣服和第二条裙子,一共有6 种。
生:他那种有些麻烦,我是这样,衣服1 和裙子1、衣服1和裙子2、衣服2 和裙子1、衣服2 和裙子2、衣服3 和裙子1、衣服3 和裙子2,也是6 种。
生:我还有更简便的,给它们编上号,①~⑤号。
师:编号的方法很好,谁能在她的基础上再改进一下?
生:上衣、裙子是两类东西,要分类标号。那裙子就用字母a和b 来表示吧。
师:这样搭配出来会怎样呢?
生:就是①a、①b、②a、②b、③a、③b 也是6 种。
师:非常清楚明了,还有不同的表示吗?
生:我还有不同的,连线,很方便快捷,也是6 种。
师:你能介绍一下是怎么连线的吗?(学生说,教师课件演示,如下图)

生:我用△表示上衣,□表示裤子。也可以把它们连起来。
师:真不错。刚才这么多方法都找出了6 种,有什么相同和不同的地方吗?
生:表示的方式不同,但结果都是相同的,都有顺序。
师:如何能做到有序呢?
生:就是要做到不漏掉,也不重复。
师:说得真好,刚才的那些好方法就是做到了不重不漏。
【设计意图:通过学生实际摆、充分说,以“摆”来帮助思,以“说”来表达理,在“摆”中发现问题,在“说”中解决问题。充分利用学生原有的差异,借助学生间互相交流,感受符号化表示的简洁高效。利用多元表征让学生感受到无论用什么方式进行表示,目的都是为了有序地进行思考。】
师:你们会把连线的方法用算式表示出来吗?
生:3+3=6(种)。
师:你是怎么想的?
生:1 条裙子搭配3 件上衣,2条裙子就有2 个3,所以3+3=6。
师:还可以列什么算式呢?
生:2+2+2=6(种)。1 件上衣搭配2 条裙子,有2 种,3 件上衣就有3 个2,所以2+2+2=6。
师:刚才列的都是加法算式,还可列?
生:乘法算式,2×3=6(种)或者3×2=6(种)。
师:为什么可以这样列?
生:2 个3、3 个2 都可以用乘法2×3 或3×2 来表示。
师:分析得真好。如果增加1条裙子,一共有几种搭配方法?
生:因为有3 件上衣,增加1条裙子就增加1 个3,共有3 个3,3×3=9(种)。
师:如果增加1 件上衣,一共有几种搭配方法?
生:有2 条裙子,增加1 件上衣就增加1 个2,共有4 个2,4×2=8(种)。
【设计意图:通过观察有序的连线图,学生从形得到数,再从数得到算式,从而理解考虑搭配的所有方法就是思考有几个几。通过变化某个搭配要素的数量,从而观察增加的是几个几,进一步加深对搭配问题的理解。】
三、联系生活,解决问题
1.乒乓球比赛中的数学问题。
师:4 位学生和2 位教师进行乒乓球单打比赛。如果每位学生和每位教师都打一局,一共要打多少局?
生:2×4=8(局)。从教师出发,每位教师与4 位学生都要打一局,就是2 个4;如果从学生出发,每位学生都要与2 位教师打一局,就是4 个2。都能用2×4 来表示。
课件出示连线图。(如下图)

2.走路中的数学问题。
师:聪聪家到少年宫要经过学校,从家到学校有3 条路可走,学校到少年宫有2 条路可走。一共有几种走法呢?
生:3+2=5(种)。
生:应该是3×2=6(种)。
师:你们觉得哪一种是对的呢?为什么呢?谁能解释呢?
生:我认为3×2=6 是对的。因为聪聪家到学校有3 条路可以选,学校到少年宫有2 条路可以选,所以是3×2=6。
生:用符号①、②、③分别表示聪聪家到学校的线路,用a、b来表示学校到少年宫的两条线路。连一下线,就是有6 种选择。
生:选了一条聪聪家到学校的路后,后面从学校到少年宫就有2 条路可选,这样就有3 个2,所以是6 种。
师:分析得都很好,这题与之前的搭配题目有什么联系呢?
生:家到学校有几条路相当于上衣有几件,从学校到少年宫有几条路相当于裙子有几条。其实是一样的,就是换了种形式。
【设计意图:通过研究生活中常见的两个情境,进一步加深对搭配问题的理解。乒乓球比赛的情境变化了搭配要素的数量,进一步理解几个几的含义。路线的情境将搭配的要素隐藏在题目信息中,需要学生深入思考判断,并感受与之前的搭配问题的联系,从而让理解更加深入。】
四、联系实际,拓展巩固
师:体育器材室有以下三种球各若干个,可以任意拿两个,有多少种选择?分别是什么?

生:有3 种,分别是橄榄球和篮球、橄榄球和足球、篮球和足球。
师:有不同的想法吗?
生:我认为是6 种,因为这里说可以任意拿两个,那么拿两个篮球也是可以的。刚才3 种是两次拿球不一样的,还有3 种是两次拿球一样的。
师:可以拿两个同样的吗?
生:可以,题目说任意拿两个。
师:大家再思考一下,应该怎么想呢?可以在活动纸上试一试。
(学生操作,教师巡视,了解学生的掌握情况,适时引导帮助)
分享学生成果(如下图),得出:3+2+1=6(种)或3+3=6(种)。
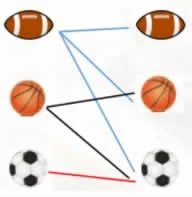
师:什么情况下只有3 种呢?
生:如果规定不能拿相同的球的时候就只有3 种。
师:嗯,分析得很好,看来看清题意非常重要。
师:这节课大家有什么收获?
【设计意图:用学生身边熟悉的情境改编为变式练习,试图打破学生用两种搭配要素的数量相乘得出搭配总数的思维定势,避免学生出现单一的模式化思考。从而进一步促进学生理解搭配问题的本质,用合理的方式不重不漏地思考出所有的可能。】

