开放性练习,尝试用数学语言表达
孙贵合
在前两篇文章中(分别于本刊2020 年第1-2 期、第3 期所刊登),我们谈到了应用开放性练习使学生能够用数学的头脑思考世界、用数学的眼光看世界,而如何能够让学生用数学的语言表达世界,则是课堂教学中的重要任务。本节我们围绕这一主题和大家进行交流。
那么,什么是数学语言呢?数学语言可分为抽象性数学语言和直观性数学语言,包括数学概念、术语、符号、图形等。可以归结为文字语言、符号语言、图形语言三类。数学语言作为数学理论的基本构成成分,具有“高度的抽象性、严密的逻辑性、应用的广泛性”。简单而言,数学语言科学、简洁、通用。
在课堂教学中,师生之间的交流、生生之间的交流、学生自己的独立思考等,随时都在发生。但我们在听课和上课过程中发现,学生在表达自己意见时说不到位、说不清楚的现象非常明显,这是为什么呢?明明学生已经理解了,可为什么表达起来还是费劲呢?数学语言的表达应该是简单、明了的,不分国界的,世界通用的。而且能够用数学语言表达,学生学习起来也应该是轻松的,为什么我们学生的学习会越来越累呢?
究其主要原因是在课堂教学中,教师对于如何用数学语言表达,没有或很少带领学生学习和体验过。
案例一:《“1”》。
画图法,是数学语言表达的一种重要形式。画图法能够帮助学生理解数量关系、理清算法,同时也是学生思维过程的一个外显。所以学生在解决实际问题时,能够画出图是很重要的一种数学表达。特别是高年级的教师经常会遇到这样的情况:当学生解决问题时遇到困难了,教师会说“你回去自己画画图”。可是会发现一个奇怪的现象:会列式的学生会画图,不会做的学生也不会画图。为什么会出现这样的情况呢?那我们应该反思教学,在小学六年的教学中,有哪一课安排了学生学习如何画线段图呢?答案是没有。我们在课堂教学中,无数次的使用线段图,但看明白了就能画出来吗?我想是不一定的。
针对这种想法,在人教版三年级上册《归一问题》一课教学中,学生第一次接触线段图时,除了让学生学习“归一问题”之外,更重要的是让学生通过“归一问题”来学习画线段图。
环节一:
师:同学们,你们喜欢美术课还是数学课?我们今天上数学课,但数学课里面也有画,不过和美术课的画不一样。数学课上的画是看谁画得简单,而且一眼就能够看明白。

师:这句话能看明白吗?能说明白吗?那你们能画明白吗?
(学生尝试画。教师巡视发现有的学生在画小人,有的学生在画商店等等,并不是数学的画)
师:同学们想一想,我们数学的画,重要的是哪两点?
生:简单还能让人一眼就看明白。
师:可有的同学还在画小人、商店,你们有没有简单的画法?
生:可以用文字或图形。
师:我们一起来欣赏这位同学的作品。你们能看明白吗?
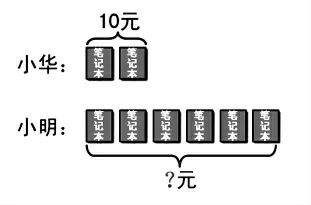
生:明白了,它的一个长方形就表示一个笔记本。
师:他是用长方形表示的练习本,还可以用什么表示?
生:圆形、三角形、小竖线、小横线……
师:对,这些表达方法都很简单,数学上一般用小横线来表示,我们一起看看这位同学的作品,你们能明白是什么意思吗?
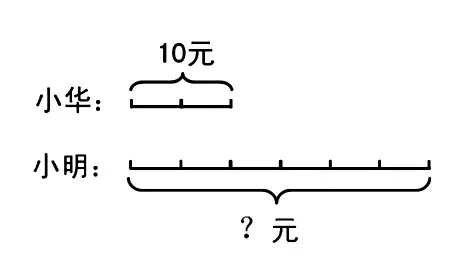
生:一个小横线就表示一个笔记本。
师:我们用这样的图表示,是不是看起来更清楚?那你能根据文字表达结合我们画的图来列出算式并解答吗?
本环节的设计,首先,在学生初次接触线段图时让学生感受线段图是怎样产生的。即用图去描述问题中所表达的情境,选择重要的信息表示在图上,从而让学生对画线段图减少心理恐惧,为自己能够画出线段图做好心理铺垫。其次,通过学生用自己创造性的表达,逐步抽象出线段图的过程,使学生明白:线段图只是一种表达形式,比长方形、圆形等表达起来更简洁,从而真正理解线段图的作用。第三,让学生感受画线段图并不难,只是把数学信息依次用图形表示出来,也就是如何画线段图。经历这样的体验过程,学生才能够真正从心理上、知识体系上、方法上掌握画线段图。
环节二:
师:同学们,你们还有其他方法解决这个问题吗?
生:6÷2=3,3×10=30(元)。
师:你们明白他的意思吗?
生:不明白。
师:看来用语言解释起来很麻烦,而且大家还不了解,那是不是可以考虑让线段图来帮一下我们呢?
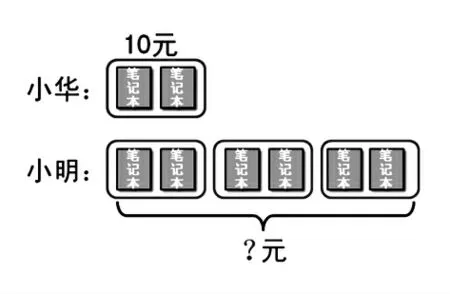

生:我明白了,就是把两本算成一份,看小明有这样的几份。
师:那刚才你们不明白,现在明白了,应该感谢谁?
生:线段图。
师:想对线段图说点什么?
生:线段图谢谢你,你帮我理解了原来我不理解的知识。
本环节的设计,是进一步突出线段图的作用,从而让学生从心理上接受线段图。当学生用语言描述、分析、理解不清时,线段图的作用突显出来,让学生真正感受到线段图能够帮助理解、分析和思考。当感受到价值时,学生才能够真正地接受线段图,并愿意去学、去尝试、去运用。从而慢慢学会用线段图这种数学语言去表达。
案例二:《三角形边的关系》。
“语言表达是思维的外壳”。学生能够用数学的语言表达,就一定要有数学的思考。数学思维就是用数学思考问题和解决问题的思维活动形式。而“推理”又是数学思考中很重要的一种方法。在小学阶段多以归纳推理为主,而到初中以后,才会慢慢接触到演绎推理,在小学课程中,我们是否可以考虑让学生体验演绎推理的方法。让这种“因为……所以……”“由于……因而……”“因此”“之所以……是因为……”等词语出现在课堂中。词语只是表面,更重要的是让学生有数学的思考。
在学习《三角形边的关系》一课后,我出了这样一道开放性练习:你能用今天所学习的知识,证明梯形的a、b、c 三条边的和大于d 边吗?

你能证明a+b+c>d 吗?

你能证明a+b+c>d 吗?
当看到这个问题时,学生很茫然,一种无从下手的感觉。在小学阶段的学习中,学生没有经历过完整的证明过程,所以更有必要在简单的问题上让学生经历、体验一次,从而积累他们的学习经验。当加入e 这条辅助线时,学生立刻明白了,并且能够用完整的语言来表达。
生:因为b+c>e,a+e>d,b+c已经比e 大了,所以a 再加上一个更大的数就比d 更大了,所以a+b+c>d。
通过这样一道简单的练习题,在巩固本节课知识的同时,又让学生感受到除了观察之外,更严谨的证明方法,同时这样数学的表达是课堂中最需要的,也是学生后续发展的动力与源泉。可见在课堂中,适当为学生提供演绎推理的机会,为学生能够用数学的语言去表达起到了很大的作用。
综上,学生在课堂中不会用数学语言去表达,更多的原因在于教师没有能够给学生机会去体验、去学习、去感悟。当然除了上面所列举的用线段图表达、演绎推理的语言表达之外,还有很多方面,包括数学的概念名称等。如学生已经学习了奇数、偶数,但还在用单数、双数去表达,这时教师应该有意识地进行提示,让学生慢慢学会用标准的语言表达。数学公式的精准表达、概念定义的严密等多方面,让学生在不断运用的过程中,逐步感受到数学语言表达的科学性、简洁性与广泛性,从而慢慢喜欢上数学表达。这是一个漫长的过程,但只要教师在每一节课中都给学生机会,学生一定会喜欢上数学表达,更进一步爱上数学。

