四足机器人步态规划研究

付 晶， 党宏社， 王亚波， 刘丽萍， 茹 锋， 王 萍

(1.陕西科技大学 电气与控制工程学院， 陕西 西安 710021; 2.长安大学 电子与控制工程学院， 陕西 西安 710064)

0 引言

在山地、台阶、泥淖等地形复杂的环境，尤其是在执行危险任务的过程中，四足机器人得到越来越多的重视及应用.各国陆续开展了四足机器人深入研究，例如美国波士顿动力公司相继推出的BigDog、Wild Cat、Spot[1]四足机器人.2011年，我国863计划启动“高性能四足仿生机器人”主题项目，以期突破仿生柔顺机构、移动感知能力、平衡性和动态运动能力等核心技术，使我国四足仿生机器人实现跨越式发展[2].

仿生机器人在结构和运动模式上模拟生物，走在机器人前沿的Big Dog[3-5]就是仿生机器人的代表，它可在崎岖的地面上以稳定的步态运动,足端轨迹也多种多样.马宗利等[6]在仿猎豹四足机器人设计了一种液压驱动的柔性脊椎和腿结构.马慧姝等[7]设计的电驱四足仿生机器人实物本体,借鉴仿生学思想,提出一种基于哺乳动物运动轨迹的仿生步态策略来规划四足机器人足端轨迹.李志[8]结合正弦轨迹与椭圆轨迹规划出类椭圆轨迹.郭晖晖[9]设计了一种关节角度跟踪的闭环反馈控制算法，可以保证四足机器人的稳定行走.王玉闯[10]利用ADAMS对四足机器人进行walk和trot步态的仿真与分析.蒋建新[11]对四足机器人的运动学和动力学进行研究与分析，并简化了机器人的运动控制复杂度.王立鹏[12]在足端轨迹规划的基础上研究了四足机器人.目前，国内从事仿生机器人研究的机构很多，针对四足步态轨迹规划的仿真仍存在很多研究空白.

本文首先讨论仿生四足动物行走机理和运动学分析，然后运用ADAMS和MATLAB联合仿真系统验证所规划的仿生步态，最后构建实体四足机器人系统验证行走步态，取得了较好的效果.

1 仿生四足哺乳动物的行走机理和运动学分析

1.1 仿真样机简介

以马为例，马的腿部涵盖了髋、膝、踝、趾骨关节，共包含4个自由度.其行走主要依靠髋关节的摆动，膝关节保证在前进中足部不触地，而踝关节和趾骨关节则是在接地时缓冲瞬时压力并储存部分能量，并且在抬腿时完成能量释放，调整俯仰角度.腿部从髓关节向下，主动自由度降低，被动自由度增多，这也与其步行中的能量转换关系是相互对应的，对于四足机器人的步态规划具有借鉴价值.

如图1所示，为马的四种常见步态.步行步态是一个四阶段的过程，见图1(a)，每次一条腿作摆动足迈出，按左前腿lf、右后腿rb、右前腿rf、左后腿lb的步态时序，其重心处于支撑腿搭建的三角形稳定范围内，实现前进的稳定性.行进速度相对更快的是小跑步态(见图1(b))和疾驰步态(见图1(c)).它们的步态占空比都是0.5.它们的共同之处在于，同在摆动相和支撑相的腿一并起落，马用两条腿触地支持，另外两条腿腾空向前迈出.图1(d)是溜蹄步态，略快于步行步态.

(a)行走

(b)小跑

(c)疾驰

(d)溜蹄图1 马的四种常见步态

1.2 运动学分析

依照马的运动特点，建立机器人模型，如图2所示.整体结构由躯干、左前腿、右前腿、左后腿、右后腿五个部件构成，大腿及小腿的长度分别为l1和l2,机器人腿部包含两个自由度，分别为θ1和θ2.

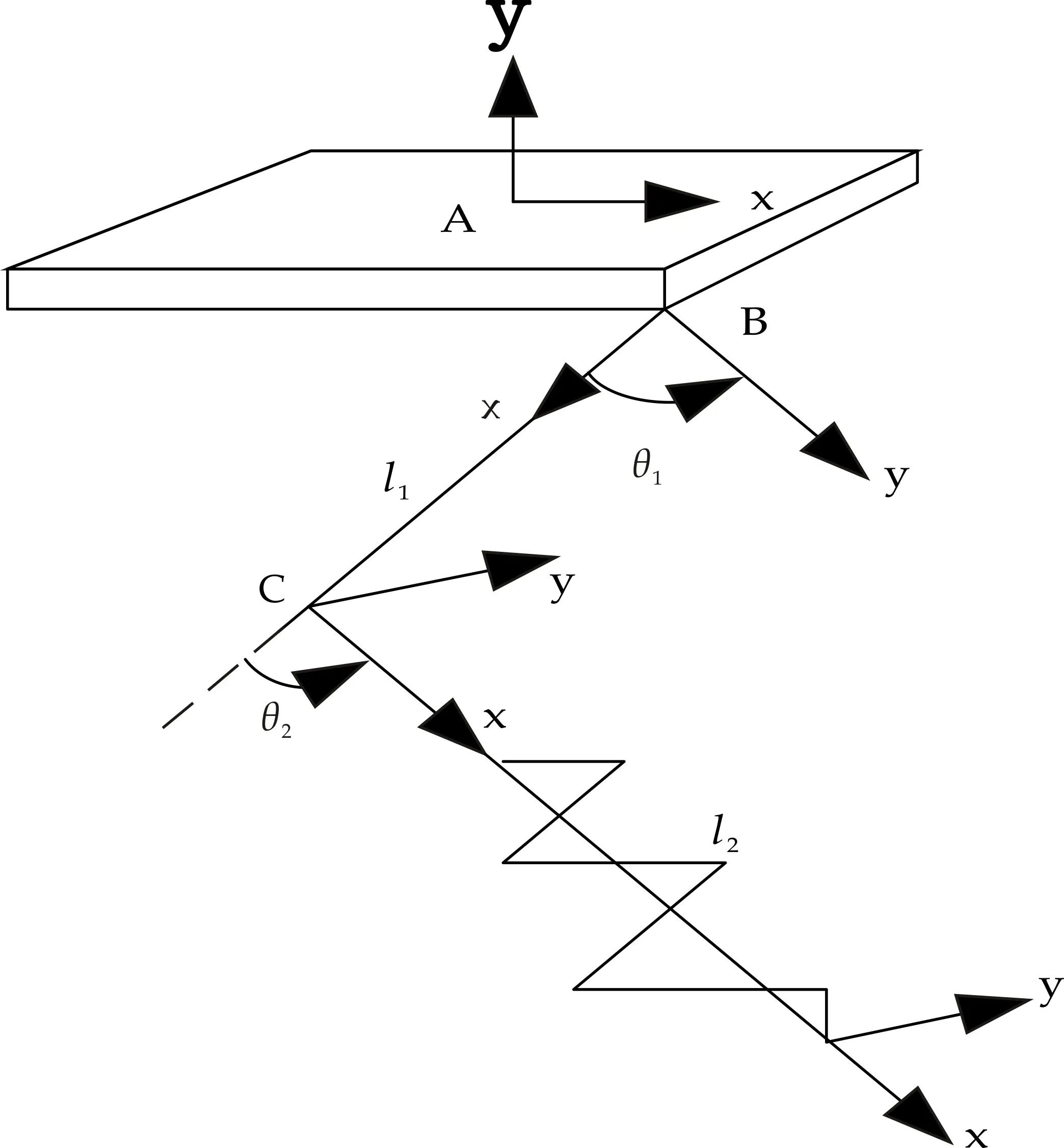
图2 机器人模型

建立步态参数，如图3所示.步态周期为T，运动占空比为β，速度为v，步长为s,脚尖离开地面的竖直高度为h，髋关节角度为θh，髋关节角度摆动相的稳定足部转角位为θh0、θk0.

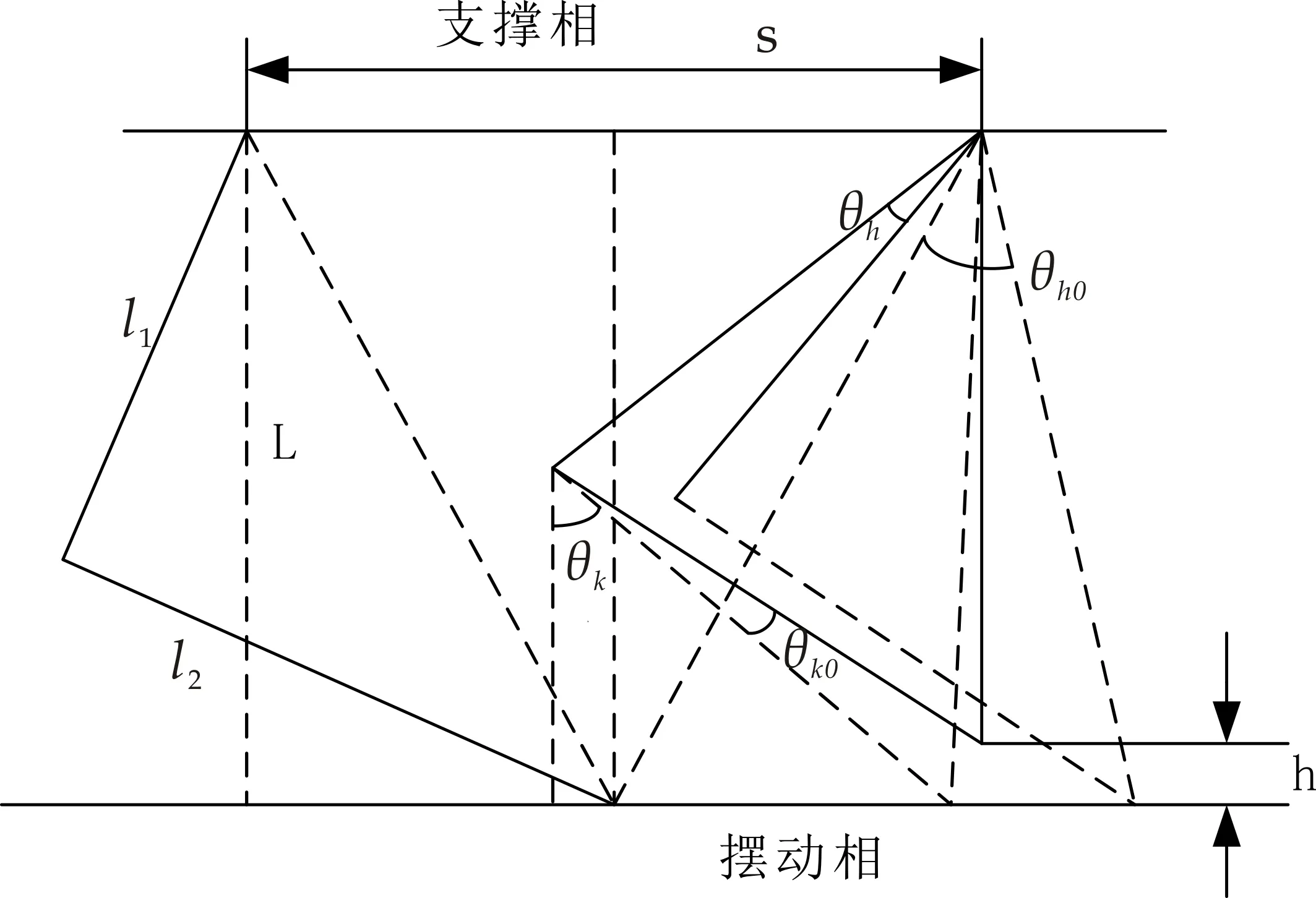
图3 机器人步态参数

根据图中运动和几何关系可知

(1)

S=vTβ

(2)

L=(l1+l2)cosθh0

(3)

求解髋关节摆动角度为

(4)

由图可以推导膝关节转动角度为

(5)

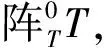
(6)

而其中，

(7)

(8)

(9)

求解得

(10)

则足部的位置坐标方程为

(11)

已知机器人足部相对于标准坐标系的位置和姿态，根据前一步的数据计算出由逆运动学可得θ1和θ2的值，也就是逆运动学求解，得：

(12)

(13)

2 基于ADAMS与MATLAB的仿真

2.1 仿真流程

本文采用两种仿真实验方案.第一种方案是应用ADAMS绘图，在其运动学分析功能下进行步态的数据测算，记录有效的部分；第二种方案是利用MATLAB与ADAMS进行联合调试，可以监测样机行进中的运动参数，进而编辑控制函数，满足调整机器人的位置与姿态的要求.仿真流程图如图4所示.

图4 仿真流程图

2.2 机器人仿真实验

本文将采取多个方案进行对照实验，分别为平面测试、斜面测试及步行步态和溜蹄步态的探索实验.

2.2.1 平面实验

平面实验中，以小跑步态为对象,对角上的两条腿同时运动，机器人身体稳定性较好.由图5可以看出，没有在横向发生较大的位移，整体效果达到预期要求.

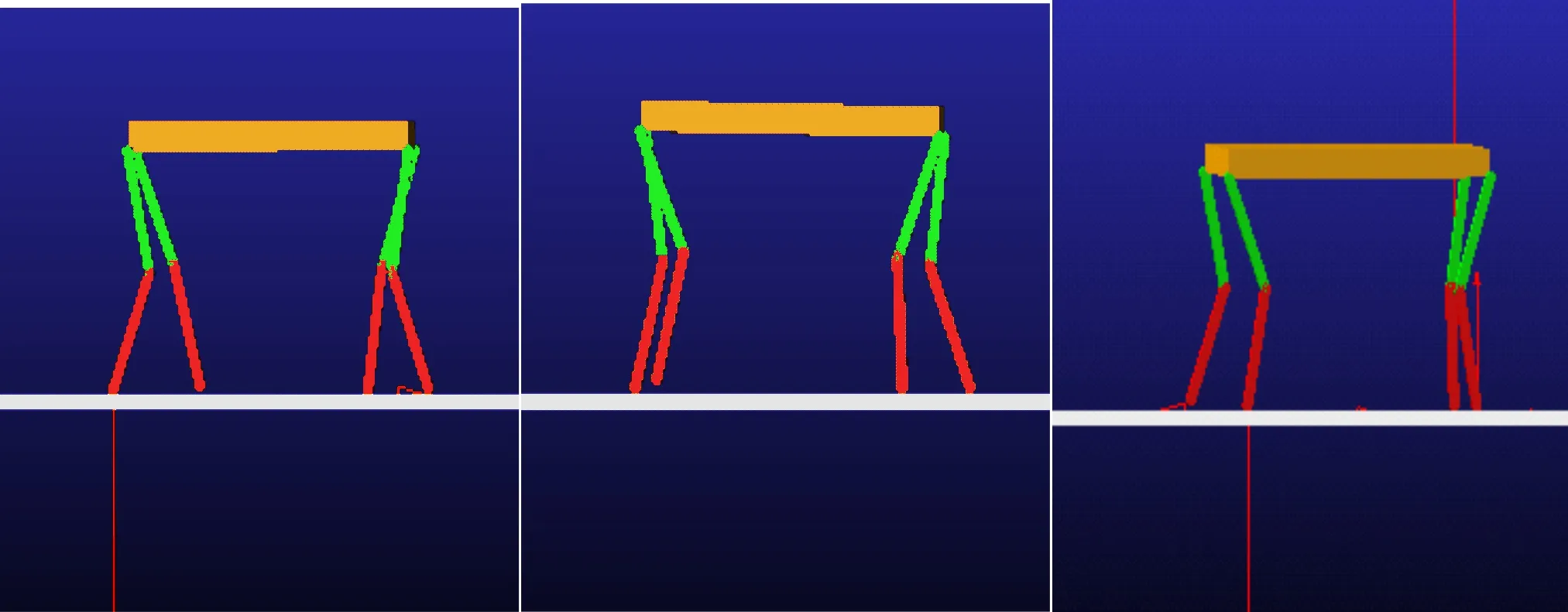
图5 机器人的小跑步态实验截图

测量机器人的关节曲线如图6所示.红色曲线为髋关节驱动函数，蓝色为膝关节驱动函数.右前腿的髋关节驱动可等效为正弦函数，在正半周期内，膝关节完成摆动动作，其中小腿先以顺时针方向旋转至最大角度，此时髋关节同时达到顺时针旋转的最大值；然后，膝关节逆时针旋转，小腿开始伸展直至最大值，髋关节也摆动到最大值；在负半周期内，髋关节完成逆时针运动，带动腿部蹬地向前行进.一条腿的运动周期为1 s，图6中0.25 s至1.25 s是一个完整的周期.

图6 髋关节和膝关节的驱动函数

图7是左前腿和右前腿的髋关节驱动函数，相位差为半个运动周期.这也表示不同侧的腿是交替运动的，髋关节角度是驱动行进的主要参数.

图7 前腿髋关节的驱动曲线

由表1可看出，X轴的速度值始终为负值，表明前进的方向为X轴负半轴，竖直方向的几个尖峰表示行进中有颠簸，整体起伏不大，说明未发生较大位移.

2.2.2 斜面实验

在机器人斜面实验截图中，由图8可知，机器人有离地情况，运行状况较为稳定.

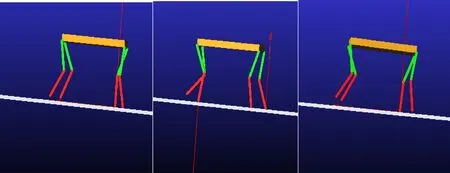
图8 机器人斜面实验截图

表1中前进方向的曲线，显示机器人在7 s内X轴位移约是1 700 mm，运行较快.竖直方向Y轴的曲线表明模型在行进中的起伏，较为稳定，Z轴曲线则表明行进中略有偏移的倾向，但从整体上来看，步态质量尚算稳定.

需要注意的是，地面的倾斜角度不能旋转得到，而是调整地面的起始坐标实现.另外，需要调整足端与地面的摩擦因数和切入深度，获得足够的驱动力量.由于反作用力，行进时会有双腿离地的情况.因为受力的原因，前进方向上会有静止的时刻，竖直方向的起伏幅度较大.横向位移起初有较大的波动，随着时间推移，渐趋平缓.通过ADAMS可以绘制足端轨迹.

如图9所示，在X-Y平面曲线大致为锯齿形，这就可以很好地适应倾角路面，而在X-Z平面的曲线表明，机器人在横向有一定的偏移，驱动函数需要做出调整.

(a)轨迹正视图

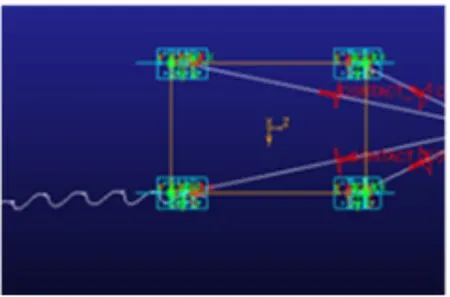
(b)轨迹俯视图图9 足部轨迹的绘制图

表1 仿真实验截图与曲线

2.2.3 溜蹄步态实验

根据溜蹄的步态运动截图，从图10可以观察到，机器人的运动起伏很大，且存在四足悬空的情况，这与之前分析的动物步态相符合.

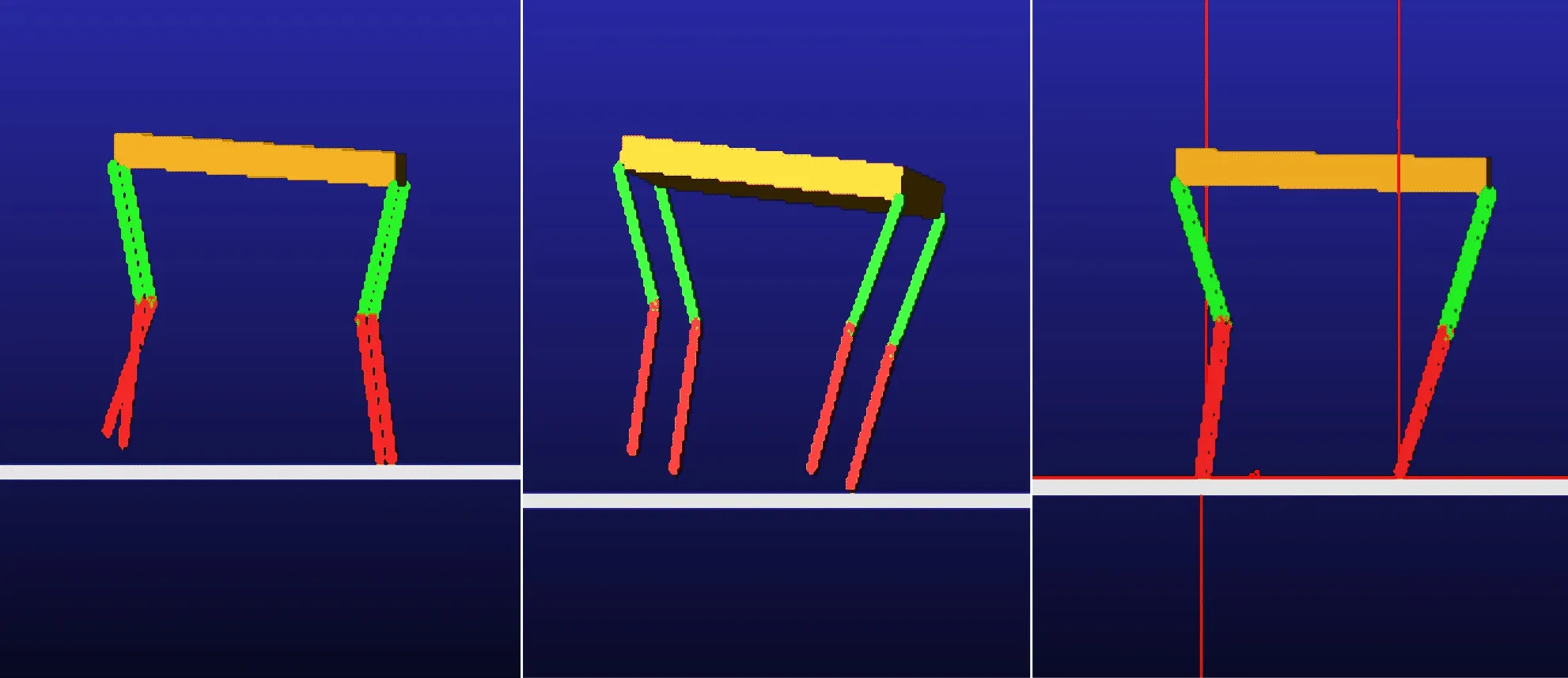
图10 机器人gallop步态实验截图

根据表1中实验测得数据可知，模型在7 s内的位移约为2 700 mm，这显然快于小跑的运动姿态.质心在竖直方向的起伏不大，约为30 mm，不过从运动视频分析，俯仰角的变化很大，说明这种运动姿态减少了竖直方向的做功，减少了运动中的身体能量消耗.

2.2.4 行走步态仿真

与小跑步态类似，图11中步行的行进姿态也是速度较慢的运动，每次有两只或三只足撑地.

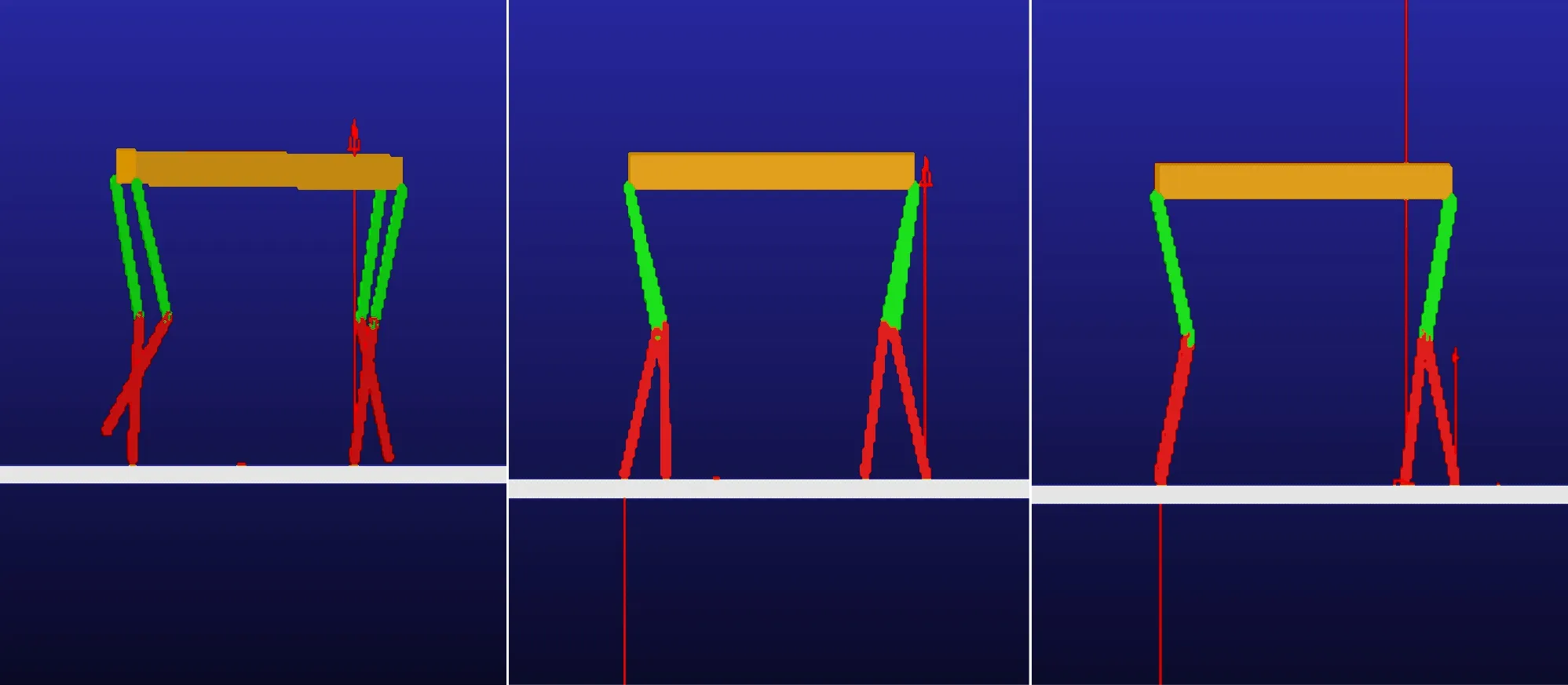
图11 机器人walk步态实验截图

由表1可知，7 s的位移大约为800 mm，这稍慢于小跑的情况.竖直方向起伏较小，稳定性最佳.不足之处在于，且横向的起始位移较大，约为120 mm，后面仍有偏离主线的趋势.

3 四足机器人步行实验

3.1 硬件系统设计

机器人采用内膝肘式配置，这种配置可以减少能量的消耗[13].驱动装置是机器人步态规划中的关键内容，液压装置使用高压油作传动介质，它的驱动力矩大，运行稳定，但驱动装置的构造繁琐，适合大型步行机.电机驱动控制灵活，驱动精准，花费较少，满足小型机器人的传动要求.

本样机拥有四条主动自由度的腿，如图12所示每条腿具备两个自由度，小腿采用了刚性结构，触地方式更容易分析，便于绘制足端的运动曲线.

图12 机器人的样机

3.2 实验结果分析

物理样机的实验可分为在线调试和脱机运行两部分，实验的大部分测试是与上位机通信的状态下进行的，可以通过多个时刻的轨迹关键点，拟合步态的曲线，运行图如图13所示.

(a)0.2 s

(b)1.3 s

(c)1.8 s图13 小跑步态实验

在样机的小跑步态实验中，观察各足部的运动情况，并记录相关参数.图13分别为0.2秒、1.3秒和1.8秒时的运行状态.可以看到，内膝肘式的四足步行机可以完成仿真的动作，测得实验结果表明行进中的速度约为35 mm/s，竖直方向的起伏较小，横向的稳定性较好，不会产生大的偏移量.样机整体长约18 cm、宽约15 cm、高约22 cm,其中大腿长8 cm、小腿长5 cm.核心板配备了通信接口，可以使用手机进行控制，在几种速度、步态间进行切换.

4 结论

本文主要对内膝肘式四足机器人进行研究，然后在ADAMS仿真环境下搭建机器人的简易样机，实现仿真实验.并就其中部分数据在物理样机上进行验证.