声速修正技术在高精度水下定位系统中的应用

李海鹏, 韩云峰，郑翠娥

声速修正技术在高精度水下定位系统中的应用

李海鹏1,2,3, 韩云峰1,2,3，郑翠娥1,2,3

（1. 哈尔滨工程大学 水声技术重点实验室，哈尔滨 150001；2. 海洋信息获取与安全工信部重点实验室（哈尔滨工程大学），哈尔滨 150001；3. 哈尔滨工程大学 水声工程学院，哈尔滨 150001）

为进一步研究声速修正技术在水声定位系统中的应用，提出1种利用声速修正技术降低测速误差改正的声线跟踪算法：分析超短基线定位的误差来源；然后以基阵中心为参考，离线计算声波从基阵中心到达作业区域所有位置的有效声速，得到1个有效声速表，保证了计算的准确性，提高了工作效率；最后进行模型误差分析。结果表明：在声线入射的几何夹角较大的情况下，有效声速法能够在保持计算速度的同时，具有较高的精度；但是随着几何夹角的减小，有效声速法的角度估计误差逐渐增大，不再适用高精度的水声定位。

超短基线；声速修正；有效声速；声线追踪

0 引言

随着各国对海洋重视程度的不断提高，水声定位系统成为人类利用众多水下航行器进入海洋、探测海洋、开发海洋的重要手段[1]，在海洋资源勘察、环境监测、海洋工程等领域扮演着越来越重要的作用。

水声定位系统按基线长度分类，可分为：长基线定位系统、短基线定位系统和超短基线定位系统[2]。超短基线定位系统通过船载声学基阵获得目标位置，然后结合全球定位系统（global positioning system, GPS）接收机、姿态传感器等外部设备进行坐标转换，以获得水下目标的大地坐标。超短基线定位系统具有组成简单、操作方便、便于大范围机动作业等优点[3]，可为水下勘探、水下目标定位跟踪、水下遥控作业等各种高精度作业提供技术支持，在海洋资源调查和科学研究领域，发挥着越来越重要的作用。

声速测量误差是影响超短基线定位精度的主要原因。由于海水介质的非均匀特性，海水中的声速随温度、盐度和深度的变化而变化，使得声波在海洋信道中传播路径是弯曲的。这意味着声波的实际传播距离要大于目标与接收基阵的几何直线距离。通过固定的声速进行定位解算必然会造成定位误差，因此需要考虑声速变化对定位解算的影响并进行修正。

文献[4]提出声线跟踪概念，并对具有线性声速梯度的介质中，声线为圆弧作了理论论证。声线跟踪法能够模拟声波在水中的实际传播轨迹，因此精度较高；但是由于对声速剖面进行分层处理，因此计算量很大。为了简化声线跟踪计算量大的问题，文献[5]提出了等效声速剖面法，用1个常梯度等效声速剖面来代替复杂的实际声速剖面，该方法虽然简化了声线跟踪过程，但也由于简化模型降低了计算精度。文献[6]提出有效声速法的概念，重新定义了声速修正模型中的声速，将水中任意2点间的有效声速，定位为2点之间的几何距离与声传播时间的比值。文献[7]提出了1种用于超短基线定位的基于有效声速表的声速修正算法，并通过外场实验进行了验证，该方法首先通过声线跟踪法离线计算作业区域所有位置的有效声速，将计算结果构成1个有效声速表，实际作业时只需要根据深度调用即可，该方法同时保证了计算精度和速度。遗憾的是，文献[7]没有详细给出算法的可行性以及适用条件。

本文通过仿真系统分析声速修正在水声定位系统中的必要性，以及声线跟踪法和有效声速法的基本原理、误差来源和适用条件，为实际工程提供参考。

1 超短基线定位原理及误差分析

1.1 定位原理

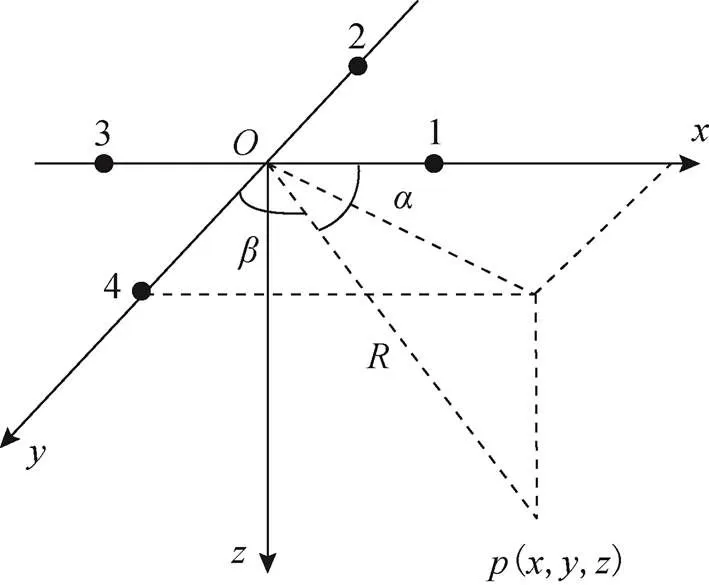
图1 超短基线定位原理

式中：为声波在水中的传播速度；为基线长度。则目标定位结果为：

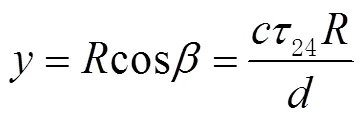
1.2 误差分析

对式（3）和式（4）进行微分并整理可得：

对式（1）和式（2）进行微分并带入式（5）和式（6）可得：

根据式（7）和式（8）可知，超短基线的定位误差的来源主要包括测距误差、测向误差和测速误差。测距误差会随着距离的增大而逐渐减小，随着夹角的增大而减小。测向误差和测速误差随着阵元间距的增大而减小。

对于超短基线而言，阵元间距受到安装条件的限制，不能无限增大。本文主要通过声速修正技术降低测速误差，通过有效声速法对传统的声线跟踪算法进行改进，提高定位精度的同时，也提高算法的运行效率。

2 声速修正算法

2.1 分层介质中的射线声学

声速在海水中呈现垂直分布特性，使得海水中的声传播轨迹发生弯曲，为了精确逼近实际的声传播轨迹，将声速剖面分层，将复杂的声速垂直分布近似为多个恒定声速梯度，因此每1层的声传播轨迹为1段圆弧，用多段圆弧来逼近真实的声传播轨迹。

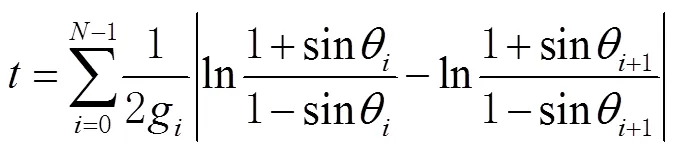
2.2 声线跟踪法

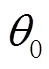
声线跟踪法的基本原理为：通过迭代算法在角度空间内进行搜索，找到声线的初始掠射角，然后根据射线声学公式，计算声传播时间和传播距离。具体流程如图2所示。

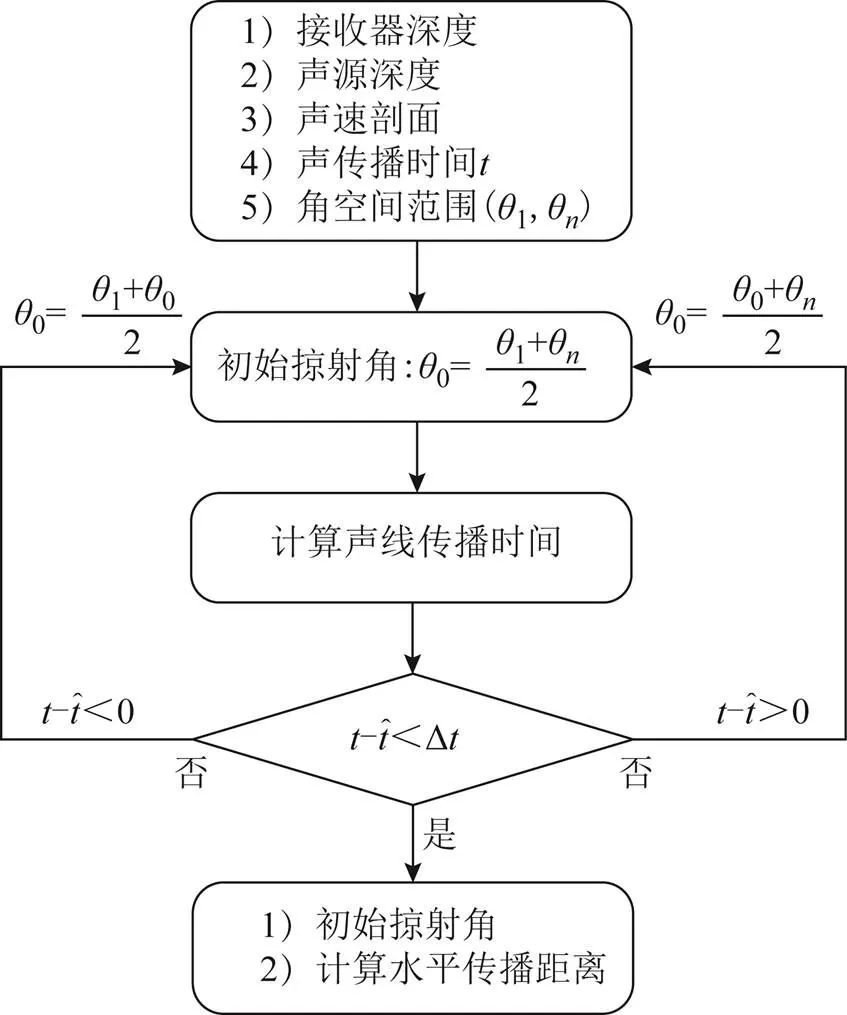
图2 声线跟踪算法流程

从图2可以看出，声线跟踪法能够模拟声波在水中的实际传播轨迹，因此精度较高；但是由于需要通过迭代进行求解，而且每次迭代都要对声速剖面进行分层计算，因此计算量很大。

2.3 有效声速法

针对声线跟踪算法精度高、计算量大的特点，文森（Vincen）提出了有效声速法的概念。有效声速的定义为有效声速等于2点之间的几何距离与实际声传播时间的比值，如图3所示。将有效声速法应用于水声定位系统，在保证精度的同时，大幅度提高了运算效率。

图3 有效声速示意

结合射线声学的计算公式，有效声速的数学表达式为

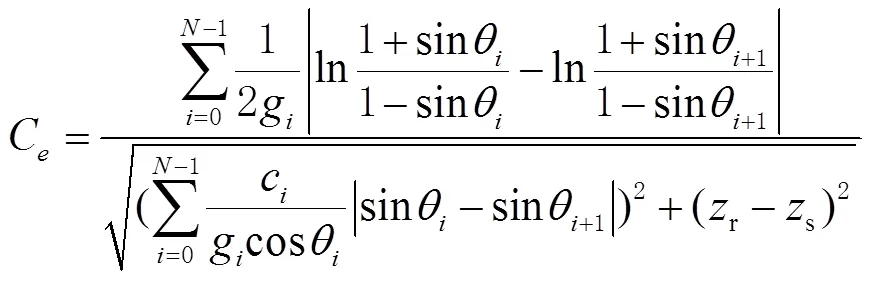
3 声速修正模型误差分析

3.1 声速修正的必要性

声线弯曲对超短基线定位精度的影响主要体现在：声线弯曲会造成声学夹角和几何夹角产生较大偏差，如果以几何夹角作为目标的方位角，必然会产生较大的定位误差，如图4所示，而且目标距离越远，定位误差越大。因此需要1种方法来消除声线弯曲对定位的影响。

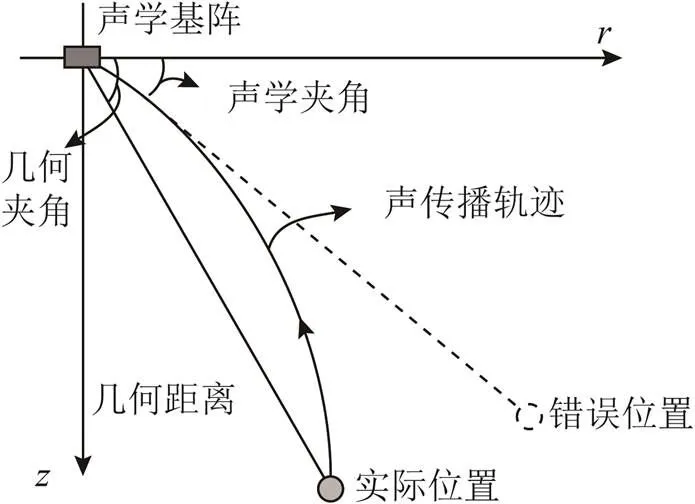
图4 声线弯曲对位置估计的影响

下面通过仿真分析声线弯曲对角度测量的影响。以图5所示的正梯度声速分布为例，假设声源深度为500 m，接收器位置为（0 m, 0 m），选取2组声速梯度为0.1和0.01的声速剖面，在该声速分布条件下，调整几何夹角大小，然后通过声线跟踪算法计算初始掠射角，并将计算结果与几何夹角进行对比，计算角度估计误差。

图5 声速剖面

图6展示了不同声速梯度下，声线弯曲对角度测量影响。

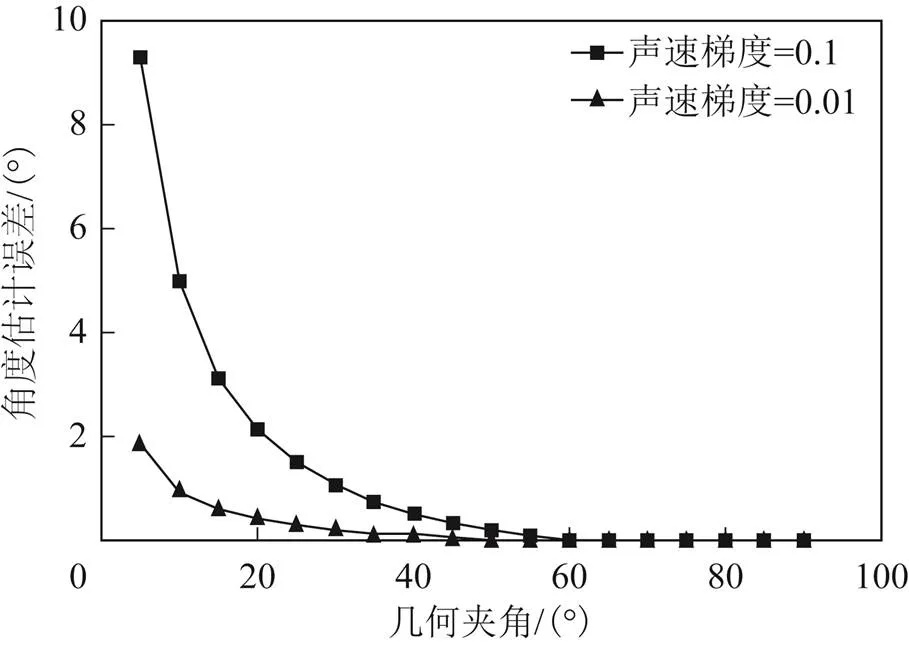
图6 角度估计误差

由图5和图6可知：在确知声速分布下，若目标与接收基阵的深度差不变，则几何夹角越小，声线弯曲对角度估计的影响程度越大；声速梯度越大，声线弯曲对角度估计的影响程度越大。

3.2 声线跟踪算法的模型误差分析

声线跟踪算法的基本原理为：采用分层介质模型模拟水下声速分布，把复杂的声速垂直分布近似由多层恒梯度声速构成，即用每个分层为等梯度的声速分布，替代连续变化的声速分布，每层用1段圆弧来逼近实际声线轨迹。

声线跟踪算法的误差主要是由分层介质模型本身带来的，而误差的大小取决于分层的数量，下面通过理论仿真来说明分层介质模型的误差特点。如图7所示，虚线为南海某海域真实声速剖面，将该声速剖面以一定的间隔进行抽样，获得图中实线。通过该模型来模拟分层介质模型带来的误差的特点。

通过图7可以直观看到分层介质假设带来的影响，即将复杂的声速分布近似为恒梯度声速分布。

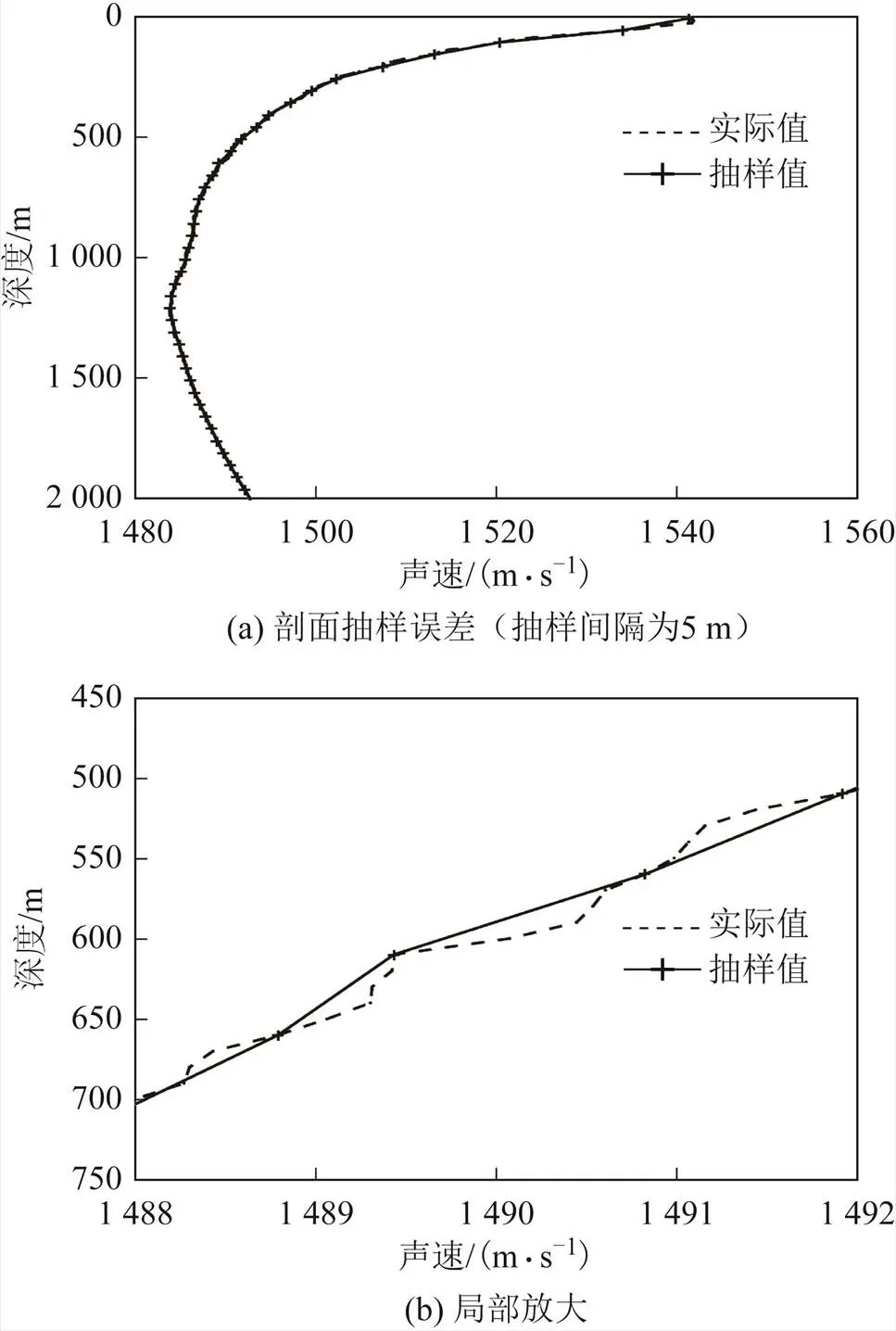
图7 分层介质模型误差特点

以图7中虚线所示的声速剖面为真实声速分布、不同抽样间隔获得的声速剖面为计算值，假设声源位于坐标原点，接收器深度为1 000 m，改变声源与接收器的水平距离由0增加至5000 m，通过声线跟踪算法，计算声学夹角与真实声学夹角的误差（如图8所示）。

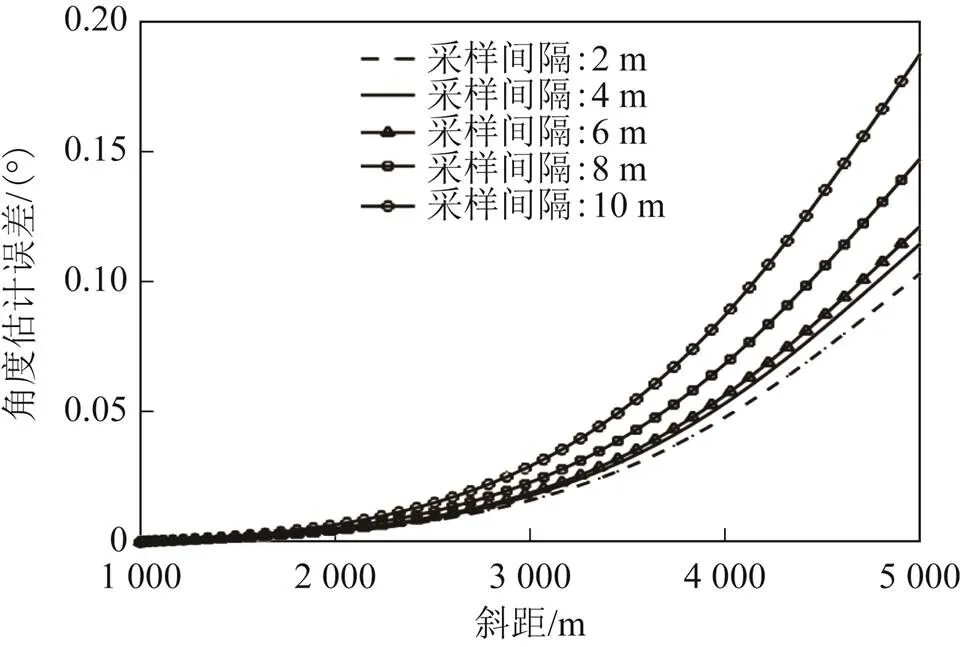
图8 声学夹角估计误差-斜距

由图8可以看出，在深度不变的情况下，随着几何夹角的减小，声源与接收器的几何距离逐渐增大，使得分层介质假设的误差随着距离的增加而逐渐累积。在相同位置，声学夹角估计误差随着抽样步长的增加而逐渐增大。

3.3 有效声速法的模型误差分析

有效声速的意义在于：将几何直线距离与弯曲的声线联系在一起，从而降低声线弯曲的影响。

以1维2元接收信号模型为例，如图9所示，1号基元坐标为（-0.05 m, 0, 0），2号基元坐标为（0.05 m, 0, 0），阵元间距为=0.1 m，目标声源深度为1000 m，声速剖面如图7中虚线所示。

图9 二元接收信号模型

上述假设会产生一定的误差，特别是在声源与接收器的距离较小时。若不采用远场假设，则真实的几何夹角应为

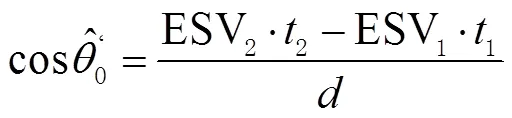
2种方法的角度估计误差分别为：

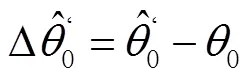
声源深度为1 000 m且保持不变，声源与接收器的水平距离由0变化至5000 m，可得到几何夹角估计误差随斜距的变化曲线（如图10所示）。图10中浅色实线表示在远场假设下，用基阵中心的有效声速代替各基元的有效声速产生的误差；深色实线表示在非远场假设下，各个基元的有效声速的计算结果。由此可见，远场假设会产生一定的误差。

下面将声速剖面进行采样从而模拟分层介质模型，仿真过程与上述内容一致。几何夹角估计误差曲线如图11所示。

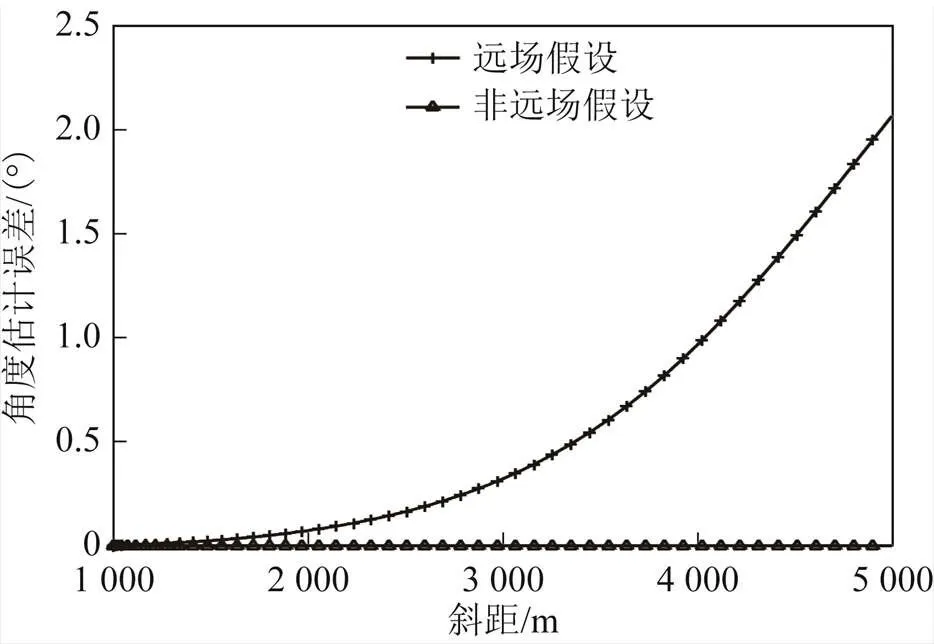
图10 远场假设下的几何夹角估计误差

图11 分层介质模型与远场假设同时存在时的角度估计误差

图11中浅色实线表示在远场假设下，用基阵中心的有效声速代替各基元的有效声速产生的误差；深色实线表示在非远场假设下各个基元的有效声速进行计算的结果。根据图10和图11可以发现，几何夹角估计误差的主要来源为有效声速的近似，由于分层介质模型造成的误差远小于由于有效声速近似造成的误差，而且由于实验条件的限制，分层介质模型造成的误差几乎无法避免。

4 结束语

本文针对现有声速修正算法中使用最普遍的声线跟踪法和有效声速法，通过计算机仿真，分析了2种方法基本原理及其造成的模型误差。根据仿真结果可以得出如下结论：

1）在深度不变的情况下，由于声速误差引起的定位误差会随着几何夹角的减小而增大，这是造成超短基线定位系统在大开角条件下定位精度较差的原因之一。

2）声线跟踪算法的模型误差的产生原因为分层介质假设，在确知声速分布情况下，声学夹角估计误差随着介质分层数的减小而逐渐增大。由于实验环境和条件的限制，分层介质模型造成的误差几乎无法避免。

3）有效声速法为了兼顾精度和效率，通常用基阵中心的有效声速代替所有接收基元的有效声速相，从而产生了误差，误差的量级也远大于声线跟踪法的模型误差。为了避免该误差，可以用每个接收基元对应的声速进行计算，但会增加相应的计算量。

根据上述结论，在实际工程中，要根据指标要求、设备状态、工作环境等因素，选择更适合的声速修正方法。

[1] 孙大军, 郑翠娥, 钱洪宝, 等. 水声定位系统在海洋工程中的应用[J]. 声学技术, 2012, 31(2): 125-132.

[2] 田坦. 水下定位与导航技术[M]. 北京: 国防工业出版社, 2007: 1-5.

[3] 冯守珍, 吴永亭, 唐秋华. 超短基线声学定位原理及其应用[J]. 海岸工程, 2002, 21(4): 13-18.

[4] KINSLER L E, FREY A R, COPPENS A B, et al.Fundamentals of acoustics[M]. 4th ed.Hoboken,NJ:John Wiley & Sons,Inc.,1999: 21-40.

[5] Geng X, Zielinski A. Precise multibeam acoustic bathymetry[J]. Marine Geodesy, 1999, 22(3): 157–67.

[6] Vincent H T, Hu S L J. Method and system for determining underwater effective sound velocity: US06388948[EB/OL]. [2019-09-20]. http: //www.freepatentsonline.com/6388948. pdf.

[7] Sun D , Li H , Zheng C, et al. Sound velocity correction based on effective sound velocity for underwater acoustic positioning systems[J]. Applied Acoustics, 2019, 151: 55-62.

[8] Urick R J. Principles of underwater sound[M]. 3rd ed. Wisconsin:McGraw-Hill Book Company, 1983.

[9] 姜婷, 张吟. 声线弯曲对水下目标定位的影响及修正方法[J]. 水雷战与舰船防护, 2015,23(1): 36-40.

[10] Ameer P M, Jacob L. Localization using ray tracing for underwater acoustic sensor networks[J]. IEEE Communications Letters, 2010, 14(10): 930-932.

Application of sound speed correction technology in highly precise underwater positioning system

LI Haipeng1,2,3, HAN Yunfeng1,2,3, ZHENG Cuie1,2,3

（1. Acoustic Science and Technology Laboratory, Harbin Engineering University, Harbin 150001, China;2. Key Laboratory of Marine Information Acquisition and Security (Harbin Engineering University), Ministry of Industry and Information Technology; Harbin 150001, China;3. College of Underwater Acoustic Engineering, Harbin Engineering University, Harbin 150001, China）

In order to further study on the application of sound speed correction technology in acoustic positioning system, the paper proposed an improved sound ray tracing method: the error sources of ultra-short base line (USBL) positioning was analyzed, and the center of the base line was taken as a reference to off-line calculate the effective sound velocity of sound waves from the center of the base array to all locations in the operation area; then an effective sound velocity table was obtained to guarantee the accuracy of calculation and improve the efficiency of work; finally the errors of the model were analyzed. Results showed that: when the geometric angle of the line incidence is large, the effective sound velocity method could have high precision with maintaining the calculation speed; but as the geometric angle decreases, the error of the angle estimation of the effective sound velocity method would gradually increase, not suitable for high-precise underwater acoustic positioning.

ultra-short base line; sound speed correction; effective sound velocity; sound ray tracing

P228

A

2095-4999(2020)03-0047-06

李海鹏,韩云峰,郑翠娥.声速修正技术在高精度水下定位系统中的应用[J].导航定位学报,2020,8(3): 47-52.（LI Haipeng, HAN Yunfeng, ZHENG Cuie.Application of sound speed correction technology in highly precise underwater positioning system[J]. Journal of Navigation and Positioning, 2020, 8(3): 47-52.）

10.16547/j.cnki.10-1096.20200307.

2019-11-22

国家重点研发计划项目（2016YFB0501700）；黑龙江省基金支持项目（YQ2019D003）。

李海鹏（1991—），男，河北承德人，博士研究生，研究方向为高精度水声定位与导航。

郑翠娥（1982—），女，湖北武汉人，博士，教授，研究方向为高精度水下定位与导航、水下传感器网络等。