从“将军饮马”问题谈起*

广东省惠州市河南岸中学(516007) 赖志萍

广东省惠州学院数学与大数据学院(516007) 王海青

1 问题的提出

“最短路径”问题属于最优化问题, 对于此类问题的探讨具有非常大的现实意义和应用价值.人教版八年级上册教材[1]在第十三章“轴对称”专门设立了有关最短路径问题的课题学习(P85-87).其目的就是结合“两点间线段最短”“直线外一点与直线上各点连线中,垂线段最短”等结论,运用轴对称的性质综合解决相应的生活实际问题,以求得最优解使解决方案最优化.

为了便于后面的论述,现将“轴对称”一章有关最短路径课题学习的问题摘抄如下.

问题1 如图1,牧马人从A地出发,赶着马群到一条笔直的河边l饮水,然后再到B地,问怎样选择饮水的地点,才能使马群所走的路径最短?

问题2 如图2,A和B两地在一条河的两岸, 现要在河上造一座桥MN, 桥造在何处才能使从A到B的路径AMNB最短?(假设河两岸平行,桥MN与河岸垂直)

图1

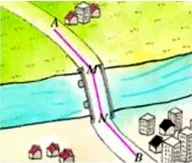
图2

问题1 也就是常说的“将军饮马”问题, 问题2 也即为“造桥选址”问题,它们都具有重要的生活实际背景和价值.

2 问题1 的解决与变式引申

分析对于问题1,教师首先需引导学生将生活实际场景转化为数学图形,从生活世界过渡到数学世界,培养学生数学建模的能力和用数学的思维解决实际问题的意识. 提取关键信息容易将图1 转化为图3.两点间线段最短, 若点A,B在直线l的两侧,则直接连接点A,点B与直线l的交点即为所求.点A,B在直线l的同侧, 可考虑移动点A到直线l另一侧的点A′,但需保证点A,A′到直线l上任一点的距离相等, 即点A′应为点A关于直线l的对称点, 如图4.连接A′B与直线l的交点P即为所求.容易证明,在直线l上任取一点P1, 根据三角形的三边关系与轴对称性质有,AP1+BP1＞AP+BP.

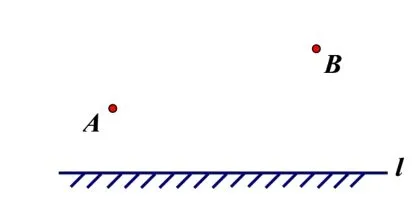
图3

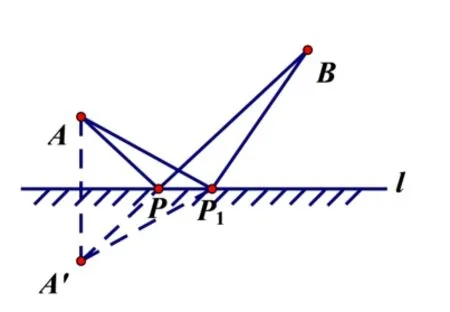
图4

到此问题1 已经解决,但教学的最终目的是使学生把握问题的本质实现方法的迁移.“将军饮马”问题的数学实质就是：已知直线l及其同侧的两个定点A,B,要在直线l上寻找一点P,使得AP+BP的值最小.解决方法是：作其中一点比如点A关于直线l的对称点A′,连接A′B与直线l的交点P即为所求.据此,可以改变“将军饮马”问题的图形结构,进行变式教学,使学生掌握并固化相应的思想方法.

变式1 如图5,正方形ABCD的边长为4,点E在边AB上,且BE= 1,P是AC上一动点,则BP+EP的最小值是多少?

图5

图6

变式2 如图6,AB是⊙O的直径,OC是与AB垂直的半径,点D是弧AC的三等分点,P是半径OC上一动点.已知⊙O的半径为1,求AP+DP的最小值.

变式3 如图7, 在直角坐标系xOy中x轴上的动点P(x,0)到定点A(4,2),B(8,6)的距离分别为PA,PB,那么当PA+PB取最小值时,点P的横坐标x等于多少?

以上变式表面上看背景与图形都大不相同,但万变不离其中,本质都与“将军饮马”问题一致.进一步地,可以对条件进行变式引申,改变动点的个数,拓宽学生的思路与视野.

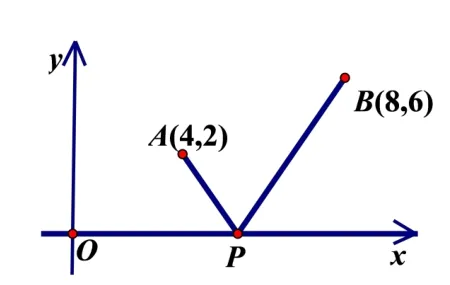
图7

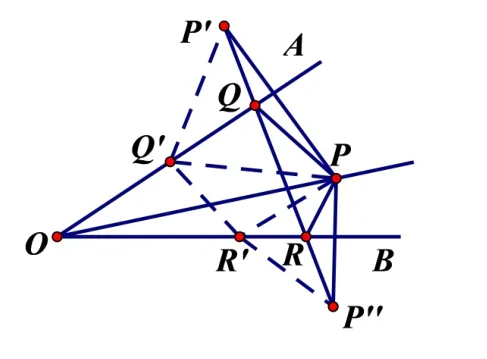
图8

变式4 如图8,∠AOB= 45°,角内有点P,PO= 10,在两边上有点Q,R(均不同于O),则ΔPQR的周长的最小值为____.

分析点Q,R未定,要使ΔPQR的周长最小可设法在保持QP,RP长不变的情况下, 将点P分别移至OA,OB的另一侧来考虑问题,使得ΔPQR的三条边刚好落在QR所在的直线上.

作点P关于OA的对称点P′,关于OB的对称点P′′.连结P′,P′′, 分别交OA,OB于点Q,R. 由轴对称的性质得：QP=QP′,RP=RP′′.ΔPQR的周长即为线段P′P′′的长. 由两点间线段最短知道, 点Q,R即为所求的点, 此时ΔPQR周长最小. 在OA,OB上分别任取一点Q′R′,ΔPQ′R′的周长=R′P′′+R′Q′+Q′P′ ＞P′P′′.

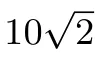
3 问题2 的解决与变式引申

问题2 本身可以看作是问题1 的另一种复杂条件的变式,转化为纯数学问题是：如图9,已知两个定点A,B在两条平行直线l1,l2的两侧,要在平行直线上找一条垂线段MN,使得AM+MN+NB的值最小.

分析平行线间的垂线段为定值, 问题转化为求AM+NB的最小值. 根据两点间线段最短, 目标转化为将AM平移至A′N,使得点M与点N重合且保证A′N与NB在同一直线上.如图10,由平行四边形的性质可知,只需求作点A′,使得AA′垂直于两平行直线且AA′=MN,连接A′B,与直线l2交于点N. 过点N作l2的垂线交直线l1于点M,MN即为所求.如图11,任作两条平行直线的垂线段M′N′,连接AM′,BN′,由三角形三边关系和轴对称的性质易得,AM′+BN′ ＞AM+NB.

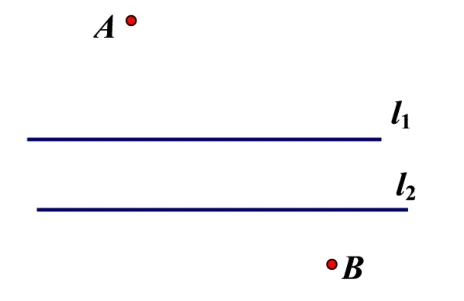
图9

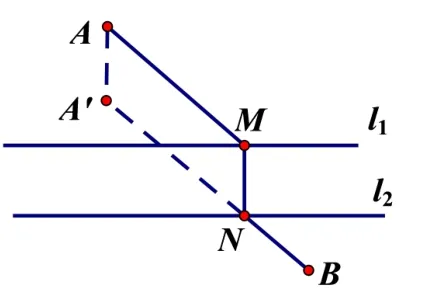
图10

图11

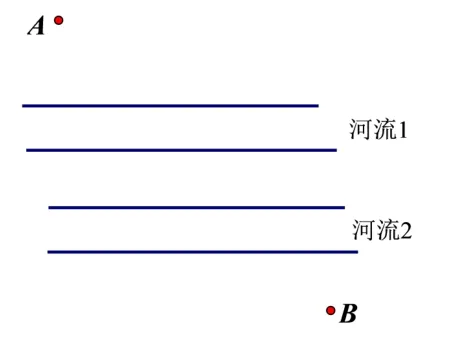
图12

进一步地,可以对问题2 的条件进行变式,考虑更复杂的现实情境.

变式5 如图12,如果A、B两地之间有两条平行的河,要建的桥都与河岸垂直,该如何找到这个最短的距离呢?

分析类比问题2 的处理思路可以找到解决方案.如图13,作AA′垂直于河流1 且使得AA′的长度等于河流1 的宽度.作BB′垂直于河流2 且使得BB′的长度等于河流2的宽度.连接A′B′,交两河流于点N,P.过点N作河流1 的垂线交另一边于点M,过点P作河流2 的垂线交另一边于点Q,MN,PQ即为所求.

图13

图14

另一种解法是, 如图14, 作AA′垂直于河流1 且使得AA′的长度等于河流1 的宽度.过点A′作A′A′′垂直于河流2 且使得A′A′′的长度等于河流2 的宽度.连接A′′B,交河流2 于点Q.过点Q作河流2 的垂线交另一边于点P. 连接A′P交河流1 与点N,过点N作河流1 的垂线交另一边于点M.MN,PQ即为所求.

沿着这个方向,可以考虑有三条平行河流、四条平行河流等情况,这里不再一一列举.继续改变条件,如果两条河不平行,又该如何建桥?

变式6 如图15,如果A、B两地之间有两条不平行的河流,要建的桥都与河岸垂直,又该如何找到这个最短的距离呢?

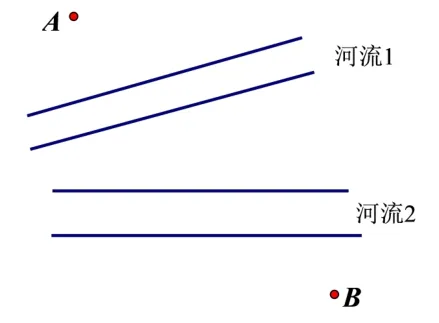
图15

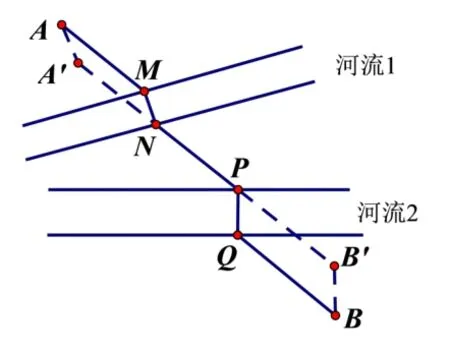
图16

分析看似条件不同,实际上问题的解决方法与变式5是一致的.如图16,作AA′垂直于河流1 且使得AA′的长度等于河流1 的宽度.作BB′垂直于河流2 且使得BB′的长度等于河流2 的宽度.连接A′B′,交两河流于点N,P.过点N作河流1 的垂线交另一边于点M,过点P作河流2 的垂线交另一边于点Q,MN,PQ即为所求.

4 总结与反思

变式教学的实质也就是落实数学家波利亚的解题思想,按照“理解题意、拟订计划、实施计划、回顾反思”[2]的四个解题步骤进行教学.通过“回顾反思”检查解题过程、优化解题方法并进行递进式的变式推广,使学生由一题通一类进而获得对知识的整体认知结构.因此,在解题中实施变式教学有助于学生掌握相应的知识与思想方法,揭示数学的本质,增强思维的深度与广度.