基于KNN的机床刀尖点频响函数预测*

张云飞，郝小忠，陈耿祥，刘 旭

（1. 南京航空航天大学机电学院，南京 210016； 2. 南京工业大学机械与动力工程学院，南京 210009）

高速切削加工（HSM）集信息、控制、材料、加工等技术于一体，具有高效、低能耗、高质量、短周期等显著优势，但是随着高速切削加工的发展，加工颤振问题也紧随而来。由于切削加工的周期性，刀具和工件之间会产生相对振动，当这种振动频率在整个切削加工系统的固有频率附近时，加工颤振就会发生。加工颤振严重限制高速切削加工技术诸多优势的发挥，严重影响工件表面质量，同时会导致机床寿命缩短、刀具磨损加剧。现有方法主要通过绘制稳定性叶瓣图（SLD）来进行颤振抑制[1–2]，而机床刀尖点频响函数则是构建稳定性叶瓣图的重要输入[3–4]。机床刀尖点频响函数对机床结构的变化十分敏感，无论是机床主轴的位置或姿态改变还是刀具/刀柄改变，机床刀尖点频响函数都可能随之变化。因此，要得到准确的稳定性叶瓣图，须得到机床全工作空间下、各种刀具/刀柄组合下的刀尖点频响函数[5]。

机床刀尖点频响函数的获取方法包括有限元法[6]，机床子结构响应耦合法（Receptance Coupling Substructure Analysis，RCSA）[7–9]以及锤击试验法。有限元法需要在仿真环境下建立机床模型，再通过模态分析即可获得机床刀尖点频响函数，但由于机床结构十分复杂，构造准确的加工系统有限元模型非常困难，实际应用时必须进行大量的简化，因此该类方法的准确性难以得到保证。RCSA方法将机床分解为若干个子结构，然后分别针对每个子结构选取合适的方式获取其频响函数，最终将这些子结构的频响函数进行柔性或者刚性耦合以预测机床刀尖点的频响函数。这种方法可以比较高效地获取机床刀尖点频响函数，但是机床子结构之间的连接状态模型和连接参数的辨识一直是该方法的难题。到目前为止，学者们提出了各种各样的连接状态模型，其中有单点弹簧阻尼模型[10]，两点弹簧阻尼模型[11]，均布弹簧阻尼模型[12–13]，以及弹性层面模型[14]等。相应的，连接参数的辨识方法也有很多种，包括非线性优化算法求解[15–16]，RCSA方法逆求解[17–18]等。总之，连接状态模型和连接参数的辨识方法还处于研究阶段，距离工程应用还有一定差距，RCSA方法的准确度也有待进一步提高。

锤击试验法是获取机床刀尖点频响函数的经典方法，基于该方法可以得到准确的测量结果。但是使用这种方法进行一次测量只能得到一个主轴位置处、一种刀柄–刀具组合状态下的刀尖点频响函数。如果刀柄、刀具或者机床主轴位置发生改变，就需要重新进行测量。因此，如果使用锤击试验法测量机床全工作空间下、各种刀具/刀柄组合下的刀尖点频响函数，必须要求机床长时间停机，这显然难以满足实际生产要求。

目前，在关于机床刀尖点频响函数的研究中，多数学者都热衷于发展RCSA方法，锤击试验法却鲜有人问津。但事实上，近年来多种回归算法大力发展，如果将其和锤击试验法相结合，便能够在确保预测精度的同时大大减少锤击试验次数，因此本文提出了一种基于KNN的机床刀尖点频响函数预测方法。

1 机床刀尖点频响函数预测模型

1.1 机床结构变化对刀尖点频响函数的影响

机床刀尖点频响函数是整个机床系统在刀尖位置的动力学特性的综合体现，因此机床刀尖点频响函数对机床整体结构的变化十分敏感。在实际加工过程中机床结构变化主要表现为两种情况，第1种是机床主轴位置和姿势（简称位姿）变化，第2种则是机床刀具或者刀柄的更换。这两种情况都会导致机床刀尖点频响函数的变化，以下分别对前述两种情况引起的机床刀尖点频响函数的变化进行试验验证。

首先考虑第1种情况，在1台试验机床上(机床坐标系如图1所示)装夹直径为10mm，悬伸长度(定义如图2所示)为56mm的刀具，然后保持机床X、Y、Z、C轴不变，将A轴从0转动到90°，期间每隔10°通过锤击试验法测量其刀尖点频响函数，并将这些频响函数进行集中对比，如图3所示。刀尖固有频率附近区域的频响函数对颤振抑制具有重要意义，因此本文主要考察该区域的频响函数，图3所展示的是1000Hz附近的频响函数曲线。

图1 试验机床坐标系Fig.1 Coordinate system of experimental machine tool

图2 刀具悬伸长度和装夹长度Fig.2 Tool overhang and clamping length

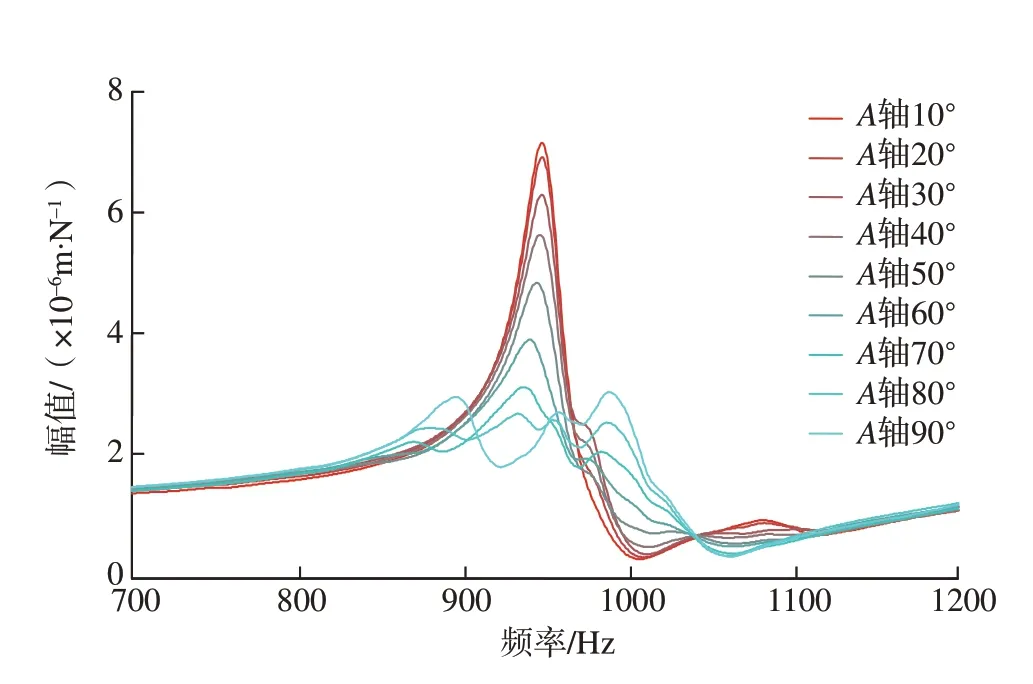
图3 机床位姿引起的刀尖点频响函数变化Fig.3 Change of tool tip FRF caused by varying machine tool postures

对于第2种情况，使用一系列带螺纹的圆柱棒来研究不同刀具引起的刀尖点频响函数的变化，如图4所示。将图4中左侧带外伸螺纹的圆柱棒作为刀具装夹部分插入刀柄，其余圆柱棒则作为刀具伸出部分。保持机床位姿不变，依次更换外伸圆柱棒，并采集其刀尖点频响函数，将其对比如图5所示。

基于以上分析和验证可以得出结论，机床刀尖点的频响函数随机床结构的变化而变化。本文拟使用回归算法对不同机床结构下的刀尖点频响函数进行拟合，得到刀尖点频响函数预测模型，从而对机床不同结构下的刀尖点频响函数进行预测。

1.2 刀尖点频响函数数据集定义与获取

由1.1节可知，刀尖点频响函数受机床主轴位姿和刀柄/刀具影响，主轴位姿信息可以用机床坐标表示，而刀具信息中对刀尖点频响函数影响最大的是刀具直径和其悬伸长度，此处选取这两个数据表示刀具信息。因此，本文数据集中的特征数据x包括刀具直径、刀具悬伸长度以及机床主轴坐标。

图4 螺纹连接分段圆柱棒Fig.4 Threaded segmented cylinders

图5 不同刀具引起的刀尖点频响函数变化Fig.5 Change of tool tip FRF caused by varying tools

而对于刀尖点频响函数信息而言，有两种方式可以选择，一种是对其进行模态参数辨识，然后将得到的参数作为标签，有一些学者已经在研究中采用这种方式来表示频响函数信息[6,19]。第2种方式则是直接选取固有频率附近频率段内的频响函数曲线离散点作为标签。第1种方式的显著优点是数据量小，更易于回归训练，但无法有效表达频响函数的模态阶数。如图3所示，在固有频率附近频率段内，主轴位姿不同，刀尖点频响函数的模态阶数也不尽相同，所以很难使用统一阶数的模态参数来表示频响函数信息。对于第2种方式，虽然作为回归数据集的数据量较大，但其可以有效表达所有频响函数的模态阶数。综上所述，本文选取第2种方式来表示标签数据y，即机床刀尖点固有频率附近频率段内的频响函数曲线离散点。而最终通过回归算法得到的刀尖点频响函数预测模型可以表示为f：x→y。

刀尖点频响函数是在机床整体结构的变动范围内持续变化的，训练数据集最好能够反映机床结构变动范围内刀尖点频响函数的整体变化趋势。另外，标签中并不需要整个频谱的刀尖点频响函数曲线，只需要得到刀尖点固有频率附近的部分曲线即可。基于以上考虑，本文在机床主轴可移动范围内均匀选取少量坐标点，并选取加工过程中使用频率较高的刀具直径和悬伸长度数据作为特征数据，选取机床刀尖点固有频率附近的部分频响函数曲线段离散点作为标签数据。

1.3 KNN的基本要素

KNN算法凭借其简单和准确的特点被广泛应用，其基本思想是计算特征空间中样本点之间的相似程度，并根据这种相似程度进行预测[19]。样本点之间的相似程度是用距离表示的，而距离度量方式则是KNN算法的3个基本要素之一。

KNN算法中的距离度量通常选择Lp距离（Lpdistance）：

其中，xi，xj∈A，A是特征空间，即n维实数向量空间xi=。

当p=2时，式（1）就 是 欧 式 距 离(Euclidean distance)的表达式，即

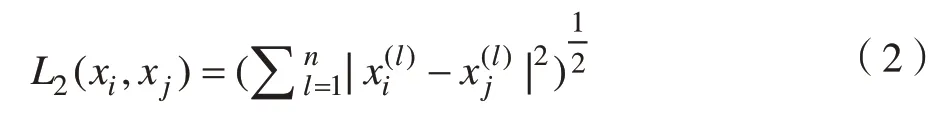
当p=1时，式（1）就是曼哈顿距离(Manhattan distance)的表达式，即

本文采用欧式距离作为KNN算法的距离度量方式。

KNN的另外两个基本要素是k值和回归预测规则。k值的选择会显著影响KNN算法的结果，如果k值过小，预测结果受临近点的影响就会加大，也就更容易发生过拟合。反之，如果k值过大，则容易发生欠拟合。实际应用时，一般会选择较小的数赋给k。KNN算法的回归预测规则一般采取平均值法或者加权平均值法。平均值法即获得k个临近点，将其目标值平均后作为预测值。加权平均值法则按照临近点与待预测点的距离给每个临近点的目标值加权，一般情况下距离和权重成反比，之后再进行平均得到预测值。本文选取平均值法作为回归预测规则。

1.4 kd树搜索临近点

由于本文训练数据集的数据量较大，必须考虑临近点搜索的效率。KNN算法中通常使用线性扫描（Linear Scan）来实现k个临近点的查找，但是训练数据量较大时，这种搜索方式的效率很低。k-dimensional树（kd树）可以有效提高临近点的搜索效率。

kd树是一种二叉树，它可以通过一系列垂直于坐标轴的超平面将k维空间划分成不同的区域。图6中以2维空间kd树的建立为例解释其具体实现方式，其中圆点对应2维空间中的样本点，直线对应区域的划分线（即前文所述超平面）。将整个k维空间作为根结点，然后选择切分点构造划分线，将整个区域进行划分，划分完成的每个子区域都对应一个子结点，按照此方式继续划分，直到所有子区域都不包含样本点为止，将终止时的结点称为叶节点。

构建kd树的伪代码如下：

算法：建立kd树

输入：数据集"Data" 和其所属空间A

输出：kd树

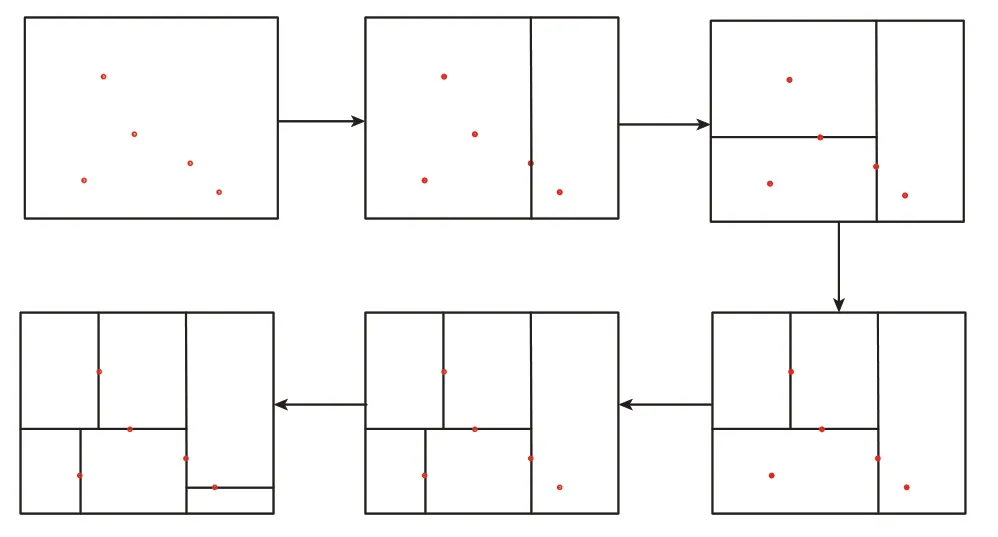
图6 2维空间kd树Fig.6 2D space kd tree

（1）If"Data" 为空，则返回的kd树为空

（2）构造子结点：

确定划分维度：统计"Data" 在每个维度上的方差，方差越大表明数据在该维度上越分散，越适合数据分割。

确定切分点：将"Data" 按照所选维度进行排序，并选择中间的数据点作为切分点。

划分子区域：通过切分点垂直于维度坐标轴作超平面，从而将整个区域（对应根结点，即空间A）划分成两个子区域，在坐标轴上小于切分点的子区域成为左子结点，否则为右子结点。

（3）重复划分区域：重复步骤（2）进一步划分区域，直到两个新产生的子区域没有数据点存在为止，最终的子区域成为叶结点。

对于一个待预测点，首先在kd树中找到其所属的叶结点，并将其作为当前最邻近点，然后以待预测点到当前最邻近点的距离为半径，以该待预测点为球心绘制超球体，则实际最邻近点肯定在该超球体内部。随后从叶结点出发，依次退回到上级结点，不断查找并更新当前最邻近点，直到确定没有更邻近的样本点为止。可以发现，kd树搜索临近点的整个过程中，只计算了待预测点和其所在的局部区域内的样本点的距离，大大减少了距离求解的计算量，适合训练集数据量大的应用场景。

搜索kd树的伪代码如下：

算法：搜索kd树

输入：kd树和目标点s

输出：kd树

（1）确定目标点所属的叶结点：从根结点开始，逐步访问下级子结点，逐个对比s和切分点的当前维度坐标，以确定前往左子结点还是右子结点，直至找到叶结点，并以此叶结点作为当前最临近点。

（2）更新当前最临近点：

建立搜索超球体：以s和当前最邻近点的距离为半径，以s为球心建立搜索超球体；

搜索更邻近点：逐步往上级结点回退，并判断当前结点对应的区域是否与搜索超球体相交，如果相交，就在相交区域寻找样本点并更新当前最近临近点，否则就维持当前最近临近点不变。

（3）重复步骤（2）直到退回到根结点，并将最新的当前最邻近点作为目标的最临近点。

1.5 KNN算法实现

在本文的应用场景下，KNN算法步骤如下：

（2）采用式（2）所示的欧式距离为距离度量方式，对于一个测试数据集xj，此时具体的距离表达式应该为：

通过kd树确定距离该测试集最近的k个训练集，将这些训练集中的目标值记为。

（3）对上述k个邻居的目标值进行平均，并将其作为最终预测结果。

2 试验验证

2.1 试验环境

本文所提方法在一台五轴机床上进行了试验验证，图7是锤击试验系统，该五轴机床包括X、Y、Z 3个平动轴，和A、C两个转动轴，其中C轴的可移动范围是0～360°，A轴的可移动范围是0～90°。初步试验表明，该机床移动轴移动对刀尖点频响函数的影响不大，所以此次验证选择在旋转轴上进行。

验证过程中需要用的3把刀具信息，如表1所示。

2.2 试验结果

控制机床的平动轴不动，选取A轴每隔20°（从0开始），C轴每隔120°（从0开始）的主轴位姿处为待测坐标点，数量为20。在机床上分别装夹1～3号刀具，如图8所示。通过锤击试验获得3把刀具在待测坐标点处的刀尖点频响函数G11,tt，其中tt代表频响函数矩阵的第1行第1列元素，即位移/力频响函数。每次锤击试验都连做5次，并将其结果的平均值作为该次试验的最终结果。将刀具直径d，刀具悬伸长度l，机床A轴坐标a，C轴坐标c，刀尖点固有频率附近的离散频率w以及G11,tt的绝对值g11作为回归训练集，其形式为{di, li, ai, ci, wi, g11i}。将训练数据集用基于kd树的KNN算法进行回归训练，经过交叉验证，此处取参数k的值为5。回归模型训练完毕后，保持机床移动轴坐标不变，另取4个机床坐标点：C0A10°、C60°A90°、C180°A50°以及C300°A70°，再结合上述3把验证刀具信息以及刀尖点固有频率附近离散频率数据，构造成形式为{di, li, ai, ci, wi}的测试集对回归模型进行测试。

另外，本文还使用RCSA方法，预测了验证刀具在机床4个测试位姿处的刀尖点频响函数。RCSA是一种可以高效获得刀尖点频响函数的方法。使用该方法求刀尖点频响函数时，一般可以将机床分解成主轴–刀柄系统和刀具伸出部分（或者主轴–部分刀柄系统，外伸刀柄和刀具伸出部分）。接着通过锤击试验法获得主轴–刀柄系统频响函数，再使用有限元法或者解析法获得刀具伸出部分的频响函数，然后再使用式（7）将各个子结构的频响函数耦合即可得到刀尖点频响函数。

表1 验证刀具Table 1 Tools for experimental verification

图8 G11,tt测量方法Fig.8 Measurement method of G11,tt

其中，G11表示机床刀尖点的频响函数；H11和H22分别表示刀具在自由状态下在两头端点处的原点频响函数；H12和H21则表示刀具在自由状态下在两头端点处的跨点频响函数；H33表示耦合之前主轴–刀柄系统在刀柄端点处的原点频响函数，K–1则表示刀柄和刀具之间的连接处特性。

依次将1～3号刀具装夹到机床上，利用锤击试验测量机床4个测试位姿处刀尖原点频响函数G11,tt和跨点频响函数G12,tt。在机床坐标C0A10°处，使用Park在文献[18]中提出的IRCSA（Inverse Receptance Coupling Substructure Analysis）方法辨识连接处特性K–1，并利用所得连接处特性预测其他3个测试位姿处的刀尖点频响函数。

随后，将本文方法预测的刀尖点频响函数曲线，基于RCSA方法预测曲线以及利用锤击试验得到的曲线进行对比，结果如图9～11所示。图9所示是1号刀具的测试结果，可以发现，在图9（a）中，本文所提方法和基于C0A10°处连接处特性使用RCSA方法（简称IRCSA–Park方法）的预测效果都比较好，而在图9（b）～（d）中，本文所提方法则表现出了明显的优势。

另外，表2中对1号刀具的试验结果进行了定量分析，其中主要对比了本文方法、IRCSA–Park方法以及试验法所得刀尖频响函数的固有频率和单/多模态（即主要模态峰的个数）。对比数据表明，当试验法得到的频响函数曲线是单模态时，本文方法和IRCSA–Park方法的预测曲线也是单模态的，其中，和试验频响曲线的固有频率相比，本文方法最大误差是4Hz，IRCSA–Park方法最大误差则是10Hz。当试验频响函数曲线为多模态时，本文方法预测曲线也是多模态的，而IRCSA–Park方法预测曲线则是单模态的，同时本文方法预测曲线和试验曲线主要模态峰的固有频率都相差很小。

图10是2号刀具的测试结果，可以发现，在图10 （a）中，本文所提方法预测效果比基于C0A10°连接处特性使用RCSA方法的预测效果稍差，但也保持了较好的准确度。观察图10（b）～（d），在频响函数的第1个峰处，本文所提方法和基于C0A10°连接处特性使用RCSA方法的预测效果都比较好，而在第2个峰处，本文所提方法预测效果更好。

图9 1号刀具在机床4个测试位姿处的刀尖点频响函数对比Fig.9 Comparison of tool tip FRF of No. 1 tool at 4 test positions

表2 1号刀具刀尖点频响函数定量分析Table 2 Quantitative analysis of frequency response function of tool tip of No.1 tool

表3和表4中对2号刀具的试验结果进行了定量分析。对比数据表明，对于频响曲线的第1个峰，试验曲线、本文方法预测曲线以及IRCSA–Park方法预测曲线都为单模态，其中，与试验频响曲线的固有频率相比，本文方法最大误差是17Hz，IRCSA–Park方法最大误差则是15Hz。

对于频响曲线的第2个峰，试验曲线和本文方法预测曲线全是单模态的，而IRCSA–Park方法预测曲线则在很多情况下都是多模态的，同时本文方法预测曲线和试验曲线的固有频率最大相差11Hz。

图11所示是3号刀具的测试结果，可以发现，在图11（a）中，本文所提方法预测效果比基于C0A10°连接处特性使用RCSA方法的预测效果稍差，但也保持了较好的准确度。观察图11（b）～（d），在频响函数的第1个峰处，相比于基于C0A10°处连接处特性的RCSA方法，本文所提方法效果更好，而在第2个峰处，两种方法预测效果都比较好。

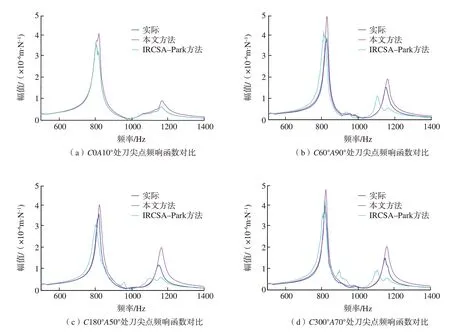
图10 2号刀具在机床4个测试位姿处的刀尖点频响函数对比Fig.10 Comparison of tool tip FRF of No. 2 tool at 4 test positions

表3 2号刀具刀尖点频响函数第1个峰定量分析Table 3 First peak of tool tip FRF numerical analysis of No. 2 tool

图11 3号刀具在机床4个测试位姿处的刀尖点频响函数对比Fig.11 Comparison of tool tip FRF of No. 3 tool at 4 test positions

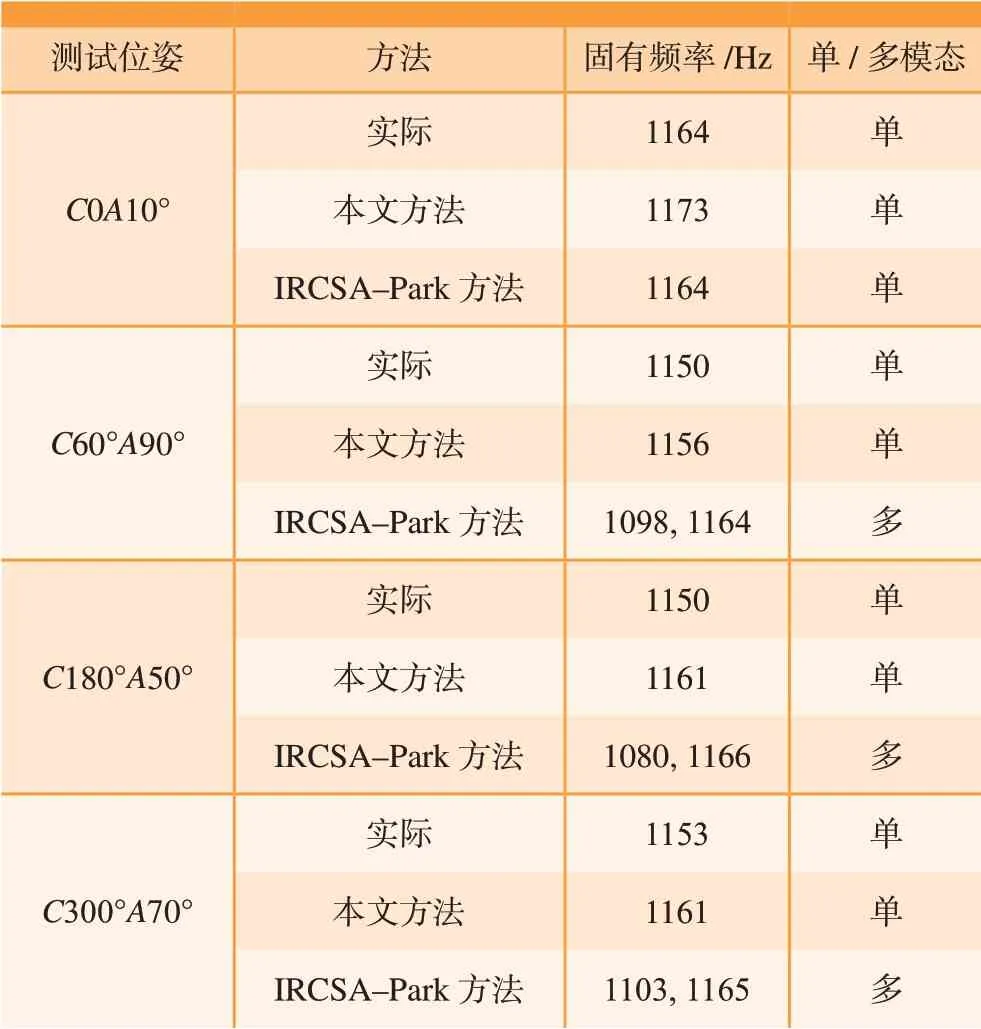
表4 2号刀具刀尖点频响函数第2个峰定量分析Table 4 Second peak of tool tip FRF numerical analysis of No. 2 tool

表5和表6中对3号刀具的试验结果进行了定量分析。对比数据表明，对于频响曲线的第1个峰，当试验曲线是单模态时，本文方法和IRCSA–Park方法的预测曲线也是单模态的，其中，和试验曲线的固有频率相比，本文方法最大误差是7Hz，IRCSA–Park方法最大误差则是27Hz。当试验曲线为多模态时，本文方法预测曲线也是多模态的，而IRCSA–Park方法预测曲线则是单模态的，同时本文方法预测曲线和试验曲线的固有频率最大相差8Hz。

对于频响曲线的第2个峰，试验曲线、本文方法预测曲线以及IRCSA–Park方法预测曲线都为单模态，其中，和试验频响曲线的固有频率相比，本文方法最大误差是20Hz，IRCSA–Park方法最大误差则是13Hz。

表5 3号刀具刀尖点频响函数第1个峰定量分析Table 5 First peak of tool tip FRF numerical analysis of No. 3 tool

表6 3号刀具刀尖点频响函数第2个峰定量分析Table 6 Second peak of tool tip FRF numerical analysis of No. 3 tool

3 结论

机床刀尖点频响函数对机床结构的变化十分敏感，无论是机床主轴的位置改变还是刀具/刀柄改变，机床刀尖点频响函数都会随之变化，导致机床刀尖点频响函数的获取过程十分繁复。针对这个问题，本文提出了一种基于KNN的机床刀尖点频响函数预测方法，并在一台五轴机床上对所提方法进行了验证，试验结果表明：

（1）在锤击试验法的基础上，本文所提方法大幅提高了获取刀尖点频响函数的效率。

（2）相比于RCSA方法，本文所提方法的预测结果具有更好的准确性。