平均差分进化算法在等效系统拟配中的应用

田宏峰, 薛 源,2, 徐浩军, 杨梓鑫, 吴嘉杰

(1.空军工程大学航空工程学院， 西安， 710038； 2.西北工业大学航空学院， 西安， 710129； 3.95960部队， 西安， 710089)

现代战斗机由于在气动布局、结构、动力系统等方面应用了较多的先进技术同时增加了控制增稳系统[1]，引入了各类前馈和反馈补偿器，导致飞机组合系统的特征方程的阶次越来越高，描述飞机动力学模型不再是具有典型模态的低阶系统而是高达50～70阶的高阶系统。评价此类高阶系统的飞行品质通常采用的是等效系统法[2]，飞行品质规范[3-4]对等效系统准则作了相关的规定。等效系统法是将飞机的操纵系统和飞机本体组成的高阶系统等效拟配成体现典型模态特性的低阶系统，从而依据飞行品质规范进行等级评定。

Morelli, Eugene A[5]采用不同的输入将方程误差法和输出误差法相结合对等效系统进行辨识，提出了一种新的等效系统拟配方法,但是未考虑数据中存在的噪声影响。Timothy J.C[6]利用非线性方程误差公式来辨识等效系统的参数，取得了一定的研究成果，但是计算过程较为复杂，实现难度较大。江飞鸿等[7]提出了一种新的等效系统初值计算方法，虽然精度比传统的最小二乘法和极大似然法有所提高，但是仍然存在容易陷入局部最优解。章萌等[8]虽然利用混沌差分进化算法对等效系统拟配进行了研究，得到的拟配精度相较于传统的辨识算法有了提高，但是未考虑应用混沌差分进化算法来处理存在噪声的数据。

目前常规的等效系统拟配方法是最小二乘法[9]和极大似然法[10]，但是这两种方法仍然存在着初值要求较高，全局寻优的能力较差，对带噪声数据处理能力较差的问题。针对这些问题，本文提出了应用平均差分进化算法来进行等效系统拟配的新思路。

1 平均差分进化算法

本文在研究差分进化算法进行等效系统拟配的基础上，基于种群平均水平加上当前个体最优解与个体之间的差异值权重的思想，对差分进化算法提出了改进，得出了平均差分进化算法。

1.1 基本步骤

1.1.1 生成初始群体

在n维空间里随机产生满足约束条件的M个个体，实施措施如下：

(1)

1.1.2 变异操作

变异操作的公式为差分进化算法以及平均差分进化算法的核心公式，本文所提的平均差分进化算法主要是对差分进化算法变异操作的公式进行改进，从而提高等效系统拟配的精度。

从群体中随机选择3个个体x1，x2和x3，对于本文所提的平均差分进化算法的变异操作为：

hi(t+1)=

F(x1(t)-x3(t))+0.5(x2(t)+x3(t))

(2)

如果无局部优化问题，平均差分进化算法的变异操作可写为：

hi(t+1)=

F(xbestS(t)-x3(t))+0.5(x2(t)+x3(t))

(3)

对于差分进化算法的变异操作为：

hi(t+1)=x1(t)+F(x2(t)-x3(t))

(4)

如果无局部优化问题，差分进化算法的变异操作可写为：

hi(t+1)=xbestS(t)+F(x2(t)-x3(t))

(5)

式中：0.5(x2(t)+x3(t))代表的是此时种群的整体水平；x2(t)-x3(t)为种群的差异化程度；xbestS(t)-x3(t)表示种群初始最优个体与种群个体之间的差异程度；F为变异因子；xbestS(t)表示当前种群中最好的个体，可明显提高收敛速度。

1.1.3 交叉操作

交叉操作是为了增加群体的多样性，具体操作如下：

(6)

式中：rand(0，1)为[0,1]之间的随机小数；cr为交叉概率，cr∈[0,1]。

1.1.4 选择操作

为了确定目标个体xi(t)是否成为下一代的成员，将交叉操作得到的试验个体vi(t+1)和目标个体xi(t)通过目标函数进行比较：

(7)

反复执行1.1.2至1.1.4，直至达到最大迭代次数G,平均差分进化算法基本运算流程见图1。

图1 平均差分进化算法流程图

从图1可以看出平均差分进化的基本思想是：利用父代个体的变异操作产生变异个体，然后以一定的概率，在父代和变异个体之间进行交叉操作得到试验个体，再根据试验个体与父代个体之间的适配度进行选择操作，保留最优解，实现种群进化。

1.2 参数设置

1)变异因子。变异因子F是控制种群多样性和收敛性的重要参数，本文经过大量测试得出F=0.9～1.4时精度较高，收敛速度较快，扩大了差分进化算法的变异因子。

2)交叉因子cr。交叉因子cr可控制个体参数的各维对交叉的参与程度，以及全局与局部搜索能力的平衡，cr既不能太大，也不能太小，经过大量试验发现在[0.6,0.9]的范围内效果最好。

3)群体规模M。一般选取[20,50]。

4)最大的迭代次数G。迭代次数越大，最优解越精确，但同时计算时间会更长，需要根据具体问题设定。

2 基于平均差分进化算法的等效系统拟配

2.1 输入设计

飞行器参数辨识的可靠性和准确度很大程度上是由于输入设计的影响，本文采用的是3-2-1-1输入，该输入为驾驶员常用的输入之一，应用到等效系统辨识中具有重要代表意义，同时也适用于本文的等效系统拟配。见图2。

图2 3-2-1-1输入图

由于真实的数据中存在一定的噪声，为验证本文方法在实际工程中的高拟配精度，在3-2-1-1输入的基础上分别加入了10%、30%的白噪声[11]来验证本方法在等效系统拟配中的高精度。

图3～4分别为加入10%、30%的白噪声后的输入,可以看出随着白噪声比例增加，原本3-2-1-1输入的幅值波动越大，从图中可以看出加入白噪声后较为贴近实际的数据情况，对本文的研究有重要意义。

图3 加入10%白噪声输入

图4 加入30%白噪声输入

2.2 平均差分进化算法拟配过程

2.2.1 等效系统

本文已知带控制器的某型飞机俯仰角速度对纵向驾驶杆力的高阶数学模型[12]：

(8)

本文假设等效低阶系统的数学模型：

(9)

式中：n为所选取的频率点数；ωn为无阻尼自振频率，拟配的频率范围选取0.1～10 rad/s

在频率域内进行等效系统拟配，目标函数(在本文的平均差分进化算法中为适应值)为:

ξ[Φhos(ωi)-Φlos(ωi)]2}

(10)

式中：Ghos,Φhos分别为高阶系统频率特性的幅值和相位；Glos,Φlos分别为低阶系统频率特性的幅值和相位；ξ表示幅值偏差和相位偏差之间相对重要性的加权因子，一般取为0.017 45 dB/(°)。

2.2.2 拟配过程

本文应用平均差分进化算法进行等效系统拟配，将等效系统拟配的目标函数作为平均差分进化算法的适应值，通过比较目标函数(即适应值)的大小来进行最优个体的判断。

1)设置参数。设置参数搜索范围、种群规模和参数个数、变异因子、交叉因子以及最大迭代次数。

2)利用初始化参数计算个体适应值J(Xi)，进行对比得出个体最优Pi，将适应值最好的个体作为初始的全局最优。

3)变异操作。根据平均差分进化算法的核心公式(2)、(3)更新个体的状态。

4)交叉操作。按照式(6)对每个个体进行交叉操作，得到试验个体vi(t+1)。

5)如果试验个体的适应值J(Xi)低于当前个体最优Pi的适应值，则试验个体vi(t+1)更新为新位置，反之，Pi保持不变。

6)循环迭代。检查结束条件，若满足，则寻优结束，输出全局最优个体Pg和最优适应值；若未达到最大收敛代数，则返回步骤3)，结束条件为寻优达到的最大进化代数tmax，或适应值小于给定精度。

2.2.3 仿真分析

根据上述的平均差分进化算法的拟配过程，本文进行的等效系统拟配主要有4个未知需要辨识的参数，分别是k，a，ζ，ωn。依据对低阶等效系统的参数进行估计来设置参数的搜索区间，其中k∈[-5,5]，a∈[-1,1]，ζ∈[-3,3]，ωn∈[0,30]。

首先对3-2-1-1输入信号应用最小二乘法、极大似然法、差分进化算法以及本文提出来的平均差分进化算法来进行等效系统拟配(见图5～8)，得出4种方法的辨识参数值表1。

图5 应用最小二乘法得到的等效系统拟配图

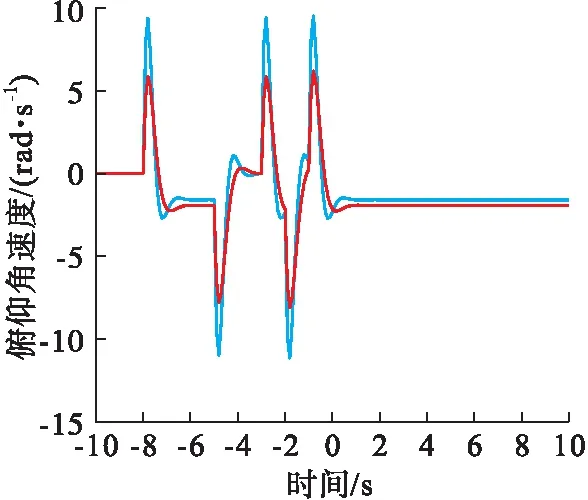
图6 应用极大似然法得到的等效系统拟配图

图7 应用差分进化算法图得到的等效系统拟配结果图

图8 应用平均差分进化算法图得到的等效系统拟配图

表1 4种方法的辨识参数值

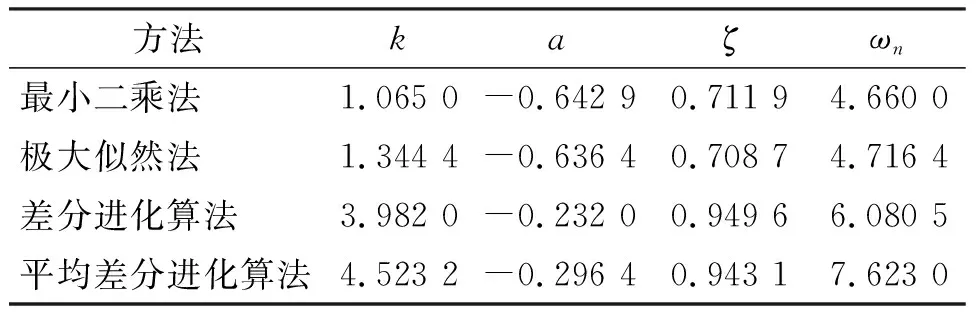
方法kaζωn最小二乘法1.065 0-0.642 90.711 94.660 0极大似然法1.344 4-0.636 40.708 74.716 4差分进化算法3.982 0-0.232 00.949 66.080 5平均差分进化算法4.523 2-0.296 40.943 17.623 0

从图5～8可以看出极大似然法和最小二乘法在对初值进行估计的基础上具有一定的辨识效果，但是精度不是很高，而且对初值的依赖性较高，容易陷入局部最优解。但是对于差分进化算法则不需要考虑初值的影响，而且差分进化算法具有良好的全局寻优能力，通过仿真可以得出差分进化算法的精度比最小二乘和极大似然法的精度要高，说明差分进化算法能够应用到等效系统拟配中并且可以取得较好的拟配效果。差分进化算法虽然有较好的效果，但是在相同输入的前提下低阶系统的输出跟高阶系统的输出相比仍然存在一定的误差，而应用本文提出的平均差分进化算法计算得到的仿真图则具有较为理想的拟配效果，低阶系统和高阶系统的输出误差较小，在保证高精度的同时也解决了初值依赖性高，易陷入局部最优解的问题。说明本算法的改进较为合理，提供了一种新的高精度等效系统拟配方法。

上述计算结果的输入为理想型的3-2-1-1，但是考虑到真实的飞行数据中存在着噪声，为了验证本文的算法在工程实际中的作用，在原有3-2-1-1输入的基础上加上10%、30%的白噪声，等效系统拟配情况见图9～11。

图9 加入不同白噪声后应用最小二乘法得到的拟配图

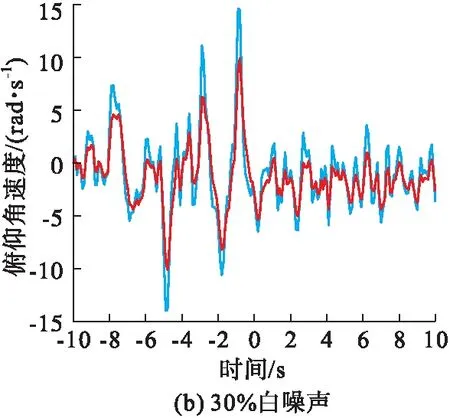
图10 加入不同白噪声后应用极大似然法得到的拟配图

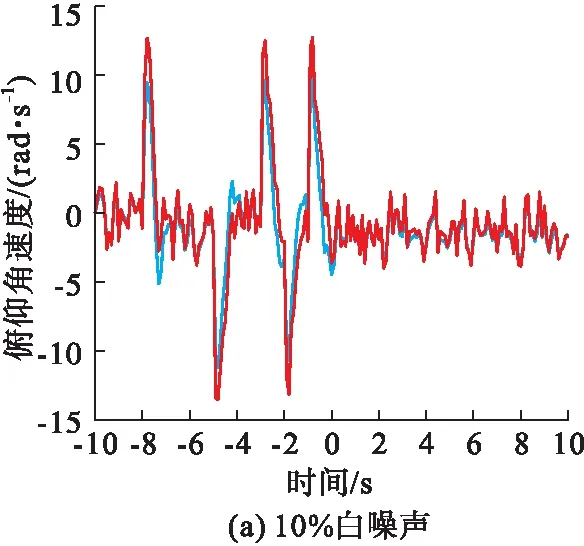
图11 加入不同白噪声后应用差分进化算法得到的拟配图

从图9～11可以看出随着白噪声比例的增加，最小二乘法、极大似然法拟配的精度逐渐降低，同时波动的幅度逐渐增加，辨识效果越来越差。说明最小二乘法和极大似然法抗噪声干扰的能力不足，导致拟配效果随着白噪声比例增加而变差。而差分进化算法的拟配精度在加入噪声后仍然具有较好的辨识效果，并未随着噪声比例的增加而导致拟配误差越来越大，虽然差分进化算法拟配得到的低阶系统和高阶系统的输出仍然存在一定的误差，但是差分进化算法抗噪声干扰的能力仍然要优于最小二乘法和极大似然法的抗噪声干扰能力，说明差分进化算法具有良好的鲁棒性。

本文同时也研究了平均差分进化算法的精度随着噪声比例增加的情况，得出了图12的结果。

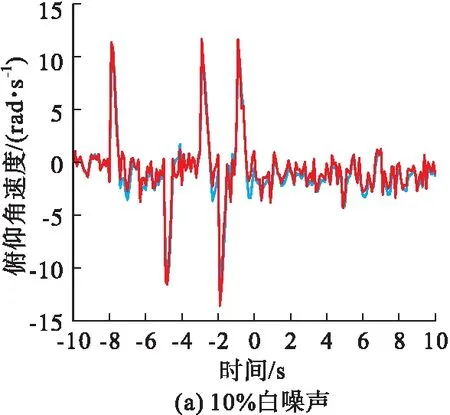
图12 加入不同白噪声后应用平均差分进化算法

通过拟配图可以看出，本文所提的平均差分进化算法加入噪声后的拟配精度仍然要高于差分进化算法的精度，噪声比例的增加并没有对拟配效果产生较大的影响，低阶系统和高阶系统的输出误差仍然较小，具有较为理想的拟配精度。说明平均差分进化算法具有良好的抗噪声干扰能力、寻优能力和鲁棒性，可以应用到工程实践中去。

3 结论

本文针对常规算法进行等效系统拟配存在的初值依赖较大，容易陷入局部最优的问题，提出了平均差分进化算法应用到等效系统拟配的新思路，得出了如下的结论：

1)仿真结果说明平均差分进化算法可以应用到等效系统拟配中,为等效系统拟配提供了一种新的方法与思路。

2)通过与最小二乘法和极大似然法进行等效系统拟配的效果进行对比，发现差分进化算法的辨识效果虽然存在一定的误差，但是拟配精度要高于最小二乘法和极大似然法的拟配精度，同时具有较好的噪声处理能力。

3)无论是理想的3-2-1-1输入还是加入噪声之后的新输入，应用本文提出的平均差分进化算法进行等效系统拟配的精度都要高于最小二乘法、极大似然法以及差分进化算法，具有较好的拟配效果，同时具有良好的噪声处理能力，对于工程实践具有较好的应用价值。