火炮控制区域问题的运动学分析与应用
韩佳佳 陶宗明 张 辉 史 博 陈 骁
(中国人民解放军陆军炮兵防空兵学院基础部,安徽 合肥 230031)
火炮是利用机械能、化学能等能量抛射炮弹,由炮身和炮架两大部分组成的射击武器[1]。图1为火炮战场作战图。战斗中,首要问题就是求出火炮的火力控制区域,并将其标绘在作战文书上[2]。当目标进入火炮控制区域时,指挥员要及时下达射击任务,保障火炮在控制区域内击中目标。
1 火炮控制区域问题分析
假设空气阻力为零,火炮发射的炮弹质心在空中运动的轨迹称为真空弹道[3]。此时炮弹只受重力作用,在空中的运动是一种抛体运动,炮弹质心的运动轨迹取决于初速度v0与发射角α。真空弹道虽不存在,但火炮在空气较为稀薄的高原地带射击,或者在空气稠密的地面附近以较小弹速射击时,可以忽略空气阻力的影响,应用真空弹道模型进行分析。

图1 火炮战场作战图
真空弹道中,由于火炮射击时初速度和发射角的不同,在竖直平面上,炮弹质心的运动轨迹是形状各异的抛物线。对于一门火炮,炮弹的初速度v0为定值的情况下,发射角α变化时所有可能的弹道曲线组成了一个曲线簇。图2为初速度v0=1000m/s的火炮以不同发射角发射炮弹时,弹道曲线在二维平面内形成的曲线簇。在曲线簇的边界,平面内存在一条每一点都与其中抛物线上的点相切的曲线,称为该曲线簇的包络线。火炮射击时的控制区域就是该包络线旋转曲面的覆盖区域。
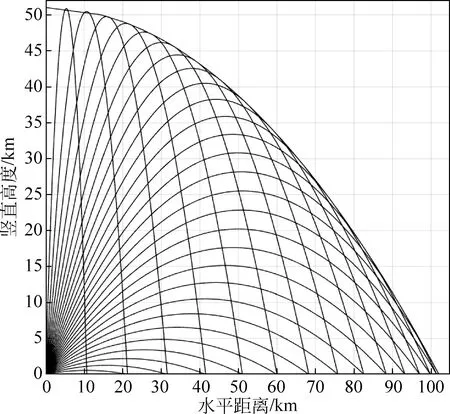
图2 曲线簇的包络线
2 分析与求解
火炮射击时,初速度为v0,发射角为α的炮弹质心运动的轨迹方程为
(1)
在火炮结构与炮弹类型不变的情况下,火炮发射炮弹的初速度v0为固定值。为便于分析炮弹质心的运动轨迹与发射角α之间的关系,根据量纲分析方法[4],可以将式(1)写为无量纲形式。取长度L和时间T为基本量,轨迹方程中各参量的量纲分别为
(2)

(3)
将上式代入炮弹质心的轨迹方程(1),可得方程的无量纲形式
(4)
真空弹道中以不同发射角发射的炮弹质心轨迹形成了一簇曲线。包络线中的每一点都在其中一条曲线上,因此包络线方程满足式(4)。并且对于控制区域内水平方向上的某一固定位置x,以不同发射角α发射的炮弹质心轨迹经过竖直方向的不同高度y,包络线上的点对应炮弹质心轨迹的最大高度。根据极值定理[5]:
(5)
由上式可得最大高度对应的发射角α:
(6)
将上式代入式(4),消去参数α,得到方程:
(7)
式(7)表示一条开口向下的抛物线。曲线簇中,火炮以任意发射角α发射的炮弹质心运动轨迹与该抛物线的交点可由以下方程组求得:
(8)
联立以上方程,得到抛物线与炮弹质心运动轨迹唯一交点为
(9)
炮弹质心运动轨迹方程(4)中该点处的斜率为
(10)
抛物线式(7)中该点处的斜率为
(11)
因此该抛物线与任意发射角α发射的炮弹质心运动轨迹相切。抛物线方程(7)为曲线簇的包络线方程。
以火炮位置为坐标原点,弹道曲线所在的平面为xOy面,炮弹飞行过程中的水平位置和竖直位置分别为x轴和y轴。根据方程(13),二维平面内火炮的控制区域是一个开口向下的抛物线,如图3(a)所示。三维空间中的火炮控制区域为该包络线的旋转曲面,其方程的无量纲形式为
(12)
在三维空间中的图形如图3(b)所示。

图3 火炮控制区域(a) 二维平面火炮控制区域; (b) 三维空间火炮控制区域
3 火炮控制区域问题在军事上的应用
3.1 间接瞄准射击发射角的范围
间接瞄准射击也称间瞄射击,是指火炮不直接瞄准目标,而是用瞄准装置赋予火炮射向和射角所进行的射击[6]。在火炮不能通视目标时,主要采用间瞄射击。此时炮阵地可以选择在障碍物后面,便于隐蔽,可达成火力突然性。

(13)
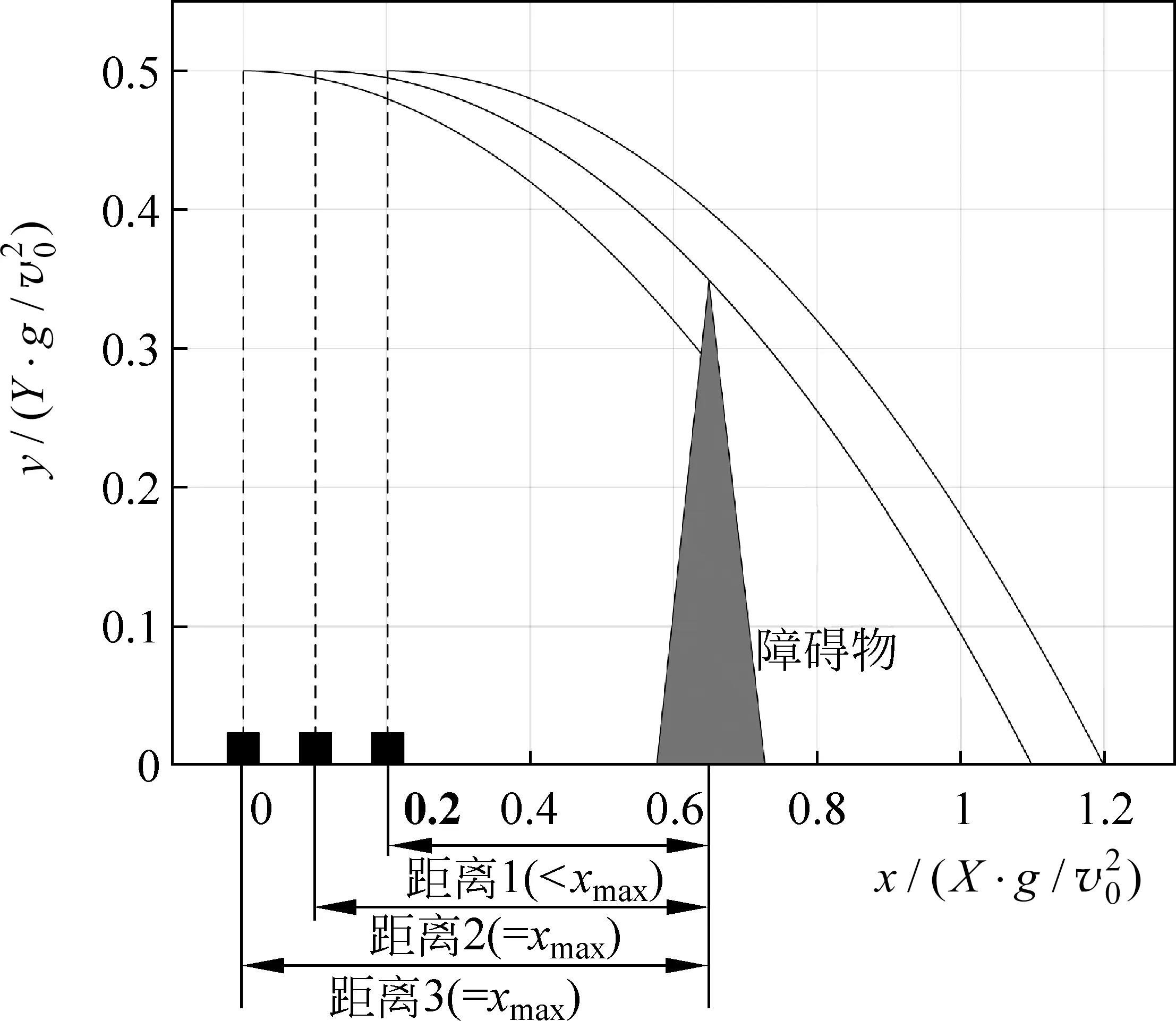
图4 火炮与障碍物的最大距离
当火炮与障碍物的距离xs (14) 上式为发射角α满足的方程,可以求出: 火炮射击时,发射角在αmin与αmax之间的炮弹都能够越过障碍物。两发射角对应的弹道曲线在障碍物后侧的交叉区域为间瞄射击时的火炮控制区域,如图5所示。 图5 火炮间瞄射击控制区域 在火炮射击过程中,如果前方有一倾角为θ的山坡(θ为正值)或洼地(θ为负值)。为保证炮弹击中目标,我方首先需要确定火炮的最大射程及最大射程所对应的发射角。 该问题可以用抛体运动的轨迹方程求解,但过程比较复杂[7],使用包络线方程能够简化求解过程。二维平面内,火炮的最大射程为包络线与山坡或洼地直线的交点,根据下列关系式: (17) 可以求出火炮最大射程所对应的坐标(x,y)为 其中,x是火炮射击目标的最远距离;y是目标的纵坐标,如图6与图7所示。由于该点在包络线 图6 火炮面向山坡射击最大射程与发射角 图7 火炮面向洼地射击最大射程与发射角 上,将式(18)代入式(11),可得最大射程所对应的发射角: (20) 在真空弹道中,火炮以不同发射角发射的炮弹都是作抛体运动后到达目标,火炮火力能够覆盖的范围为火炮控制区域。本文在对火炮不同发射角的弹道曲线进行分析的基础上,采用包络线的方法求解出火炮的控制区域,并利用数值计算的结果进行了演示。这一问题不仅为弹道学理论提供了参考,而且在军事上也有一定的应用价值。
3.2 山坡或洼地射击的最大射程与发射角
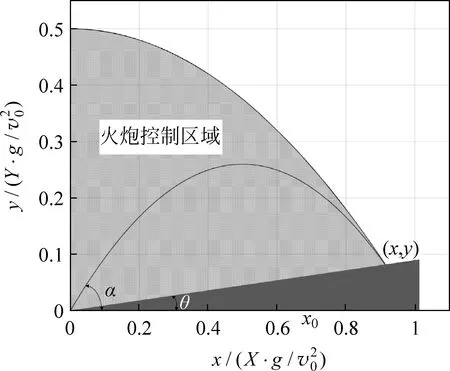
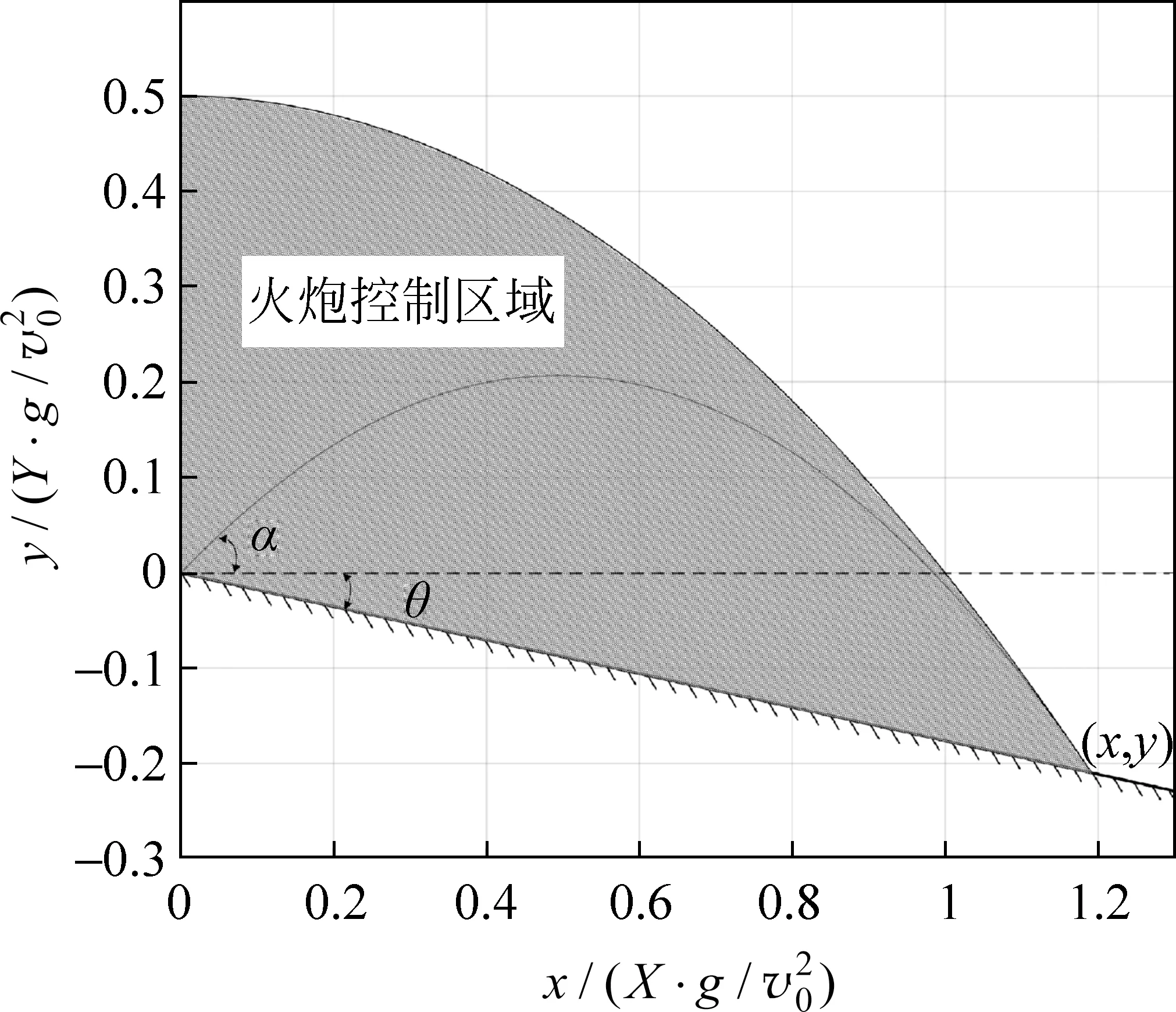
4 结语

