用于稀疏系统辨识的变步长加权零吸引最小平均p范数算法
陈思佳 赵知劲
(1.杭州电子科技大学通信工程学院,浙江杭州 310018;2.中国电子科技集团第36研究所通信系统信息控制技术国家级重点实验室,浙江嘉兴 314001)
1 引言
稀疏系统是指单位脉冲响应的零或近零值的数量远多于非零大值的系统.研究表明,稀疏系统广泛存在于现实世界中,如无线信道估计、声学回声消除、稀疏系统辨识等.稀疏系统辨识中,传统的自适应滤波算法,例如最小均方(least mean square,LMS)算法,由于没有利用稀疏特性,导致该算法性能显著退化.谷源涛教授受套索算法(least absolute shrinkage and selection operator,LASSO)[1]、压缩感知[2]等稀疏技术的启发,利用稀疏性约束,将与稀疏性有重要关联的L1范数引入LMS算法,提出零吸引最小均方(zero attracting LMS,ZA−LMS)算法[3]和加权零吸引最小均方(reweighted zero attracting LMS,RZA−LMS)算法[4].当非零权值的数量增加时,RZA−LMS 算法性能优于ZA−LMS 算法.为了在保持较快收敛速度下减小稳态误差,范涛等人提出了基于误差函数的变步长加权零吸引最小均方(variable step size RZA−LMS,VSS−RZA−LMS)算法[5].为了解决块稀疏系统辨识问题,Yan 提出了块稀疏加权零吸引归一化LMS(block sparse reweighted zero attracting normalized LMS,BS−RZA−NLMS)算法[6].针对输入信号频谱动态范围较大时,闫震海将加权的L1范数应用到改进的多带结构子带自适应滤波(improved multibandstructured subband adaptive filter,IMSAF)算法中,提出了基于加权L1范数约束的改进的多带结构子带自适应滤波(L1−reweighted improved multiband-structured subband adaptive filter,L1−RIMSAF)算法[7].
在实际系统中,常伴有显著脉冲特性的噪声,这些脉冲噪声有来自于自然环境的,也有来自人造设备的.α稳定分布模型可以很好地描述这类噪声[8].由于上述算法在脉冲噪声下的性能严重退化,Nikias等人用误差函数的p范数(分散系数的带噪估计)取代平方误差函数,提出了最小平均p范数(least meanp-norm,LMP)算法[9];芦璐等人提出了鲁棒扩散型归一化LMP(robust diffusion normalized LMP,RDNLMP)算法[10],周琳将零吸引思想应用到LMP算法中,提出了零吸引最小平均p范数(zero attracting LMP,ZA−LMP)算法[11].与ZA−LMS算法相比,ZA−LMP算法虽然提高了稳态性能,但收敛速度大大降低.
ZA−LMP算法的零吸引项对所有单位脉冲响应施以相同的吸引力,不能辨别零与非零值.针对该问题,本文将加权零吸引思想引入到LMP算法中,提出了加权零吸引最小平均p范数(reweighted zero attracting LMP,RZA−LMP)算法;为了在保持较快收敛速度下进一步减小稳态误差,将基于无噪先验误差的变步长思想应用到RZA−LMP算法中,提出了变步长零吸引最小平均p范数改进(improved variable stepsize RZA−LMP,IVSS−RZA−LMP)算法.在迭代初期,该算法的无噪先验误差功率较大,因此使用较大的步长;随着无噪先验误差功率减小,步长也相应减小;当达到稳态时,权重矢量不再随机调整.
2 加权零吸引最小平均p范数算法
本文以稀疏系统(单位脉冲响应稀疏)的自适应辨识为背景,系统辨识框图如图1所示.令未知系统的有限长单位脉冲响应和输入信号分别为

其中L为脉冲响应长度.未知系统的输出为
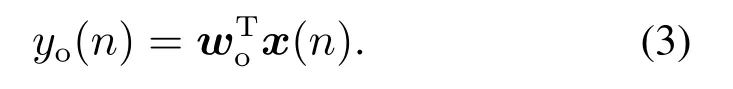
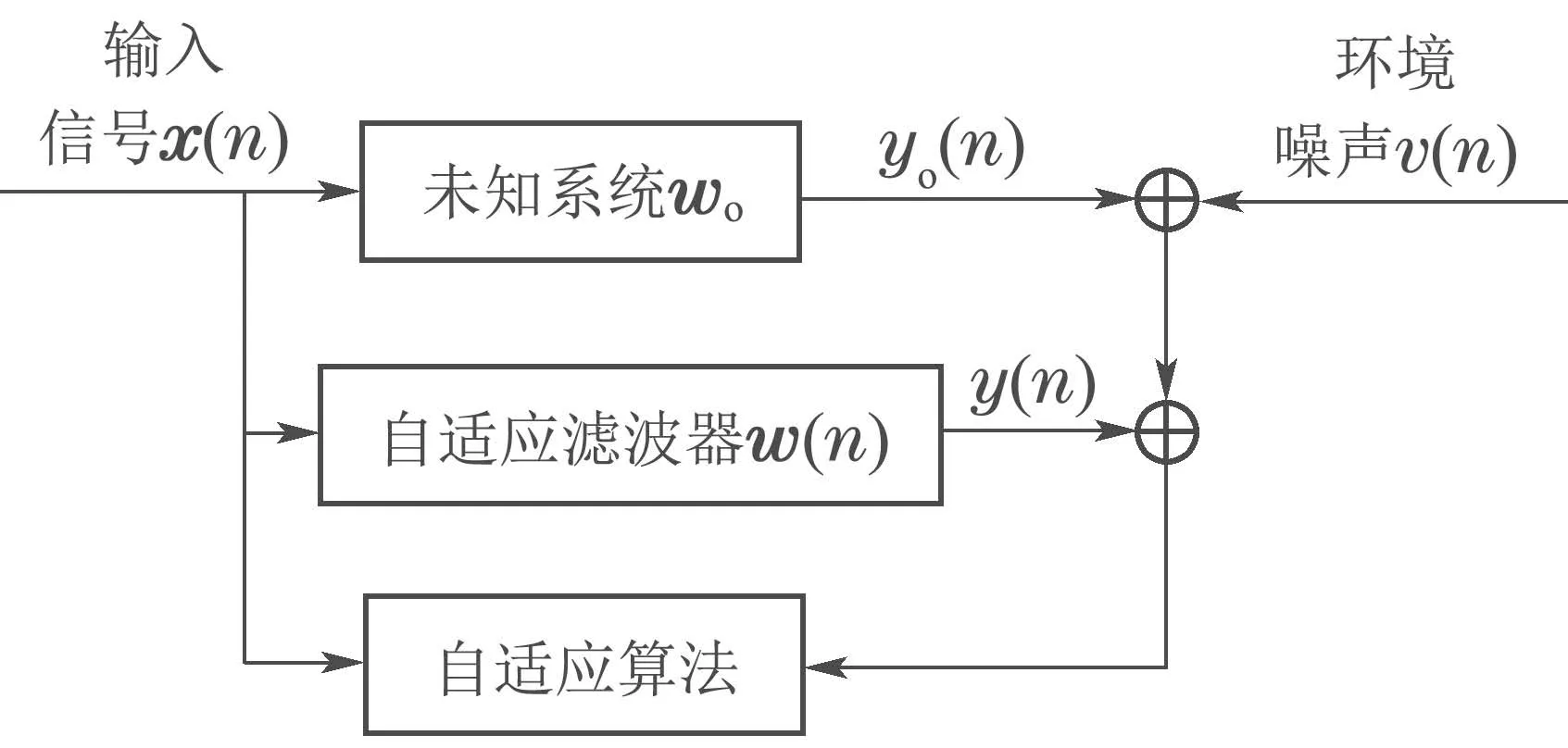
图1 系统辨识框图Fig.1 System identification block diagram
系统输出yo(n)受到α稳定分布的环境噪声v(n)干扰.自适应滤波器的期望输出为

当x(n)通过权重矢量为w(n)的自适应滤波器,得到其输出信号为

其中:x(n−i+1)表示输入信号x(n)中的第i个分量;wi(n)表示第n次更新得到的权值矢量w(n)的第i个分量.误差信号为

自适应滤波器自适应地调整权重矢量w(n),使其趋近于wo从而达到系统辨识的目的.
在α稳定分布噪声背景下,选择代价函数为J=E[|e(n)|p],利用随机梯度下降法可得LMP算法的权重矢量w(n)更新公式[9]为

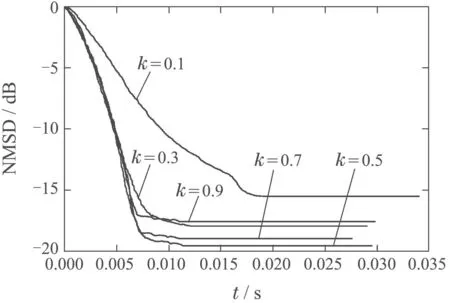
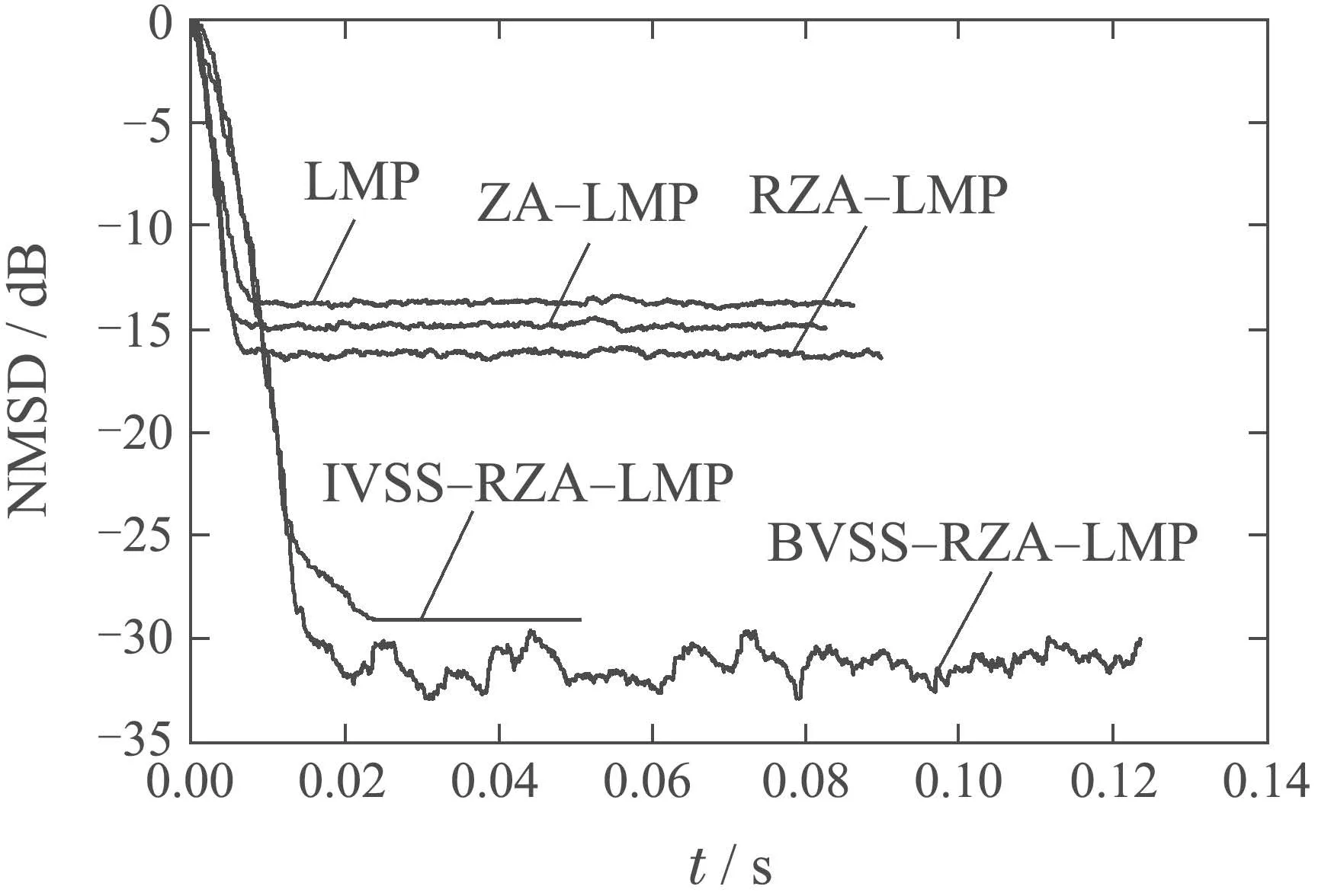
其中:µ是步长且0<µ<1;p为范数中的指数变量,且0 在稀疏系统中,引入加权零吸引[4]思想,得到RZA−LMP算法的代价函数为 其中:γRZA为非负的平衡因子,ε为一个非负的常数.同理,利用随机梯度下降法,得到权重矢量更新公式: 其中ρ为零吸引控制因子,控制零吸引力的大小,其值为这就是本文提出的RZA−LMP算法. 由式(9)可以看出,RZA−LMP算法通过事先设定阈值ε对权重矢量的零和非零系数加以区分[4],根据系数值的大小施加不同的吸引力.当|wi(n)|ε时,认为该系数为零系数,因此RZA−LMP算法对其施以较大的吸引力,使其快速收敛.当|wi(n)|≫ε时,认为该系数为非零系数,则RZA−LMP算法对这些系数的收敛影响有限. 固定步长的自适应滤波算法不能同时获得较小的稳态误差和较快的收敛速度[12].为了解决这一问题,将基于误差函数的变步长方法[5](本文称为变步长基本方法)应用到RZA−LMP算法中;步长函数计算如下: 无噪先验误差ef(n)是指将环境噪声v(n)剔除之后的估计误差值: 无噪先验误差功率为 将式(10)的S(n)代替式(9)的µ,得到VSS–RZA–LMP基本算法(简记为BVSS−RZA−LMP)的权重矢量更新公式为 当变步长函数S(n)满足[15] BVSS−RZA−LMP算法的权重矢量w(n)一定收敛. 由BVSS−RZA−LMP算法可见,随着迭代进行,权重矢量一直在调整,且具有随机性;然而当达到稳态时,希望权重矢量做微小甚至不调整;因此,本文提出一种变步长方法,其步长函数计算如下: 其中k为无噪先验误差功率因子.改进算法的主要思想是当无噪先验误差功率大于阈值c时,利用式(19)的步长函数S(n)和式(16)更新权重矢量;当小于等于阈值c时,权重矢量不再调整,即 由此得到本文提出的VSS−RZA−LMP改进算法(简记为IVSS−RZA−LMP),具体算法步骤如下: 步骤1选择合适的参数,初始化w(0)=0,rex(0)=0, 步骤2计算e(n)=d(n)−wT(n −1)x(n); 步骤3由式(13)−(15)计算 步骤4若(n)>c,由式(19)计算步长S(n),然后根据式(16)更新权重矢量w(n); 步骤5否则,根据式(20)更新权重矢量w(n). 表1给出了RZA–LMP,BVSS–RZA–LMP和IVSS–RZA–LMP三种算法在第n次迭代时的迭代步骤,以及所需的乘加次数.第n次迭代时,利用式(21)所示的归一化均方偏差(normalized mean square deviation,NMSD)[5]对算法的收敛性能和稳态性能进行评估,其值越小,说明系统辨识越准确. 表中:N0为3种算法的NMSD值分别达到收敛状态的迭代次数,L为稀疏系统的脉冲响应长度. 由表1可知,因为稀疏系统的脉冲响应长度L为常数,所以在迭代次数为N时,IVSS−RZA−LMP算法的计算复杂度为O(N). 表1 3种算法的计算复杂度Table 1 Computational complexity of the three algorithms 本文将BVSS−RZA–LMP和IVSS−RZA–LMP算法应用于线性稀疏系统辨识,该稀疏系统的单位脉冲响应序列为有限长,且大部分单位脉冲响应序列值为零.利用稀疏度[16]衡量系统的稀疏性. MATLAB是一种高级的矩阵语言,提供了大量的内置函数,操作简单高效,从而广泛地应用于信号处理领域.本文首先利用MATLAB仿真构造一个线性稀疏系统,选择稀疏系统的脉冲响应长度L=110,稀疏度为.然后,在MATLAB 环境下编程实现BVSS–RZA–LMP和IVSS–RZA–LMP两种算法.实验中,输入信号x(n)是均值为0、方差为1的高斯随机信号;观测噪声v(n)为α稳定分布噪声,其各参数分别设置为对称系数β=0、位置参数a=0、特征指数α=1.5、分散系数γ=0.002.设置信噪比SNR=2 dB;迭代次数N=6000;各算法的范数p均为1.15.所有仿真曲线都是100次蒙特卡洛仿真结果的平均. 实验1α稳定分布噪声背景下ZA−LMS,RZA–LMS,ZA−LMP,RZA−LMP算法的性能比较.4种算法的固定步长µ=0.01,ZA−LMS和ZA−LMP算法的零吸引控制因子ρ=1.5×10−4;RZA−LMS 和RZA−LMP算法的零吸引控制因子ρ=7×10−4,加权零吸引阈值ε=0.05,得到4种算法的NMSD曲线如图2所示. 由图2可见,在α稳定分布噪声背景下,当步长相等时,ZA−LMP和RZA−LMP 算法的稳态误差分别为−13.04 dB和−14.33 dB;而ZA–LMS和RZA–LMS算法的稳态误差因波动剧烈无法准确得到.综上可得,RZA–LMP算法性能最好,ZA–LMP算法次之,RZA–LMS和ZA−LMS算法的性能均较差. 图2 4种算法的性能比较Fig.2 Performance comparison of the four algorithms 实验2α稳定分布噪声背景下无噪先验误差功率因子k对IVSS–RZA–LMP算法的影响.IVSS–RZA–LMP算法的变步长系数η=0.01,零吸引控制因子ρ=7×10−4,加权零吸引阈值ε=0.05,指数权重因子λ=0.97,δ=1×10−6,无噪先验误差功率阈值c=0.3.无噪先验误差功率因子k的取值范围从0.1至0.9,间隔为0.2,得到IVSS−RZA−LMP 算法的NMSD曲线如图3所示. 图3 不同k下IVSS−RZA−LMP算法的NMSD曲线Fig.3 NMSD curve of IVSS−RZA−LMP algorithm under different k 由图3 可知,在无噪先验误差功率因子k分别为0.1,0.3,0.5,0.7 和0.9 时,IVSS−RZA−LMP 算法收敛时的NMSD 值分别为−15.11 dB,−20.25 dB,−22.12 dB,−21.0 dB 和−19.4 dB,且NMSD 达到收敛所需的时间分别为0.03326 s,0.01728 s,0.01650 s,0.01562 s和0.01678 s.因此可得,当无噪先验误差功率因子k=0.5时,IVSS−RZA−LMP算法能够在相对较短的时间内达到最小的NMSD值.下文仿真取k=0.5. 实验3α稳定分布噪声背景下无噪先验误差功率阈值c对IVSS–RZA–LMP算法的影响.IVSS–RZA–LMP算法的无噪先验误差功率阈值c分别取0.05,0.1,0.2,0.3,0.4,其他各参数同实验2,得到IVSS−RZA−LMP算法的NMSD曲线如图4所示. 由图4可知,无噪先验误差功率阈值c的值越小,IVSS−RZA−LMP算法收敛所需的时间越长,α稳态误差越小;但当阈值c过小时,该算法收敛后的稳定性降低.这是因为是将环境噪声剔除之后的估计误差功率,越小,则表示IVSS−RZA−LMP算法的权重矢量w(n)离最优值wo越近,当小于等于阈值c时,IVSS−RZA−LMP算法认为此时已经达到了稳态,因此权重矢量w(n)不再更新.然而,当阈值c过小时,该算法在到达稳态一段时间内仍继续更新权重矢量,即w(n)继续随机波动,相应地,也随机波动,从而使变步长S(n)随机波动,这导致IVSS−RZA−LMP算法收敛后的稳定性较差.综上所述,选择合适的无噪先验误差功率阈值c能够保证IVSS−RZA−LMP算法收敛后的稳定性,根据图4的仿真结果可得,当c=0.1时,IVSS−RZA−LMP算法的稳态误差较小且稳定性较好.下文仿真取c=0.1. 图4 不同c下IVSS−RZA−LMP算法的NMSD曲线Fig.4 NMSD curve of IVSS−RZA−LMP algorithm under different c 实验4α稳定分布噪声背景下LMP,ZA−LMP,RZA–LMP,BVSS–RZA–LMP,IVSS–RZA–LMP算法的性能比较.5种算法的参数设置如表2所示,得到5种算法的NMSD曲线如图5所示. 表2 5种算法参数Table 2 Parameters of the five algorithms 图5 5种算法的性能比较Fig.5 Performance comparison of the five algorithms 由 图5 可 知,LMP,ZA−LMP,RZA−LMP,IVSS−RZA–LMP 算法的稳态误差分别为−12.76 dB,−13.94 dB,−15.38 dB 和−30.18 dB,BVSS−RZA−LMP 算法的稳态误差波动大,其值不确定.LMP,ZA−LMP,RZA−LMP算法达到稳态所需的时间分别为0.0094 s,0.0097 s,0.0101 s;IVSS−RZA−LMP算法的NMSD达到LMP,ZA−LMP,RZA−LMP稳态NMSD 值所需时间分别为0.0085 s,0.0089 s,0.0094 s,与其他3 种算法的时间相当;因此,在5 种算法中,IVSS−RZA−LMP算法在较快收敛的同时能够获得最小的稳态误差,性能最好,BVSS−RZA−LMP算法因稳态性能差而不适用. 实验5α稳定分布噪声背景下,不同稀疏度下的LMP,ZA–LMP,RZA–LMP,IVSS–RZA–LMP算法性能比较.各算法参数同实验4.分别取稀疏度为,4种算法的仿真结果分别如图6(a)和6(b)所示. 图6 不同稀疏度下4种算法性能比较Fig.6 Performance comparison of the four algorithms with different sparsity 由图6可以看出,随着系统稀疏度的增加,IVSS−RZA−LMP算法一直保持着最低的稳态误差.当系统较稀疏时(稀疏度为,IVSS−RZA−LMP 算法的NMSD 达到LMP,ZA–LMP和RZA−LMP稳态NMSD值所需时间几乎相同;当系统稀疏度增大时,前者所需时间有所增加. 针对α稳定分布噪声下,稀疏系统中自适应算法无法在收敛速度较快时获得较小的稳态误差的问题,本文提出变步长加权零吸引最小平均p范数基本(BVSS−RZA−LMP)算法和变步长加权零吸引最小平均p范数改进(IVSS−RZA−LMP)算法.系统辨识的仿真结果表明,在α稳定分布噪声下,BVSS−RZA−LMP算法因稳态性能较差而不适用;IVSS−RZA−LMP算法在系统稀疏度较小时,能够同时获得较小的稳态误差和较快的收敛速度,且具有较好的稳态性能.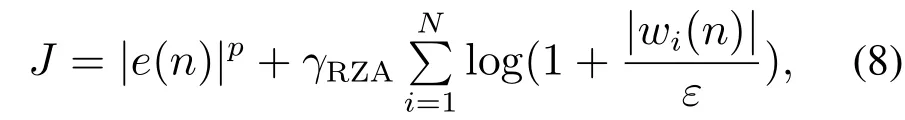

3 变步长加权零吸引最小平均p 范数(VSS−RZA−LMP)算法
3.1 VSS−RZA−LMP基本算法







3.2 VSS−RZA−LMP改进算法


3.3 复杂度分析
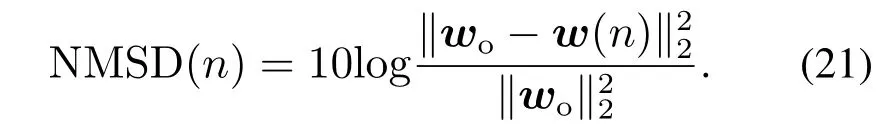

4 算法仿真与性能分析
4.1 仿真背景
4.2 仿真结果分析




5 结束语

