模糊需求下时间依赖型车辆路径优化

范厚明,李 荡,孔 靓,任晓雪

(大连海事大学交通运输工程学院,辽宁大连 116026)

1 引言

车辆路径问题(vehicle routing problem,VRP)由Dantzig[1]于1959年提出,属于经典的NP–hard问题,自提出以来,成为运筹学和组合优化领域的前沿研究热点问题.随着现代物流的发展,城市交通负载日益繁重,传统的VRP模型难以满足快捷、高效的配送要求.为此一些学者基于现实中出现的不同情况对VRP问题进行了拓展研究,使其不断贴近实际,如有顾客访问时间窗限制的带时间窗的车辆路径问题(vehicle routing problem with time windows,VRPTW)、考虑了客户需求不确定的模糊需求车辆路径问题(vehicle routing problem with fuzzy demand,VRPFD)、车辆行驶速度变化的时间依赖型车辆路径问题(time dependent vehicle routing problem,TDVRP)等.本文研究的客户需求模糊且有时间窗约束的时间依赖型车辆路径问题(time dependent vehicle routing problem with fuzzy demand and time windows,TDVRPFDTW)是VRPTW,TDVRP,VRPFD3者的集成,更符合现实路网环境及配送要求,针对该问题的研究具有重要的理论与实际意义.

VRPTW出现较早,已有较多、较成熟的研究.而有关VRPFD问题,现有文献多应用模糊集可能性、可信性等理论界定模糊需求变量和相关约束.Goncalves等[2]基于可信性理论,通过建立模糊机会补偿模型,用模糊模拟和智能算法来求解带时间窗的VRPFD;曹二保等[3]针对VRPFD问题,建立基于模糊可信性理论的模糊机会约束规划模型,并提出求解该问题的一种基于随机模拟的混合差分进化算法;Cao等[4]构建模糊机会约束规划模型对开放式的多中心VRPFD进行了研究,利用随机模拟和改进的差分进化算法求解;Kuo等[5]以垃圾收集系统为研究对象,运用基于遗传算法的混合粒子群算法求解VRPFD;王君等[6]针对具有模糊顾客需求的带时间窗车辆路径问题,提出了管理车辆服务模糊需求的动态优化策略,设计了嵌入模糊模拟的改进非支配排序混合遗传算法来求解模型;张建勇等[7]通过引入决策者主观偏好值的概念,建立了模糊机会规划模型,提出了一种基于模糊模拟的混合遗传算法;Shi等[8]考虑了具有模糊需求的家庭医疗药物的调度问题,构建模糊机会约束模型,提出了一种混合遗传算法与随机模拟方法相结合的求解方法;Chang-Shi等[9]设计混合蚁群算法求解VRPFD,并提出一种双车对环协调策略以减少额外成本.张晓楠等[10]设计混合分散搜索和变邻域搜索的变邻域分散搜索算法求解VRPFD,并提出一种新的失败点返回策略.李阳等[11]基于先预优化后重调度的思想,提出一种两阶段变邻域禁忌搜索算法对其求解,并在重调度阶段提出一种新的点重调度策略对预优化方案进行调整.

有关TDVRP的研究,Hu等[12]针对客户时间窗和车辆旅行时间不确定的车辆路径问题,提出了一种鲁棒优化模型,并设计了一种基于改进的自适应变邻域搜索启发式的两阶段算法求解;Balseiro等[13]提出一种混合的插入启发式蚁群算法来求解带时间窗的TDVRP;Deng等[14]对带时间窗的TDVRP,提出了一种混合蚁群算法和最大最小蚁群算法的多蚂蚁系统算法求解;段征宇等[15]使用“最大–最小蚂蚁系统”改进蚁群系统求解TDVRP;Kuo等[16]提出关于TDVRP的一种总油耗计算模型,并设计了串行模拟退火算法,寻找碳排放量最少的路径;吴瑶等[17]考虑路网的时变特性,研究易腐食品的生产–配送问题,建立了以系统总成本为目标的优化模型,并设计混合遗传算法求解;穆东等[18]提出一种并行的模拟退火算法求解TDVRP,提高了传统串行模拟退火算法求解TDVRP的效率;Figliozzi[19]改进了Solomon测试数据库,设计了Figliozzi测试数据库,用于对求解TDVRP的不同算法进行对比.

通过梳理已有文献可见,现有研究还存在以下不足:1)现有针对VRPFD文献多为求解算法的创新以及服务失败后返回策略的研究,虽然有文献[2,7]综合考虑了客户模糊需求和时间窗的约束,但也都只考虑了车辆行驶速度不变的情况,忽视了天气变化、高峰时段、突发事件等因素对交通状况的影响,从而导致基于速度恒定的VRPFD模型不能准确的反应和解决实际问题;2)现有针对TDVRP的研究,虽然大多考虑了客户时间窗的约束,且分别提出不同的求解算法,但目前的研究基本都视客户的需求是已知的、确定的,没有考虑现实生活中客户的需求的模糊性和不确定性.针对以上不足,本文以TDVRPFD为研究对象,并考虑客户时间窗的约束,首先基于模糊可信性理论构建模糊机会约束规划模型,并设计自适应大规模邻域搜索算法对其求解,然后针对预优化路径的失败点及其后续点进行重调度,有效降低由于客户需求模糊影响导致的配送路径额外成本,为合理的选择配送方案提供理论依据.

2 问题描述及模型建立

2.1 问题描述

本文所研究的TDVRPFDTW可描述为在一个完备的有向图G=(V,E)中,V={0}∪V0,V0={1,2,…,n}为客户点的集合;0表示配送中心,配送中心能够满足所有客户需求.E={(i,j)|i,j∈V}表示边的集合,其中(i,j)表示客户i和客户j之间的边,其路径成本为cij.配送中心配有m台车型相同的车辆,车辆的最大载重重量为Q,用K={1,2,…,m}表示车辆集合.每个客户的需求量在配送前是不确定的,用三角模糊数来表示.T0jk表示车k从配送中心的出发时刻,为车辆k到达客户i的时刻,表示车辆k在客户i的开始服务时刻,tsi表示配送车辆在客户i的服务时间,表示车辆k离开客户i的时刻,tijk表示车辆k从客户i到j的行驶时间.客户i(i∈V0)的需求必须在时间窗[ETi,LTi]内满足,ETi为客户i的最早可接受服务时刻,LTi为客户i的最迟可接受服务时刻.如果早于ETi,则车辆k在客户i处等待,等待时间否则,

决策变量xijk表示车辆k是否从i行驶到j,若是,则xijk=1,否则为0;yjk表示客户j是否由车辆k服务,若是,则yjk=1,否则为0.

2.2 速度时间依赖函数表示

本文采用Ichoua[20]速度时间依赖函数表示动态路网,Ichoua的时间依赖行驶函数如下图1所示,把路段的旅行速度表示为分段函数形式,如图1(a),由此得到连续的路段行程时间函数,如图1(b),使得路网满足先入先出(first in first out,FIFO)准则.

图1 Ichoua时间依赖行驶函数Fig.1 Time dependent driving function of Ichoua

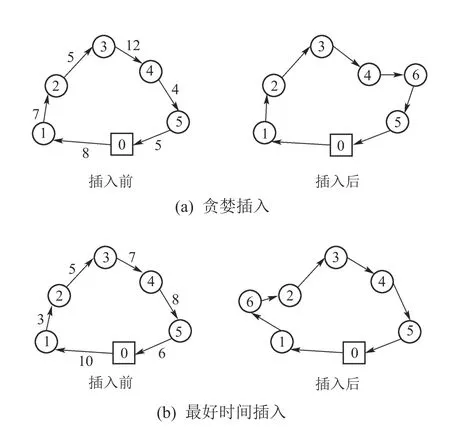
首先将配送中心每天的工作时间分为P个时间段,假设配送车辆从i的出发时刻在第p(p∈[1,P])个时段内,第p个时间段的开始和结束时刻分别为[Tp,Tp+1],该时段的行驶速度为vp,客户i到客户j的距离为dij.配送车辆从i行驶到j,存在跨时段和不跨时段两种可能性,若此时配送车辆在出发的第一个时间段内就从客户i到达客户j,车辆无需跨时段行驶;否则配送车辆需跨时段行驶,假设车辆从i到j需跨C(C

2.3 模糊需求度量

预优化阶段,假设车辆k按客户序列{a,b,c,e}服务,车辆从配送中心满载出发,满载装货量为Q,每个客户的需求均由三角模糊数表征.车辆服务完客户a,b,c后的实际剩余装载量为

由于客户a,b,c的需求量为三角模糊数,可知服务完c后的剩余车载量也为三角模糊数,

基于可信性理论,当车辆k继续对下一客户e服务时,客户e的需求量小于剩余车载量的可信度为

2.4 建立数学模型

在路网速度时变的条件下,同一配送车辆在相同的配送路线中,若不考虑客户的时间窗约束,则配送时间随路网的速度变化而变化,但有时间窗约束时,当配送车辆提前到达客户点,也需要原地等待,这虽然缩短了车辆的行驶时间,但增加了等待时间,两种情况下车辆离开路线中最后一个客户点的时间相同.因此,本文以车辆行驶距离最短为目标,在预优化阶段,对于给定的决策者偏好值α,相应的预优化模型如下:

其中:目标函数(3)为最小化路径成本;式(4)保证每个客户有且仅有一条车辆路径对其服务,同时还表示车辆的进出平衡约束;式(5)表示同一客户无路径连通;式(6)表示每辆车仅有一条服务路径,且从配送中心出发,配送完后要返回配送中心;式(7)–(8)保证客户点被车辆服务时一定有路径与其连接;式(9)为支路消除约束,S为车辆k的服务路线客户集合;式(10)–(11)表示车辆出发或返回配送中心要满足配送中心的时间窗要求,式中ET0,LT0分别为配送中心的最早开始服务时间和最晚结束服务时间.式(12)保证了客户的开始服务时刻必须满足客户间的行驶时间;式(13)为模糊容量机会约束,保证车辆在选择点进行服务的时候,其需求量不大于Q的可信度高于预先设定的置信水平;式(14)–(15)保证车辆的开始服务时刻必须满足顾客的时间窗约束;式(16)–(17)为决策变量属性.

步骤2根据式(1)分别求得从当前节点出发到所有未访问节点的到达时间,从到达时间满足时间窗要求的未访问客户集中选择开始时间最小的一个节点插入到当前路径中.若所有未插入客户的到达时间都不在时间窗内,则选择到达时间距最早开始时间最近的一个节点插入到当前路径中.

步骤3重复步骤2,若已达到当前车辆的容量约束,则重新派一辆车,若所有的节点都已访问,则结束计算.

3 求解TDVRPFDTW的ALNS算法

VRP问题属于经典的NP–hard问题,本文研究的TDVRPFDTW问题考虑了时间窗,客户需求不确定及旅行速度变化等因素的影响,求解更为复杂.自适应的大规模邻域搜索算法(adaptive large neighborhood search algorithm,ALNS)在求解VRP问题时既能保持大规模邻域搜索的寻优能力,又能克服低效耗时的弱点,可在有限的时间范围内最大程度的遍历客户.故本文设计了ALNS算法对TDVRPFDTW问题进行预优化和重调度两阶段求解,在求解的预优化方案中,由于客户点需求是模糊的,重调度阶段先采用随机模拟算法(stochastic simulation algorithm,SSA)对模糊需求进行确定模拟,然后对预优化方案的服务失败点进行重调度求解,得到最终方案.

3.1 ALNS算法框架

ALNS算法依据毁坏重建的原则,通过在每个迭代过程中摧毁和重建部分方案来逐步得到更好的方案.在这个不断扩展解决方案邻域的过程中,每个摧毁和重建因子会成对出现,且都被赋予一定的权重,其被选择的概率与其权重息息相关.本文设计的ALNS算法流程如图2所示.

3.2 ALNS算法设计

1)生成初始解.

本文依据最近邻算法的思想生成初始解,具体步骤如下:

步骤1于给定的出发时间,在可用车辆中选配一辆车,从配送中心出发;

图2 ALNS流程图Fig.2 The basic flow of ALNS

2)启发式算子.

在每次迭代中,当前解中的µ个客户通过移除启发式算子删除,然后又通过插入启发式算子构造新的解.µ为控制邻域大小的参数,随着µ的增大,搜索邻域也会变得更大,也就意味着找到最优解的可能性就越大.本文采用3种移除启发式算子和两种插入启发式算子.

a)移除启发式算子.

①随机移除启发式算子.

随机移除启发式算子是指在每次迭代中,随机选取当前解中的µ个客户进行删除.

②最远距离移除启发式算子.

最远距离移除启发式算子是选择距离成本最高的客户删除.在每次迭代中,计算所有路径中所有客户的距离成本,选取距离成本最大的µ个客户删除.客户j的距离成本为D(j)=|dij+djk|,dij为j与其紧前节点i的距离,djk为j与其紧后节点k的距离.具体操作如图3(a)所示,图中数值为客户之间的距离.

③最差时间移除启发式算子.

最差时间移除启发式算子是选取时间偏差最大的客户从当前路径中删除,客户j的时间偏差WT(j)=|yj −aj|,式中yj为配送车辆到达客户j的时间,aj为客户j的最早可接受服务时间.具体操作如图3(b)所示,图中括号内的数据为配送车辆到达客户的时间和客户的最早接受服务时间.

图3 移除操作示意图Fig.3 Examples of removal operation

b)插入启发式算子.

①贪婪插入启发式算子.

贪婪插入启发式算子是将移除列表中的每一个客户i以最小的插入成本插入到路径中,在时间窗的约束下,计算其所有可行插入位置的插入成本,客户i的插入成本C(i)=dji+dik −djk,式中j为插入位置的前序点客户,k为插入位置的后续点客户,这也就是相当于以最小插入成本插入客户.具体操作如图4(a)所示,客户之间的数值为被插入客户在各位置的插入成本C.

②最好时间插入启发式算子.

对于待重建解中的每一条子路径,在时间窗的约束条件下,首先找出客户j的所有可行插入位置并计算插入后的时间偏差量,客户j的时间偏差量BT(j)=|yj −aj|,式中:yj为配送车辆到达客户j的时间,aj为客户j的最早可接受服务时间,然后将客户j插入在时间偏差量最小的位置.具体操作如图4(b)所示,客户之间的数值为被插入客户在插入各位置后的时间偏差量BT.

图4 插入操作示意图Fig.4 Examples of insertion operation

3)自适应调整机制.

本文采用轮盘赌来确定每一次迭代中选择的移除或插入启发式算子.ρi表示每次迭代中移除启发式算子hi(或插入启发式算子)的权重,初始值设为1,则在m个启发式中,启发式算子hi被选择的概率可表示为搜索过程分为若干段完成,每一段由φ个连续的迭代过程组成,在每一段的迭代结束后,根据记录的启发式算子性能调整所有的权重ρi.

定义πi为启发式算子hi在当前段所获得的评价总分数,在每段的迭代之前πi的值设置为0,启发式算子hi的得分πi由参数σ1,σ2,σ3所决定.若迭代之后的新解为全局最优解,则此次迭代所用到的启发式算子得分为σ1;若新的解代表的路径之前没有访问过,且这个新解比当前解优,则启发式算子得分为σ2;若新的解代表的路径之前没有访问过,且这个新解比当前解差,但此新解被接受,则启发式算子得分为σ3.λi表示启发式算子hi在当前段中迭代应用的次数,若λi >0,则每段迭代结束后ρi更新,

η为控制参数,η∈[0,1].若λi=0,则在下一段的迭代中ρi保持不变.

4)劣解接受标准和迭代终止条件.

为了避免陷入局部最优,本文依据模拟退火算法设计劣解接受标准和迭代终止准则.通过对当前解S中的客户进行移除和插入重建的操作,产生新解St,如果obj(St)

温度T从每次迭代的初始温度Tstar开始,在每次迭代中,温度T的冷却速率为τ(0<τ <1),在温度达到临界值后停止迭代.

3.3 重调度策略

在实际操作中,即使预优化方案中车辆装载量满足所有客户点可信度检验,也是有可能出现客户点需求量超出车辆剩余装载量的情况,此时该客户点为服务失败点,该路线上失败点及后续客户都不能被服务,此时就要执行点返回策略来进行路线调整,由于路径失败导致的相关超出预优方案部分配送路径所增加的费用称为额外费用.

1)随机模拟算法.

假定只有配送车辆到达客户点进行服务时,客户点的模糊需求量才得以明确,在算法中通过随机模拟算法(SSA)模拟客户点需求量来确定失败点.在给定模糊需求数[d1i,d3i]中生成一个随机数d,并计算其隶属度µ(d),再生成一个[0,1]范围内的随机数ε,比较µ(d)和ε,若εµ(d),则客户i的实际需求量为d,否则重新生成d和ε,直至满足εµ(d)为止.

2)重调度.

针对失败点所导致的服务失败问题,现有文献多采用点返回策略进行处理.如图5的简单例子所示,图5(a)为预优化路径,图5(b)失败点返回,图5(c)失败前点返回,图5(d)失败前序点返回3种方式,其中图5(b)属于失败点返回补货策略,图5(c)–5(d)属于预先补货策略.

图5 失败点返回策略示意图Fig.5 Examples of failure point return policy

由三角形三边原理可知,预补货策略明显优于失败点返回补货策略,但难以确定预补货策略的最优返回点,在后续客户需求不明确时难免出现不当返回,从而增加额外成本.因此本文采用重调度策略,重调度策略在文献[11]中的应用证明了其可获得更好的调整方案,具体调度过程如下:

首先进行失败点及后续点的确认.先对预优化方案中路线逐条进行模拟,确认失败点及后续点,车辆在失败位置允许进行部分服务,随后返回配送中心,本路径配送结束,所有的失败点及后续点组成待重调度客户点集合VR={1,2,…,r},VR⊂V0,此时VR中仅有失败点的需求确定,后续点的需求仍为模糊.若VR为空集,则表明预优化方案合理,路径中客户点模糊需求不超出配送车辆能力,无需重调度.

然后进行客户点的重调度.第2阶段重调度策略求解的同样是TDVRPFDTW,但问题规模相对较小.在重调度阶段,决策者风险偏好值β水平设置较高,一般βα,与预优化阶段相同,重调度路径中客户点处同样要进行可信性检验,在重调度路径中也可能会出现失败点,此时算法采取失败点返回策略,重调度路径优化后对其进行模拟,客户点需求量仍通过SSA确认.重调度阶段客户规模较小,因此重调度路径中服务失败的概率较小.

4 算例验证及结果分析

采用MATLAB 2016b编译算法在PC机上运行,电脑操作系统为Window 7,运行内存大小为8 GB,CPU为4核酷睿i7–7500,主频为3.4 GHz.经过反复地试验,ALNS算法参数设定如下:初始温度Tstart=100,温度下降速率τ=0.99,邻域规模µ=20,每一小段的迭代次数φ=50,启发式算子评价参数σ1=100,σ2=20,σ3=10,控制参数η=0.5;本文启发式算法迭代代数设置为1000代.

表1 Figliozzi速度时间依赖函数Table 1 Speed time dependent function of Figliozzi

本文测试算例来自于Figliozzi[19]提供的标准测试算例,Figliozzi测试数据库是在Solomon提供的标准测试算例的基础上增加了4组时间依赖函数.Dr.Solomon 提供的测试数据库下载:http://w.cba.neu.edu/∼msolomon/problems.htm.Figliozzi将一天的工作时间均匀地分为5等份,分别为[0,0.2T),[0.2T,0.4T),[0.4T,0.6T),[0.6T,0.8T),[0.8T,T],并假设一天存在早高峰和晚高峰,因此设置4组时间依赖函数如表1所示.

4.1 需求确定型算例验证

目前关于TDVRPFDTW没有标准的算例,为验证算法的性能,首先使用Figliozzi数据库C1类算例集求解需求确定的TDVRPTW,计算结果如表2–3所示,该结果包括车辆路径成本和路线所需车辆数两部分,TD为路径成本,N表示路线所需车辆数,表2中Best为目前国际上公布的最优解.

车辆速度恒定时,表2即为VRPTW求解结果,文献[21]在求解的9个算例中,能搜索到7个算例的最优值,算例C103和C104未能搜索到最优值,这两个算例的求解结果与最优值的误差分别为0.10%,0.51%;从9个算例的平均值来看,文献[19]所求得的路径成本均值为841,相较于最优解的平局值来说,误差到达了1.52%,文献[21]结果的误差相对较小,但也有0.63%,而本文的自适应大规模邻域搜索算法能搜索到全部算例的最优解.

表2 需求确定速度恒定条件下测试数据结果Table 2 The results of demand determine and constant speed

表3 需求确定的TDVRPTW求解结果Table 3 The results of TDVRPTW that requirement determination

由表3结果对比可知:不同的速度时间依赖函数下,在车辆使用数方面,本文算法求得的路径所需车辆数都为10辆,求解结果稳定;在路径成本方面,本文计算结果均优于文献[19]的计算结果;与文献[18]的计算相比较,本文仅在TD3a,TD3c 速度时间依赖函数下的求解结果稍差,在其它10种速度时间依赖函数下的求解结果均优于文献[18],ALNS较IECE、SA相比性能优势明显.综上说明本文算法性能较优,在求解客户需求确定的TDVRPTW问题时,能求到较好的解.

4.2 TDVRPFDTW算例求解验证

4.2.1 预优化方案求解

为验证ALNS算法对TDVRPFDTW依旧合理有效,选取并改进与TDVRPFDTW对应的TDVRPTW算例C101对模型及算法进行测试,时间依赖函数类型采用TD1a,在处理客户点需求模糊时保持原有客户点需求为d,其模糊需求为((1−γ)d,d,(1+γ)d),其中γ=0.25,偏好值α∈(0,1],求解时令α按幅度0.1递增.不同偏好值下,路网中客户需求模糊且车辆行驶速度时变的10次预优化结果如表4所示,表中N为最优值所需的车辆使用数,%Dev为最优值、最差值较均值的偏差.

由表4可见:最优值和最差值相对平局值的偏差较小,说明ALNS算法在求解TDVRPFDTW问题时性能稳定.另外,不同决策者偏好值α对预优化结果有较明显的影响,从表4中最优值可以看出,随着决策者偏好值α的增大,配送成本整体呈现变高的趋势,α在0.1∼0.5之间时,配送成本较低且比较稳定,最低成本为965,当0.9α0.6时,配送成本明显变高,α为0.9或1时,配送成本最高为1056.综上,在带时间窗约束且客户需求模糊的时间依赖型车辆路径问题中,决策者越趋向于冒险型,即对于一次性配送成功的渴望程度越高,其需付出的实际配送成本就相对越低;反之,决策者越趋向于保守型,对于一次性配送失败的承受程度越低,其需付出的实际配送成本相对越高.

表4 需求模糊且速度时变条件下的10次预优化结果Table 4 Results of the 10 pre-optimizations under the time-varying speed and fuzzy demand

从表4的结果可知,本文求得的最优预优化方案的预优化成本为965,完成配送任务需要12辆车,相应的预优化路径如图6所示.

4.2.2 重调度

由前文分析可知,在TDVRPFDTW问题中,即使通过计算对某一客户进行配送的可信性Crα,也无法保证对其配送任务一定可以完成,由此而产生的额外行驶距离就是决策者在选择偏好值的一个重要考虑因素.本文对表4所得预优化方案继续进行后续需求模拟求解,在预设的每个α值下最优预优化方案均单独求解10次,求解结果平均值如表5所示,表中Best是每个α下最优预优化方案的成本,其中ce表示由于客户点模糊需求模拟后路径中失败点存在所导致的额外成本,ct表示方案总成本,N表示最终方案中所需的车辆数.

图6 最优预优化路径图Fig.6 The chart of optimal pre-optimization routes

从表5中的结果可以看出,随着决策者偏好值α增大,由配送失败而产生的额外成本总体上呈下降趋势,说明了当决策者越趋向于保守型,配送时出现服务失败的可能性越小;当α为0.9或1时,配送的额外成本为0,即决策者保守程度极高时,不会出现服务失败点,此时的方案总成本也最小,最小总成本为1056;当决策者风险偏好极高时,即偏好值α为0.1时,路线所需的车辆数最多,所需车辆数比无服务失败点时所需的车辆数多15.38%,这说明在决策者风险偏好极高时,很容易产生服务失败点,从而需要新增派车辆完成后续配送任务.

表5 α递增下各最优预优化方案的调整结果Table 5 Adjustment results of each pre-optimization scheme under α increasing

为分析预优化方案与最终配送方案实际成本的关系,分别计算本文最优预优化方案重调度结果与α为0.9或1时的最优预优化方案重调度结果,其重调度结果对比如表6所示.其中全文最优预优化方案(以下简称方案1)的预优化成本为965,α为0.9或1时的最优预优化方案(以下简称方案2)的预优化成本为1056.

表6 不同预优化方案重调度结果Table 6 Results of re-dispatch on different pre-optimization schemes

从表6可知,方案1在实际配送过程中有路径4和路径9两条路径出现服务失败点,即需新增两辆车完成配送任务,完成所有配送任务实际需要14辆车配送,较预优化方案需要的12辆车增加了16.67%,且实际总成本为1127,相较于预优化方案的成本965增加了16.79%.方案2在实际配送过程中不会出现服务失败的情况,完成配送任务需要13辆车配送,总成本为1056,相较于方案1的实际配送成本1127低5.41%.在车辆使用数方面,方案2完成配送任务所需的车辆数为13辆.这较方案1实际所需车辆数少7.14%.综上,在本文的算例中,最优预优方案所需的实际成本不一定最低,其实际所需的车辆数也并非最少,当决策者偏好值α为0.9或1时,即决策者十分保守时,配送过程不会出现服务失败的情况,且完成服务所需的车辆和实际总成本相对较低.

5 结论

本文在对TDVRPFDTW问题的研究中,基于模糊可信性理论对客户点模糊需求进行处理,以Ichoua速度时间依赖函数来刻画动态路网,构建旅行速度时变且有时间窗要求的模糊机会约束优化模型;在预优化阶段,设计自适应的大规模邻域搜索算法对模型进行求解,在得到预优化路线后,采用随机模拟算法模拟客户的真实需求,对于服务失败点及其后续点,执行重调度策略进行调整;通过对改进的Solomon算例中C1类算例集的计算验证本文模型及算法的有效性,可得出以下结论:1)本文所建模型能够有效解决TDVRPFDTW问题,所设计的ALNS算法搜索性能良好、有效性高,是求解这类问题的有效方法;2)在TDVRPFDTW问题中,最优预优化方案所需的实际成本并不一定最低.在预优化阶段,随着决策者偏好值的增大,即决策者越趋向于保守型,其付出的配送成本反而越高,方案所需车辆数也有所增加;在重调度阶段,决策者越趋向保守,其付出的额外成本就相对越低,实际所需车辆数也相对较少.

本文的研究更符合实际配送场景,研究成果不仅进一步丰富和拓展了VRP相关理论研究,也可对物流企业配送优化决策提供科学依据.未来将在开发更加有效的求解算法及减少服务失败后的额外成本方面进一步展开研究.