事件触发下多智能体系统一致性的干扰主动控制

刘远山 杨洪勇 刘 凡 李玉玲 杨怡泽

(1.鲁东大学信息与电气工程学院,山东烟台 264025;2.新南威尔士大学电气工程与信息学院,悉尼)

1 引言

受到自然界中动物集体运动(或者集群、编队)行为的启发,人们发现由多个具有自主“计算”能力的个体组成的分布式网络系统通常能够完成相对复杂的任务,且具有单个个体所不具有的能力.多智能体系统的一致性控制[1–4]作为分布式多智能体协同控制的基础,在智能交通、无人机编队、分布式计算等领域的广泛应用引起了研究者的关注.

在实际的工程应用中,控制系统总能受到未建模动态,参数摄动和外部干扰等影响,这些不确定因素会严重影响着系统的动态性能.文献[5]通过研究垂直轴磁悬浮轴承中的旋转扰动,设计了一种非线性扰动观测器来估计干扰,最终使得系统达到稳定值.文献[6–8]通过干扰观测器可以有效估计外部扰动,设计了基于干扰观测器的控制协议,使得具有固定拓扑和变换拓扑的多智能体系统达到一致稳定.文献[9]研究了存在外部干扰的时滞高阶多智能体系统,并利用L2–L∞方法研究了系统的一致性问题,并且得到了闭环系统达到一致的条件.针对直流–直流(direct current-direct current,DC–DC)降压变换器的控制和鲁棒性分析问题,文献[10]提出了一种基于扰动观测器的控制方法.该方法通过构造干扰补偿增益,消除了输出电压通道中不匹配的不确定性扰动.文献[11]对现有的扰动或者不确定性估计方法进行了系统和全面的回顾,讨论了各种补偿技术和集成干扰等不确定性补偿.文献[12]研究了带有异质扰动的一阶多智能体系统的平均一致滤波问题,设计了干扰观测器估计系统中存在的扰动,利用矩阵理论和频域分析,在没有和具有相同通信延迟的情况下分别得到了系统收敛的充要条件.在上述的研究中,大都考虑的是连续时间系统的情形,智能体的状态信息不断地在各个节点之间传输,这就会占用大量的网络带宽,并且消耗大量的能源.为了解决上述问题,文献[13–15]中提出多智能体系统的事件触发控制机制,分别研究了集中式触发、分布式触发和自触发等控制策略.文献[16]研究了分布式一阶多智能体系统的领导跟随一致性,文中提出控制协议中的领导者的控制协议为全局信息.文献[17]研究并给出了非线性多智能体系统的基于Lyapunov方法和驻留时间方法两种事件触发机制的设计策略.文献[18]针对强连通网络提出一种自适应事件触发控制方案,该方案根据采样数据动态改变系统参数实现触发时刻间隔的动态调节.文献[19–20]中研究了异构多智能体系统的输出收敛问题,设计了一个事件触发下的输出控制机制.文献[21]研究了基于事件触发机制的高阶非线性多智能体系统领导者跟随一致性问题,控制协议采用基于相邻智能体的相对输出量的反馈控制方法,最终推导出系统一致收敛的充分条件.文献[22]针对一阶多智能体系统研究了其事件触发的一致性问题,文中采用了领导跟随结构的自适应一致性算法,智能体的控制输入由集中式事件触发条件决定.另外,考虑了多智能体系统在具有相同输入延迟的情况,并且获得了线性矩阵不等式形式的一致性收敛条件.

在实际应用中,多智能体的输入通道中不可避免地会存在外部扰动.干扰的存在会影响到系统的运动状态,所以研究干扰对系统产生的影响是十分必要的,但现在对于这个问题的研究相对较少.本文在总结前人研究工作的基础上设计了一种线性干扰观测器估计系统中出现的扰动,并提出了一种基于事件触发机制的干扰主动控制协议,研究了具有干扰的多智能体系统一致收敛的充分条件.

符号说明:表示向量或矩阵的欧几里德范数;符号AT表示矩阵或向量A的转置;使用1N(0N)来表示所有元素为1或者0的N维列向量,符号diag{x1,x2,…,xn}表示对角元素xi为对角矩阵;用符号A ⊗B表示矩阵A和B的Kronecker积.

2 预备知识与问题描述

智能体与外部系统之间的信息交流一般是通过无向图或者有向图来描述.一个图可以被描述为G=(V,ε),其中:V={1,2,…,N}是一个与N个智能体相关联的非空点集,ε ⊆V ×V是该智能体集合的边集.(i,j)∈ε意味着节点i可以从节点j获取信息,节点j叫做节点i的邻居节点,节点i的邻居的集合可以定义为Ni={j:(i,j)∈ε}.加权邻接矩阵被定义为如果(i,j)∈ε,那么aij=aji>0,否则aij=0.在这里,本文假设aii=0,i∈IN,这就意味着每一个节点没有自环.与邻接矩阵A相关联的拉普拉斯矩阵定义为lij=−aij,

在本文中,考虑有N个跟随者智能体和一个领导者智能体组成的多智能体系统的领导跟随一致性问题.跟随者智能体与外部的领导者智能体之间的通信拓扑图用是一个节点集,并且是一个边集;节点0代表领导者(外部系统).定义bi为跟随者和领导者之间的连接权重,其中i=1,2,…,N.令B=diag{b1,b2,…,bN},如果第i个跟随者与领导者连通,则bi >0,否则bi=0.

为了方便下面的公式推导与证明,提出以下引理:

引理1[21]L为图G的Laplacian矩阵,

1)λ1=0是L中的一个特征值,且其对应的特征向量为1,即满足L1=0;

引理2[23]对于任意维度的矩阵M,N,P和Q,并且M和N是可逆矩阵,Kronecker积具有以下特性:

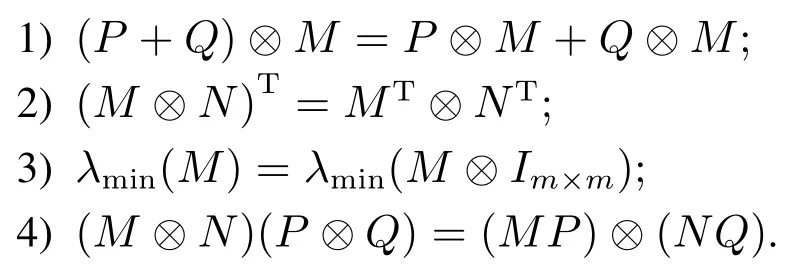
考虑一个带有领导者的多智能体系统,其中跟随者i的动力学方程为

假设1假设干扰di(t)在控制通道中为谐波噪音或者周期性的噪声,它可以用如下外部系统来表示:

定义1(领导跟随一致性)如果对于任意的初始状态x0(0)和xi(0),存在控制输入ui(t)可以使得

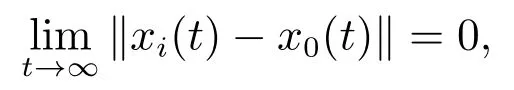
对于所有的智能体i均成立,则多智能体系统(1)达到了领导跟随一致性,其中i=1,2,…,N.

3 事件触发机制下多智能体系统的干扰主动控制

3.1 分布式干扰观测器的设计

引理3假设多智能体系统(1)的状态是可以获得的,构造系统(1)的干扰观测器如下:

证定义干扰观测器的干扰误差

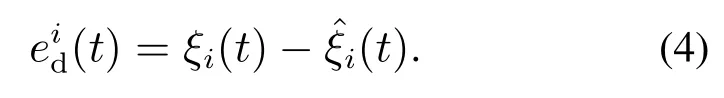
由干扰观测器(3)和干扰估计误差(4)得到

由于(W,Y)是可观测的,则一定存在矩阵K,使得矩阵(W −KY)是Hurwitz的,那么误差系统(5)是渐近稳定的.因此干扰观测器的干扰估计误差(t)能够渐近地跟踪系统(1)中的干扰实际值. 证毕.

3.2 分布式事件触发机制

针对带有外部扰动的领导跟随多智能体系统(1),其传统的连续时间下的一致性控制协议为

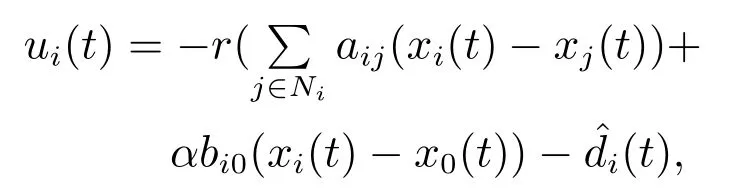
其中:r >0,α>0为待设计的控制协议的反馈控制增益,为干扰估计项.

为了降低跟随者智能体控制协议的更新次数,节约智能体有限的计算资源和能源的消耗,所以针对智能体i设计分布式事件触发函数∇i(t).由∇i(t)0得到一系列离散的事件触发时刻

其中:k=1,2,…代表第k次的事件触发时刻,i=1,…,N.设计第i个智能体的分布式事件触发下的领导跟随一致性控制协议为

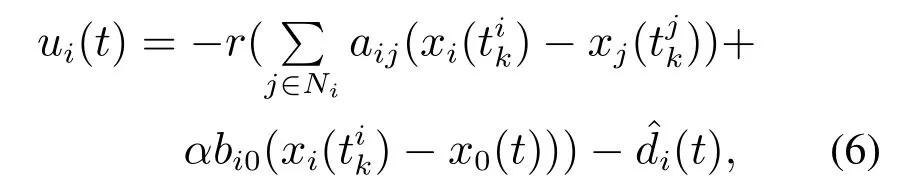
注1一致性控制协议(6)中所用到的采样状态量为在事件不被触发的时间段内,两个采样值均存放在临时的寄存器或者零阶保持器中,当第i个(或者第j个)智能体的事件分别被触发的时候才会更新相应的(或者

3.3 带有匹配干扰的多智能体系统一致性分析

为了分析多智能体系统(1)在控制协议(6)的作用下能够实现领导跟随一致性.定义状态误差ei(t)=那么

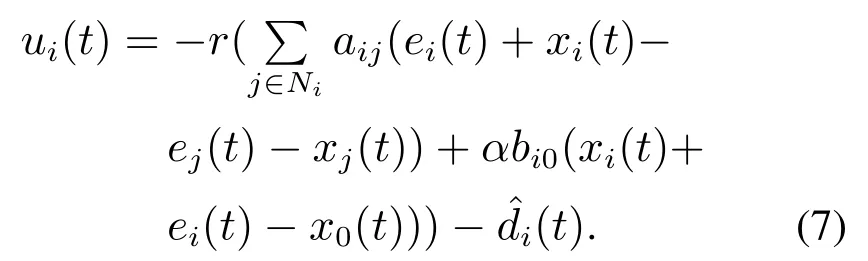
那么多智能体系统(1)变更为

定理1如果多智能体系统(1)的拓扑结构是固定拓扑,且具有一棵全局生成树,领导者为根节点.对于任意的xi(t)|t=t0∈m选取合适的0<ηi <1,∀i∈{1,2,…,N},设计分布式事件触发函数如下:

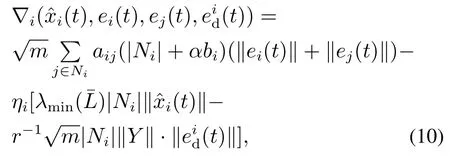
其中:r >0,α>0为控制协议的控制增益,|Ni|表示了智能体i的直接相连的邻居智能体的数目.在控制协议(6)的作用下,当时,多智能体系统(1)可以实现领导跟随一致性.

证构造Lyapunov函数

对于状态误差ei(t),可以得到

所以

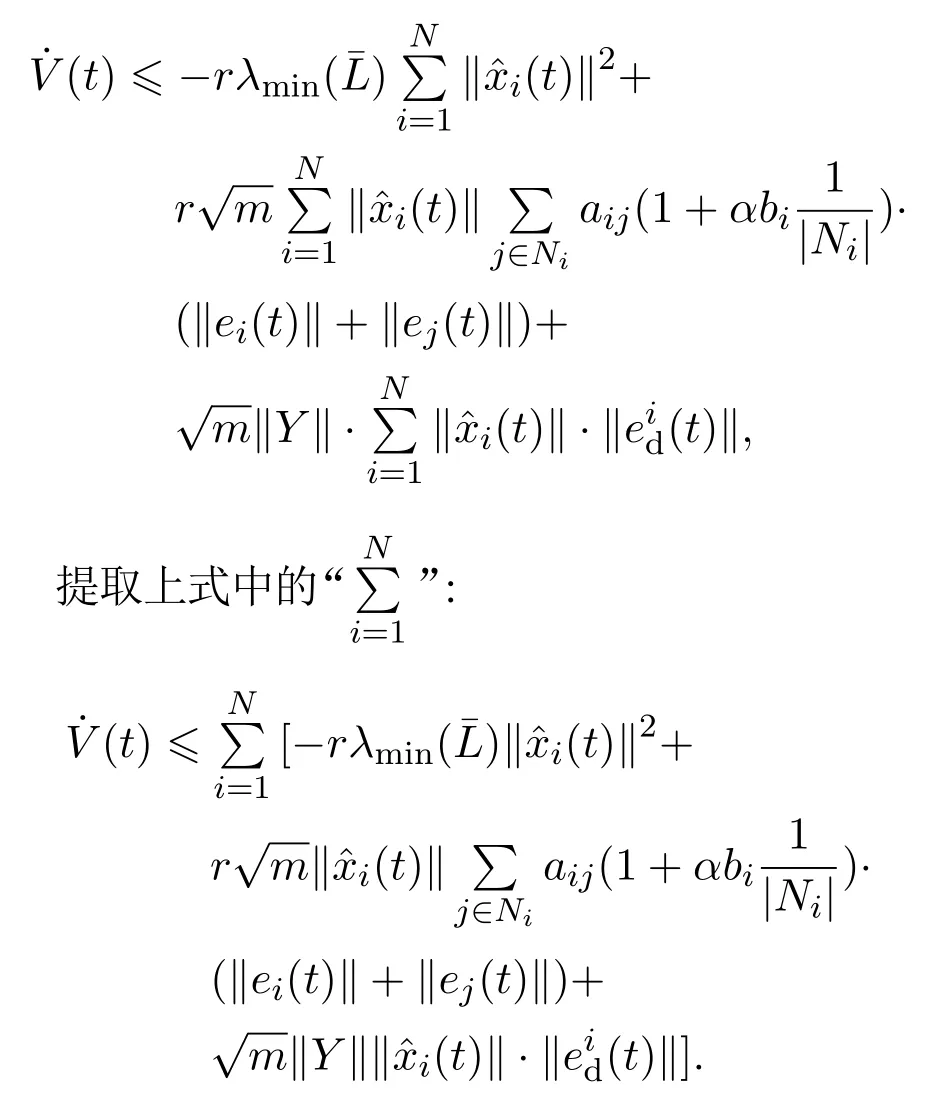
如果存在ηi∈(0,1]可以使得

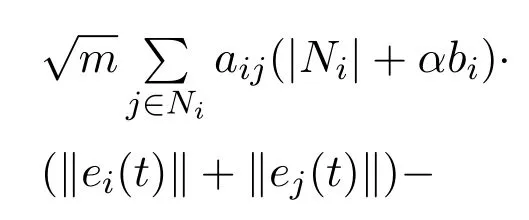
注2由于该事件触发条件是分布式的,对于智能体i只要满足事件触发控制器将会提取自身及其邻居的状态来更新控制器(6).

注3在分布式事件触发函数(10)中的为方程(5)的解.因为在引理1中被证明是渐近稳定的,所以是有界的.由于事件触发函数(10)中实际干扰与估计的干扰值的误差项是存在的,所以使得变得更容易满足,并且该项使得(10)变为更加保守的触发条件.

当两个事件触发时刻之间的间隔为0时,称为芝诺效应.如果出现这种情况,则事件触发机制不能被使用.为表明本文所提事件触发策略不会在极小的时间段内被触发无限次,特给出如下定理及其证明.

定理2假设图中Leader作为一个全局可达点,考虑带有一个领导者的多智能体系统(1)–(2),应用一致性协议(6)和分布式事件触发函数(10).则多智能体系统(1)–(2)中的任意一个智能体q,得到的所有的触发时刻为τ0… τk τk+1,它的任意两个连续事件触发时刻之间的间隔不小于

证构造(t)/(t)的动力学方程如下:

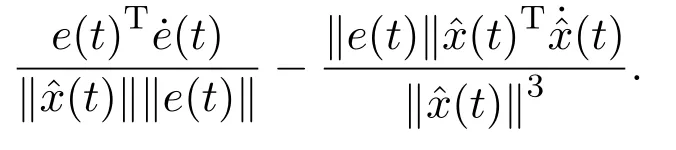
当t∈[tk,tk+1)时,

由于上式中ed(t)为观测器的估计值与输入通道中的外部扰动,通过上面的分析,可以得到所以可以将上式变为

解上式微分方程可得

所以,可以得到

证毕.

4 计算机仿真与分析

在这一部分,将利用MATLAB软件来仿真验证本文所提的控制算法和分布式事件触发函数.在本次实验中考虑由4个Follower和1个Leader组成的多智能体网络系统.假设每个Follower智能体的邻居为N1={4},N2={3,4},N3={2},N4={1,2},那么可以得到多智能体系统(1)如图1所示的拓扑结构.

图1 多智能体系统的通信拓扑图Fig.1 Communication topology of multi-agent systems

那么多智能体系统(1)相应的Laplacian矩阵和领导跟随矩阵如下:

假设外源干扰信号由以下外部系统产生:

应用线性矩阵不等式为了使矩阵(W −KY)为Hurwitz的,那么可以选取干扰观测增益K为[3 3]T.假设

分别为扰动系统(13)的初始状态.对于控制协议ui(t),选取

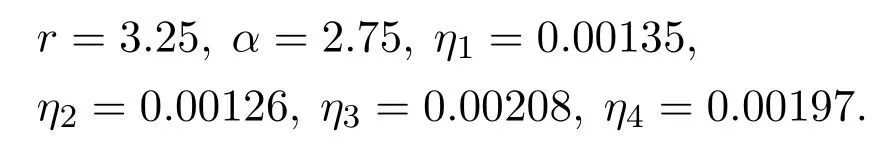
智能体的初始状态为

在上述初始状态下,按照给出的控制器来调控系统可以得到智能体位置状态仿真图2–3.

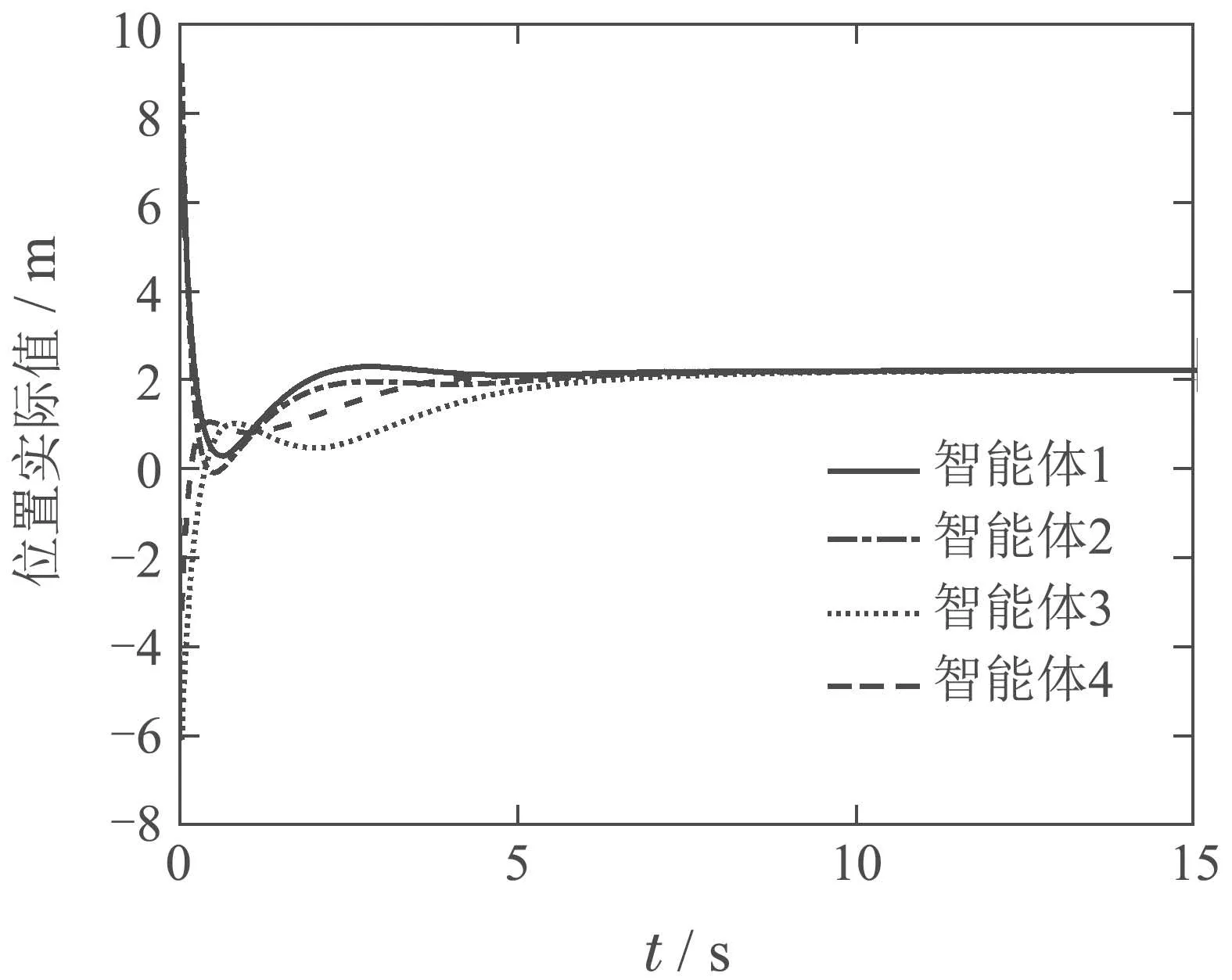
图2 带有外部扰动和干扰观测器的多智能体系统的运动轨迹Fig.2 Trajectories of multi-agent systems with external disturbance observer

图3 4个智能体干扰观测器的观测误差Fig.3 Observation errors of 4 agents with the disturbance observer

系统仿真图2是带有外部扰动和干扰观测器的多智能体系统的运动状态的实际值,尽管多智能体的输入通道中存在外部扰动的影响,但是由于控制协议中加入了扰动抑制项,4个跟随者的位置状态仍然可以一致起来并且跟踪到领导者,表现出了较好的控制效果.由此可以看出采用本文的控制协议和分布式事件出发机制能够抑制外部扰动的影响.

系统仿真图3是干扰观测器对受扰动多智能体系统(1)中每个智能体的干扰观测误差.干扰观测器能够计算出智能体的输入通道中存在的扰动,各个智能体的观测误差很快趋近于0.说明干扰观测器可以估计出时变的干扰,从而表现出良好的性能.

表1为带有外部扰动的多智能体系统在分布式事件触发机制下的事件触发次数和触发比率,由表中数据可以看出采用本文的控制协议可以大范围降低智能体的采样和控制器的更新次数.

表1 4个跟随者智能体的事件触发次数和触发比率(存在扰动带有扰动抑制项)Table 1 Event-triggered times and ratios for 4 followers with disturbance rejection

由系统仿真图4可以看出每个智能体的事件触发时刻不是在同一时刻,表明本文设计的触发机制确实是分布式的.选取智能体4观察其误差范数,从系统仿真图5中可以看出,在多智能体系统刚开始运行的时候触发间隔较小且误差范数相对较大,随着时间的推移误差范数在不断减小且触发时刻变得稀疏,这与预期的结果是一致的.

图4 4个跟随者智能体的分布式触发时刻Fig.4 Distributed triggered intervals for 4 followers

图5 智能体4的状态误差的范数Fig.5 Error norms of 4 agents

为了更好地表明本文提出的基于事件触发的多智能体系统的干扰主动控制器的优势,在初始条件和控制参数相同的情况下与文献[16]的结果进行比较.系统仿真图6是基于事件触发的控制算法但是没有对扰动进行抑制的智能体系统的运动状态,从图6中以看出如果不对通道中的外部干扰进行适当的抑制,那么多智能体系统的位置状态将不能达到渐进一致,且无法追踪到系统中领导者.系统仿真图7表示每个智能体的事件触发时刻,与系统仿真图4相比较事件触发时刻更加密集且不均匀的.

通过比较表1和表2可以发现,当存在外部扰动时,变化幅度较大的状态会使得事件触发机制变得更容易触发,从而增加了事件触发的次数和频率,本文基于分布式事件触发和干扰主动控制的领导跟随一致性算法不仅可以消除扰动的影响,更能减少事件触发次数和节约多智能体系统的通信资源.

图6 具有外部扰动但不带干扰观测器的多智能体系统的运动轨迹Fig.6 Trajectories of multi-agent systems without external disturbance observer

图7 4个跟随者智能体的分布式触发时刻Fig.7 Distributed triggered intervals of 4 followers

表2 4个跟随者智能体的事件触发次数和触发比率(无扰动抑制项)Table 2 Event-triggered times and ratios for 4 followers without disturbance rejection

5 结论

本文考虑了带有外部扰动的多智能体系统在固定无向拓扑结构下的领导跟随一致性问题,提出了一种基于干扰观测器的分布式事件触发控制机制.控制器的状态更新依赖于触发函数,本文在分布式事件触发机制的控制下每个智能体可以实现领导跟随一致.通过理论分析证明了本文所设计的分布式事件触发机制不会存在芝诺行为.仿真结果表明本文所提事件触发控制算法能够抑制扰动,并且能实现多智能体系统的领导跟随一致性.

实际的多智能体系统的拓扑结构往往不是固定不变的,所以,下一步的工作将是对在切换拓扑和有向图的情况下的多智能体系统事件触发领导跟随一致性的研究.