一种高精度Σ-ΔA/D转换器的数字滤波器设计

郭书宏 刘云涛 杨璐

（哈尔滨工程大学信息与通信工程学院 黑龙江省哈尔滨市 150001）

Sigma-delta(Σ-Δ)ADC是一种基于噪声整形和过采样技术的高精度模数转换器，与逐次渐进型、flash型、双积分型等ADC相比，更容易达到更高的精度[1]。数字滤波器作为Σ-Δ ADC的重要组成部分，主要负责对调制器输出的高频信号进行解码和降采样处理，并滤除带外噪声，实现高精度数字信号的重构。

为实现高效低资源滤波，本文设计的数字滤波器采用多级多采样率结构，由级联梳妆滤波器（CIC）、FIR补偿滤波器以及半带滤波器（HF）级联组成。同时采用乘法器时分复用技术和CSD编码技术，降低面积和功耗，使设计具有精度高、功耗低的特点。

本文基于MATLAB分析仿真进行设计，并进行硬件实现仿真。

1 数字滤波器的结构设计

数字滤波器是Σ-ΔADC中面积最大，最复杂的器件，其主要功能是对调制器输出的低精度数字信号进行处理，输出高精度低速率的数字信号[2]。本次设计基于MATLAB进行设计，设计的数字滤波器系统框图如图1所示。

第一级使用CIC滤波器，其结构简单，不需要进行乘法运算，高降采样率的特点可以大幅降低后续电路复杂度[3]；第二级使用FIR滤波器对CIC滤波器的通带滚降进行补偿，同时进行二倍抽取；第三级使用半带滤波器滤除带外噪声并将输出频率降至奈奎斯特输出频率。各级滤波器的输入输出采样频率和降采样率如表1所示：

图1：滤波器系统框图

图2：CIC幅频特性

图3：1-CIC滤波器；2-Cascade滤波器；3-补偿滤波器

1.1 CIC滤波器

CIC滤波器是FIR滤波器中最优的一种,由一对或多对积分-梳妆滤波器级联组成。结构简单，没有乘法器，只有加法器、加法器和寄存器，适合于工作在高采样率条件下。而且CIC是一种基于零点相消的FIR滤波器[4]，因此在高速抽取系统中是非常有效的单元。多级级联CIC的系统函数如下：

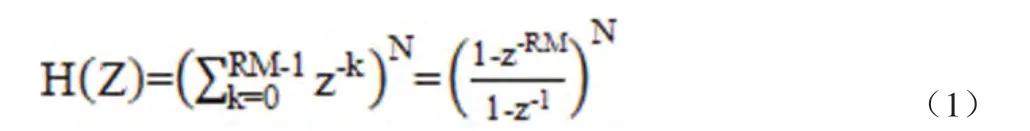
式中，N为CIC滤波器级数，R为抽取率，M为梳妆单元的差分延迟。其频率响应为：

设计CIC时，若降采样率较大，会缩小主瓣宽度，增加带内衰减，增大第2级补偿滤波器的阶数；若降采样率较小，会增加后续滤波器个数，增加硬件开销。综合考虑，本次设计采用32倍抽取，4级级联结构，差分因子为1。

通过MATLAB仿真得到CIC滤波器。幅频特性如图2所示。

1.2 FIR补偿滤波器

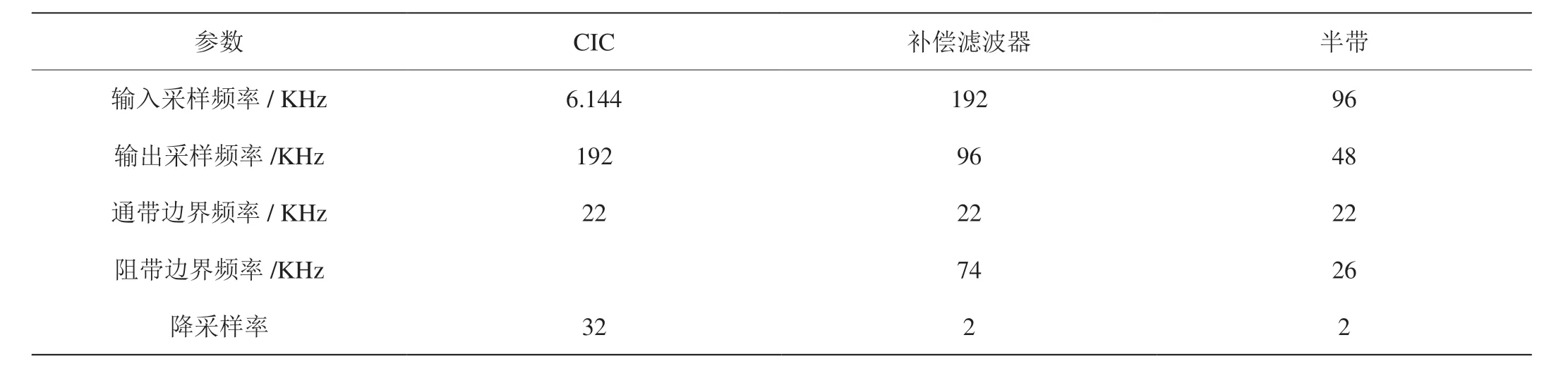
表1：各级滤波器指标

表2：几种滤波器的主要性能对比

从CIC滤波器的幅频特性可以看到，在通带边缘有0.8dB的衰减，设计要求通带衰减在0.01dB之内。因此需要对CIC滤波器进行带内补偿。由于补偿滤波器的过渡带较宽，因此阶数可以设计的较低，同时需要实现二倍抽取。补偿滤波器本质是一种FIR滤波器[5]，可以实现线性相位。设计的补偿滤波器通带纹波为0.0075dB，阻带衰减110dB，幅频特性如图3所示。

可以看到，20KHz通带内衰减小于0.01dB，达到了补偿的目的。

1.3 半带滤波器

半带滤波器是一种非常适合于2倍抽取滤波器，它除了最中间的系数为0.5，其他奇数项系数都为0而且系数具有对称性。此外它的通带截止频率和阻带截止频率关于1/4采样频率对称，即通带容限和阻带容限相等。因此，经半带滤波器滤波后，进行二倍抽取时，信号通带内没有频谱混叠[6]。而且设计半带滤波器时只需要给出过渡带宽度即可知道通带截至频率和阻带开始频率。本次设计的半带滤波器阻带衰减为110dB。幅频特性如图4所示。

1.4 三级级联数字滤波器

将设计的CIC滤波器、FIR补偿滤波器和半带滤波器级联，在simulink中进行仿真。输入调制器输出6.144MHz的数字信号，经128倍抽取滤波后后输出，分析输出信号的幅频特性，如图5所示。

1.5 乘法器的时分复用

除CIC滤波器外，FIR补偿滤波器和半带滤波器都需要使用多个乘法器。通常电路的做法是先将对称项相加，再与系数相乘，这样当滤波器阶数较高时，会需要大量乘法器。本设计采用乘法器时分复用技术，只需要一个乘法器，大幅减小芯片面积。结构如图6所示。

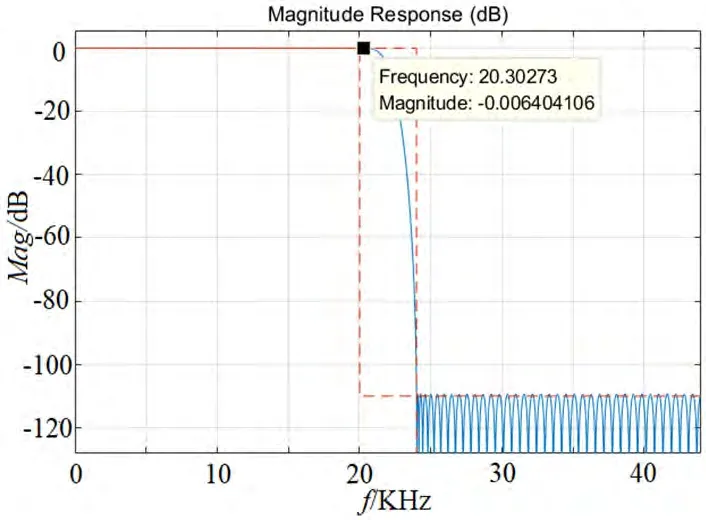
图4：半带滤波器幅频特性

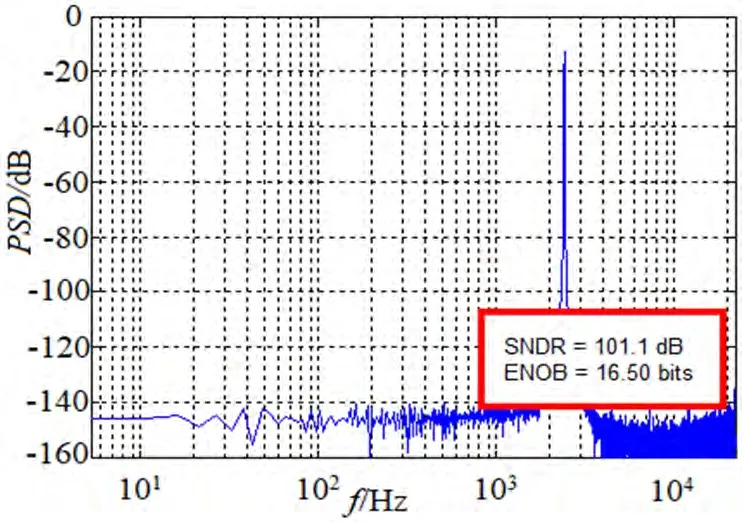
图5：仿真输出信号幅频特性

图6：乘法器时分复用结构

图7：Verilog仿真

图8：输出信号幅频特性

输入数据在采用时钟CLK1的控制下输入到MUX1中，然后在计算周期CLK2的控制下，通过MUX2的选择与指定系数进行相乘，并通过累加器与上一计算周期结果相加。当所有计算完成后将计算结果通过寄存器进行同步输出。

2 Verilog仿真验证

MATLAB设计时使用的是理想系数，进行Verilog实现时需要进行有限位系数处理。此外，为减小芯片面积，采用正则有符号数（CSD）编码来实现。对于一个二进制浮点数来说，CSD编码两个相邻位只能有一个为1。从低位到高位,如果发现"11"(两个连续的"1")，就用10(-1)表示。因为11=100-001，后面以此类推。如下：

图9：数字滤波器版图

对系数CSD编码后可以有效降低乘法器的个数，节省硬件资源。对编写的RTL级Verilog代码进行仿真验证，结果如图7所示。

调制器输出信号经过CIC滤波器32倍降采样后输出正弦信号data_out_cic,再经过FIR补偿滤波器补偿和进一步降采样后输出为comb_filter_out,最后通过半带滤波器进一步降采样后输出为halfband_out。将输出导入到MATLAB中进行傅里叶变换，分析其幅频特性，计算的sndr=100.1dB，ENOB=16.34bit。如图8所示。

完成对数字滤波器的仿真验证之后，采用simc 0.18CMOS工艺对其进行综合、布局布线、后仿真等操作，最后完成的版图如图9所示。

表2列出几种抽取滤波器的性能参数，可以看出，在相同或更低过采样率的同时，本文提出的抽取滤波器可以实现更高的设计精度。和文献[7]相比，在相同的带宽和过采样率下，信噪比提高10dB，有效位数提高两位。

3 结论

本文基于MATLAB设计了一种可适用于高精度Σ-ΔADC的数字抽取滤波器，该滤波器由级联梳妆滤波器（CIC）、FIR补偿滤波器以及半带滤波器级联组成。并使用乘法器时分复用和CSD编码技术，降低系统的面积和功耗。最终可以实现在20KHz的带宽下对6.144MHz的调制信号进行128倍降采样和滤波。并完成了数字滤波器的系统建模仿真，对设计的滤波器进行Verilog硬件实现仿真和版图设计，最终可以达到100dB以上精度，使设计具有高精度、低功耗的特点。