基于模态挠度的斜交桥静载试验数值方法

亓兴军，赵 越，赵 奇

(1. 山东建筑大学 交通工程学院，山东 济南 250101； 2. 山东建筑大学 山东省高校土木结构防灾减灾协同创新中心，山东 济南 250101)

0 引 言

桥梁是供铁路、公路、渠道、管线等跨越河、山谷或其他障碍的具有承载能力的架空建筑物，是交通设施互联互通的枢纽点和关键点[1]。随着中国交通运输行业的不断发展，公路运输量日益增长，超速、超重车辆也不断增加，给公路桥梁带来巨大的压力，再加上复杂的环境因素影响，严重影响了桥梁的使用性能和结构安全，使得桥梁的承载能力和使用寿命迅速降低。因此，对于桥梁运营状态进行有效快速的评估具有重要的意义。

评估桥梁状态的方法有经验评定法、综合评定法、荷载试验法和影响线法[1-6]。目前主要应用荷载试验法对桥梁运营状态进行安全性评估。荷载试验按照加载方式不同可分为静载试验和动载试验。静载试验的主要方法是选用等效于设计荷载的车辆荷载对桥梁进行加载，测量桥梁的静载应变和静载挠度，可以对桥梁承载力进行较为直观的评估。经过多年的发展，桥梁静载试验已形成了完整的理论和方法，相关部门已颁布了相应的规范与标准，广泛应用于现役大中型桥梁承载力状态评估。由于静载试验流程复杂，加载时间长，且需要中断交通，耗费大量的人力物力，所以难以广泛应用于小型桥梁承载力状态评估[7-8]。然而桥梁模态挠度的测量较为简单，且不需要中断交通在桥面加载试验车辆，只需要在桥面布置加速度传感器，利用环境激励或者交通激励，获得桥梁的动力响应数据，再对响应数据进行模态分析，获得桥梁各阶的模态参数，进而计算出桥梁的位移柔度矩阵[9-10]。利用位移柔度矩阵可以计算桥梁在静载试验工况下各控制面模态挠度，代替静载试验的实测挠度，从而评价桥梁承载力状态。基于模态挠度评估桥梁承载力的方法具有成本低、时间短、操作方便等优点，能弥补传统静载试验中必须长时间中断交通的缺点，具有广阔的工程应用前景。

本文以龙山桥为研究对象，建立空间梁格有限元模型，探讨基于模态挠度的静载试验评估斜交桥梁承载力的可行性。

1 模态位移柔度计算方法

1.1 模态位移柔度定义

柔度表示的是结构在单位力作用下的位移，与刚度互为倒数，可以表征结构在线弹性状态下的变形能力，对结构的损伤定位、定量和性能评估具有明确意义[11]。按照测试方法不同可以将柔度分为静力位移柔度和模态位移柔度，通过静力试验和静力分析方法得到的柔度称为静力位移柔度；通过模态试验及模态分析方法得到的柔度称为模态位移柔度[12]。理论上，如果能有足够多阶的模态阶数用于计算结构的柔度，那么就可以得到精确的柔度数值。在忽略测量误差的前提下，假设结构处于线弹性状态下，其模态位移柔度与静力位移柔度在数值上是相同的[2]。利用位移柔度矩阵可以预测桥梁在已知荷载作用下的模态位移，从而代替静力位移。如今，常用2种方法计算模态位移柔度：方法1，基于角频率和附加质量的质量归一化振型计算模态位移柔度；方法2，基于频率响应函数拟合提取模态位移柔度[11]。本文采用附加质量方法计算结构的模态柔度矩阵。

1.2 振型质量归一化计算方法

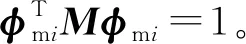
(1)

φmi=γiφi

(2)

1.3 模态位移柔度计算方法

由结构振动理论可知，位移频响函数H(ωi)在力学概念中等同于单位动荷载作用下各测量点的动位移[13]。在实际工程中，桥梁的结构阻尼较小，可设为比例阻尼。根据一般阻尼的复模态理论，取所有测点为参考点时，可以得到基于实模态理论位移频率响应函数H(ωi)的模态分解公式[13]，即

(3)

式中：ω为外部激励角频率；ξi为第i阶模态的阻尼比。

观察公式(3)可知，H(ωi)为外部激励角频率ω的函数矩阵。当ω→0时，H(ωi)表示单位荷载作用下结构某一点的位移，物理意义表示的是结构的柔度矩阵Hd[12]，即

(4)

Hd的物理意义是结构的柔度矩阵，因此Hd可由结构的模态信息推导出来，称之为结构的模态柔度矩阵。由结构的模态柔度矩阵Hd和静荷载向量f，可计算得结构的竖向挠度D

D=Hd·f

(5)

由公式(5)可以看出，柔度矩阵的计算公式是各阶模态参数的叠加形式，与原结构固有角频率的平方成反比，随着模态阶次的升高，结构的固有角频率显著增大，高阶模态参数对位移柔度矩阵的贡献将显著减小。因此，一般结构只需要前几阶模态参数计算位移柔度矩阵，其预测的模态位移会快速收敛于结构的真实静力位移，就能满足工程精度要求[14-15]。

2 工程实例

2.1 龙山桥工程概况

龙山桥位于道路直线段内，与龙山村西河道交角为70°，宽度为11.61 m，桥梁全长56.04 m。桥梁设计采用3～13.0 m简支梁桥，上部结构采用装配式先张法预应力混凝土简支空心板，共12块。下部结构为桩柱式桥墩和重力式桥台扩大基础。桥梁现场照片如图1所示。

2.2 龙山桥有限元模型

本桥为斜交板桥且桥面横向宽度较大，桥梁在荷载作用下变形值的横向分布采用单梁模型无法准确模拟，因此本文用梁格模型进行模拟，梁格模型采用MIDAS/Civil软件建模[16]。主梁、横隔板以及虚拟横梁均采用梁单元，其中假设虚拟横隔梁的刚度为无限大，纵梁基于腹板划分，虚拟横梁刚度根据剪力梁格理论计算。全桥模型共577个节点、962个单元。斜交板桥的简支边界条件根据支座约束方向采用相应的一般支承来模拟。

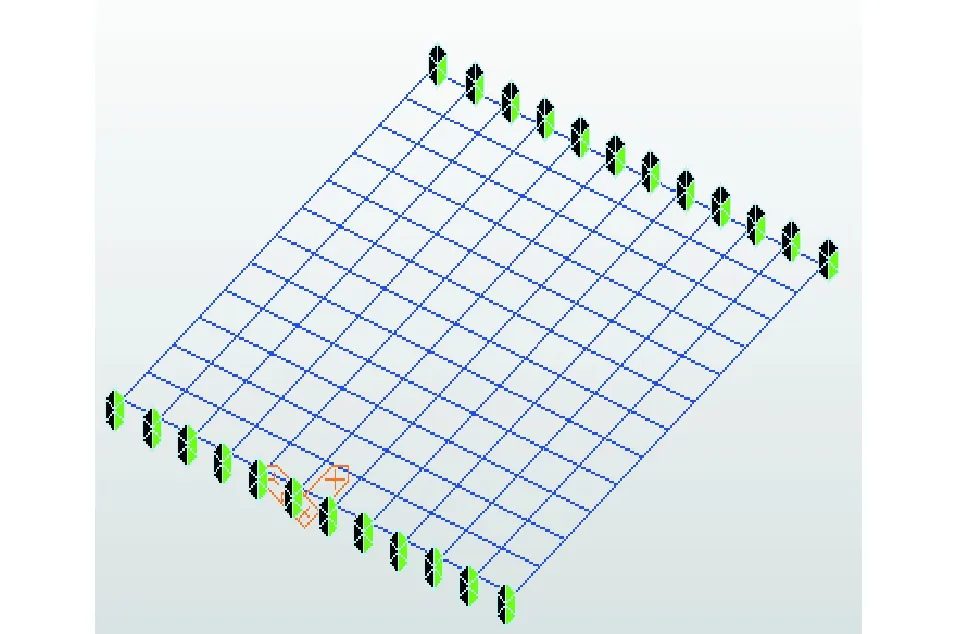
为了直观模拟实际环境激励下的桥梁随机动力响应，桥梁有限元模型的所有节点施加时长为60 s、零均值的高斯白噪声激励，利用有限元模型计算桥梁结构在振型节点作用有高斯白噪声的加速度响应[15]。选取每单片简支板梁的13个有限元节点作为振型测点，在空心板底面共模拟布置156个加速度传感器。桥梁有限元计算模型如图2所示，高斯白噪声时域如图3所示。

3 位移柔度矩阵计算

3.1 桥梁结构模态参数

基于桥梁模态参数识别的模态挠度法应用于桥梁承载力评估时，由于位移柔度矩阵的快速收敛性，只需要利用低阶竖向振型对应的模态参数便可以计算得到较为精确的位移柔度矩阵[11]。在实际工程应用中，只需要在桥面布置竖向加速度传感器，测量桥梁在环境激励下的竖向加速度，运用模态分析法得到桥梁结构前几阶竖向振型对应的模态参数。在桥梁有限元结构中施加高斯白噪声激励，模拟真实的环境激励；空间斜交板桥结构较为复杂，有限元计算得到的振型包括竖向、横向和扭转等形式。本文的目的是使用竖向振型计算位移柔度矩阵，根据各阶模态振型质量参与百分比可知：前5阶振型均为竖向，且第5阶振型累计竖向振型质量参与系数为77.26%；从第6阶开始，桥梁结构振型表现为横向和扭转。同时考虑到位移柔度矩阵的快速收敛性，故选用前5阶竖向振型计算位移柔度矩阵。桥梁未附加质量时的前5阶竖向频率和振型如表1所示。

表1龙山桥环境激励模态频率和振型Tab.1Ambient Excitation Modal Frequency and Mode Shape of Longshan Bridge

表2附加质量时龙山桥环境激励模态频率和振型Tab.2Ambient Excitation Modal Frequency and Mode Shape of Longshan Bridge with Additional Mass

3.2 龙山桥位移柔度矩阵

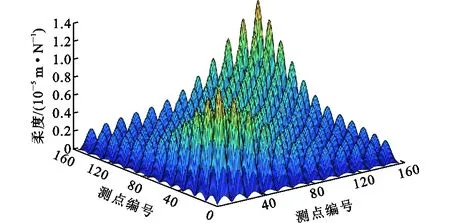
将环境激励下龙山桥有限元模型的基本模态参数代入公式(1)和公式(2)，计算桥梁结构的质量归一化系数γ和质量归一化振型φmi，前5阶振型质量归一化系数γ分别为1.02，1.06，1.02，1.09，1.08。可以看出，每一阶振型的质量归一化系数都不一样，其数值的大小与振型的幅值以及附加质量的大小和位置都有关系。再利用公式(4)计算柔度矩阵为156行156列的方阵，为直观地观测该矩阵，画出如图5所示的三维矩阵图，由于156个传感器测点在横桥向大概沿着12根梁布置，所以位移柔度矩阵的三维曲面有144个明显的峰值，最大峰值点对应桥梁结构的位置为边梁跨中处。峰值点较为密集说明静力荷载作用于桥梁单元时，本单元节点的荷载会对其他单元的模态挠度有影响，这个结果与该梁格结构的物理意义是一致的。

4 桥梁模态挠度计算

为了验证基于模态挠度法静力荷载试验的方法所计算挠度的准确性，将利用柔度矩阵所计算的模态挠度数值与有限元结果的理论值进行比较。按照《公路桥梁承载能力检测评定规程》(JTG/T J21—2011)中关于桥梁静载试验加载方案的要求，采用3辆30 t的三轴车对龙山桥进行加载，加载车辆示意如图6所示。根据规程要求，利用桥梁的影响线及试验荷载效率，确定加载试验中最不利活荷载位置，设计中载和偏载2种工况进行加载试验。中载工况车辆加载位置如图7所示；偏载工况车辆加载位置如图8所示。在桥梁有限元模型中，车辆荷载按照集中荷载形式进行加载，集中荷载的形式如图6所示。通过有限元软件分别计算得到龙山桥2种工况下在的静载挠度理论值。

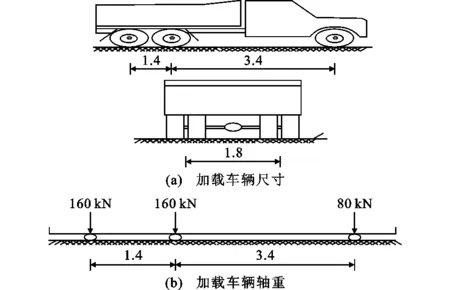
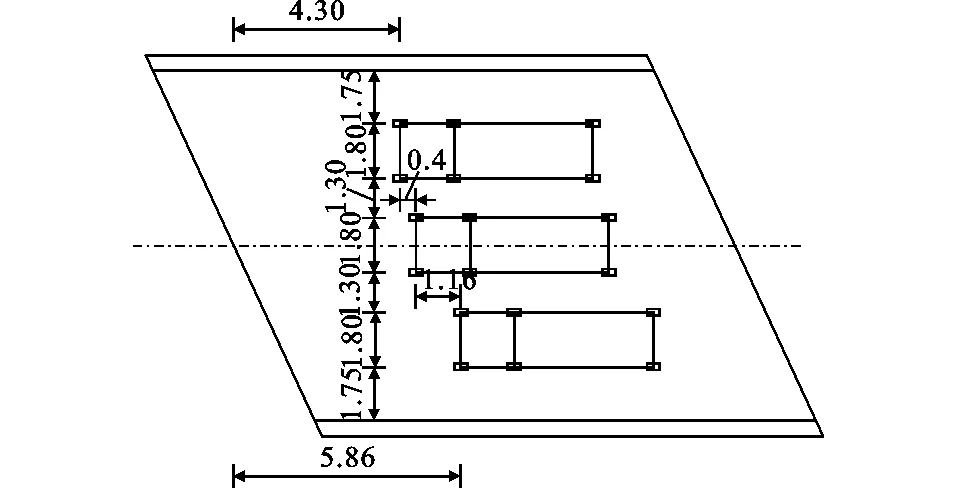
在计算模态挠度时，需要对车辆荷载进行节点等效荷载分配，按照等效荷载的原则将车轮力分配到柔度矩阵的计算节点上，然后利用节点等效荷载与柔度矩阵计算桥梁的模态挠度[17-19]。

4.1 中载工况挠度计算

中载工况为3辆加载车辆，进行了实际中载下的挠度测量，结果如表3所示。利用有限元与位移柔度矩阵计算各控制截面的模态挠度，结果如表4所示，各测点的挠度曲线如图9所示。

由表3中数据可知：在中载工况下，各测点挠度校验系数位于0.26～0.42之间，满足规程要求；相对残余位移介于0%～14.81%之间，满足评定规程和试验规程中不大于20%的规定，说明中载工况设计合理。选取每根梁挠度最大的截面为控制截面，模态挠度值与实测值相比，各控制截面变化规律相同。利用环境激励下的前5阶模态参数计算得到的桥梁模态挠度数值与有限元分析的理论挠度值相比，各节点相对误差均小于5%，其中边梁的控制截面模态挠度计算的相对误差最大，最大相对误差为3.55%，满足工程精度要求。

4.2 偏载工况挠度计算

偏载工况下，每根梁挠度最大点的数值和相对误差如表5所示，各测点挠度的曲线如图10所示。

表3中载挠度实测结果Tab.3Measured Results of Deflection Under Medium Load

表4中载挠度最大值相对误差Tab.4Relative Error for Maximum Deflection Under Medium Load

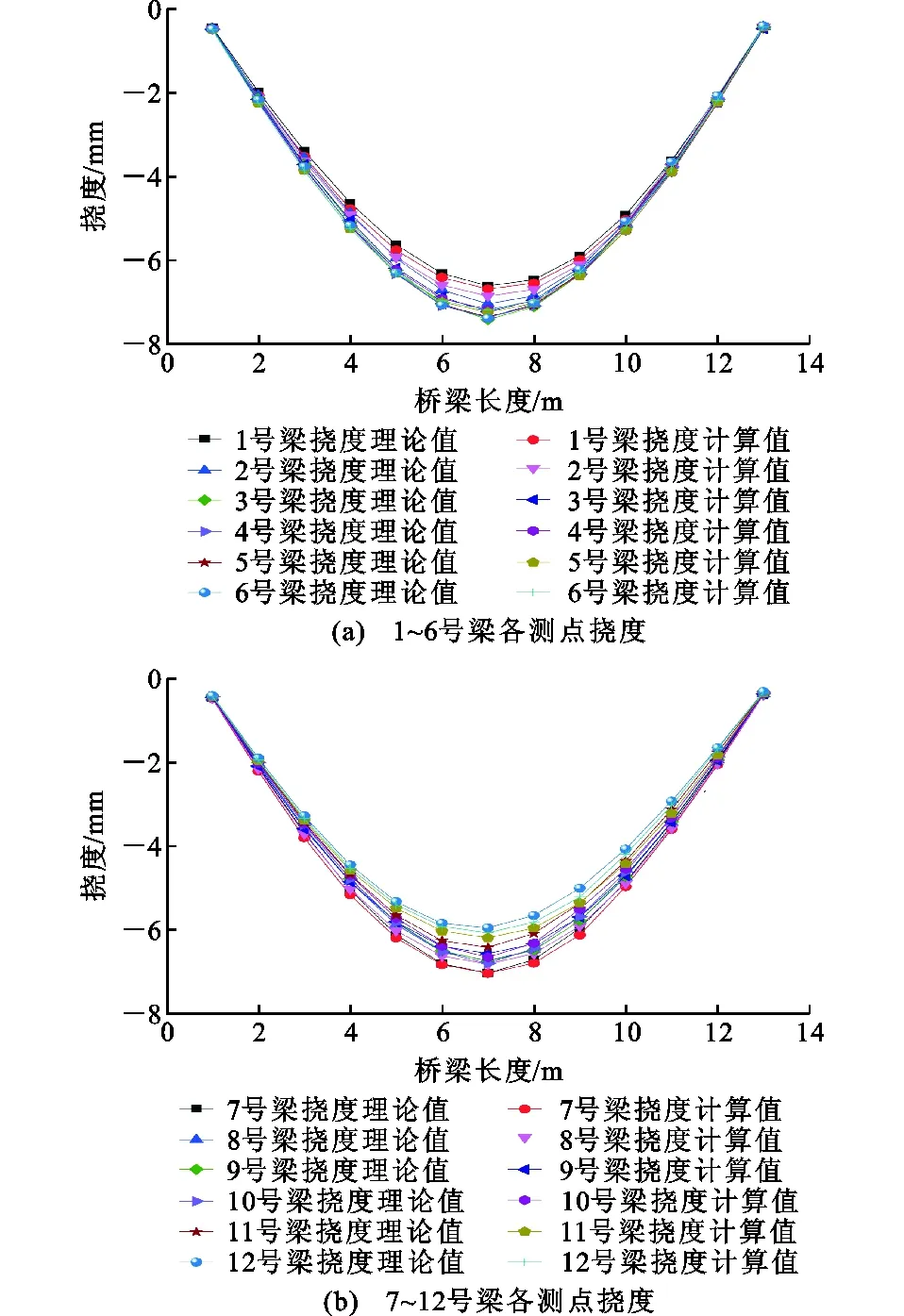
对于龙山桥而言，在偏载工况下，利用环境激励下的前5阶模态参数计算得到的桥梁模态挠度数值与有限元分析的理论值相比，各控制截面相对误差均在8%以内，控制截面最大相对误差为7.58%，基本上可以满足工程精度要求。

5 结 语

(1)利用模态挠度法，通过结构的前5阶模态参数计算桥梁结构在静载试验荷载作用下的模态挠度，与静载理论挠度相比较，中载相对误差均小于6%，偏载相对误差小于8%，满足工程精度的要求，说明模态挠度法能够有效替代静载试验挠度，可以应用于桥梁的承载力评估。

表5偏载挠度最大值相对误差Tab.5Relative Error for Maximum Deflection Under Partial Load

(2)在中载和偏载2种工况下，中载工况计算的误差小，偏载工况计算的误差大。说明在通过柔度矩阵预测桥梁的模态挠度时，中载工况的加载位置更接近于计算柔度矩阵的峰值点，计算结果更准确。

(3)通过柔度矩阵计算的桥梁模态挠度和有限元计算结果相比，仍然存在误差。原因在于计算柔度矩阵时加速度采集的测点数目不足，导致柔度矩阵计算的维数不够；或者是节点荷载分配不够精确，计算桥梁模态挠度时会存在误差。

(4)基于模态挠度的静载试验法结合了模态分析与静载试验的优点，在实际工程中，可以在不中断交通的情况下，只需利用环境激励或者是交通激励，便可以方便快捷地测量得到相关的结构模态参数。因此基于模态挠度的静载试验方法具有广泛的应用前景。