圆端形钢管混凝土中长柱轴压性能

任志刚，张 铭，魏 巍，王丹丹

(武汉理工大学 土木工程与建筑学院，湖北 武汉 430070)

0 引 言

钢管混凝土具有承载力高、塑性韧性强等优点，性能优良且便于施工，被广泛应用于工程实际中，国内外对圆形、矩形钢管混凝土的研究已经较成熟。圆端形钢管混凝土是一种圆弧形与矩形结合的新型截面形式，抗弯能力强，横向刚度大，稳定性强且具有优良的约束性能，已被广泛应用于桥梁工程中，如武汉市后湖斜拉桥主塔等工程。

文献[1]对圆端形钢管混凝土构件受扭性能进行分析，提出了核心混凝土本构关系等效计算方法，并得出圆端形钢管混凝土受扭极限承载力简化公式;文献[2]～[4]采用有限元软件对圆端形钢管混凝土轴压短柱受力机理进行分析，结果表明圆端形钢管混凝土约束性能、承载力、峰值应变和延性均介于圆形和矩形之间；文献[5]对圆端形钢管混凝土短柱进行轴压试验，提出了圆端形钢管混凝土轴压短柱承载力公式；文献[6]，[7]对采用不同构造措施的圆端形钢管混凝土构件进行轴压试验并分析不同构造措施对构件性能的影响，提出了带纵向隔板的圆端形钢管混凝土轴压短柱极限承载力计算公式；文献[8]～[10]对圆端形钢管混凝土构件进行偏压研究，分析偏心率对承载力的影响并进行参数分析；文献[11]，[12]对耐候钢管和微膨胀混凝土构件进行试验和有限元分析，比较与普通圆端形钢管混凝土构件的性能差异。目前国内外对圆端形钢管混凝土研究主要集中在短柱，缺少对中长柱的试验研究及理论分析。在工程实际中，多使用大长细比钢管混凝土构件，其破坏形态及受力性能与短柱不同，短柱的规范公式不适用于中长柱，因此有必要对圆端形钢管混凝土中长柱性能进行研究，以完善圆端形钢管混凝土体系，并为工程实际应用提供理论依据。本文利用ABAQUS有限元软件建立圆端形钢管混凝土模型，分析中长柱和长柱轴压力学性能，并分析主要参数对构件性能的影响，提出了圆端形钢管混凝土中长柱轴压极限承载力计算公式。

1 试件设计

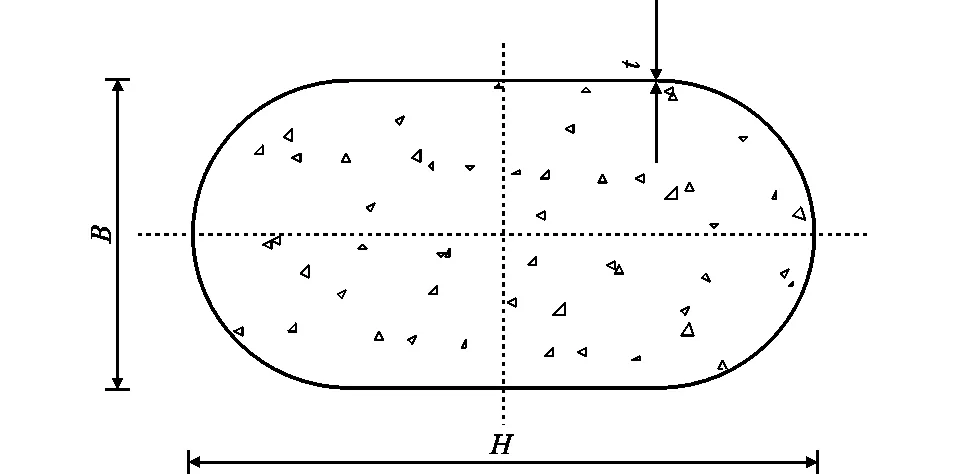
图1为圆端形试件截面示意图，其中，H，B分别为截面的高度与宽度，t为钢管的厚度。为研究长细比、钢材性能、含钢率、混凝土强度、高宽比对圆端形钢管混凝土中长柱性能的影响，设计了21个试件，试件的长细比范围为10.8～96.0，其中RCFST-a1为短柱对照试件，基本参数见表1。

2 有限元模型

2.1 材料的本构关系模型

混凝土单轴受压应力-应变关系及相应的参数取值参照文献[13]中方形、矩形钢管核心混凝土本构模型，根据约束效应相等的原则，将圆端形截面视为高、宽分别为H，B,转角半径为B/2的带转角矩形截面[8,14]，具体关系如下

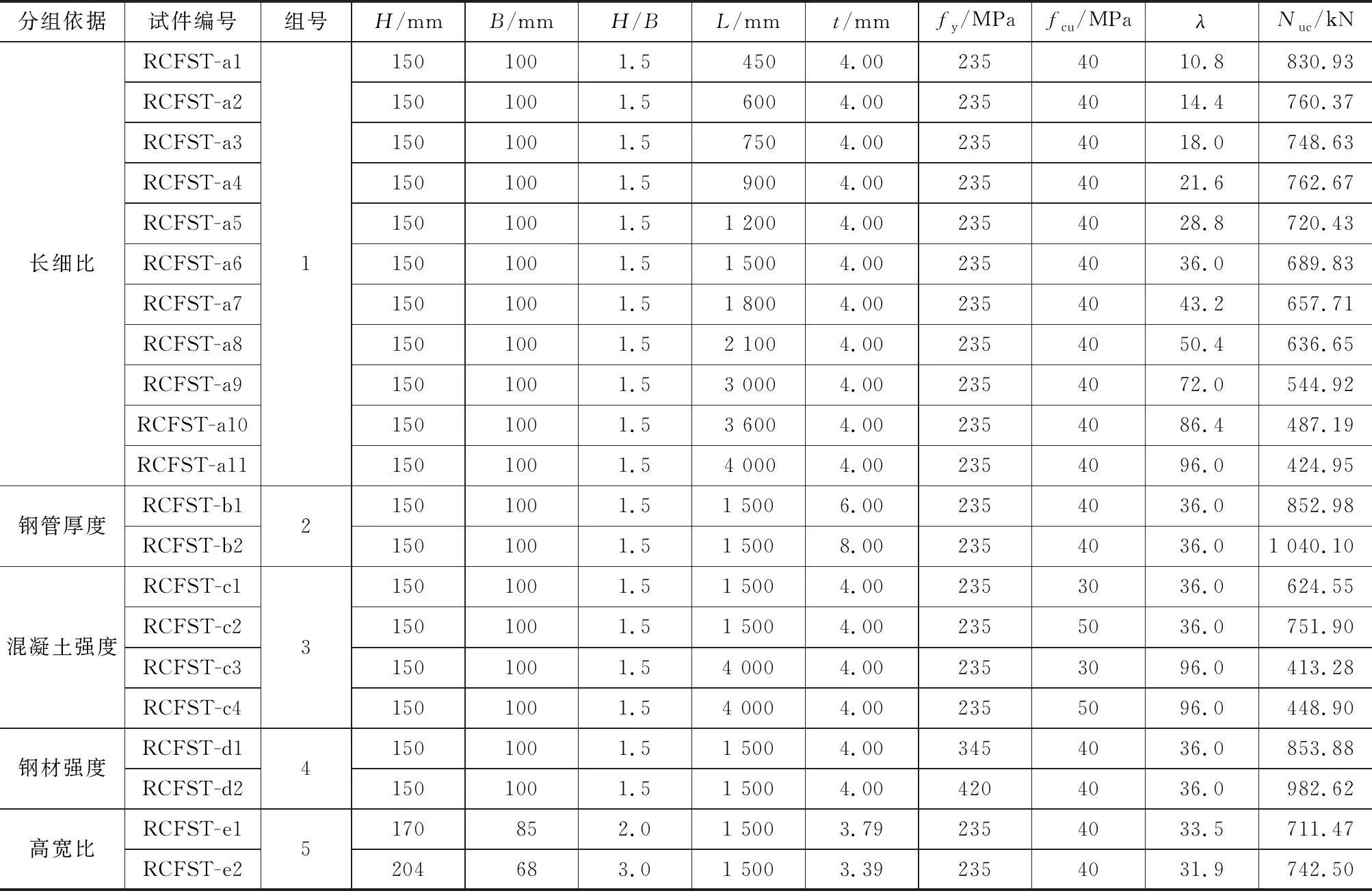
表1试件基本参数和极限承载力Tab.1Basic Parameters and Ultimate Bearing Capacities of Specimens

注：L为构件设计长度；fy为钢材屈服强度；fcu为混凝土轴心抗压强度设计值；λ为构件长细比；Nuc为构件极限承载力。

(1)

ε0=εc+800ξ0.2×10-6

η=1.6+1.5/x

混凝土单轴受拉应力-应变关系按无约束混凝土考虑，采用图2所示的混凝土受拉软化模型，图2中σf和Ul分别为混凝土的应力和裂缝宽度，Ul0对应的应力为0，Gf为断裂能，C20混凝土的Gf取为40 N·m-1，C40混凝土的Gf取为120 N·m-1，中间插值计算。混凝土开裂应力σt0按照式(2)进行计算[15]，即

(2)

钢管的应力-应变关系[16]为

(3)

式中：σi为钢管的等效应力；εi为钢管的等效应变；εy为钢管的屈服应变；εyt为钢管的强化应变，取εyt=12εy；εu为钢管达极限强度时的应变，取εu=120εy；ζ为系数，取ζ=1/216；fu为钢材极限强度，取fu=1.5fy；取钢管弹性模量Ey=2.06×105MPa。

2.2 有限元模型的建立

采用ABAQUS进行建模，圆端形钢管混凝土的外包钢管选用4节点的壳单元，核心混凝土及加载板采用8节点三维实体单元，加载板为刚性面。模型网格划分采用结构化网格划分技术，如图3所示。加载板与核心混凝土采取绑定约束(tie)形式；钢管与加载板采用壳与实体耦合；钢管与混凝土采用摩擦型接触，切线方向的接触选取库仑摩擦定义，摩擦因数定为0.5[5],法线方向定义为“硬接触”，允许钢管与混凝土之间有微小的有限滑移。

柱子采用位移加载的方式，上端截面约束沿X，Y方向的位移，施加沿轴向(Z轴)的竖向位移荷载；下端截面约束沿X，Y，Z三个方向的位移。为了模拟试验中刀口铰的边界条件，放松柱子端部屈曲轴方向的转角位移，约束其他2个方向的转角位移。中长柱的初始缺陷对构件的力学性能有显著影响，取L/1 000的初始偏心距综合考虑[17]。

2.3 试验验证

3 ABAQUS结果分析

3.1 破坏模式

图5～7给出了典型试件各部分的应力云图。图5为典型短柱试件RCFST-a1在不同加载阶段时的钢管Mises应力和混凝土纵向应力云图，取承载力P上升至30%Pmax，85%Pmax，Pmax以及下降至75%Pmax四个受力阶段，其中Pmax为极限承载力；图8(a)为RCFST-a1的荷载-位移曲线。由图8(a)可知：在加载初期试件应力呈均匀分布，各处应力均很小，应力、应变为线性关系；随着荷载的增加，发生应力重分布，当荷载增大到85%Pmax时，钢管开始屈服，试件中部应力明显增大，出现鼓曲。达到最大承载力时，柱子高度降低。随后混凝土出现裂缝而逐渐退出工作，试件承载力下降，至85%Pmax时趋于平缓，说明短柱有较好的稳定性和延性。

图6为典型中长柱试件RCFST-a6各部分应力云图，图8(b)为RCFST-a6的荷载-位移曲线。由图8(b)可知，加载初期初始缺陷对中长柱的影响较小，柱子受力情况同短柱试件RCFST-a1，荷载达到85%Pmax时，试件发生偏心受力，开始产生侧移，钢管受力增大至极限强度后开始屈服，试件应力-应变曲线出现非线性变化，试件刚度减小，发生弹塑性失稳。

表2 试验数据与有限元计算数据对比Tab.2Comparison of Test Data and Finite Element Calculation Data

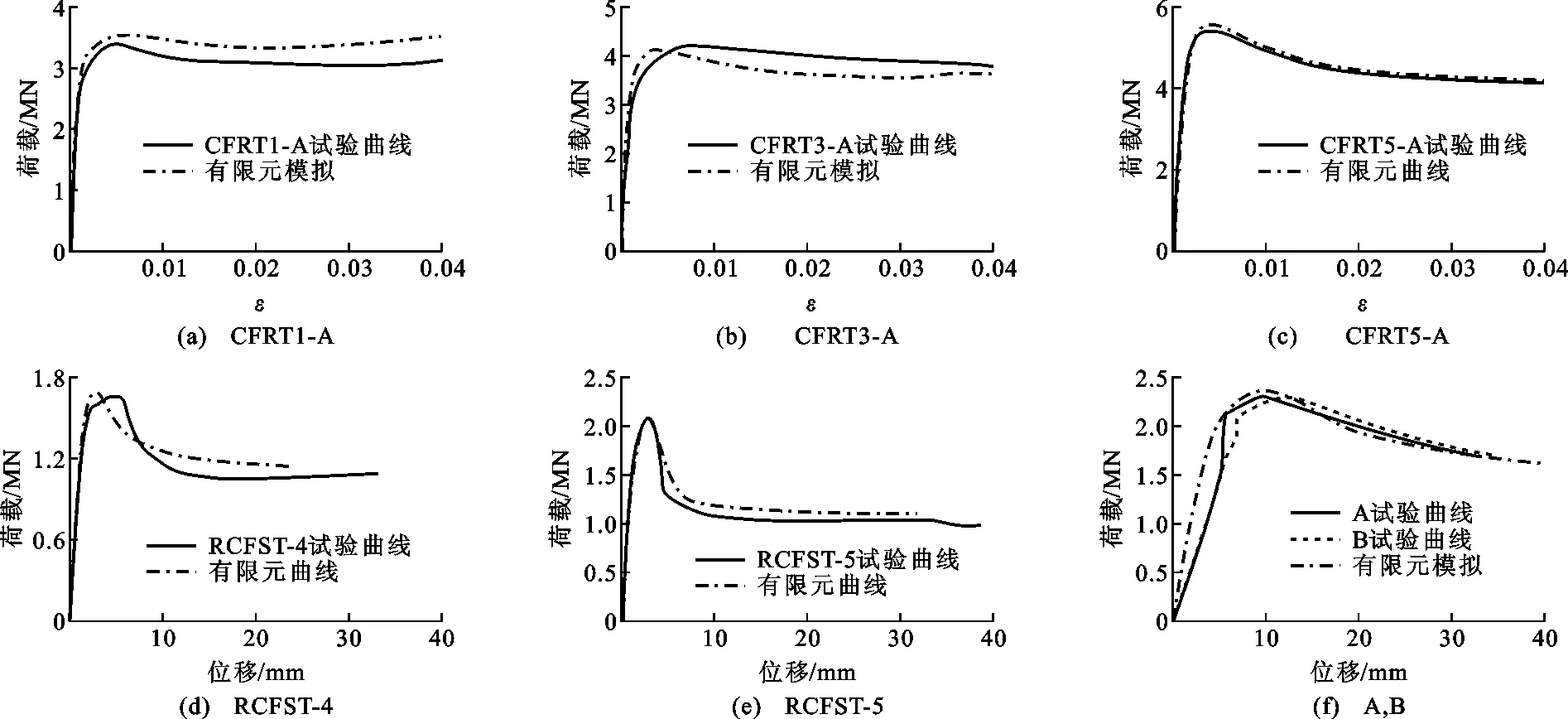
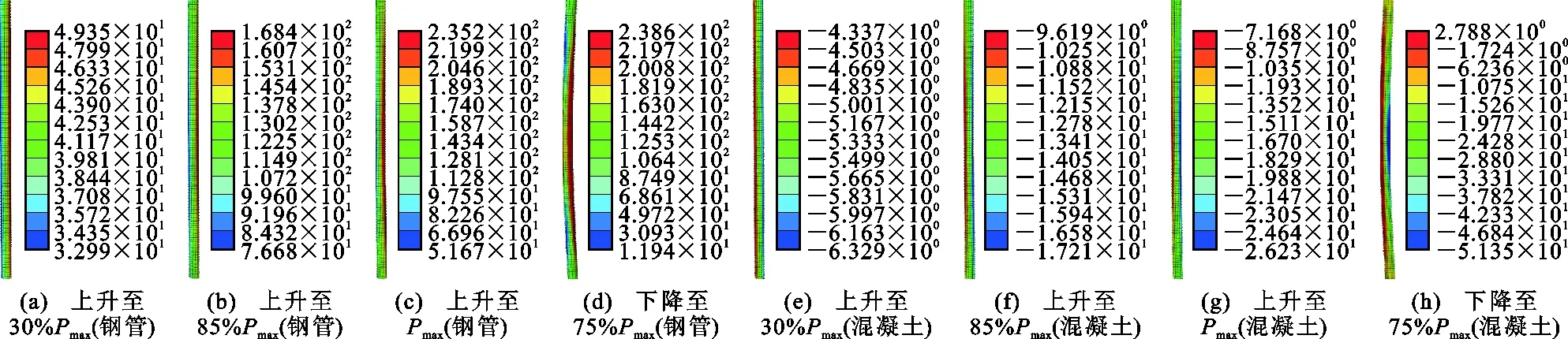
图7为典型长柱试件RCFST-a11各部分应力云图; 图8(c)为RCFST-a11的荷载-位移曲线。由图8(c)可知，在初始缺陷的作用下加载初期钢管已产生侧向位移，试件达到极限承载力时混凝土无明显裂缝，长柱中混凝土只起到支撑钢管的作用，试件承载力低，稳定性差。

3.2 荷载与钢管应变的关系

图9，10为试件荷载-钢管应变(P-ε)曲线，其中，正应变表示受拉，负应变表示受压。

长细比λ=36.0的试件轴压荷载下混凝土微裂缝扩大，塑性变形发展，环向应变明显增长；达到峰值荷载时全截面受压，随着位移荷载的增大，部分截面由受压转为受拉后退出工作，试件承载力下降，为典型中长柱的弹塑性破坏模式，见图9。

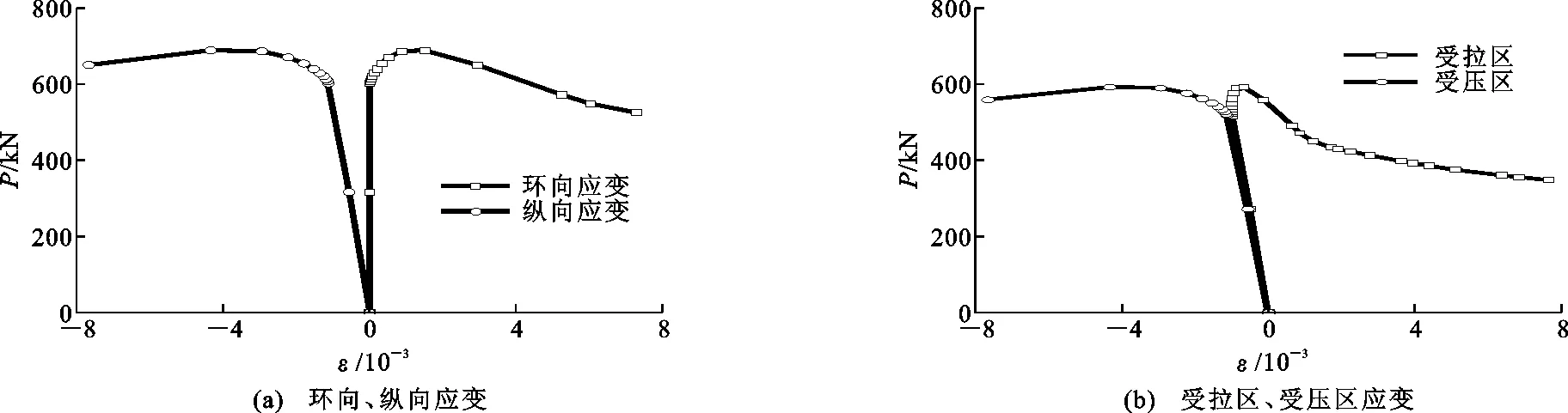
长细比λ=96.0的试件初始缺陷使试件发生屈曲，受力状态与压弯试件相似，在弹性阶段，轴压荷载下混凝土的初始弹性基本不变，环向应变增长较小，峰值荷载时受拉区截面由受压转为受拉。继续加载试件发生整体屈曲，为典型长柱试件的弹性破坏模式，见图10。

对不同长细比试件的P-ε关系曲线进行分析，判断试件的破坏模式，结果见表3。由图3可知，中长柱与长柱界限长细比λp=86.4～96.0。

4 参数分析

图11为不同参数变化下的试件荷载-位移曲线对比。由图11可知：随着长细比增大，试件极限承载力、初始刚度、延性均降低；混凝土强度变化对试件极限承载力、初始刚度、延性影响均较小；钢材强度提高，试件极限承载力增大，延性增加，初始刚度变化不大;钢管厚度增大，试件极限承载力和初始刚度有所提高，延性增强;高宽比增大，圆端形钢管混凝土试件极限承载力有所提高，初始刚度影响不大。

5 承载力极限公式

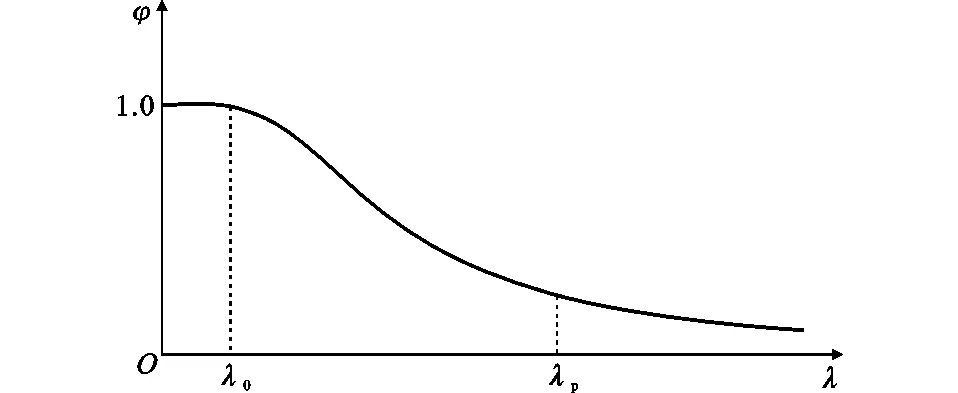
图12为钢管混凝土的稳定系数-长细比(φ-λ)关系曲线[13]其中，λ0为短柱和中长柱的界限长细比。λ0可按式(4)确定

(4)

(5)

式中：As为钢材截面面积；Ac为混凝土截面面积；α

⑤最大坝高、集水面积、库容信息完整的溃坝水库165例统计分布见图1，可见溃坝案例基本集中于库容100万m3以下、集水面积50km2、坝高30 m以下的小 （2）型水库，为138例，占165座水库的83.6%。说明小（2）型水库安全状况差，应为重点管理对象。

表3不同长细比试件的破坏模式Tab.3Failure Modes of Components with Different Slenderness Ratios

注：INB代表弹塑性破坏模式；EB代表弹性屈曲破坏模式。

为圆钢管截面含钢率；fck为混凝土轴心抗压强度标准值。

圆端形钢管混凝土中长柱轴压极限承载力Nu,cr为

Nu,cr=φNu=φAscfscy

(6)

Nu=Acfck[1+(0.8+0.9B/H)ξ]

(7)

式中：Nu为圆端形钢管混凝土短柱轴压极限承载力，其计算公式取自参考文献[5]；Asc为钢管混凝土柱截面面积；fscy为钢管混凝土柱轴压强度。

现将文献[5]和文献[6]中圆端形轴压短柱试验结果与公式(7)计算结果进行对比，见表4。结果表明，公式(7)可以准确计算圆端形钢管混凝土短柱极限承载力。

钢材屈服强度是影响稳定系数的主要因素[19-21]。表5为不同钢材标号下试件的承载力，表6为试件的稳定系数φ，φ=1时取界限长细比λ0。

由表6可知，当λ=10～11时，对应的φ值近似为1，取λ0=10～11。对比可知，该结果与方形钢管混凝土界限长细比公式计算结果较接近，故方钢管混凝土界限长细比公式适用于圆端形钢管混凝土。

稳定系数φ与长细比λ的关系式[13]为

(8)

(9)

b=e-2aλp

(10)

(11)

(12)

(1)对于圆钢管混凝土

(13)

(2)对于方形、矩形钢管混凝土

(14)

通过对96个有限元模拟结果进行回归分析，修正公式(13)，(14)得圆端形钢管混凝土系数d计算公式为

(15)

式(15)的判定系数R2=0.950 73。

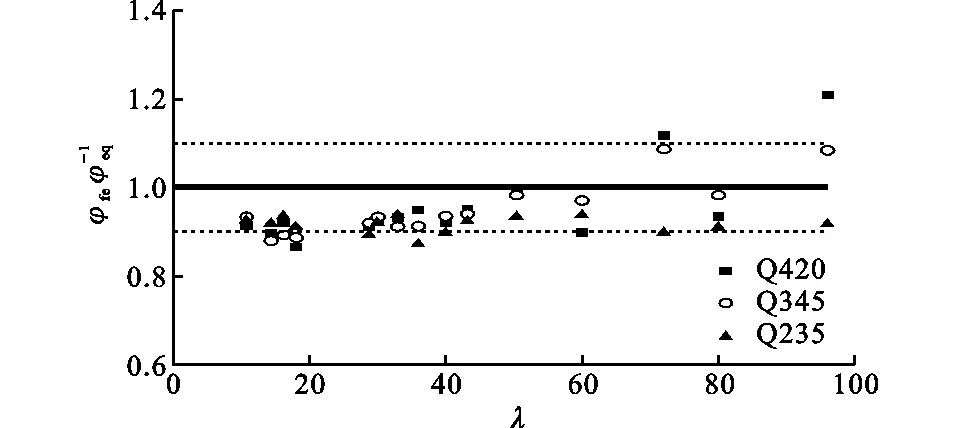
图13为表1各试件有限元计算稳定系数与按公式(8)计算稳定系数的比值与长细比的关系图，其中φfe为稳定系数有限元结果，φeq为稳定系数公式计算值。由图13可以看出，除个别试件较离散，2种方法计算所得稳定系数相差不大，相对误差控制在±10%之内。

选取文献[6]和文献[18]中6个圆端形钢管混凝土试件，长细比在10～18之间。将公式(6)～(15)计算所得极限承载力与试验结果进行对比，结果见表7。由表7可见，Nue/Nuc的均值为1.04，公式相对误差控制在±10%之内。因此，圆端形钢管混凝土中长柱轴压极限承载力简化公式计算结果较为精确。

表4极限承载力公式计算结果与试验结果对比Tab.4Comparison Between Formula Calculation Results and Test Results of Ultimate Bearing Capacity

注：Nue为极限承载力公式计算结果；Nuc为极限承载力试验结果。

表5不同钢材标号下试件承载力Tab.5Bearing Capacity of Different Steel Grades

表6稳定系数φ值Tab.6Stable Coefficient φ

6 结 语

(1)长细比是影响圆端形钢管混凝土形态的最主要因素。短柱发生屈曲破坏；中长柱发生弹塑性失稳破坏，未达到极限承载力时环向应变已有较大发展，达到极限承载力时全截面受压；长柱发生弹性失稳破坏，达到极限承载力时环向应变开始发展，受拉区截面由受压转为受拉，部分截面退出工作。

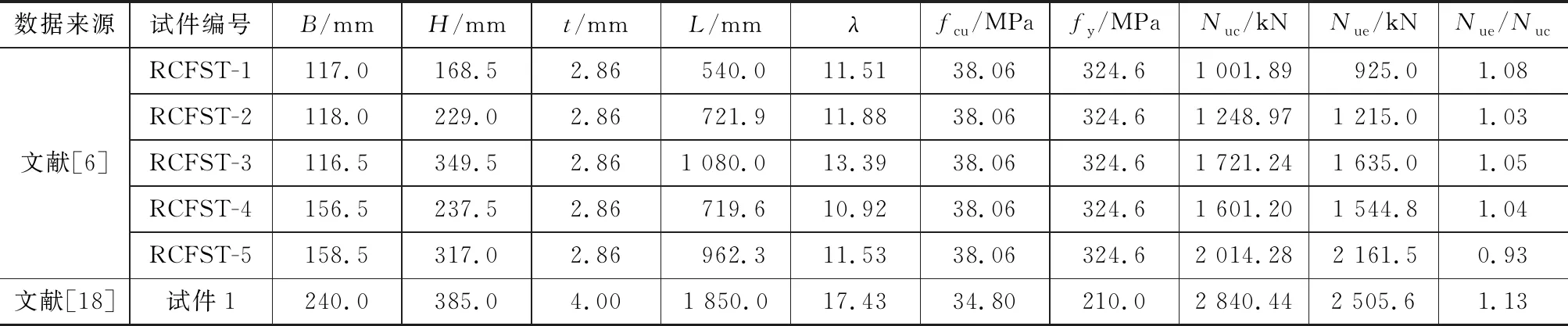
表7试验数据及公式计算结果对比Tab.7Comparison Between Experimental Date and Calculated Results by Formula

(2)分析中长柱与长柱的破坏模式、应力-应变关系曲线得出不同长细比构件的破坏模式，可知中长柱与长柱的界限长细比λp=86.4～96.0。

(3)圆端形钢管混凝土中长柱的极限承载力与长细比呈负相关，与钢材强度、钢管厚度呈正相关，混凝土强度的变化对承载力的影响不大。

(4)通过分析长细比与稳定系数的关系可知短柱与中长柱的界限长细比λ0=10～11，该结果与方形、矩形钢管混凝土柱界限长细比公式较吻合，故方形、矩形钢管混凝土柱界限长细比公式适用于圆端形钢管混凝土。

(5)提出了圆端形钢管混凝土长柱轴压极限承载力简化计算公式，并验证了公式的准确性。该成果可为圆端形钢管混凝土长柱构件轴压与偏压设计提供参考依据，并为工程实际应用提供理论指导。