基于Q学习的单路口交通信号协调控制

胡 宇，刘美玲，周子昂，张 敏

(东北林业大学信息与计算机工程学院，黑龙江 哈尔滨 150040)

0 引 言

近年来，随着城市化趋势日益明显，城市化所带来的问题也渐渐地显露出来。交通堵塞便是这些问题中的一个。而交通的拥堵对于城市的发展有着巨大的影响[1]。如何解决交通拥堵成为各大城市急于解决的问题之一。

平面交叉口通行能力不足是造成交通拥堵的主要原因，由于单路口作为城市交通体系中的基本节点，因此对于单路口交通信号控制优化可以更加有效地缓解城市局部交通拥堵。城市中单路口的车流量为动态数值，而国内对于交通信号的控制多采用固定时间控制法，因此任何预定义的交通信号都不能很好地适应实际情况从而不能使单路口的交通性能达到最优，严重的则会造成交通拥堵。

由于定时信号控制不能很好地适应当前交通量而导致损失部分资源，同时随着计算机及其硬件的飞速发展从而对于道路数据的测量变得越来越容易[2-3]，因此科研人员提出了利用机器学习对交通信号进行自适应控制[4-6]。

许多科研工作者针对此问题展开了多方面的研究。英国学者Watkins[7]提出了强化学习后，美国学者Thorpe[8]率先将强化学习与交通信号控制相结合，通过神经网络来控制优化信号灯时长。加拿大学者Abdulhai等人[9]以车辆排队长度作为成本函数，应用Q学习对单路口信号灯时长进行优化。同时国内的学者刘成健等人[10]对当前交通参数模糊化处理，将排队长度以及车道繁忙度建模后作为成本函数并实现了检验。卢守峰等人[11]以进入交叉口排队长度最小为优化目标，对Q学习在交叉口控制效果实现了检验。徐勋倩等学者[12]利用蚁群算法实现了一个单路口交通信号实时控制的方案。赵晨等学者[13]对单路口车流量利用模糊逻辑对其进行分类并设定当前相位的最短绿灯时长，然后根据当前相位不同的车流量增加相应的绿灯时长，从而实现对路口车流量的动态控制。赵晓华、高丽颖等学者[14-15]通过BP神经网络实现利用Q学习对信号控制的方法并且提出了一种新的交通控制奖惩函数。沈文等人[16]以车均延误作为成本函数，通过Q学习对单路口信号灯控制进行优化。但笔者认为单独针对车均延误优化只针对了时间上的损耗进行最优化处理而忽视了汽油的消耗等经济上消耗，比如每年由于交通拥堵所造成的损失以北上广为例达到了1600亿元人民币。

由此，笔者认为SCOOT系统——一种上世纪研发但现今依然在使用的交通控制系统中对于路口的优化参数的设定更加贴近现实情况，同时人们又可以通过此系统经过这么长时间的使用而并未被淘汰的情况可以看出此种方法的实用性。同时，SCOOT系统中将地图中每个路口作为节点，在每个信号周期内，根据到达节点交通需求变化来对每次绿灯时长变化进行调整。这种单路口的节点与Q-learning算法的单路口agent相似。因此，本文结合SCOOT交通系统中对绿信比优化采用停车次数与车均延误率相结合的思想来建立新的模型，并将其作为成本函数代入Q学习算法中对单路口绿信比进行优化。

本文将车均延误与单路口中的停车次数相结合，以此为成本函数，通过建立适应交通信号控制的奖惩函数模型，详细介绍Q学习算法应用在单路口的信号控制过程，最后分析与Webster配时算法和单独针对车均延误的Q学习的优化效果。

1 Q学习

Q-learning[17-18]是强化学习算法中value-based的算法，是强化学习中最为重要的算法之一。Q即为Q(s,a)，是在某一时刻的s状态下(s∈S)，采取动作a(a∈A)能够获得收益的期望。环境会根据agent的动作反馈相应的回报rewardR，所以算法的主要思想是将State与Action构建成一张Q-table来存储Q值，然后根据Q值来选取能够获得最大收益的动作。

感受与效应装置是用于接收感知外界因素并选择相对应的处理机制的实体。处理机制输出相应的回报函数刺激外界因素再输出新的状态。

在原始状态s的基础上接受外界因素，即动作a，然后通过处理机制寻找最大回报值。

可得到以下公式：

Qt(s,a)←Q(t-1)(s,a)+α[R(s,a)+γmaxQ(t-1)(s′,a′)-Q(t-1)(s,a)]

可以通过控制折扣因子γ来得到最优解。由于折扣因子γ∈[0,1]，当γ接近于1时函数考虑将来回报，而当γ接近于0时，则考虑即刻回报。

Q学习算法步骤[19-20]如下：

1)设置参数α、γ；

2)建立初始化矩阵，即Q(s,a)为初始方案的延误率指标；

3)循环重复计算；

4)获取初始状态s并选取动作a；

5)执行动作a并通过公式得到即刻回报R(s,a)，获得下一状态s′；

6)用新的s′替代原s值；

7)当Q值变大时，停止学习。

2 结合停车次数与车均延误率的Q学习

2.1 综合延误

1)车均延误时间(d)。

根据过渡函数曲线理论[21]，车辆经过一个路口的延误时间包括3部分，即正常相位延误、随机延误及过饱和延误。由此得各相位每辆车的平均延误为：

其中：

x为车辆饱和度，c为信号周期时间，C为通行能力。

每周期每辆车的平均延误为：

2)停车次数[22](h)。

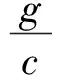
2.2 奖惩函数

Q学习中，Q值的确定与奖惩函数的选择息息相关，因此，奖惩函数的建立十分关键。本文选取停车次数与Webster算法中的d值作为变量建立函数：

当d为定值时，h越大，R(s,a)就越小，当前所得值与Webster值相比差距不大时返回一个相对小的数值；而当前所得值与Webster值相比差距较大时返回一个更加贴近1的值。通过此连续函数，使返回值更加均匀而不会出现离散值；当出现一种相对合适的动作时有可能会直接确定而返回。

2.3 成本函数

成本函数S的物理意义：由于延误率和停车次数为单调函数，因此S也为单调函数，当S越小，表明当前相位的时间和金钱消耗越小，反之，越大。

成本函数公式如下：

3 算例分析

3.1 数据预处理

实验初始配时方案采用Webster配时法，设定车辆的运行速度为6 m/s，制动时间为2 s，黄灯时长为3 s。设定5组实验数据，如表1所示。

表1 各路口车流量

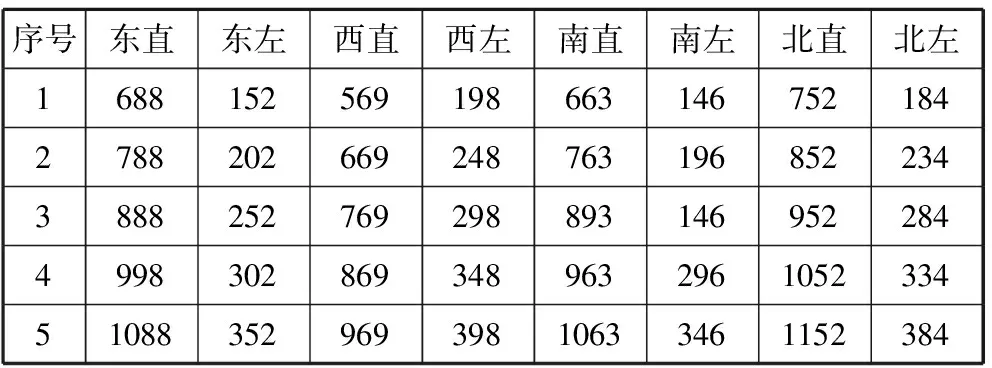
序号东直东左西直西左南直南左北直北左168815256919866314675218427882026692487631968522343888252769298893146952284499830286934896329610523345108835296939810633461152384

实验计算中所用参数α取0.8,γ取0.99。Q学习中初始的配时方案由Webster配时法得出为(34,23,36,22)[23]。

3.2 动作集

Q学习是通过将未来状态可获得的最大奖励添加到实现其当前状态的奖励来实现这一点，从而通过潜在的未来奖励有效地影响当前行动。该潜在奖励是从当前状态开始的所有未来步骤的奖励的预期值的加权和。而每次更新所选取的未来状态便是动作集，即未来所有可能发生的动作或状态。

本次实验的动作集是由a0(34, 23, 36, 22)为初值并与(2,-2, 0)这3种情况进行排列组合，从而得到45种离散型数据集。该动作集是由一定的顺序一一列举出来的，以整数位取值的离散型变量。

在Q学习方案中，4个相位的动作集采用3种可能(2,-2, 0)。经过分析计算得出共有45种方案，计算过程如下：

例如：a1(34,23,36,22),a2(28,25,38,24), …。其中，所有的动作集同时保持总周期不变。得到45个动作集，如表2所示。

表2 动作集

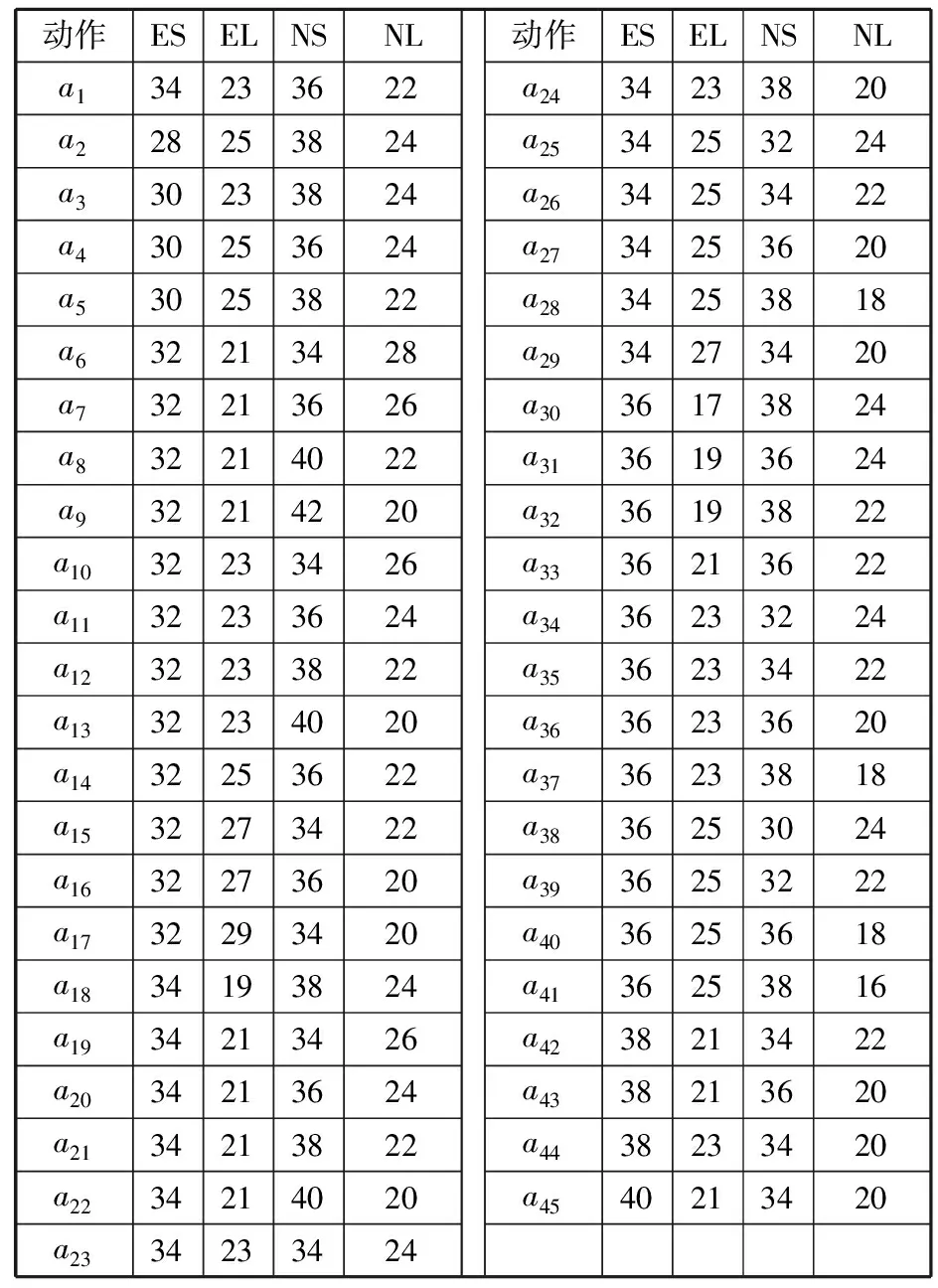
动作ESELNSNLa134233622a228253824a330233824a430253624a530253822a632213428a732213626a832214022a932214220a1032233426a1132233624a1232233822a1332234020a1432253622a1532273422a1632273620a1732293420a1834193824a1934213426a2034213624a2134213822a2234214020a2334233424动作ESELNSNLa2434233820a2534253224a2634253422a2734253620a2834253818a2934273420a3036173824a3136193624a3236193822a3336213622a3436233224a3536233422a3636233620a3736233818a3836253024a3936253222a4036253618a4136253816a4238213422a4338213620a4438233420a4540213420

Q式子更新采用：

Qt(s,a)←Q(t-1)(s,a)+α[R(s,a)+γmaxQ(t-1)(s′,a′)-Q(t-1)(s,a)]

3.3 Q学习优化综合延误率计算

3.3.1 第1时间段

初始配时方案为a0(34, 23, 36, 22)。Q值Q学习第1时间段内综合延误d、奖惩函数R、Q值的计算结果如表3所示。

表3 第1时间段结果

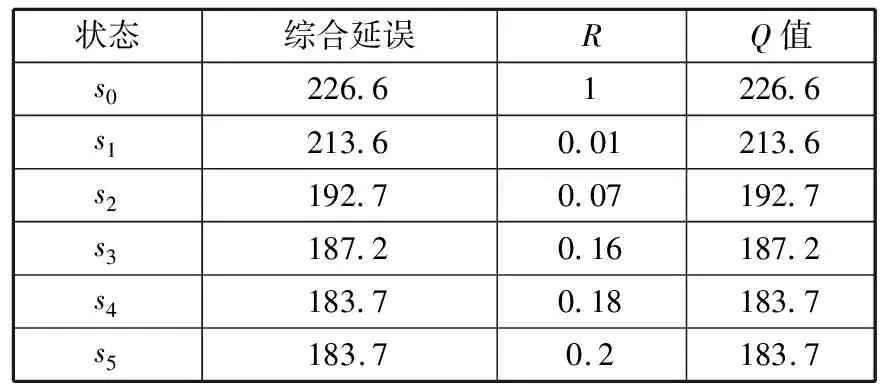
状态综合延误RQ值s0226.61226.6s1213.60.01213.6s2192.70.07192.7s3187.20.16187.2s4183.70.18183.7s5183.70.2183.7

根据表3，贪婪选择最小Q值为183.7，对应方案为(12, 25, 12, 25, 54, 24, 54, 24)，综合延误为183.7。

3.3.2 第2时间段

初始配时方案为a0(34, 23, 36, 22)。Q值Q学习第2时间段内综合延误d、奖惩函数R、Q值的计算结果如表4所示。

表4 第2时间段结果

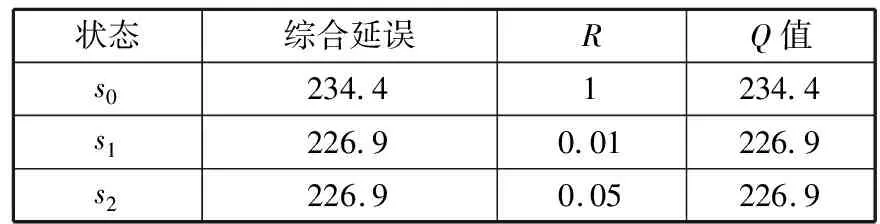
状态综合延误RQ值s0234.41234.4s1226.90.01226.9s2226.90.05226.9

根据表4，贪婪选择最小Q值为226.9，对应方案为(38, 27, 38, 27, 26, 24, 26, 24)，综合延误为226.9。

3.3.3 第3时间段

初始配时方案为a0(34, 23, 36, 22)。Q值Q学习第3时间段内综合延误d、奖惩函数R、Q值的计算结果如表5所示。

表5 第3时间段结果

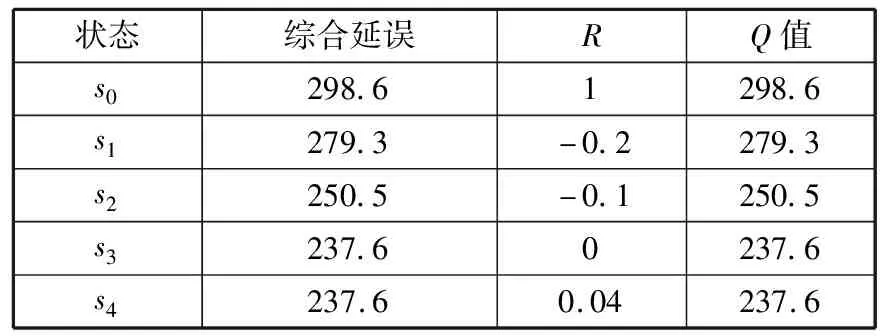
状态综合延误RQ值s0298.61298.6s1279.3-0.2279.3s2250.5-0.1250.5s3237.60237.6s4237.60.04237.6

根据表5，贪婪选择最小Q值为237.6，对应方案为(24, 27, 24, 27, 32, 32, 32, 32)，综合延误为237.6。

3.3.4 第4时间段

初始配时方案为a0(34, 23, 36, 22)。Q值Q学习第4时间段内综合延误d、奖惩函数R、Q值的计算结果如表6所示。

表6 第4时间段结果

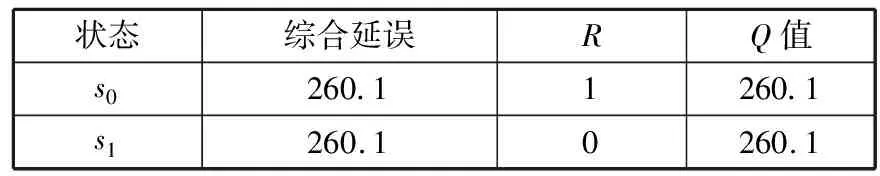
状态综合延误RQ值s0260.11260.1s1260.10260.1

根据表6，贪婪选择最小Q值为260.1，对应方案为(34, 23, 34, 23, 36, 22, 36, 22)，综合延误为260.1。

3.3.5 第5时间段

初始配时方案为a0(34, 23, 36, 22)。Q值Q学习第5时间段内综合延误d、奖惩函数R、Q值的计算结果如表7所示。

表7 第5时间段结果

状态综合延误RQ值s0320.31320.3s1346.1-0.2346.1s2312.9-0.2312.9s3312.9-0.2312.9

根据表7，贪婪选择最小Q值为312.9，对应方案为(30, 23, 30, 23, 40, 22, 40, 22)，综合延误为312.9。

3.4 新老算法对比

各个时间段Q学习控制模型与Webster模型所对应的综合延误对比，详见表8。

表8 与Webster的对比

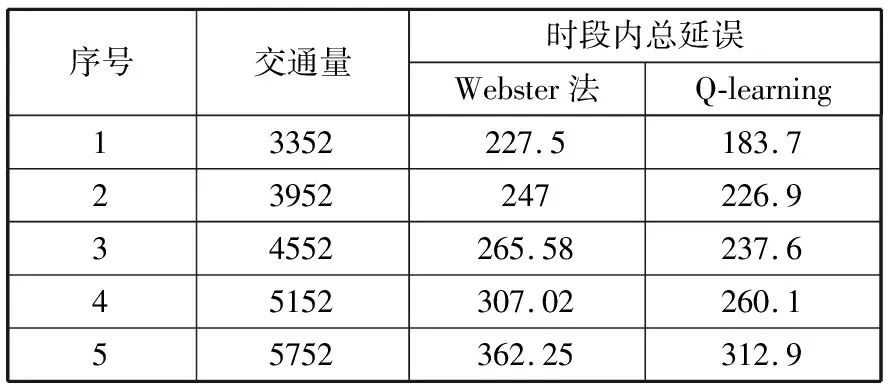
序号交通量时段内总延误Webster法Q-learning13352227.5183.723952247226.934552265.58237.645152307.02260.155752362.25312.9

各个时间段中，使用只针对车均延误率的Q学习算法和结合SCOOT系统绿信比优化方法的Q学习算法两者相对于Webster算法的优化百分比如表9所示。

表9 与车均延误率算法的对比

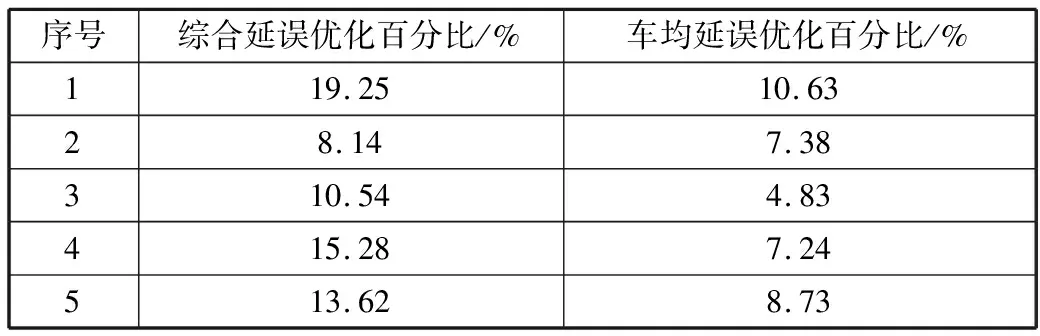
序号综合延误优化百分比/%车均延误优化百分比/%119.2510.6328.147.38310.544.83415.287.24513.628.73

由表9可以得出，与未经改进的车均延误率的传统算法对比，新的算法效率普遍提高了0.76～8.62个百分点，效果较为显著。

如图1与图2所示，在将传统定时控制的Webster算法作为Base Line来对基于车均延误的Q学习算法与结合SCOOT系统优化思想的Q学习进行比较，可以看出无论是当前车流量接近饱和流量还是当前路口的车流量与饱和流量相差较多的情况下都优于基于车均延误的Q学习。

这说明将SCOOT绿信比优化方法引入与Q学习相结合的算法对单路口的绿信比配时优化更加有效，更加有助于拥堵或非拥堵路段的路口车流通行。

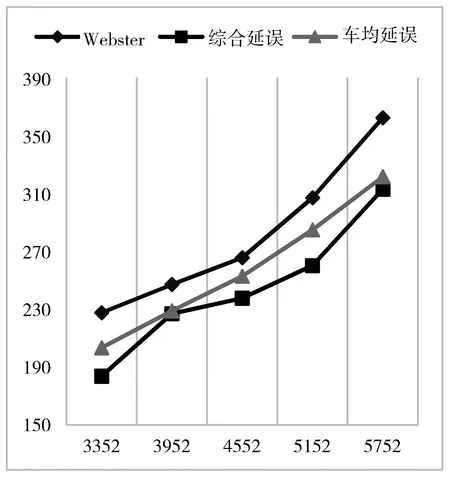
图1 各算法之间结果对比

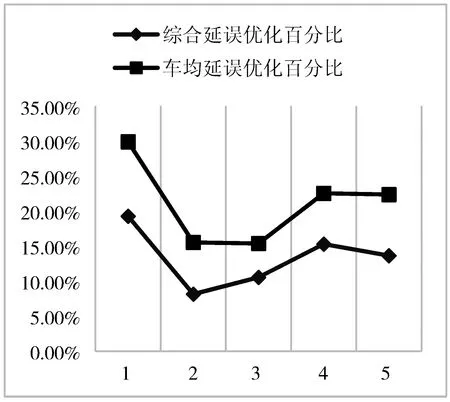
图2 2种算法优化比率对比

4 结束语

城市路口绿信比配时的动态控制是时代发展的趋势，本文的算法就是一种有效的优化方法。本文通过结合经典的SCOOT系统中对绿信比优化的思想，重新定义Q学习中的成本函数和奖惩函数并扩大了Q学习算法学习过程中的动作集，在普遍只针对延误率等时间因素的成本函数上融入了类似SCOOT系统中的停车次数等消耗因素使函数更加贴近生活实际，且提高了优化效率，一定程度上完善了Q学习的成本函数，使其更加具有实际性和现实性。在构造奖惩函数的过程中采用连续函数，使在函数逼近的过程中增加了算法的有效性和准确性，防止单一正反馈一直递增。为了使单路口所选取的配时动作更加有效，扩大了动作集，使Q学习在学习过程中具有更多的选择，使得到的最终结果更加贴近实际。

本文充分地将SCOOT系统中对绿信比优化的方法与强化学习中的Q学习算法相结合，将经典的算法与当前的新方法相结合，使路口绿信比更加贴近车流量情况，使其在当前时间段内可以通过更多的车辆，由此缓解路口的拥堵情况。

本文将前人对单路口绿信比优化的方法与强化学习等新兴计算机技术相结合，对于建立智慧城市交通，缓解城市的区域交通拥堵有着较强的推动力。

基于本文基础，下一步将对不定时长的信号灯周期进行建模，尝试解决在没有已定动作集的情况下，通过算法自动得出最适用于当前情况的配时方案。同时，改进算法使其可以同时优化多个路口，在一定区域内达到更加快速地舒缓交通，避免拥堵。