一种弧齿锥齿轮弯曲疲劳寿命仿真与加速试验

郭玉梁，魏冰阳，李智海，孟 洋，张 柯，刘大可

(1.河南科技大学 机电工程学院，河南 洛阳 471003；2.佛罗里达理工学院 工程与科学学院，佛罗里达 墨尔本 32901)

0 引言

弧齿锥齿轮在机械传动领域应用广泛[1]，在实际使用中，齿轮构件的失效会导致整个传动系统的失效[2]。弧齿锥齿轮是各种机械设备中的重要零件[3]，其轮齿弯曲疲劳引起的断裂可能产生灾难性的后果，故其疲劳寿命的预测与评价研究尤为重要。弧齿锥齿轮齿根断裂多为高周疲劳破坏，而高周疲劳试验需要大量的试样，试验周期长、耗费大。有限元疲劳寿命仿真与加速试验方法，可大幅缩减试验成本与研发周期，但加速疲劳试验在弧齿锥齿轮中尚无广泛应用，相关资料匮乏。

有限元疲劳寿命仿真与加速试验在其他种类零件中已有研究和应用。文献[4]对蜗杆传动进行了疲劳寿命仿真，并对蜗杆副的加速疲劳试验方法进行了研究。文献[5]研究了变速器的加速疲劳试验。文献[6]研究了矿用减速机的加速疲劳寿命试验。文献[7]研究了圆柱齿轮的弯曲疲劳损伤。文献[8]研究了聚酯纤维缆的疲劳损伤。本文在上述研究成果的基础上，参考齿轮弯曲疲劳强度试验方法[9]，设计了一对20CrNiMo材料弧齿锥齿轮，对其进行了瞬态动力学有限元分析。使用疲劳分析软件nCode对锥齿轮副进行了疲劳寿命仿真。采用罗卡提(Locati)方法阶梯增载进行了疲劳寿命加速试验，验证了疲劳寿命仿真与加速试验方法的可行性，为弧齿锥齿轮的疲劳寿命评价提供了一种有益的借鉴。

1 弧齿锥齿轮三维建模及模拟装配

根据齿轮弯曲疲劳强度试验标准[9]，设计了一对试验弧齿锥齿轮。由格里森程序计算其几何参数，结果如表1所示，其加工参数如表2所示。在格里森磨齿机上进行磨齿加工，测量齿轮精度的各项指标不低于5级。

根据齿轮啮合原理[10]，利用MATLAB软件编制了弧齿锥齿轮齿面点的求解程序。使用Unigraphics NX(以下简称UG)软件构建了试验弧齿锥齿轮的精确三维模型，对齿轮副进行几何模型简化，并对轮齿切分。弧齿锥齿轮装配模型如图1所示。

使用UG软件进行模拟滚检，接触斑点的大小和位置符合要求[11-12]，弧齿锥齿轮模拟滚检示意图如图2所示。试验弧齿锥齿轮实际装配并涂色滚检[13]，齿面接触区如图3所示。模拟滚检与实际装配涂色滚检得到的接触斑点相近。三维建模时，按照实际试验弧齿锥齿轮的齿根圆角半径建立齿根过渡曲面，以便能够最真实地模拟齿根实际工作应力场状况。

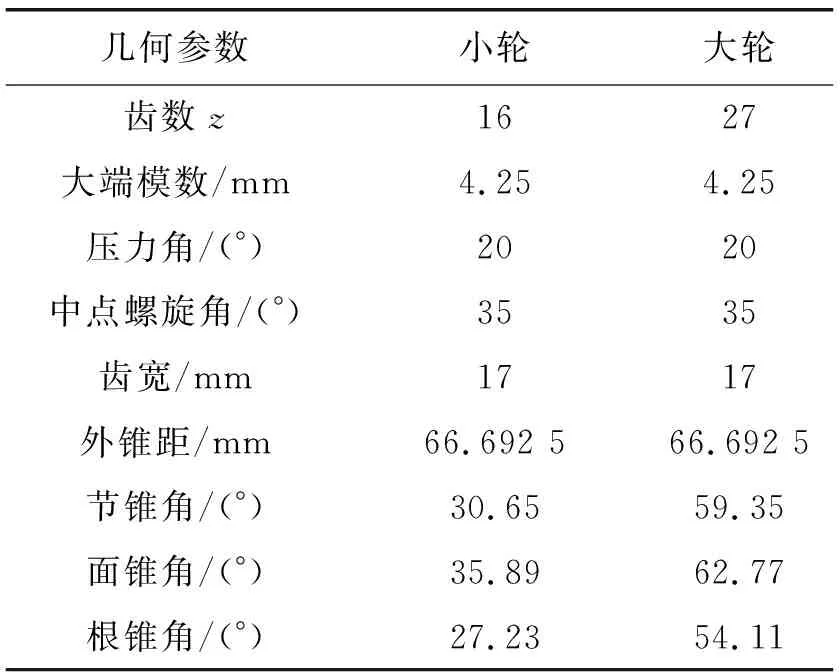
表1 弧齿锥齿轮几何参数

表2 弧齿锥齿轮加工参数

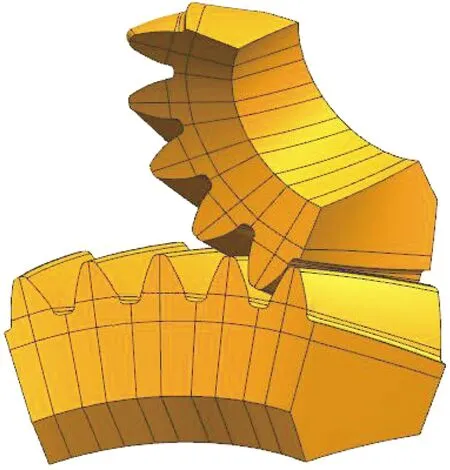
图1 弧齿锥齿轮装配模型

图2 弧齿锥齿轮模拟滚检示意图

图3 齿面接触区

2 瞬态动力学有限元分析

进入ANSYS Workbench软件界面，将弧齿锥齿轮装配三维模型文件导入瞬态动力学分析。

本文大、小轮的材料均采用20CrNiMo，该材料对应的美国标准牌号为SAE Steel Grade 8620。将该材料从nCode材料库中导入Workbench，可使瞬态动力学有限元分析与疲劳寿命仿真材料一致。进入model模块，将大轮与小轮的材料设定为SAE Steel Grade 8620。

接触面选择小轮全部齿面，目标面选择大轮全部齿面，接触类型选择有摩擦接触Frictional，摩擦因数输入0.03，并分别在大小轮的内圈位置设置旋转运动副。对所有实体使用多域扫掠方式进行网格划分，结果如图4所示。

通过相关经验与计算公式，大致推断循环次数为3×106左右时小轮受到的扭矩为400 N·m。在进行齿轮寿命试验时，小轮转速为600 r/min。以该边界条件为例，设定大轮旋转运动副加载类型为扭矩，输入400 N·m；设定小轮旋转运动副加载类型为转速，输入600 r/min。

在分析设置中设置运动时间为0.025 s，运算步数为100，保证5个齿完整的啮合运动过程。求解后，察看小轮，齿轮等效应力云图如图5所示。后期根据疲劳寿命仿真结果，使用逐次逼近法调整扭矩值。

图4 网格划分结果

图5 齿轮等效应力云图

3 弯曲疲劳寿命仿真

将不同转矩下的瞬态动力学分析与疲劳寿命仿真软件nCode建立连接，nCode读取瞬态动力学中每个网格单元在整个时间历程中的应力值，用来计算每个网格单元的寿命。

3.1 材料属性设置

在求解器上右键点击并选择Material load选项，进入材料设置，由于nCode提供的20CrNiMo的应力-疲劳寿命循环次数(S-N)曲线为应力比S-N曲线，所以材料类型选择多应力比S-N曲线，将所有实体的材料设置为SAE Steel Grade 8620。

3.2 分析引擎设定

为了与材料类型对应，选择应力寿命方法为多应力比曲线。平均应力修正方法选择插值法，并输入寿命仿真的存活率。

3.3 疲劳寿命仿真结果及分析

为得到试验锥齿轮的存活率-应力-疲劳寿命循环次数(P-S-N)仿真曲线，在一定存活率下至少应仿真出2个数据点，确定P-S-N曲线的拐点和斜率。本文以循环次数3×106对应的弯曲应力值为齿根弯曲疲劳极限，循环次数大于1×103产生的疲劳为高周疲劳，在不同存活率下，仿真得到这2个循环次数对应的齿根弯曲应力值。

对于弧齿锥齿轮副，工作面为小轮凹面[14]，该侧齿根受拉应力，凸面齿根受压应力。齿轮材料的抗拉强度要明显弱于抗压强度，弧齿锥齿轮运行中，轮齿一般从小轮凹面齿根处疲劳断裂。因此，最终结果查看小轮第3轮齿凹面齿根弯曲应力值与疲劳寿命循环次数。

全部设置完成后点击运行即可进行疲劳寿命仿真。经若干次修正大轮扭矩值、多次有限元计算与疲劳寿命分析后，逼近循环次数3×106的弯曲疲劳寿命，分别完成存活率为95%、97%和99%的弯曲疲劳寿命仿真，结果如表3所示。同样方法，完成循环次数约1×103的弯曲疲劳寿命仿真，结果如表4所示。

表3和表4中循环次数均为小轮第3轮齿凹面齿根最少弯曲疲劳寿命对应的循环次数，弯曲应力σF均指该位置齿根弯曲应力最大值。

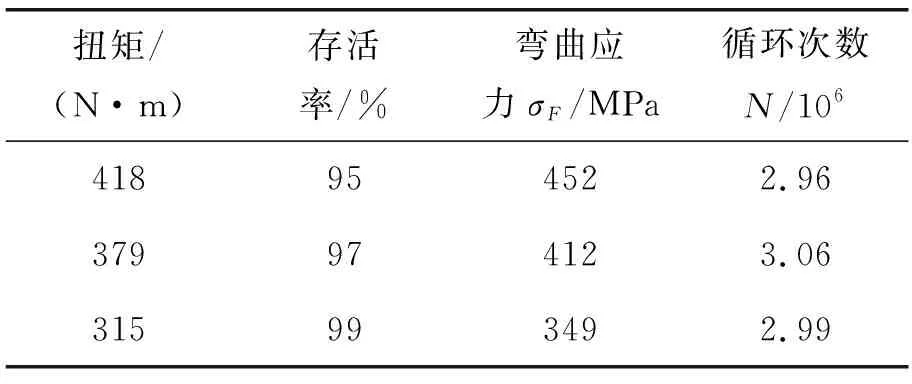
表3 循环次数约3×106的弯曲疲劳寿命仿真结果

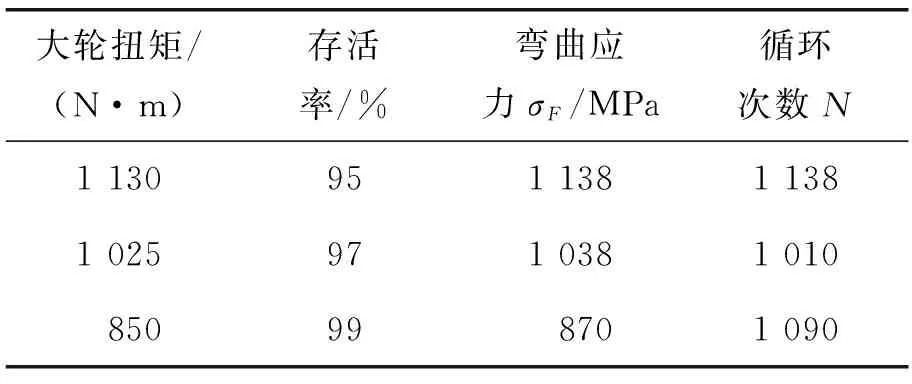
表4 循环次数约1×103的弯曲疲劳寿命仿真结果

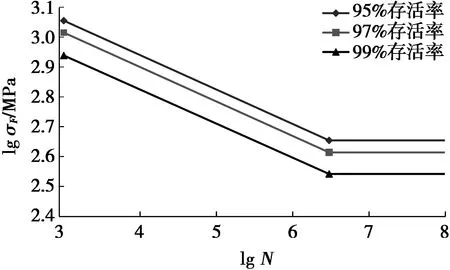
图6 齿轮仿真P-S-N曲线

在双对数坐标系下，根据表3和表4中6个数据点，绘制存活率为95%、97%和99%的3条齿轮仿真P-S-N曲线，如图6所示。

4 齿根弯曲疲劳加速试验

4.1 锥齿轮弯曲疲劳极限应力快速测定法

本文基于迈因纳(Miner)线性损伤累计理论，采用Locati方法对齿根弯曲应力阶梯增载，通过数据处理，快速得出所测齿轮的疲劳极限应力值[15]。

假设零件在应力σi下疲劳寿命的循环次数为Ni，Miner法则认为当零件循环次数ni达不到Ni时，每次循环造成部分寿命损伤，ni次的损伤率为ni/Ni，损伤累积到(n1/N1)+(n2/N2)+……+(nn/Nn)=1，即损伤率之和∑(n/N)=1时，产生疲劳失效。

基于这一原理，Locati方法可以用一个试件完成零件的疲劳寿命试验。试验时应力阶梯增载，即△σ=σ2-σ1=σ3-σ2=…=σi-σi-1。在每一应力下运转次数一致。

应力阶梯与循环周次之比△σ/n称为循环比率，一般取△σ/n≈2×10-4，初应力取值略低于预估疲劳极限σlim。

在进行数据处理时，先假设3条σ-N曲线及对应的疲劳极限值σlim。计算出3条σ-N曲线的∑(n/N)值，根据3个∑(n/N)值和对应的疲劳极限值σlim，绘制出一条∑(n/N)-σ曲线，根据该曲线插值找出∑(n/N)=1时的疲劳极限应力值σlim。

4.2 加速疲劳寿命试验

理论上疲劳寿命仿真结果与试验结果接近，故根据第3节的疲劳寿命仿真结果取得3条参考曲线。

S-N曲线的幂函数公式为σmN=C，其中，σ为应力；N为疲劳寿命循环次数；C为材料常数。

第1条采用95%存活率曲线，齿根弯曲疲劳极限应力σFlim1=452 MPa，疲劳极限的循环次数N0=3×106，则：

本文选择2条次要参考曲线，齿根弯曲疲劳极限应力σFlim2=430 MPa、σFlim3=470 MPa，曲线斜率和疲劳极限的循环次数均保持不变，仅极限应力变化，故：

对于这3条曲线，任意弯曲应力σ对应齿轮弯曲疲劳寿命的循环次数(以下简称弯曲应力对应寿命)为：

N1=C1/σ8.671=3.161 0×1029/σ8.671；
N2=C2/σ8.671=2.050 8×1029/σ8.671；
N3=C3/σ8.671=4.434 9×1029/σ8.671。

试验设备采用机械式锥齿轮闭功率流试验台[16]，如图7所示。

若试验中发生齿根处出现疲劳裂纹、载荷降低5%～10%及轮齿折断这3种情况中的任意一种，便认定弧齿锥齿轮弯曲疲劳破坏失效。

取初始应力σ0=400 MPa，每个载荷等级循环次数n=1.8×105，每次增载40 MPa，循环比率△σ/n=2.22×10-4。试验前轻载运行90 min。试验过程中，保持齿轮润滑油温30～55 ℃，每增载2个载荷等级，更换一次齿轮润滑油。

在弧齿锥齿轮弯曲疲劳寿命试验中，小轮转速600 r/min。当齿根弯曲应力增载到579 MPa，循环次数达到1.26×105时，小轮轮齿发生断齿，如图8所示。

整理试验结果，进行数据处理后如表5～表7所示。

图8 小轮断齿图

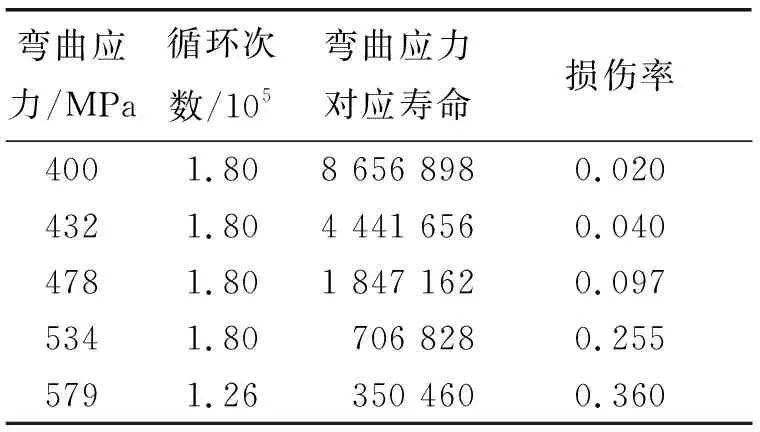
表5 N1曲线试验数据统计表

表6 N2曲线试验数据统计表

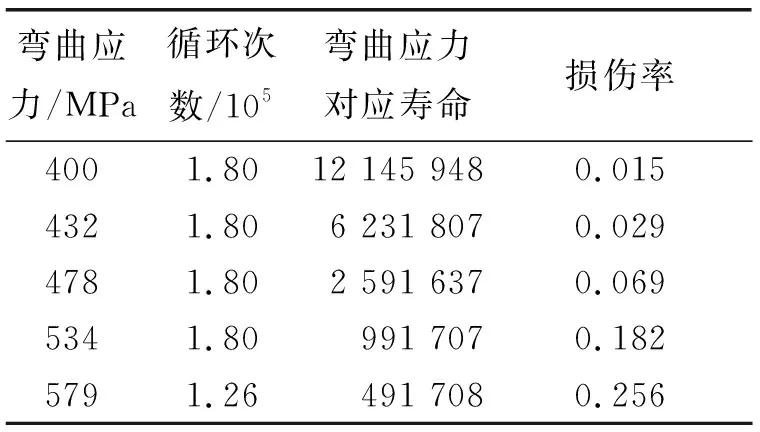
表7 N3曲线试验数据统计表

图9 齿轮∑(n/N)-σ图

由表5得到：以弯曲疲劳极限σlim=452 MPa计算损伤率时，损伤率之和∑(n/N)=0.772。同理，由表6和表7分别得到：σlim=430 MPa时，∑(n/N)=1.188；σlim=470 MPa时，∑(n/N)=0.551。根据这3个数据点可作出齿轮∑(n/N)-σ曲线图，如图9所示。

由图9可得：当∑(n/N)=1时，锥齿轮试件的齿根弯曲疲劳极限应力值为439 MPa，疲劳寿命仿真结果与试验结果误差为3%。

5 结束语

(1)通过nCode软件对20CrNiMo材料弧齿锥齿轮进行了疲劳寿命仿真。依据Miner疲劳损伤累积理论，采用Locati方法对齿根弯曲应力阶梯增载，进行了疲劳寿命加速试验，通过数据处理，快速得出了所测齿轮的疲劳极限应力值，试验结果与疲劳寿命仿真结果具有较高的吻合度。验证了本文所给出的疲劳寿命仿真和加速试验方法的可行性。

(2)本文方法能够为弧齿锥齿轮的弯曲疲劳寿命评价和设计提供有益的借鉴。对缩短齿轮弯曲疲劳寿命台架试验时间、减少试验成本具有重要的工程意义。

由于本次仅做了一对齿轮试验，试验数据可能存在偶然性，作为阶段性成果予以公布。在后续研究中会在此基础上增加试验样本量，使试验数据具有更高的可信度。