(2+1)维Sawada-Kotera方程的complexiton解

张永丽， 孙艳芳， 张辉群

(青岛大学 数学与统计学院, 山东 青岛 266071)

0 引言

由于非线性偏微分方程的精确解，有助于研究者更好地理解方程所描述的物理现象，因此，这方面一直是非线性领域研究的热点之一。随着研究的深入，研究人员已经建立和发展了很多有效的方法[1-7]。应用这些方法，可以得到各种形式的精确解，例如孤立波解、周期波解、lump解和complexiton解等，用于解释原方程所表示的具有不同动力学特点的物理现象。

Complexiton解是由指数函数和三角函数组合的一类特殊的精确解。文献[8]应用Wronskian技术，首次得到了Korteweg-de Vries(KdV)方程的complexiton解。文献[9]利用扩展变换有理函数法得到了几个非线性微分方程的complexiton解。文献[10]应用简化的Hirota双线性方法给出了两个非线性偏微分方程的complexiton解。文献[11]应用线性叠加原则给出了(3+1)维Boiti-Leon-Manna-Pempinelli(BLMP)方程的complexiton解。值得注意的是，对于(1+1)维可积系统，如KdV系统，大多数已知的complexiton解都是奇异的。一般地，在物理应用方面更需要的是寻找非奇异解[12-14]，因此，正complexiton解的研究具有物理应用价值。目前，正complexiton解的求解方法是线性叠加原则和Hirota双线性[15-16]。本文利用线性叠加原则和Hirota双线性来研究(2+1)维Sawada-Kotera (SK)方程，获得了方程的共振多波解、complexiton解和正complexiton解，并且利用图像展示出解的一些动力学特征。此外，本文给出的解不仅包含文献[17]中得到的complexiton解，而且更加丰富。

1 (2+1)维SK方程的共振多波解

本文考虑(2+1)维SK方程：

(1)

(2+1)维SK方程(1)是一种B型KP模型[18]，因与B型群有关，也被称为BKP方程，被广泛应用于物理学的许多分支中，例如共形场理论和二维量子重力规范场。当u(x,y,t)=u(x,t)时,(2+1)维SK方程(1)被约化为(1+1)维SK方程[19-20]：

(2+1)维SK方程(1)已被众多学者研究。例如，文献[21]利用Painlevé截断展开法和Hirota双线性方法，展示了方程(1)的多孤子解；文献[22]研究了方程(1)的Bäcklund变换和Lax对；文献[23]结合Hirota双线性形式和一个一般的黎曼θ函数理论，设计了构造方程(1)的双周期波解的直接方法；文献[24-25]利用正二次函数法，得到了方程(1)的lump解。

根据Hirota双线性方法，在变换u=6(lnf)xx下，(2+1)维SK方程(1)具有Hirota双线性形式如下：

(2)

其中：Dx、Dy和Dt是Hirota双线性算子[18]。

(3)

其中：n、m和r为任意非负整数。P是所示变量的多项式，满足：

P(0,…,0)=0。

(4)

对于固定的正整数N,考虑N波变量和指数波函数：

(5)

进而得到指数波函数的线性叠加形式为：

(6)

在f的双线性恒等式条件下得到:

(7)

其中：1≤i,j≤N。显而易见，在式(6)中，指数波函数的线性叠加f是双线性SK方程(2)的解，当且仅当满足如下条件：

(8)

即

(9)

计算式(9)得到：

b1=-1,b2=-9。

(10)

进一步得到波变量

(11)

最后，通过线性叠加原则得到(2+1)维SK方程(1)的共振多波解[17,26]：

u=6(lnf)xx

(12)

其中：

(13)

2 (2+1)维SK方程的complexiton解

当1≤i≤N1时，有线性叠加解：

(14)

满足(2+1)维双线性SK方程(2)。

ϖi，1+iϖi，2，

(15)

其中，ϖi的共轭形式为

(16)

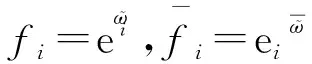
(17)

再次利用线性叠加原则，得到(2+1)维SK方程(1)的复值的complexiton解：

u=6(lnf)xx,

(18)

其中：

(19)

为了得到(2+1)维SK方程(1)的实值的complexiton解，取

(20)

将式(20)代入式(18)和式(19),得到(2+1)维SK方程(1)的实值的complexiton解：

u=6(lnf)xx,

(21)

其中：

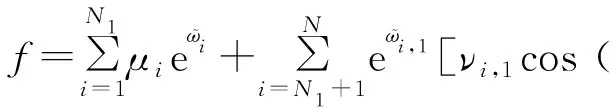
(22)

μi,νi,1,νi,2∈R,ϖi,1和ϖi,2被式(15)所确定。

3 (2+1)维SK方程的正complexiton解

一般地，上述得到的complexiton解(21)具有奇异性。例如，当N1=1,N=2,ϖ>1=0,ϖ>2,1=0,ϖ>2,2=2πk,其中，k1=γ2=0,δ2=2πk,k∈R,ν2,1=-1,u1、ν2,2是任意的实数，在(x,y,t)=(1,0,0)处，complexiton解(21)具有奇异性。

当1≤i≤n时，有:

-ϖ>i=(-ki)x-(-ki)3y-9(-ki)5t, 1≤i≤n。

(23)

显然,eϖi和e-ϖi都是双线性SK方程(2)的解。运用线性叠加原则得到：

(24)

是双线性SK方程(2)的实值解。

当n+1≤i≤n+m时，得到：

(25)

如前所述,eϖi和e-ϖi也都是双线性SK方程(2)的复值解。同样运用线性叠加原则，

(26)

是双线性SK方程(2)的实值解。

最后，通过线性叠加原则得到了(2+1)维双线性SK方程(2)的解:

(27)

在式(27)中，取参数n=m=1,k1=1,k2=1,μ1=4,μ2=2,得到(2+1)维SK方程的正complexiton解：

(28)

(a) t=0

(b) t=1

(c) t=2

图1 (2+1)维SK方程的正complexiton解(28)在不同时间的三维图像

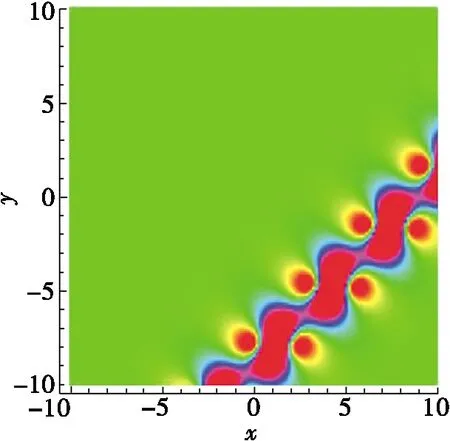
(a) t=0

(b) t=1

(c) t=2

图2 (2+1)维SK方程的正complexiton解(28)在不同时间的密度图像

4 结束语

利用双线性形式的(2+1)维SK方程的多指数波解的叠加，得到了(2+1)维SK方程的正complexiton解，并且通过符号计算验证了所有结果的正确性。构造正complexiton解的关键是采用共轭的复波变量对。利用双线性形式方程具有多波解的叠加现象，得到了正complexiton解。经过研究，这一方法也可应用于(3+1)维potential-Yu-Toda-Sasa-Fukuyama方程等一类非线性偏微分方程。随着广义双线性方程的提出，广义双线性方程的complexiton解将成为下一个研究目标。