高等数学成绩的统计分析

高峥洲 朱永晨 钟丁媛 吴德胜

摘 要：随着大学生活开始，高等数学作为一门新的学科成为了大学生的必修课。如何提高高数成绩成为了大学生和老师最密切关注的问题。我们利用统计学知识对高数成绩进行了一系列的处理，通过观察与分析所给数据，考虑了性别、知识点、专业、学习态度这四个方面的影响因素。利用SPSS、MATLAB等工具，进行分析比较这些因素的重要程度以及影响程度，给出了针对老师和学生群体一系列有依据性的建议，从而希望提高我校学生的高等数学成绩，甚至是提高一点考研率。

关键词：SPSS;高等数学;多元统计分析;聚类分析

一、引言

1.1选题的意义与目的

对于大学生而言，他们不再担心是否需要考得高分，不再会像高中生那样拼命努力的学习。相反，大学自由的生活给了他们懈怠的机会。而在他门面前，高等数学作为一门较有难度的学科，成为他们大学遇到的第一个困难。因此，我们希望通过分析他们的高等数学成绩，来帮助他们在哪方面影响了他们高等数学的学习，给出一些有建设性的建议。希望通过自己的力量帮助他们，为他们尽自己的一份力。

选题的主要目的有3个：

1.通过分析处理数据，给老师和同学们就高等数学学习方面提出一些建议，帮助同学们进步，更希望帮助老师更好的教学。

2.高等数学作为大学学科里较有难度学科的代表，我们分析并给出了一些建议，可以对同学们在今后遇到的有难度的学科有一定的帮助作用。

3.帮助同学们学好高等数学，有利于帮助同学打下信心，为之后的学习打下坚实的基础，更好的体验大学学科的有趣。

1.2高等数学学习的现状

学习高等数学的动机与目的可以直接反映出学生对该课程的学习态度和学习积极性

通过调查，有以下几种情况：

（1）回答“没有兴趣”或“学了没有用处，及格就行”的学生占24.3%。这部分学生的学习目的不明确，学生动机消极，甚至是被迫学习，从而在思想上就对高等数学有抵触情绪，表现为课堂上不愿听课，不认真甚至不做作业，比较懒散，应付考试。其结果往往是考试不及格或成绩不理想，达不到学习的目的和要求。

（2）回答“只需对高等数学有点了解，不必太深”的学生占48.5%。这是因为：一方面，学生毕业后大多从事的是工程技术工作，不是搞数学研究的;另一方面，有不少学生反映高等数学的内容枯燥，公式太多，难度大，因此，不想对高等数学有深入的研究。这是因为高等数学课是在低年级开设的，学生刚从中学升到大学，不少学生仍沿用中学那种“死记硬背”的学习方法，虽然学习较努力，但不理解教学内容，因此，学习仍搞不好。

（3）回答“对高等数学较有兴趣，希望多学一些”的学生占27.1%，这部分学生学习目的明确，求知欲望强烈，能认识到高等数学作为基础课的重要性。

1.3高等数学学习过程的具体表现

高等数学的学习过程对其学习质量起着举足轻重的作用，重视学习过程的引导将得到很好的反馈效果。学习过程包括课前预习、做作业、课后复习等一系列的学习环节。

（1）预习情况。经调查，有10.2%的学生平时坚持预习，60.9%的学生有时间就预习，另28.9%的学生觉得不必预习，没有预习习惯，这一点应引起我们的重视。课前预习，不仅能提高听效率，而且能培养自学与独立思考的能力。

（2）听课情况。经统计，有少数学生不愿意听课占12.3%;大多数学生重视听课，但仍有一些问题存在，如注意力不集中、感兴趣就听等。

（3）作业情况。做作业是进一步消化和吸收课堂所学知识，培养学生逻辑思维能力和运用理论解决实际问题能力的一种方法。经调查，有51.2%的学生能独立认真完成作业;有48.8%的学生存在抄袭作业现象。

（4）复习情况。统计结果表明，在43.2%的学生在做作业前复习，有28.4%的学生采用有时间就复习的策略;有28.4%的学生平时不复习，只在考前突击复习。

二.高等数学成绩影响因素分析

通过从老师那获取的2017至2019的高等数学成绩，我们利用统计学知识对高数成绩进行了一系列的处理，通过观察与分析所给数据考虑了性别、知识点、专业、学习态度这四个方面的影响因素，下面将从这四个角度加以分析。

2.1性别方面

根据图2-1，针对性别因素，男生与女生对于理工科的学习能力本就不太相同，从而会影响最后考试的成绩。因此我们计算高数成绩表格中男女学生成绩的平均值、标准差，绘制得分频数直方图。我们可以看出女生的成绩总体平均值高于男生成绩总体平均值，女生的高分占比也明显避难所多，男生的成绩普遍分布在中等偏下，而女生的成绩普遍分布在中等偏上。

2.2知识点方面

系统聚类法（也称层次聚类法）由于类与类之间的距离计算方法灵活多样，使其适应不同的要求。该方法是目前实践中使用最多的。这该方法的基本思想是：先将个样本各自看成一类，并规定样本与样本之间的距离和类与类之间的距离。开始时，因每个样本自成一类，类与类之间的距离与样本之间的距离是相同的。然后，在所有的类中，选择距离最小的两个类合并成一个新类，并计算出所得新类和其它各类的距离;接着再将距离最近的两类合并，这样每次合并两类，直至将所有的样本都合并成一类为止。这样一种连续并类的过程可用一种类似于树状结构的图形即聚类谱系图（俗称树状图）来表示，由聚类谱系图可清楚地看出全部样本的聚集过程，从而可做出对全部样本的分类。

针对知识点因素，不同的知识点难易程度不同，从而就会导致学生的得分有所差异。首先将所考的高数上下两学期的试卷进行知识点总结，即将每题所考察的知识点罗列处理，再分类匯总，用每项知识点的总得分率作为评判知识点难易程度的指标，然后依次指标运用SPSS进行聚类，得出不同知识点的难易程度图。根据图2-2，可以看出函数的微分、函数在某点的连续性和可导性、最值定理和介值定理这三个知识在所考试卷中最难。

2.3学习态度方面

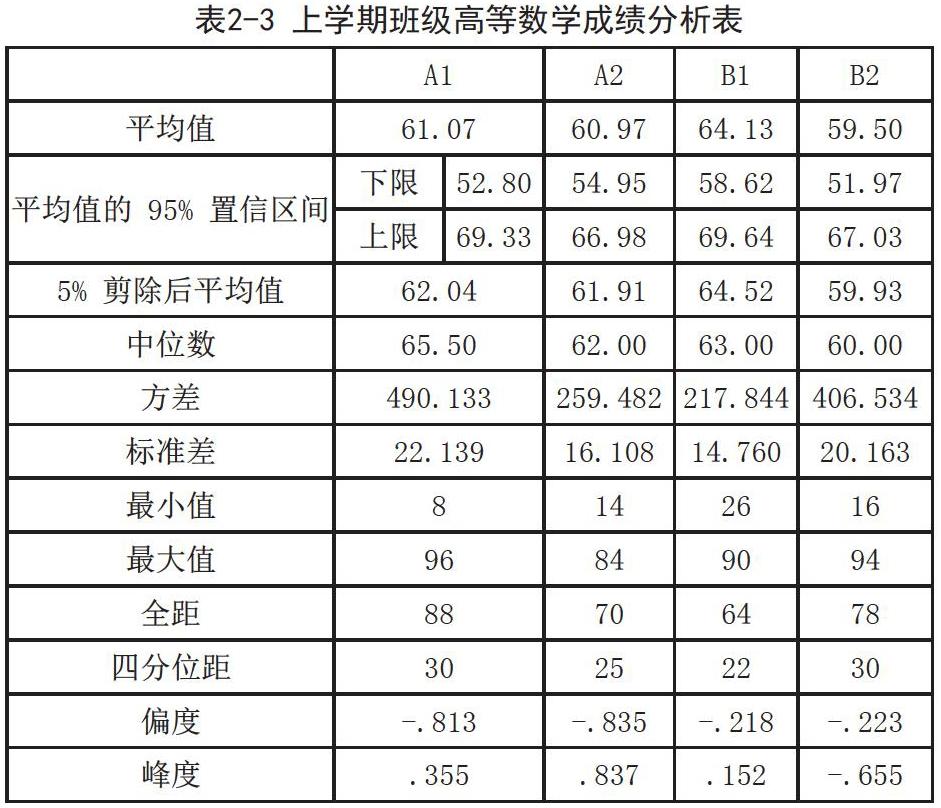
对比表2-3和表2-4，我们发现在经过上半学期的学习过后，下半学期的四个班级的高等数学成绩均有了提高，这反映了在半学期的洗礼下，学生的学习态度有了明显的转变，从而成绩也随之有所提升。

2.4专业方面

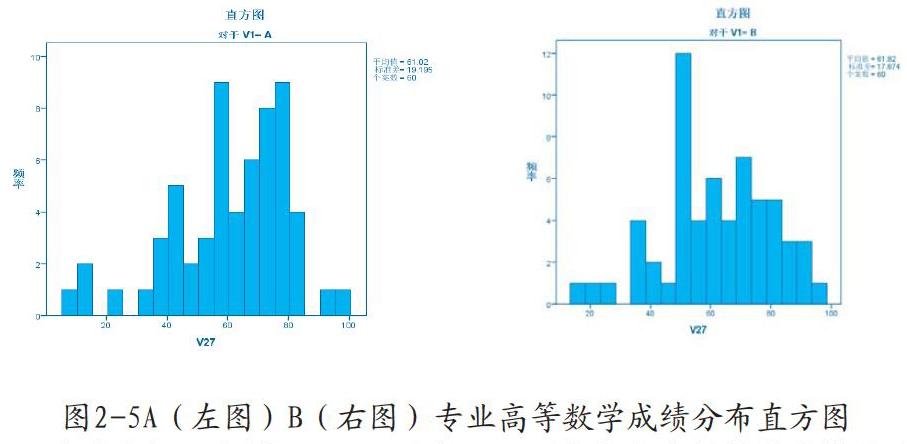
根据图2-5和图2-6，可以发现AB两个专业高等数学成绩分布比较平均，可以推断出两个专业的高数知识掌握要求接近，本质上两个专业大概比较相近。

三.教学方面的建议

3.1给老师的建议

1.应对学生从预习、听课到作业、考试每一环节都严格要求，不能放任自流。同时，应重视高等数学习题的教学。高等数学习题课是课堂教学的进一步深化，作为一个教学环节，对一年级学生是非常重要的，它不仅能够帮助学生复习巩固基本概念，加深理解基本理论，提高解题能力和技巧，而且也给师生提供了一个直接接触的机会，使学生能够在课堂上动手、动脑解决问题，也使教师能了解学生中存在的问题，及时调整教学内容和进度，有的放矢地组织下一阶段的学习。在习题课教学中，可采取多种方法，如教师主讲，进行单向传授;边讲边练，师生共同解题;或让学生讨论，发表自己的观点，教师最后总结。因此，要求教师选好题、备好课，充分估计到学生可能提出的问题及解决方法，以掌握主动权，使教与学真正成为以学生为主的双向活动，取得较好的学习效果。

2.就函数的微分、函数在某点的连续性和可导性、最值定理和介值定理这三个知识进行更加详细细致的讲解。

3.2给学生的建议

1.数据分析发现，一个人的学习态度影响着高等数学成绩。因此，希望同学们可以端正自己的学习态度，秉着一个好学之心，这样成绩自然而然的就会有所提高，学号高等数学也就不在话下了。

2.女生在高等数学的学习过程中，由于女生心细、严谨、认真，所以成绩也比较好。所以建议男生可以多向女生学习，探讨题目。

3.函数的微分、函数在某点的连续性和可导性、最值定理和介值定理这三个知识的得分情况是最糟糕的，建议多花点时间复习理解这三个知识点，多刷一些包含这些知识点的试题，提高自己的理解和应用能力。

参考文献

[1]王航.现代统计分析软件SPSS在学生成绩分析中的应用[J].科技创新导报，2016，13（33）：62-63.

[2]李亚杰.高等院校高等数学课程的成绩分析与评价[J].课程教育研究，2012（05）：9.

[3]陆小华，付申，李媛媛.2003-2004学年高等数学成绩分析[J].北京农业职业学院学报，2004（04）：60-62.

[基金项目]

项目来源：国家自然科学基金面上项目，项目名称：Navier-Stokes-Allen-Cahn方程组的数学理论研究，项目编号：11971234.

项目来源：南京林业大学国际教育学院，项目名称：中外合作办学高水平示范，项目编号：164101005.

项目来源：南京林业大学，项目名称：2017年教学质量提升工程，项目編号：163101812.

项目来源：南京林业大学，项目名称：大学生实践创新训练计划，项目编号：2018NFUSPITP603.

作者简介：

高峥洲（1998.12--），男，汉，广西省北海市人，南京林业大学理学院2017级在读本科生。