基于宏观建模方法的胶合木−钢夹板螺栓连接数值模拟

陈爱军，贺国京，王智丰，王解军

基于宏观建模方法的胶合木−钢夹板螺栓连接数值模拟

陈爱军，贺国京，王智丰，王解军

(中南林业科技大学 土木工程学院，湖南 长沙 410004)

为解决胶合木−钢夹板螺栓连接三维有限元模型计算效率低、收敛性差的问题，采用一种有限元宏观建模方法进行胶合木−钢夹板螺栓连接的模拟，该方法通过非线性一维单元的组合，从而简化连接节点性能的有限元计算。同时，结合胶合木−钢夹板螺栓连接件抗剪性能试验，建立各连接节点的宏观模型和传统三维有限元模型。通过对比试验结果与宏观模型的计算结果，来验证该有限元宏观模型的计算效率及计算精度。研究结果表明：胶合木−钢夹板螺栓连接的宏观模型与连接件抗剪性能试验的荷载−滑移曲线是一致的，该宏观模型能够正确反映胶合木−钢夹板螺栓连接节点的剪切性能、滑移特性、滞回性能、刚度退化和失效特性。相比传统三维有限元计算方法，有限元宏观模型的计算成本相对较低，且收敛性较好。有限元宏观建模方法可有效提高具有大量连接的复杂结构非线性分析的计算效率。

宏观建模方法；胶合木−钢夹板螺栓连接；宏观模型；数值模拟；剪切性能

现代胶合木结构作为一种可再生、低能耗、低排放、环境污染小的新型绿色建筑结构而日益受到人们的青睐。然而，木材既不可像混凝土进行浇筑连接，也不能像钢材通过焊接连接，所以，胶合木结构是具有大量连接的复杂结构[1−3]。其连接的结构性能和失效机理在木结构机制中均发挥了关键性作用[4−5]，因此，在木结构数值模拟计算中必须考虑其连接问题[6−7]。而木材连接部位复杂，在实体单元有限元分析时，会面临计算效率低、收敛性差等诸多问题。既有研究对不同类型的木材连接及材料组合进行了数值模拟[8−9]，研究发现使用三维模型进行螺栓及木材节点的模拟比二维计算方法更加准确。为了进行更加细致的仿真分析，还应考虑几何、接触和材料非线性、节点滑移及木材断裂等[10−11]因素，但多因素的加入严重影响了程序的计算效率与收敛性能，这使得三维实体有限元模型在涉及多连接的结构计算中受到诸多限制，所以，为方便木结构销栓连接的数值计算，有必要建立一种简化的有限元模型。最初的简化模型是使用一维元素来表示销栓连接(如钉子、螺栓或螺钉)，然后对木材及所连接构件进行二维或三维离散化[12]。其中，Meghlat等[13]利用ABAQUS有限元软件开发了一种梁单元，仅通过定义单元的平动自由度就可以模拟木材间栓钉连接节点的力学性能。但此模型仅考虑了弹性阶段木材及连接件的抗剪性能，未计入连接件不同受力状态弹簧单元的本构关系，所以无法模拟其非线性及连接件的滞回性能。同时，也有学者对滞回性能的简化模型进行了相关研究，其大多采用不同本构关系的弹簧单元进行组合，形成一维销栓连接的有限元宏观模型。其中，Blasetti等[14]使用该方法给出了栓钉连接二次循环的本构关系，也考虑了栓钉与木材间出现脱开后重新接触时，荷载−滑移曲线出现的捏缩效应，且此时栓钉的刚度也有所增加。然而，该模型未能模拟栓钉连接的失效状态，仅能反映该连接非线性的弹塑性性能，即随着栓钉连接件荷载的增加，构件刚度不断下降但不出现破坏。本文在开展胶合木−钢夹板螺栓连接剪切性能研究的基础上[15−18]，通过对比分析宏观模型计算结果与试验结果，采用一种简化有限元宏观建模方法[19]，该方法同样既可表示胶合木−钢夹板螺栓连接在荷载作用下的刚度退化，还可表示在其连接到达极限载荷后，螺栓将进入失效状态。该方法大大降低了传统有限元实体模型所需的建模计算成本，提高了胶合木结构螺栓连接的计算效率，为胶合木结构螺栓连接的计算带来了便利。同时，为有限元宏观建模方法应用于胶合木结构螺栓连接的实际工程计算，特别是多螺栓和群螺栓连接的计算提供理论依据。

1 有限元宏观模型

有限元宏观模型是由不同属性的弹簧单元(弹簧、摩擦滑动力和滑动间隙)并联构成，并以该并联单元表示钢夹板螺栓连接的受力性能与滑移特性。模型中并联单元的每一个分支由1个一维的弹簧单元组成。本文采用ANSYS中COMBIN40[20]弹簧单元进行各分支单元的模拟。

该弹簧单元的并联结构为：1)弹簧滑动器，由界限滑移力slide与弹簧组成1；2) 弹簧2；3)阻尼器。该单元每一个节点有一个自由度，单元中的弹簧、阻尼器和间隙控制器可通过用户进行自定义，亦可以从单元中去除。

综合考虑胶合木−钢夹板螺栓连接节点的滞回性能、破坏特性与刚度退化，采用COMBIN40弹簧单元建立连接节点的有限元宏观模型，通过单元的并联可有效模拟连接节点的滞回性能、刚度退化及破坏特性。将5个不同参数设置的COMBIN40弹簧单元进行并联处理，从而得到2节点的连接件有限元宏观模型，如图1所示。

图1 2节点连接件宏观模型

其中模型参数主要根据胶合木−钢夹板螺栓连接节点的力学试验数据及其破坏形态进行定义。有限元宏观模型的COMBIN40单元参数可通过根据试验结果进行设置。

各弹簧单元功能详述如下：

1)单元1由一个弹簧滑动器组成，弹簧刚度为初始结构刚度fund的100倍，其目的是通过调整弹簧刚度与界限滑移力，使螺栓连接在较小荷载下产生初始滑移。

2)单元2由一个弹簧滑动器与一个弹簧并联并与一个阻尼器串联构成，其主要为提供连接件的滞回性能所设。

3) 单元3与单元1相同，由一个弹簧滑动器组成，其主要用来计算连接件屈服点至极限点的刚度退化过程。

4) 单元4由一个弹簧滑动器与一个弹簧并联构成，其主要提供连接件荷载−滑移曲线达到极限点后下降的部分。

5) 单元5为一个弹簧与一个间隙控制器串联构成，单元5是为起到控制作用而设置的，其防止荷载−滑移曲线在单元4的影响下，荷载产生负值。故当连接件的滑动到达间隙值时，单元5将被激活，曲线不再呈现下降趋势。

2 胶合木−钢夹板螺栓连接抗剪性能试验与有限元模型的建立

2.1 抗剪性能试验

根据文献[21]对构件尺寸的要求，设计制作该试验的推出试件(如图2和表1所示)，每个试件仅设置单个螺栓，其中，试件组H20，H40，H60，H480和H100分别代表胶合木厚度为20，40，60，80和10 mm的试件，各试件钢夹板最小端距取30 mm，胶合木最小端距取70 mm。通过原材料松胶合木构件的含水率和密度测定以及抗弯弹性模量以及顺纹抗压强度试验，得到其平均含水率为11.43%，平均气干密度为0.58 g/cm3。平均抗弯弹性模量为11.41 GPa，平均顺纹承压强度为50.64 MPa，试件材性参数均满足我国结构用材要求。各试件均采用8.8级公称直径为8 mm带垫片的普通钢螺栓，螺栓孔开孔直径均为9 mm，钢夹板采用8 mm厚的Q345。

参照文献[22]设计胶合木−钢夹板螺栓连接剪力推出试件的加载方案(如图3所示)。采用500 kN万能试验机进行加载，加载方向沿木材顺纹方向。加载速率为200 N/S。当加载到胶合木和钢夹板之间的滑移值超过2.5 cm或胶合木出现明显开裂破坏即停止加载。

图2 试件构造图

(a) 加载装置示意图；(b) 加载装置照片

表1 试件编号及设计参数汇总表

注：表中1，1，1分别表示钢板的厚度、宽度和长度；2，2，2分别表示胶合木的厚度、宽度和长度；1(1)和2(2)分别表示钢板和胶合木上(下)端距。

2.2 宏观模型的单元选择与参数设置

宏观模型中一维单元采用BEAM188单元[20]进行模拟，模型如图8(a)所示。BEAM188是基于Timoshenko 梁理论[20]进行设置的二节点三维线性梁单元，可应用于线性、大偏转及大应力的非线性分析。结合本课题组开展的胶合木钢夹板连接剪切性能试验[15−18]，得到各胶合木−钢夹板螺栓连接的有限元宏观模型参数，详见表3。

2.3 传统有限元模型

胶合木、钢夹板与螺栓采用SOLID186单元[20]进行模拟，有限元计算模型如图8(b)所示。除螺杆与螺帽采用绑定触外，其余各构件与螺栓间、胶合木与钢夹板间的接触均采用摩擦接触，通过各构件简易摩擦试验以及参考材料接触面摩擦因数的范围，胶合木与钢夹板间摩擦因数取0.35，钢夹板与螺栓之间摩擦因数取0.15[23]。此外，螺帽与垫片间及垫片与钢夹板间均采用粗摩擦接触，即各构件间可法向运动，但不可切向运动。非线性求解采用完全的牛顿−拉普森迭代法，并通过位移控制进行 加载。

2.4 材料本构关系

假定胶合木在线弹性阶段为正交各向异性，但塑性阶段及极限破坏阶段，假定胶合木为各向同性，其在轴向()，径向()和切向()3个方向采用相同的线弹性本构关系。若在塑性阶段同时考虑3个不同方向的屈服应力，很难满足封闭屈服面准则和连续性方程[24]。故本文有限元模型主要考虑试件胶合木的顺纹抗压性能，按照顺纹受压材性试验结果进行模型中胶合木材料强度的设置，且采用理想弹塑性模型。

钢材与木材的塑性阶段采用服从Von Mises屈服准则的双线性等向强化弹塑性本构关系[24]。

(a) 梁单元宏观模型；(b) 传统计算模型

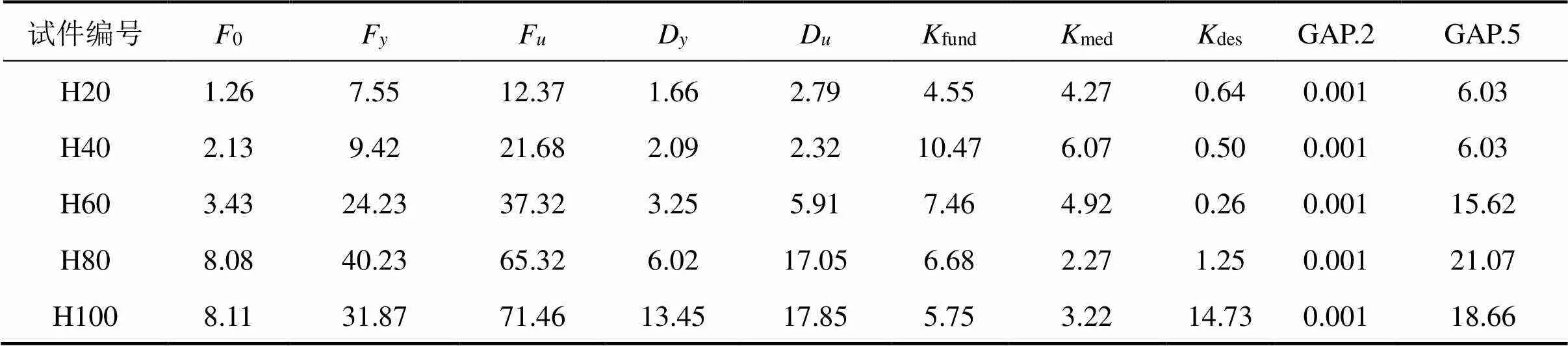
表2 试件宏观模型参数

注：表中0，F，F分别为初始滑移荷载、屈服荷载、极限荷载，kN；D和D分别为屈服荷载、极限荷载对应的位移，mm；fund，med和des分别为结构的初始刚度、塑性刚度、经过极限点的下降刚度、kN/m；Gap.2，Gap.5分别为单元2和单元5的间隙，mm。

3 试验结果与计算结果对比分析

3.1 计算结果对比

结合试件H20，H40，H60，H80和H100(不同厚经比)的试验结果，对比分析试验结果与宏观模型有限元计算结果的荷载−滑移曲线(如图5所示)。

由图5可知，3种方法计算的荷载−滑移曲线基本一致。根据表3抗剪承载力结果可知，传统有限元模型和宏观模型的抗剪承载力最大偏差分别为9.28%和1.16%，表明有限元宏观模型计算更为准确。

为进一步验证有限元模型的准确性，将传统有限元模型计算结果中极限状态的螺栓及垫片的应力云图与试验结果进行对比，如图6所示。

同时，对各试件的抗剪承载力结果进行对比分析，见表3。由图6可知，各螺栓数值模拟结果与试验结果的变形趋势基本一致。由于胶合木采用理想弹塑性模型，这使得螺栓的变形主要集中在钢夹板局部接触位置，螺栓中部与木材接触的弯曲程度相比试验结果较小，但各螺栓的应力分布基本一致，螺栓垫片变形及受力分布与试验结果相一致。

(a) H20、H40试件；(b) H60、H80试件；(c) H100试件

(a) 螺栓结果对比；(b)垫片结果对比

表3 计算结果对比

采用宏观建模方法进行胶合木−钢夹板螺栓连接的计算分析时，设置了5号弹簧单元使得各连接件宏观模型的荷载−滑移曲线的极限状态均出现破坏失效现象，即出现平行于轴的直线段，很好的模拟了连接件的失效状态。

3.2 计算效率对比

为比较各试件宏观模型相比传统有限元模型的计算准确性及计算效率，以相对偏差和计算时间指标进行比较，其中相对偏差为宏观模型计算偏差/传统有限元计算偏差，计算结果见表4。有限元宏观建模方法的计算效率高、收敛性较好，可有效提高具有大量连接的复杂结构非线性分析的计算效率。但是，在应用该模型时还需要一些前提条件：其一，有限元宏观模型的弹簧参数需依据连接件的试验数据来进行设置；其二，有限元宏观模型不能对连接件的应力应变分布进行计算，也不能对结构的破坏特性进行分析，所以，还需进一步加以改进。

表4 计算效率对比

注：表中计算时间表示各试件计算模型的计算时间(时:分:秒)。

4 结论

1) 有限元宏观建模计算方法大大降低了建模计算成本，提高了计算效率，实现了胶合木螺栓连接节点性能的简化有限元计算，为胶合木螺栓连接结构的数值计算带来了便利。

2) 在抗剪承载力方面，胶合木−钢夹板螺栓连接件宏观模型的抗剪承载力最大偏差为1.08%，荷载−滑移曲线与试验结果变化趋势基本一致。有限元宏观模型完全可以弥补传统模型在塑性阶段计算效率较低及收敛性较差等缺点。

3) 有限元宏观模型能够准确地反映木结构螺栓连接节点的剪切性能、滞回性能、滑移特性、刚度退化和失效特性。但是，该模型不能计入连接件各构件由于变形产生的刚度衰减，所以在各构件出现局部分离且变形较大时，还需要进一步研究。

[1] Araújo A S, Oliveira D V, Lourenço P B. Numerical study on the performance of improved masonry-to-timber connections in traditional masonry buildings[J]. Eng Struct, 2014(80): 501−513.

[2] 贺俊筱, 王娟, 杨庆山. 古建筑木结构柱脚节点受力性能试验研究[J]. 建筑结构学报, 2017, 38(8): 141−149. HE Junxiao, WANG Juan, YANG Qingshan. Mechanical property of column footing joint in traditional wooden structure by quasi-static test[J]. Journal of Building Structures, 2017, 38(8): 141−149.

[3] XU B H, Bouchaïr A, Taazount M, et al. Numerical and experimental analyses of multiple-dowel steel-to-timber joints in tension perpendicular to grain[J]. Eng Struct, 2009(31): 2357−2367.

[4] 祝恩淳, 潘景龙, 周晓强, 等. 木结构螺栓连接试验研究及承载力设计值确定[J]. 建筑结构学报, 2016, 37(4): 54−63. ZHU Enchun, PAN Jinglong, ZHOU Xiaoqiang, et al. Experiments of load-carrying capacity of bolted connections in timber structures and determination of design value[J]. Journal of Building Structures, 2016, 37(4): 54−63.

[5] 谢岚. 木−混凝土组合结构螺栓连接件剪切性能研究[D]. 长沙: 中南林业科技大学, 2017. XIE Lan. Shear property of timber-concrete composite structure with nail type connectors[D]. Changsha: Central South University of Forestry and Technology, 2017.

[6] 高永林, 陶忠, 叶燎原, 等. 传统木结构典型榫卯节点基于摩擦机理特性的低周反复加载试验研究[J]. 建筑结构学报, 2015, 36(10): 139−145. GAO Yonglin, TAO Zhong, YE Liaoyuan, et al. Low-cycle reversed loading tests study on typical mortise-tenon joints of traditional timber building based on friction mechanism[J]. Journal of Building Structures, 2015, 36(10): 139−145.

[7] 谢启芳, 郑培君, 向伟, 等.残损古建筑木结构单向直榫榫卯节点抗震性能试验研究[J]. 建筑结构学报, 2014, 35(11): 143−150. XIE Qifang, ZHENG Peijun, XIANG Wei, et al. Experimental study on seismic behavior of damaged straight mortise-tenon joints of ancient timber structures [J]. Journal of Building Structures, 2014, 35(11): 143− 150.

[8] Schneider J, SHEN Y, Stiemer S F, et al. Assessment and comparison of experimental and numerical model studies of cross-laminated timber mechanical connections under cyclic loading[J]. Constr Build Mater, 2015(77): 197− 212.

[9] JIANG L, HU L, CHUI Y H. Finite-element model for wood-based floors with lateral reinforcements[J]. J Struct Eng, 2004(130): 1097−2107.

[10] Mackerle J. Finite element analysis of fastening and joining: A bibliography (1990–2002)[J]. Int J Press Vessels Pip, 2003(80): 253−271.

[11] Mackerle J. Finite element analyses in wood research: A bibliography[J]. Wood Sci Technol, 2005(39): 579−600.

[12] Cachim P B, Franssen J M. Numerical modelling of timber connections under fire loading using a component model[J]. Fire Saf J, 2009(44): 840−853.

[13] Meghlat E M, Oudjene M, Ait-Aider H, et al. A new approach to model nailed and screwed timber joints using the finite element method[J]. Constr Build Mater, 2013(41): 263–269.

[14] Blasetti A S, Hoffman R M, Dinehart D W. Simplified hysteretic finite-element model for timber and viscoelastic polymer connections for the dynamic analysis of shear walls[J]. J Struct Eng, 2008(134): 77–86.

[15] 何朝红. 胶合木−钢夹板螺栓连接力学性能试验研究[D]. 长沙: 中南林业科技大学, 2017. HE Zhaohong. The experimental study on mechanical property of bolted joint with glued timber and steel plate[D]. Changsha: Central South University of Forestry and Technology, 2017.

[16] 陈爱军, 彭容新, 贺国京, 等. 装配式木结构钢夹板螺栓连接抗剪性能[J]. 中国公路学报, 2018, 31(12): 59− 70. CHEN Aijun, PENG Rongxin, HE Guojing, et al. Shear behavior of bolted connections with steel plate in assembled timber structures[J]. China Journal of Highway and Transport, 2018, 31(12): 59−70.

[17] 陈爱军, 唐波, 王解军, 等. 基于销槽承压弹塑性模型的胶合木−钢夹板螺栓连接抗剪性能研究[J]. 公路工程, 2018, 43(6): 11−14, 61. CHEN Aijun, TANG Bo, WANG Jiejun, et al. Study on shear behavior of glued wood-steel splint bolted joint based on elastic-plastic model of pin groove bearing[J]. Highway Engineering, 2018, 43(6): 11−14, 61.

[18] 陈爱军, 牛东, 占雪芳, 等. 钢夹板−螺栓连接胶合木抗剪性能试验研究[J]. 中南林业科技大学学报, 2018, 38(9): 115−119. CHEN Aijun, NIU Dong, ZHAN Xuefang, et al. Experimental study on connection performance of glued wood-steel clamp bolted connection[J]. Journal of Central South University of Forestry & Technology, 2018, 38(9): 115−119.

[19] Pablo A, Lacourt, Francisco J, et al. Finite element modelling of hysteresis, degradation and failure of dowel type timber joints[J]. Eng Struct, 2016(123): 89–96.

[20] ANSYS Inc. ANSYS@workbench release 12.0, help system, mechanical user’s guide[M]. United States of America: Washington, 2009.

[21] GB 50005—2003, 木结构设计规范[S]. GB 50005—2003, Code for design of timber structures[S].

[22] GB/T 50329—2012, 木结构试验方法标准[S]. GB/T50329-2012, Standard for test methods of timber structures[S].

[23] ISO 16670, Timber structures-joints made with mechanical fasteners-quasi-static reversed-cyclic test method[S].

[24] 王明谦, 宋晓滨, 顾祥林, 等. 胶合木梁柱螺栓−钢填板节点转动性能研究[J]. 建筑结构学报, 2014, 35(9): 141−150. WANG Mingqian, SONG Xiaobin, GU Xianglin, et al. Study on rotational behavior of bolted glulam beam-to- column connections with slotted-in steel plates[J]. Journal of Building Structures, 2014, 35(9): 141−150.

Numerical simulation of bolted connections with steel plate in glued wood based on the macroscopic modeling method

CHEN Aijun, HE Guojing, WANG Zhifeng, WANG Jiejun

(School of Civil Engineering, Central South University of Forestry and Technology, Changsha 410004, China)

In order to solve the problems of low efficiency and poor convergence of the 3D finite element model of bolted connections with steel plate in glued wood, a finite element macro modeling method was adopted. This method was used to simulate the bolted connections with steel plate in glued wood through the combination of nonlinear elements, and simplified the finite element calculation of the node performance of bolted connections with steel plate in glued wood. At the same time, the macroscopic model and the traditional 3D finite element model of each connections were established based on the test of the shear behavior of the connection joints of glued laminated timber connections with steel plate. The computational efficiency and precision of the finite element macroscopic model were verified by comparing the results of the macroscopic model with the traditional finite element model and the experimental results of mechanical properties. The traditional finite element model, macro model and mechanical test results of bolted connections with steel plate in glued wood are consistent with each other. The macro model can correctly reflect the shear properties, slip characteristics, hysteretic behaviors,stiffness degradation and failure characteristics of the bolted connections with steel plate in glued wood. Compared with the traditional 3D finite element method, the calculation cost of the macro model is relatively low, and the convergence is good. The finite element macro modeling method can effectively improve the computational efficiency of nonlinear analysis of complex structures with large number of connections.

macroscopic modeling method; bolted glued laminated timber connections with steel plate; macroscopic model; numerical simulation; shear behavior

TU311

A

1672 − 7029(2020)05 − 1244 − 08

10.19713/j.cnki.43−1423/u.T20190679

2019−07−30

国家自然科学基金资助项目(51578554)；国家林业公益性行业科研专项经费资助项目(201304504)；现代木结构工程材制造及应用技术湖南省工程实验室开放基金资助项目(HELFMTS1705)；湖南省教育厅科研基金资助项目(19A526，16C1665)

王智丰(1984−)，男，湖南岳阳人，讲师，博士，从事木结构桥梁设计与振动研究；E−mail：310682339@qq.com

(编辑 蒋学东)