边条翼夹板结构强度设计

王 珊,杨梦琳,康洪海,王 栋

(北京航天微系统研究所,北京 100094)

边条翼夹板结构强度设计

王 珊,杨梦琳,康洪海,王 栋

(北京航天微系统研究所,北京 100094)

利用解析与有限元方法分别对3种结构形式的导弹边条翼夹板进行了强度对比分析。分析得出了这3种形式夹板的受力特点以及承载能力的强弱。在此基础上,进一步采用有限元方法对不同形式夹板两两组合运用时的力学性能进行了数值仿真对比,给出了各组夹板的应力分布规律,推荐了较优的组合方案。最后对夹板厚度进行了优化设计。文中研究可为夹板结构设计提供参考依据。

夹板;强度;有限元;应力

0 引言

弹翼是有翼导弹的主要升力部件,其空气动力为导弹提供机动飞行时的法向力[1]。边条翼夹板是连接边条翼与弹身的结构件。在边条翼所承受的气动力作用下,夹板主要承受剪力与弯矩载荷[2],其中弯矩对夹板根部应力分布影响尤为显著。合理的夹板设计可有效降低局部应力集中,提高材料性能利用率及结构安全性。

近年来,在导弹弹翼强度分析方面已经有了一些研究[3-4],然而讨论边条翼夹板强度的工作还比较少。文中利用梁纯弯曲理论公式和三维实体有限元方法分别对3种结构形式的边条翼夹板进行了解析和数值的强度分析,通过对比分析结果,得出了较优的结构形式。在实际应用中,不同形式的夹板经常两两组合使用。文中针对某型号在结构设计中所考虑的夹板组合形式进行了有限元强度分析,得出了几种组合形式下夹板的应力分布,给出了较优的组合形式,并对边条翼夹板厚度进行了优化,以便为边条翼夹板结构与强度设计提供参考依据。

1 单个夹板力学性能分析

某型号导弹边条翼夹板结构设计中先后考虑了3种设计方案,3种方案均采用双片夹板的结构形式,两片夹板分别贴紧边条翼根部两侧。3种方案在承力部位和尺寸上所有区别,可分别描述为:(a)第一类:承力部位为固定在弹身上的单侧夹板,另一侧夹板不与弹身相连接,仅起到配合固定夹板夹紧弹翼的作用,此形式夹板在文中中称为单片单倍厚度;(b)第二类:在上一种形式的基础上,将固定一侧承力夹板厚度加倍,文中称为单片双倍厚度;(c)第三类:两侧夹板均固定于弹身,两侧夹板同时承力,每片夹板厚度与第一种形式相同,文中称为双片单倍厚度。这3种夹板的受弯截面如图1所示,图中各几何量的值见表1。

图1 夹板承弯截面

几何量/mmbhl取值68.447.5

在边条翼气动载荷作用下,夹板根部承受的弯矩最大,该截面最大应力发生于距离中性轴最远处。弯曲截面最大正应力σmax公式为[5]:

σmax=Mmax/W

(1)

式中:Mmax代表最大截面弯矩;W称为抗弯截面系数,且:

W=Iz/ymax

(2)

式中:Iz、ymax分别代表截面对中性轴的惯性矩和距中性轴最大距离。抗弯截面系数W与截面的几何形状有关。对于如图1(a)所示截面是高为h、宽为b的矩形,截面对中性轴的惯性矩为:

Iz=bh3/12

(3)

则抗弯截面系数为:

W1=Iz/(h/2)=bh3/12/(h/2)=bh2/6

(4)

如图1(b)所示截面为高为2h、宽为b的矩形,则:

(5)

对于如图1(c)所示由两个高为h、宽为b的矩形组成的复杂截面,两矩形之间距离为l,则该复杂截面对截面中性轴的惯性矩为:

Iz=b(2h+l)3/12-bl3/12

(6)

则抗弯截面系数为:

(7)

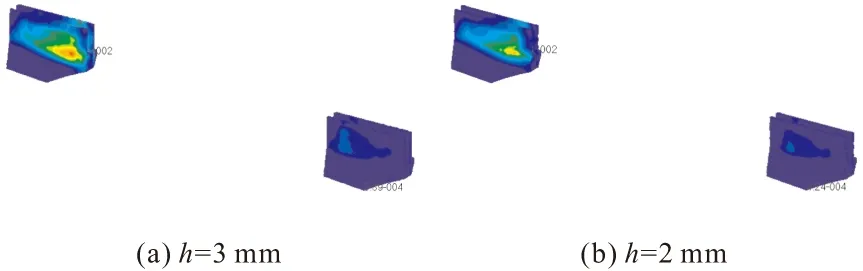
由式(4)、式(5)、式(7)的表达式可以看出,3种类型夹板的抗弯截面系数有关系式W1

若单个夹板承受的气动力为F,气动压心距离夹板根部距离为L,夹板根部截面弯矩可表示为:

Mmax=FL

(8)

求出了这3种截面的抗弯截面系数W1、W2、W3,对于任意截面弯矩Mmax都可以利用式(2)求出最大弯曲正应力。除此之外,气动力的作用还将使夹板截面产生剪应力:

τ=F/A=F/(bh)

(9)

式中A=bh代表截面面积。由最大正应力和剪应力可得出截面最大第四强度理论等效应力:

(10)

作为与解析方法的对比,运用有限元方法对3种夹板进行数值仿真。夹板上通常存在通孔或螺纹孔以实现与弹翼以及对侧夹板的连接。但由于该孔距离夹板根部较远,且不作为重点考察部位,在本计算中将其影响忽略不计。利用软件Patran建立有限元模型,采用四面体单元对夹板进行网格划分。约束夹板与弹体连接面三个方向平动自由度。通过建立辅助工装模型在距离夹板根部66 mm处施加800 N的集中力以模拟气动载荷,气动载荷方向垂直于夹板板面。夹板材料为45#钢,机械性能为HRC25～26,弹性模量200 GPa,泊松比0.3,屈服极限575 MPa,强度极限825 MPa。3种夹板有限元模型及应力云图如图2所示。解析方法与有限元法计算所得最大应力的对比见表2。

图2 3种夹板有限元模型及应力云图

夹板类型最大Von-Mises应力/MPa解析法有限元法(a)单片单倍厚度290306(b)单片双倍厚度7274.6(c)双片单倍厚度2233

从图2应力云图可以看出,在气动力作用下3种夹板最大应力都发生在距离载荷最远的根部区域。由表2所列3种类型夹板最大应力计算结果对比可以看出:第一类夹板应力最大,承载力最低;第二类夹板的横截面积是第一类夹板的2倍,抗弯截面系数是第一类夹板的4倍,最大应力约为第一类夹板的四分之一,承载力明显优于第一类夹板;第三类夹板的横截面积与第二类相同,由于两片承力夹板分开一定的距离使得第三类夹板的抗弯截面系数增大至约为第二类夹板的3倍,最大应力约为第二类夹板的三分之一,第一类夹板的十至十三分之一,承载力显著优于前两类夹板。从求解方法来看,解析法计算的是理论平均值,在距截面中性轴距离相等的位置应力值相同。有限元法计算出的是数值解,得到应力在几何体上的整体分布规律,在距截面中性轴距离相同的位置所得的应力有可能不同。有限元解在某些部位大于解析解,某些部位小于解析解,在解析解周围分布。由此可见有限元法计算的最大应力略较解析法偏大是合理的。

第二类夹板基于第一类夹板的结构设计,单纯考虑到通过改变弯曲截面几何尺寸,增大厚度,从而提高夹板强度。由于前两类夹板除了固定于弹身上的承力单片外,还有另外一片悬空于弹体不承受气动力引起的弯矩与剪力,只起到与固定片配合夹紧边条翼的作用,因此在夹板的整体耗材上第二类夹板是第一类夹板的1.5倍。第三类夹板的耗材量与第一类夹板相同,其两侧单片均固定于弹身,不但起到固定弹翼的作用,并且共同承受气动载荷。通过对比三类夹板的耗材量与承载能力可以看出:第二类夹板比第一类夹板耗材量增加50%,力学性能提升至第一类的约4倍;第三类夹板的耗材量相比第一类并无增加,力学性能却提升至第一类的约10～13倍。显而易见,从结构优化的角度上看,第三类夹板的力学性能是最优的。在结构设计中,恰当使用第三类夹板可节省耗材,并使结构承载力大幅提高,而第二类夹板则相对来说不推荐使用。

2 组合夹板强度分析

上节讨论了单个夹板的力学性能,而在实际设计中经常是两组夹板配合使用。本节将就两两组合夹板的力学性能展开讨论,组合类型包括:(a)第一类-第一类;(b)第三类-第一类;(c)第三类-第三类。其中前后两种类型分别代表前夹板和后夹板的夹板类型。

建立边条翼与夹板有限元模型,采用四面体单元对边条翼与夹板进行一体的网格划分,其中边条翼仅起到加载工装作用。约束夹板与弹体连接面三个方向平动自由度。将边条翼展长1/2,弦长前1/3处作为气动压心施加3 000 N气动力,气动力方向垂直于边条翼翼面。有限元模型示意如图3所示,经分析计算得到3组夹板应力云图如图4所示,最大等效应力见表3。

图3 边条翼与夹板有限元模型

图4 3组夹板Von-Mises应力云图

组合夹板类型最大Von-Mises应力/MPa前夹板后夹板(a)第一类-第一类688199(b)第三类-第一类11480(c)第三类-第三类11121

由于气动力作用点位置靠近前夹板,因此前夹板为主要承力部件。图4应力云图和表3数据结果表明,3种组合夹板的最大应力均发生在前夹板根部区域。(a)组夹板应力水平最高,前夹板最大应力达到688 MPa,超过了45#钢的屈服极限,强度不满足要求,该设计不可采用。(b)组夹板在(a)组夹板基础上将前夹板更换为第三类夹板,前后夹板整体应力水平显著降低,前夹板最大应力仅为114 MPa,约为(a)组前夹板最大应力的16.6%,后夹板最大应力为(a)组后夹板的40.2%。由此可见,合力采用第三类夹板可有效降低整体应力水平,提高结构承载力。(c)组夹板在(b)组夹板基础上将后夹板也更换为第三类夹板,由于起主要承载作用的是前夹板,后夹板承载作用较小,因此更换后夹板后对前夹板最大应力并无显著改善,与(b)组前夹板最大应力较为接近,后夹板最大应力约为(b)组后夹板的四分之一。(b)组夹板与(c)组夹板在3 000 N气动载荷作用下的最大应力显著低于(a)组夹板,低于45#钢的屈服极限,满足强度要求。

3 静力试验

对安装(b)组夹板的边条翼进行静力试验。夹板固定于静力试验工装,在边条翼展长1/2,弦长前1/3处打孔穿拉杆用以施加垂直于翼面的拉力,以模拟气动压心施加3 000 N气动力如图5所示,边条翼仅作为加载工装使用。先后进行两次加载,分别加载至3 000 N与7 000 N并保持10 s后卸载。拆卸边条翼,观察夹板,夹板未发生明显塑性变形及破坏。由此可知试验载荷未使夹板最大应力达到45#钢屈服极限,此结论与数值计算结果相符。

图5 静力试验示意图

4 优化设计

从数值分析与静力试验结果可知,(b)、(c)两组夹板满足强度设计要求,是较为理想的夹板组合形式,并有一定安全余量可进一步进行结构优化。分别对两组减薄厚度h的(b)、(c)组夹板进行强度分析,分析得到夹板应力云图如图6、7所示,最大应力见表4。

图6 (b)组夹板优化设计Von-Mises应力云图

图7 (c)组夹板优化设计Von-Mises应力云图

(b)组夹板分析结果表明,当夹板厚度从4 mm减薄至3 mm,前夹板最大应力从114 MPa增大至127 MPa,后夹板最大应力从80 MPa增大至100 MPa,前后夹板最大应力增幅约为25%。当夹板厚度继续减至2 mm,夹板应力增大较为显著,前后夹板最大应力分别增大至280 MPa和172 MPa,前后夹板最大应力增幅分别为145%和115%,应力值低于45#钢屈服极限,夹板强度满足要求,且有一定的安全余量。

表4 组夹板优化设计最大Von-Mises应力

(c)组夹板与(b)组夹板前夹板最大应力较为接近,(c)组前夹板应力略低于(b)组夹板前夹板。(c)组后夹板最大应力约为(b)组后夹板的四分之一。减薄后的(c)组夹板最大应力值低于45#钢屈服极限,强度满足要求,且有一定的安全余量。

除强度必须满足要求外,实际设计中还应考虑夹板与边条翼的整体刚度对气动外形的影响,由于篇幅的限制,文中对此不展开讨论。

5 结论

夹板是导弹边条翼与弹体间常用的连接结构件,主要承受边条翼传递的气动载荷。文中采用解析法和有限元数值方法对3种类型夹板的承载能力进行了理论计算和分析对比,结果表明第三类夹板承载能力最强,且耗材最少质量最小,符合结构优化设计的思想。进而对实际设计中常见的三种两两组合夹板的力学性能进行了考核,结果表明前后夹板都使用第三类夹板时应力水平最低,前后夹板分别使用第三类和第一类夹板的应力水平次之,前后夹板都使用第一类夹板的承载力最弱。基于有限元结果与静力试验,对夹板结构进行了优化设计。文中研究可为边条翼夹板结构与强度设计提供参考依据。

[1] 余旭东, 葛金玉, 段德高, 等. 导弹现代结构设计 [M]. 北京: 国防工业出版社, 2007: 184-185.

[2] 成楚之. 火箭与导弹的静动力载荷设计 [M]. 北京: 宇航出版社, 1994: 112-115.

[3] 宋彦国, 杨炳渊. 应用结构动力学模型进行弹翼静强度计算 [J]. 上海航天, 2000(2): 30-33.

[4] 杜厦, 昂海松. 一种改进折叠弹翼结构设计与气动分析 [J]. 航空兵器, 2009(3): 7-9.

[5] 刘鸿文. 材料力学 [M]. 4版. 北京: 高等教育出版社, 2004: 138-143.

The Design of Strake Wing Structural Strength

WANG Shan,YANG Menglin,KANG Honghai,WANG Dong

(Beijing Aerospace Microsystems Institute, Beijing 100094, China)

By using analytical and finite element methods, three structural forms of the missile strake wing splint were analysed and contrasted. The stress characteristics and bearing capacity of three kinds of splint was obtained. Basing on this, finite element method was used to simulate and compare the mechanical performance of different types of splint when used in combination, then the stress distribution law of each group of splints was obtained. And a better combination scheme was recommended. At last, optimal design of splint thickness was carried out. This study provided reference for splint structural design.

splint; strength; finite element; stress

2016-03-19

王珊(1981-),女,辽宁大连人,高级工程师,博士,研究方向:飞行器环境载荷与结构强度设计。

TJ760.2

A