有翼导弹动态气动特性数值研究

张瑞民,时晓天

(中国航天空气动力技术研究院,北京 100074)

有翼导弹动态气动特性数值研究

张瑞民,时晓天

(中国航天空气动力技术研究院,北京 100074)

为准确预测飞行器的机动特性,故开展其动态气动特性研究。应用非结构动网格技术建立了可模拟飞行器作周期性俯仰运动的强迫振荡法。选取NACA 0012翼型为研究对象对该方法进行验证,进而计算了有翼导弹Finner在各马赫数下的静、动导数,并分析了Finner导弹在不同减缩频率下的动态气动迟滞特性。结果表明,文中方法能够有效模拟有翼导弹在不同马赫数下的动态气动特性,结果正确可靠,具有较高的工程应用价值。

有翼导弹;动态特性;气动特性;动网格;俯仰振荡

0 引言

对于新一代高性能战斗机和导弹而言,必须要具备大攻角机动的飞行能力。因此,准确的预测飞行器的动态性能显得尤为重要。

1990年之前,动导数预测以风洞实验和工程估算为主。然而,工程估算仅适用于简单外形,且无法满足不同工况下的动导数预测;风洞实验对模拟技术、测量手段要求较高,且实验费用昂贵,更不可避免地存在着系统机构阻尼、支架干扰、洞壁干扰及重心位置干扰等因素,大大影响了实验结果的准确性。数值模拟方法不存在上述问题,但也面临着一系列的重大挑战,尤其是非定常模拟的效率问题和精度问题[1]。

随着计算机性能的提高以及非定常流场数值模拟技术的飞速发展,应用数值方法来预测飞行器的动态气动特性日益成熟。文献[2-7]采用当地活塞理论方法或者改进的工程计算方法研究了飞行器作周期性振荡的动态气动特性;文献[8]采用谐波平衡法预测了飞行器的周期性非定常流动特性,计算效率很高;文献[9-17]采用数值模拟技术研究了各种飞行器作俯仰振荡运动的动态特性;文献[18-19]采用CFD技术计算了飞行器的动导数,还分析了减缩频率对动态特性的影响。

借鉴前人的研究成果,文中应用非结构化动网格技术模拟了Finner导弹绕固定轴旋转作俯仰振荡运动的整个过程,计算了该导弹在不同马赫数下的静、动导数,并对该导弹在不同减缩频率的动态气动特性进行了分析。

1 数值方法

1.1 数值算法与湍流模型

文中采用Transition SST湍流模型进行计算,该模型是在SSTk-w的基础上增加了有关间歇度γ和转捩发生准则的两种输运方程,其捕捉流场细节精度更高。

1.2 控制方程与离散方法

流场计算采用Pressure-Velocity Coupling算法中的Coupled方法来求解三维非定常可压粘流时均N-S方程。空间离散采用格心格式的有限体积法,时间离散采用隐式离散方法进行双时间推进。

1.3 动网格技术

动网格技术可以用来模拟流场边界随时间变化的问题。网格的更新过程是根据每次迭代中边界的变化情况自动完成。在任一控制单元中,广义标量Φ的积分守恒方程为:

(1)

式中:ρ为流体密度;u为速度流量;ug为移动网格的网格速度;Γ为扩散系数;SΦ为源项;∂V为控制单元V的边界;A为控制单元的面积。

1.4 网格划分与边界条件

文中采用商用软件ICEM对Finner导弹模型进行了非结构化网格划分,远场边界到翼型表面的距离设为弦长的20倍,翼型表面设定为无滑移壁面边界,且对翼型附近网格进行了局部加密。

1.5 动导数辨识

对于单自由度强迫俯仰振荡,其运动形式如下:

α=α0+αmsin(ωt)

(2)

式中:α0为初始攻角;αm为振荡幅值;ω为振荡圆频率。

假设飞行器为对称直线飞行,且振幅很小,在计算中仅考虑一阶动导数,忽略高阶动导数,那么,俯仰力矩在初始攻角处作泰勒展开有:

(3)

飞行器作低频小幅振荡的运动方程简化如下:

(4)

将式(4)代入式(3),合并同类项,可得:

(5)

式(5)沿迟滞环线积分,可得:

(6)

由此可得:

(7)

通过无因次化,可得:

(8)

式中：k=ωlref/2V为减缩频率;lref为模型参考长度;v为来流速度。

2 方法验证

采用国际标准算例AGARD CT5[20]来验证文中方法。NACA 0012翼型作俯仰振荡运动,其轴心位于翼型前缘1/4弦长处,计算状态如表1。

表1 计算条件

图1和图2分别给出了升力系数和俯仰力矩系数随迎角变化的迟滞曲线。从图中可以看出,文中结果与实验数据及参考值吻合较好,表明文中数值方法正确可靠。

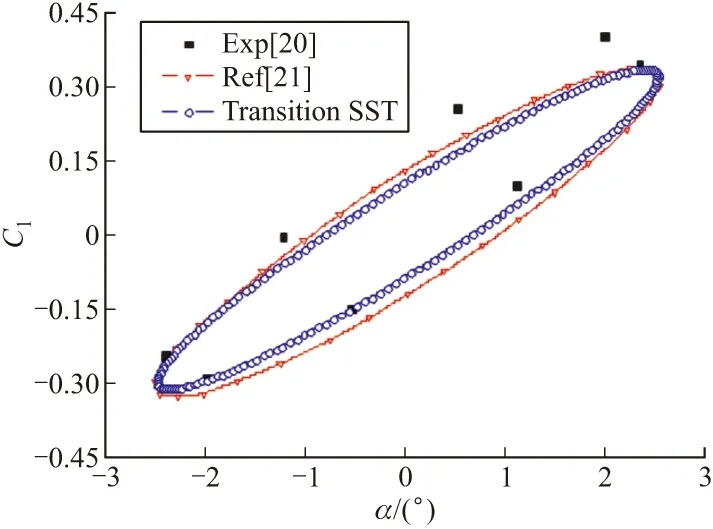
图1 升力系数随迎角的变化

图2 俯仰力矩系数随迎角的变化

3 算例与分析

3.1 模型与网格

算例选取国际动导数标模Finner导弹[22],几何外形见图3,模型网格划分见图4。

图3 导弹外形示意图

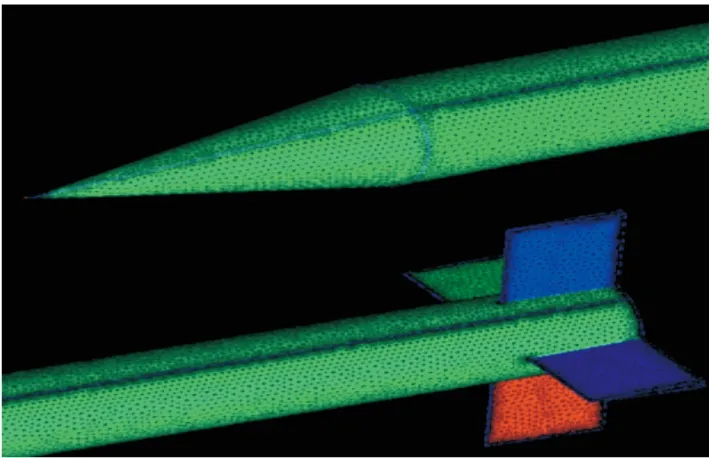
图4 Finner模型网格

3.2 静导数计算

图5和图6分别给出了0°攻角、0.5～4.5Ma下的Finner导弹的法向力和俯仰力矩静导数系数,并与文献[22-23]中的实验数据和计算结果进行了比较。从图中可以看出,与参考值相比,文中结果更接近于实验结果。图7给出了Finner导弹在0°攻角下、Ma=0.9时x-z对称面的马赫数云图。从图中可以清楚地看到弹体头部和尾翼后侧的激波形成以及弹体尾端的低速流动区域。

图5 Finner导弹在0°攻角时、不同马赫数下的法向力静导数

图6 Finner导弹在0°攻角时、不同马赫数下的俯仰力矩静导数

图7 Finner导弹在0°攻角时、0.9Ma x-z对称面的马赫数云图

3.3 动导数计算

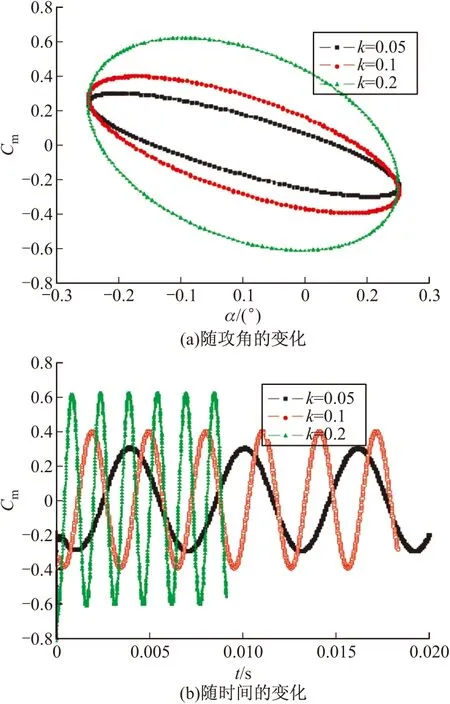
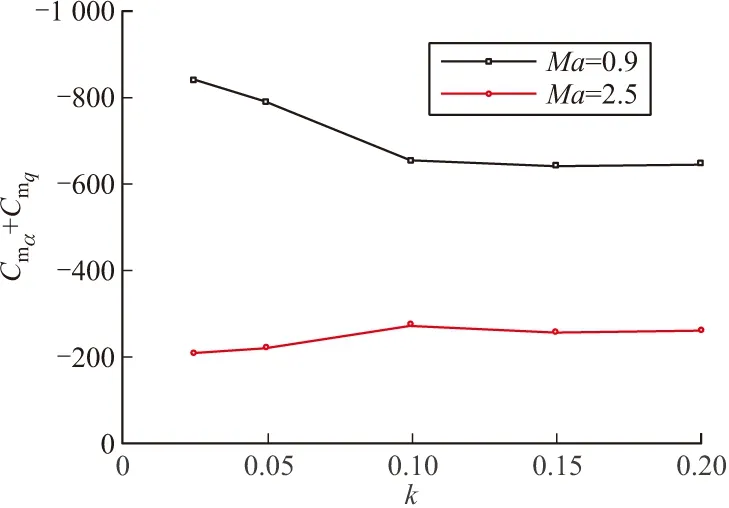
Finner导弹动导数的计算条件见表2。图8给出了0°攻角、0.5～4.5Ma下Finner导弹的俯仰力矩动导数,并与文献[21-22]中的实验数据和计算结果进行了比较。可以看出,除0.9

表2 计算条件

图8 Finner导弹在0°攻角、不同马赫数的俯仰组合动导数

3.4 减缩频率影响

图9给出了马赫数为0.9时不同减缩频率下Finner导弹的俯仰力矩系数随着攻角和时间的变化。可以看出,俯仰力矩系数随攻角变化的迟滞曲线图均以(α,Cm)=(0,0)为圆心,且随着减缩频率的增加,离心率不断减小;俯仰力矩系数随着时间变化的曲线图呈正弦波,且随着减缩频率的增加,正弦波的频率和幅值均增大。图10给出不同马赫数下俯仰阻尼动导数系数随减缩频率的变化。从图中可以看出,当减缩频率在0.025到0.1之间时,随着减缩频率的增加,俯仰阻尼动导数系数变化较大;当减缩频率大于0.1时,俯仰阻尼动导数系数基本不变。

图9 0.9 Ma下不同减缩频率对俯仰力矩系数的影响

图10 不同马赫数下减缩频率对俯仰阻尼动导数系数的影响

4 结论

文中应用计算流体力学软件Fluent中的动网格技术和UDF方法模拟了Finner导弹作俯仰振荡运动的动态气动特性,并与参考文献中的实验数据和计算结果进行了比较,得出的主要结论如下:

1)文中关于Finner导弹在亚跨超高速不同马赫数下静、动导数的预测结果很好,说明文中数值方法正确可靠。

2)俯仰力矩系数随着攻角变化的迟滞曲线图以(α,Cm)=(0,0)为圆心,且随着减缩频率的增加,离心率不断减小;俯仰力矩系数随着时间变化的曲线图呈正弦波,且随着减缩频率的增加,正弦波的频率和幅值均增大。

3)当减缩频率在0.025～0.1之间,随着减缩频率的增加,俯仰阻尼动导数系数变化较大;当减缩频率大于0.1时,俯仰阻尼动导数系数基本不变。

[1] 李周复. 风洞特种实验技术 [M]. 北京: 航空工业出版社, 2010: 240-242.

[2] TONG B G, HUI W H. Unsteady embedded Newton-Busemann flow theory [J]. Journal of Spacecraft and Rockets, 1986, 23(2): 129-135.

[3] EAST R A, HUTT G R. Comparison of predictions and experimental data for hypersonic pitching motion stability [J]. Journal of Spacecraft and Rockets, 1988, 25(3): 225-233.

[4] 张伟伟, 史爱明, 王刚, 等. 结合定常CFD技术的当地流活塞理论 [J]. 西北工业大学学报, 2004, 22(5): 545-549.

[5] ZHANG Weiwei, YE Zhengyin, ZHANG Chenan, et al. Supersonic flutter analysis based on local piston theory [J]. AIAA Journal, 2009, 47(10): 2321-2328.

[6] 卢学成, 叶正寅, 张伟伟. 超音速、高超音速飞行器动导数的高效计算方法 [J]. 航空计算技术, 2008, 38(3): 28-31.

[7] 刘溢浪, 张伟伟, 田八林, 等. 一种超音速高超音速动导数的高效计算方法 [J]. 西北工业大学学报, 2013, 31(5): 824-828.

[8] 陈琦, 陈坚强, 袁先旭, 等. 谐波平衡阀在动导数快速预测中的应用研究 [J]. 力学学报, 2014, 46(2): 183-190.

[9] DUBUC L, CANTARITI F, WOODGATE M, et al. Solution of the unsteady Euler equations using an implicit dual-time method [J]. AIAA Journal, 1998, 36(8): 1417-1424.

[10] PARK S H, KIM Y, KWON J H. Prediction of dynamic damping coefficients using unsteady dual-time stepping method: AIAA 2002-0715 [R]. 2002: 1-9.

[11] OKTAY E, AKAY H U. CFD predictions of dynamic derivatives for missiles: AIAA 2002-0276 [R]. 2002: 1-10.

[12] GREEN L L, SPENCE A M, MURPHY P C. Computational methods for dynamic stability and control derivatives: AIAA 2004-0015 [R]. 2004: 1-17.

[13] MURMAN S M. Reduced-frequency approach for calculating dynamic derivatives [J]. 2007, 45(6): 1161-1168.

[14] 袁先旭, 张涵信, 谢昱飞. 基于CFD方法的俯仰静、动导数数值计算 [J]. 空气动力学学报, 2005, 23(4): 458-463.

[15] 史爱明, 杨永年, 叶正寅. 结合CFD技术的跨音速动导数计算方法研究 [J]. 西北工业大学学报, 2008, 26(1): 11-14.

[16] 范晶晶, 阎超, 李跃军. 飞行器大迎角下俯仰静、动导数的数值计算 [J]. 航空学报, 2009, 30(10): 1846-1850.

[17] 孙智伟, 程泽荫, 白俊强, 等. 基于准定常的飞行器动导数的高效计算方法 [J]. 飞行力学, 2010, 28(2): 28-30.

[18] 孙涛, 高正红, 黄江涛. 基于CFD的动导数计算与减缩频率影响分析 [J]. 飞行力学, 2011, 29(4): 15-18.

[19] BATINA J T. Unsteady Euler airfoil solutions using unstructured dynamic meshes [J]. AIAA Journal, 1990, 28(8): 1381-1388.

[20] LANDON R H. NACA 0012 oscillatory and transient pitching: ADP 010 707 [R]. 2000.

[21] LI J, HUANG S Z, JIANG S J, et al. Unsteady viscous flow simulations by a fully implicit method with deforming grid: AIAA 2005-1221 [R]. 2005: 1-10.

[22] WEST K O. Comparison of free-flight spark range and wind tunnel test data for a generic missile configuration at mach numbers from 0.6 to 2.5: AFATL-TR-81-87 [R]. Florida:Air Force Armament Laboratory, 1981.

[23] SAHU J. Numerical computations of dynamic derivatives of a finned projectile using a time-accurate CFD method: AIAA 2007-6581 [R]. 2007: 1-13.

Research on Numerical Virtual Flight of Spinning Projectile

ZHANG Ruimin,SHI Xiaotian

(China Academy of Aerospace Aerodynamics, Beijing 100074, China)

In order to accurately predict the maneuvering characteristics of the aircraft, dynamic aerodynamics was then studied. Dynamic unstructured mesh technology in computational fluid dynamics was used to build forced oscillation method which could simulate the periodic pitching motion of the aircraft. The NACA 0012 airfoil was selected as the research object to validate the method. The static and dynamic derivatives winged missile Finner under different Mach numbers were computed and the dynamic aerodynamic hysteresis characteristics under different reduced frequencies were analyzed. The results showed that the method in the paper could effectively and correctly simulate the dynamic aerodynamic characteristics of winged missile under different Mach numbers and it could find wide application in engineering.

winged missile; dynamic characteristics; aerodynamic characteristics; dynamic mesh; pitching oscillation

2016-03-03

张瑞民(1980-),男,山西运城人,高级工程师,博士,研究方向:空气动力学、飞行动力学和多相流研究。

V211.3

A