多约束集群目标下武器-目标分配问题

张 凯，周德云，杨 振，潘 潜

（西北工业大学电子信息学院，西安710072）

（*通信作者电子邮箱zhangkainwpu@mail.nwpu.edu.cn）

0 引言

随着军事技术和作战概念的发展，集群智能体成为未来战场的作战主体已是必然趋势。在近年美国国防高级研究局（Defense Advanced Research Projects Agency，DARPA）推出的小精灵项目、海军/空军低成本无人机集群技术中，其作战单位均具有低探测性、低成本、可回收、零人员伤亡等优点，并可协同完成多方位、多批次、高密度的饱和攻击。2016 年美军发布的《小型无人机系统路线图2016—2036》指出小型无人机系统及其集群对情报、侦察与监视领域具有“填补战术与战略之间空白”的重要意义，并预计在2025 年以后，无人机将具有集群战场认知能力，实现完全自组织作战［1］。

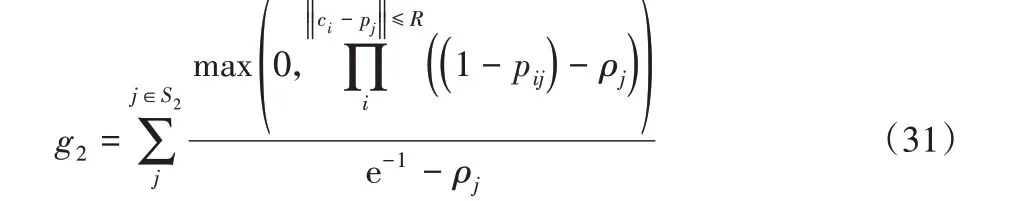
当目标毁伤概率向量满足目标毁伤门限向量ρ时，g2(x)为0；反之，g1(x)与毁伤门限的偏离程度成正比。

武器-目标偏好指派约束的约束违反值设计为:

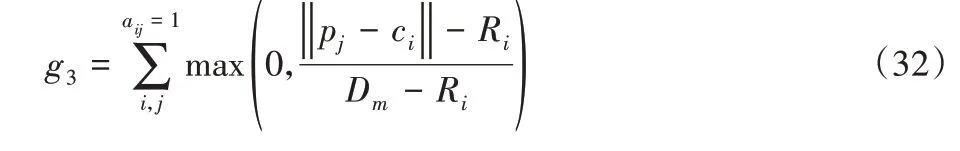
当目标处于偏好武器的杀伤范围内时，g3(x)为0；反之g3(x)与目标-偏好武器的距离成正比。

2.4 性能度量

在对多目标优化算法的性能度量中，一般评估所得Pareto 前沿面的收敛性和分布性。前者评价解得Pareto 解集与真实Pareto 集合的趋紧程度，如Convergence 指标［22］；分布性评价Pareto集合在目标空间中的均匀性、多样性，如Spacing指标［23］。在CMWTA 问题中，由于解集在目标空间中呈现分层递减的特定非均匀分布，因此无需分布性反映Pareto 前沿面的优劣。而一般收敛性指标需要理论最优解，而通常无法得到CMWTA 问题的理论最优解，因此本文在比较不同算法收敛性的优劣时，设计针对CMWTA模型的Convergence变式:令P={p1，p2，…，p||P}为不同算法对同一CMWTA问题求解的历史解集形成的近似Pareto 最优解集合，A={a1，a2，…，a||A}为单次求解得到的近似Pareto 最优解集合，通过下式计算该解集距离P的近似归一化距离:

除了设计Convergence变式给出CMWTA算法收敛性的定量评价外，另采用Coverage指标［24］进行各算法的定性评价:

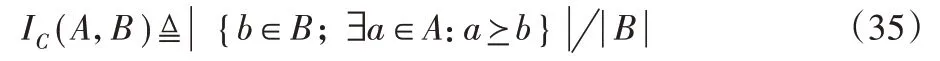
其中:解集A、B分别为同一算例用不同算法解得的Pareto 集合，通常IC(A，B)≠IC(B，A)，且IC(A，B)＞IC(B，A)时，表明解集A优于解集B。

3 仿真与分析

算例1 为便于研究，引入以下作战想定:假设在二维场景中并略去相应单位，战场环境大小为20×20，其中集群威胁目标个体数量为20，存在2 个友方/中立目标，阿拉伯数字1～20 代表威胁目标，圆点代表友方/中立目标，目标6 和目标13后的不等式表示其生存概率门限值分别为0.2和0.1，目标14后的罗马数字Ⅲ表示优先将武器3 分配给该目标，如图2 所示。己方可使用的武器数量为30，武器有效杀伤半径为［2.1:0.1:5］。相关参数见表1。

图2 算例1作战场景态势图Fig. 2 Situation diagram of fighting scenario of example one

表1 算例1装订数据Tab. 1 Numerical values of example one

分别采用多目标进化算法中具有代表性的NSGA-Ⅱ（Non-dominated Sorting Genetic Algorithm Ⅱ）［25］、SPEA2（Strength Pareto Evolutionary Algorithm Ⅱ）［26］和MOEA/D（Multi-Objective Evolutionary Algorithm based on Decomposition）［27］框架对上述模型进行求解。为了不影响以上三种算法求解CMWTA 问题的对比分析，此算例中的三种算法均采用了修复策略。关于修复算法对算法的影响在算例2中进行仿真分析。本算例中相关算法参数如下:

NSGA-Ⅱ:种群规模N=1 200，交配池规模MP=600，终止代数tmax= 100，交叉概率Pc= 0.8，变异概率Pm= 0.2，交叉分布指数ηc= 1，变异分布指数ηm= 1。

SPEA2:种群数量N= 1000，存档集规模M= 200，交配池规模MP= 100，终止种群代数tmax= 100，邻近值k= 35，交叉概率Pc= 0.8，变异概率Pm= 0.2，交叉分布指数ηc= 1，变异分布指数ηm= 1。

MOEA/D:权值向量数量N= 1000，邻居向量数量B= 20，终止种群代数tmax= 100，交叉分布指数ηc= 1，变异分布指数ηm= 1。

在本算例中，独立运行NSGA-Ⅱ、SPEA2和MOEA/D 各30次。所求得Pareto 集合的相关统计数据如表2，其中第2 栏为三种算法所求得的Pareto 集合的Convergence 均值，第3～7 栏为获得的在不同武器消耗区间的非支配解的次数。

表2 NSGA-Ⅱ、SPEA2和MOEA/D在30次独立运行下Pareto集合统计数据Tab. 2 Statistics of Pareto sets obtained by NSGA-Ⅱ，SPEA2 and MOEA/D in 30 independent runs

在表2中，首先由Convergence指标一栏可知，三种算法对于历史最优解的逼近能力为:SPEA2＞NSGA-Ⅱ＞MOEA/D，其中SPEA2 略优于NSGA-Ⅱ，MOEA/D 与另两种算法差距较大。其次由先验信息和仿真结果可得知，本算例理论Pareto 集合的容量为29，即满足约束的武器消耗的下限为2，上限为30。在30 次运行中获得的Pareto 集合完整性指标中，NSGA-Ⅱ有19例位于［16，20］区间；SPEA2有17例位于［21，25］区间，2例位于［11，15］区间；而MOEA/D 下大部分集合容量都小于10。且NSGA-Ⅱ和SPEA2 可以确保所求得的非支配解均为可行解，在MOEA/D 下得到了6个非可行解。综合以上Pareto集合的收敛性、完整性和可行性，SPEA2略优于NSGA-Ⅱ。

为了直观地给出三种算法在不同的武器消耗区间的搜索能力，图3 给出了三种算法在30 次独立运行中非支配可行解的不同武器消耗下的分布。

图3 NSGA-Ⅱ、SPEA2和MOEA/D在30次独立运行中非支配可行解在各武器消耗下的分布Fig. 3 Distribution of feasible non-dominated solutions of different weapon consumption obtained by NSGA-Ⅱ，SPEA2 and MOEA/D in 30 independent runs

除表2 和图3 给出各算法下Pareto 解集分布性的定性比较外，图4 定量比较了NSGA-Ⅱ、SPEA2 和MOEA/D 的各项性能指标。在各算法独立运行30次的前提下:图4（a）为各算法Convergence 均值随进化代数的变化曲线；图4（b）为各算法下Convergence 值的盒图分布；图4（c）表示各算法在不同武器消耗下的目标期望生存价值均值，即CMWTA模型中目标函数f1均值；图4（d）～（f）分别为三种算法两两比较的Coverage 指标的盒图分布。

如图4（a）所示，MOEA/D 在CMWTA 模型中的搜索能力明显弱于NSGA-Ⅱ和SPEA2。虽然NSGA-Ⅱ和SPEA2 在50代后的表现较为接近，但SPEA2 拥有更高的收敛速度和更优的Convergence 值。在图4（b）中，SPEA2 下Convergence 值的整体分布优于NSGA-Ⅱ，但NSGA-Ⅱ较SPEA2 拥有更小的离散度。在图4（c）中，SPEA2 在武器消耗为［6，15］区间内略优于NSGA-Ⅱ，而MOEA/D 曲线出现的震荡和间断表明MOEA/D 在保证在Pareto 前沿面的完整性方面表现较差。在图4（d）～（f）中，除了MOEA/D 在Coverage 方面明显落后于其他算法外，NSGA-Ⅱ和SPEA2表现相当。

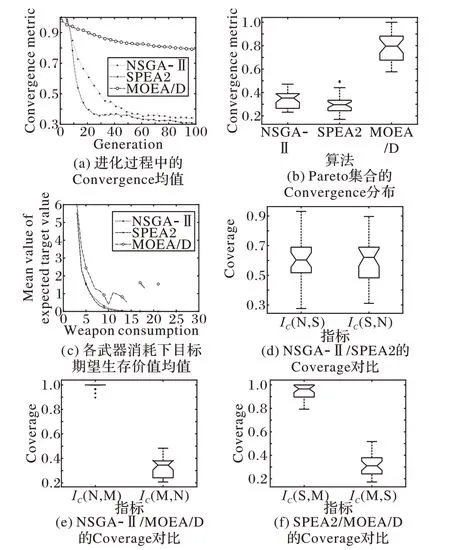
图4 NSGA-Ⅱ、SPEA2和MOEA/D算法下相关性能指标对比Fig. 4 Related performance metrics comparison of NSGA-Ⅱ，SPEA2 and MOEA/D algorithms

综合分析图4中的各项结果，从CMWTA模型的数值求解出发，各算法的寻优能力为:SPEA2＞NSGA-Ⅱ＞MOEA/D。虽然MOEA/D 在求解无约束点对点MWTA 问题时表现较好，但由于CMWTA 中的点对面攻击和多约束的特点，缺乏对改进目标函数、分解策略和约束处理方法三者系统性的研究，因此直接应用MOEA/D求解CMWTA问题效果较差。

而在比较NSGA-Ⅱ和SPEA2 算法求解CMWTA 模型时，需要注意的是，由图4（c）可知，当武器使用数量达到15后，继续增加武器消耗的边际收益极小。结合图4 中NSGA-Ⅱ在武器消耗小于20时的明显优势，可得出结论:在CMWTA 模型中，虽然SPEA2 在Convergence 的数值和离散度上优于NSGA-Ⅱ，但主要优势在于保证武器消耗大于20 的非支配解的完备性。但从实际作战的效费比考虑，高武器消耗下的非支配解并非CMWTA 模型中的求解重点，而由图5（b）和5（d）可知，NSGA-Ⅱ在求解低武器消耗下的CMWTA 问题时具有更好的鲁棒性。因此从指挥控制系统的辅助决策考虑，NSGA-Ⅱ可能更具有实际应用价值。

为了更直观地说明以上结论，选取NSGA-Ⅱ和SPEA2 在30 次运算中获得的部分武器消耗下的最优解，通过图5 进行部分可视化显示。

在图5中，由“×”标出各武器瞄准点并显示相应的杀伤范围，箭头所指目标为具有毁伤门限要求的目标，箭头起始处第一个数字代表该目标当前生存概率，括号后的数字代表满足毁伤门限时的最大生存概率，“-”连接的是偏好指派的武器-目标对wi-tj，aij= 1。由图5（a）和5（e）可看出，当武器使用数量为3 时，武器分布在两个区域，在左上角区域中，要求威胁目标6 的生存概率小于0.2，目标14 具有强制指派武器Ⅲ的要求，且目标6 和14 距离安全目标1 较近。此时NSGA-Ⅱ和SPEA2 均选择一武器协同武器Ⅲ完成上述任务，此时协同武器的杀伤范围不宜过大，否则难以满足对目标6 的杀伤门限。NSGA-Ⅱ倾向于使用协同武器覆盖目标8 和19，而在SPEA2下选择攻击威胁权值更高的目标4、10、16 和19，使得适应度达到4.204 0，显然SPEA2 下的方案更优。在右下角区域，目标13 具有0.1 的期望生存概率要求且距离安全目标2 较近，NSGA-Ⅱ通过利用合适杀伤范围的武器在规避安全目标2 的同时覆盖右下角多目标，且使得目标13 的期望生存概率为0.05，而SPEA2 下覆盖目标较少，且目标13 的期望生存概率刚达到0.1，此时NSGA-Ⅱ的决策明显更优。同理，在其他武器消耗下求得的最优方案均能较好地满足作战需求。从图5中可以看出，当武器数量较少时，各算法求得的方案对于武器杀伤范围和作用区域的选择具有较高的相似性。而随着武器使用数量的上升，差异性越来越明显，并且当武器使用数量达到10 时，已对所有目标都进行了火力覆盖，继续增加武器消耗的边际收益不断降低。在本算例中，综合考虑最大化期望作战效率和效费比。建议将武器使用数量设为12或13。

图5 NSGA-Ⅱ和SPEA2在30次独立运行中最优非支配解的可视化对比Fig 5 Visualization comparison of optimal non-dominated solutions obtained by NSGA-Ⅱand SPEA2 in 30 independent runs

算例2 本算例对本文中的进化操作和修复算法进行验证。基于算例1中的参数设定，采用如下3种实验设定:1）初始种群经过选择、交叉、变异、修复进化操作后生成等规模的精英种群，分析对比两个种群的适应度分布、多样性保持等统计数据；2）基于算例1中的参数设定，对比分析未修复/修复下的种群个体的适应度f1和约束违反值；3）分别对比分析未修复/修复下NSGA-Ⅱ、SPEA2和MOEA/D算法的仿真结果。

对比结果如图6所示。图6为初始种群经过交叉、变异、修复后的相关统计数据。其中图6（a）为各武器消耗下初始化种群和子代种群的解分布对比，图6（b）为各武器消耗下初始化种群和子代种群的目标期望生存价值的均值对比，图6（c）为各武器消耗下初始种群和子代种群的约束违反值的均值对比。

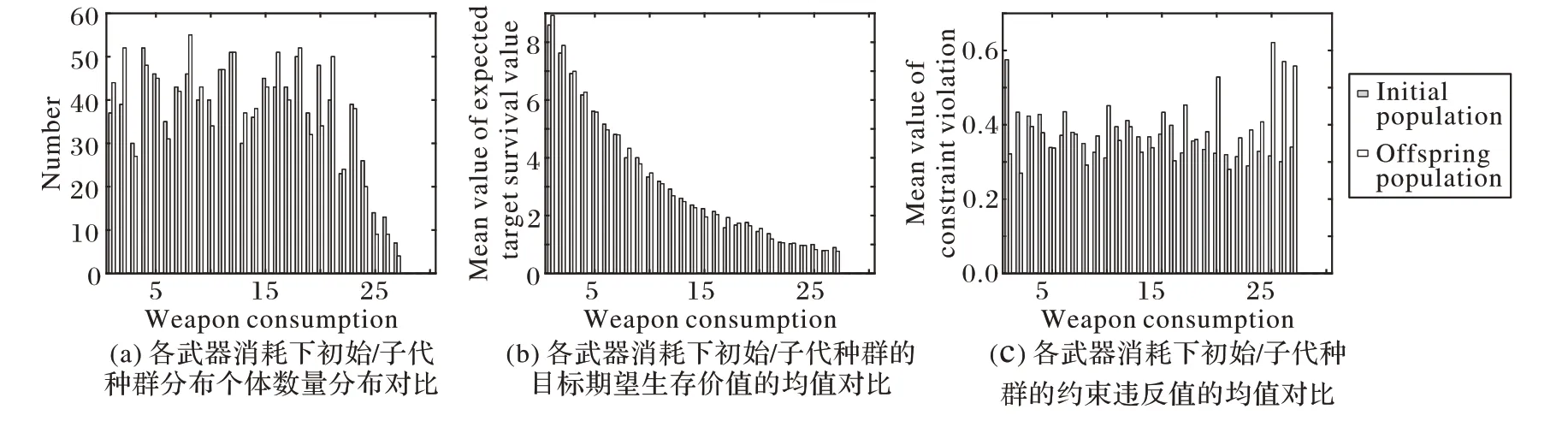
图6 交叉、变异、修复下初始种群与子代种群的统计数据Fig. 6 Statistics of initial population and offspring population by crossover，mutation and repair

如图6（a）所示，在本文提出的交叉、变异、修复策略下后，子代种群与随机化的初始种群的个体分布相近，可见本文所提出的交叉、变异等进化操作未影响初始种群的多样性分布。在图6（b）中，子代种群的目标期望生存价值的均值在武器消耗小于9 时高于初始种群，大于9 时低于种群。在图6（c）中，低武器消耗下，如武器消耗为1、2 时，子代种群的约束违反值的均值有明显改善，而在个别武器消耗大于25 时，子代种群的约束违反值的均值出现大幅上升。并且，在种群适应度均值上，初始种群为2.841 7，子代种群为2.833 1；在种群约束违反值均值上，初始种群为0.326 4，子代种群为0.356 3。综上可见，种群适应度均值略有下降，种群多样性增加，其原因在于低武器消耗下的可行解比例增大，高武器消耗下的约束违反值均值增加。结合算例1 中得到的建议最大武器消耗量为12和13的结论，可见本文提出的交叉、变异、修复策略的合理性。

图7为未修复/修复下不同武器消耗个体的目标期望生存价值的均值对比图。如图7 所示，修复后各武器消耗个体的适应度均值均得到了提升。

图7 未修复/修复下各武器消耗个体的目标期望生存价值均值Fig. 7 Mean value of expected target value of different weapon consumption under non-repair/repair strategies

图8为未修复/修复下不同武器消耗个体的各约束违反值的均值对比图，其中图8（a）～（c）分别为未修复/修复下安全规避、毁伤门限和偏好指派的约束违反值对比图。

如图8所示，修复后各武器消耗个体的适应度均值均得到了提升。由图8（a）可知，修复后安全规避约束违反值反而上升，其原因在于修复算法中未有对安全规避约束的修复机制。但由于该约束结构简单，违反值仅与‖S-C‖成正比关系，因此完全可交由进化算法的“优胜劣汰”选择机制进行优化。在图8（b）中，修复算法中对毁伤门限约束的修复使得该违反值得到大幅降低。在图8（c）中，偏好指派约束修复使得该违反值在武器消耗达到8后才有明显降低，其原因在于为了保持种群多样性，偏好指派只在偏好武器被使用的个体中进行修复，而在随机生成的初始种群中，武器消耗越少，偏好武器被使用的概率越小，反之武器消耗越大，修复算法对偏好指派约束的修复效果越明显。且综合图7和8可知，修复后的种群中不存在武器消耗为29、30的个体，这是由于在初始化种群中武器消耗越大时，越易造成无效武器使用，而修复算法中的一致性修复会对此类武器进行修剪，因此修复算法在也一定程度上限定了合理的武器消耗上限。

表3 为未修复/修复NSGA-Ⅱ、SPEA2 和MOEA/D 算法下的Pareto 集合的统计数据。在表3 中，个体修复算法将NSGA-Ⅱ、SPEA2 和MOEA/D 的Convergence 值均提升了20%以上，其中未修复的NSGA-Ⅱ和SPEA2 在100 代时的Convergence 均值几乎相等。同时个体修复算法也明显提升了NSGA-Ⅱ和SPEA2 算法所求得的Pareto 集合的完整性，未修复NSGA-Ⅱ求得的Pareto 集合主要分布在16～20 区间，而修复后有11 例分布在［21，25］区间，同样修复SPEA2 算法下的Pareto 集合也有17 例在［21，25］区间。但修复策略对MOEA/D 影响较小，略微提高了Pareto 集合的大小，但不可行解也由1个上升到6个。

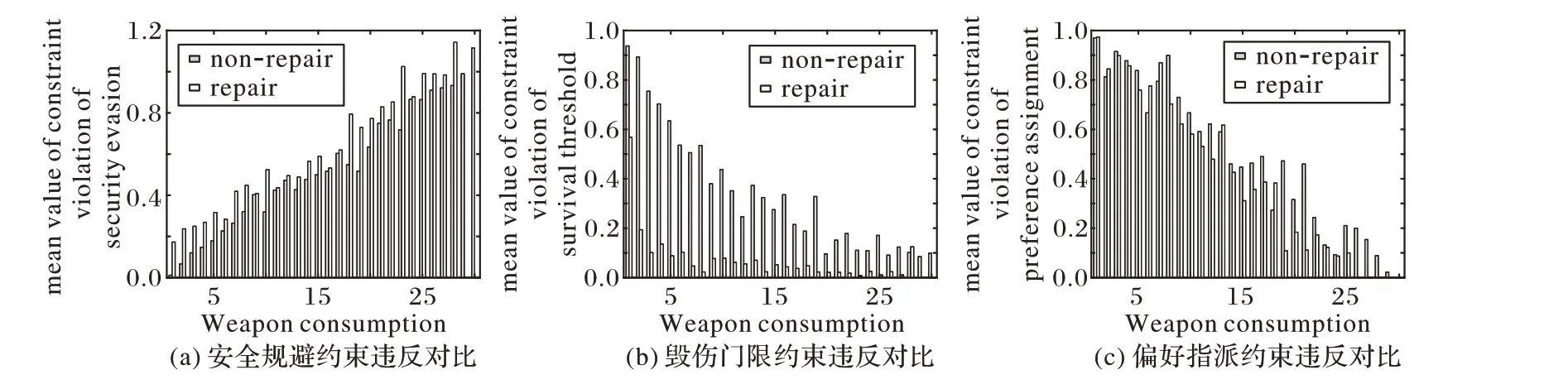
图8 未修复/修复策略下各武器消耗下各约束违反对比Fig. 8 Constraint violation comparison of different weapon consumption under non-repair/repair strategies

表3 NSGA-Ⅱ、SPEA2和MOEA/D在修复/未修复策略下独立运行30次获得的Pareto集合统计数据Tab. 3 Statistics of Pareto sets obtained by NSGA-Ⅱ，SPEA2 and MOEA/D algorithms in 30 independent runs under non-repair/repair strategies

为了直观地分析个体修复算法对非支配解分布性的影响，图9 给出了各算法在修复和未修复两种策略下30 次独立运行获得的各武器消耗下非支配可行解个数。在NSGA-Ⅱ算法中，修复算法增强了对武器消耗大于12 的非支配解的搜索能力。在SPEA2算法中，未修复版本在武器消耗小于18时略有优势，但当武器消耗大于25 时，已无法求得相应的非支配解，而修复算法的搜索能力在武器消耗达到18 后大幅反超未修复版本，且求得的非支配解相应的武器消耗可达到29。相似地，当武器消耗达到6 后，修复MOEA/D 算法的搜索能力反超未修复MOEA/D 算法。通过以上结果，可知本文提出的个体修复算法可以有效提高CMWTA 问题中Pareto 集合的分布性，且对SPEA2算法的提升更大。

图10 比较了未修复/修复NSGA-Ⅱ、SPEA2 和MOEA/D 算法的各项性能指标。各算法独立运行30次。图10（a）为各算法下Convergence 均值随进化代数的变化曲线；图10（b）为各算法求得的Pareto 集合的Convergence 值盒图分布；图10（c）为各算法在不同武器消耗下的目标期望生存价值均值；图10（d）～（f）分别为每种算法下修复和未修复版本进行Coverage对比的盒图分布。

图9 NSGA-Ⅱ、SPEA2和MOEA/D在修复/未修复策略下独立运行30次获得的非支配可行解在各武器消耗下的分布Fig. 9 Distribution of feasible non-dominated solutions of different weapon consumption obtained by NSGA-Ⅱ，SPEA2 and MOEA/D algorithms in 30 independent runs under non-repair/repair strategies

图10 NSGA-Ⅱ、SPEA2和MOEA/D在修复/未修复策略下相关性能指标对比Fig. 10 Performance metrics comparison of non-repair/repair of NSGA-Ⅱ，SPEA2 and MOEA/D algorithms under non-repair/repair strategies

如图10（a）所示，在每种算法下，修复后Convergence 值的收敛速度下降，但最优值得到了明显提升，其中未修复NSGA-Ⅱ和SPEA2在100代时几乎收敛到同一点。未修复SPEA2在进化初期存在一个急剧的下降阶段，随后开始缓慢上升，而其他算法处于单调下降趋势，其原因在于各算法下种群不同的搜索选择机制。由于CMWTA 模型中多约束的存在，使得算法进化初期可行解更易被输出为非支配解，而NSGA-Ⅱ初期选择的可行解数量较少，但适应度较高，在后续进化过程中更可能被作为非支配解输出，从而表现为Convergence 值的单调递减。而SPEA2 在进化初期可以搜索到较多的可行解，此时Convergence 值会快速下降，但随着进化过程的推进，初期的可行解一旦被新搜索到的解支配，则不具备被选择优势，此时Pareto 前沿面由多个可行解退化为数量更少适应度更高的非支配解，表现为Convergence 值的缓慢上升。由图10（b）可知修复算法使得各算法的收敛性得到了增强。在图10（c）中除MOEA/D 外，修复算法进一步优化了其他算法中各武器消耗量下的目标期望生存价值均值。根据图10（d）～（f）可知，修复算法在和对应的未修复算法进行Pareto 集合的Coverage 对比时具有明显优势，且对SPEA2的提升更为明显。

根据以上分析，本文提出的个体修复算法使得NSGA-Ⅱ、SPEA2 和MOEA/D 在非支配解的分布性、适应度和Pareto 集合的收敛性方面均有明显提升。

4 结语

综上所述，本文提出的武器-目标分配问题可作为基于重叠目标分群的攻击模式研究。在威胁评估过程中，若可对目标执行基于物理位置的目标分群，则可综合考虑武器资源、杀伤范围、目标类型和地形等因素，解得约束可行区域内的Pareto集合，以供决策者选择。

本文建立了基于以上作战需求的CMWTA 模型，在多目标进化算法框架下采用个体编码、检测修复和约束支配相结合的方式处理约束条件，并设计针对多目标WTA 问题的Convergence指标，对NSGA-Ⅱ、SPEA2和MOEA/D 三种求解框架进行了仿真对比，对个体修复算法进行了仿真验证。随着战场环境的日益复杂，以特定的作战需求为出发点，进行相应的模型和算法设计是未来WTA问题的研究方向。