面向二类区分能力的干扰熵特征选择方法

曾元鹏，王开军，林 崧

（1. 福建师范大学数学与信息学院，福州350007； 2. 福建师范大学数字福建环境监测物联网实验室，福州350007）

（*通信作者电子邮箱wkjwang@qq.com）

0 引言

特征选择是数据挖掘的预处理步骤，旨在通过删除不必要特征，以达到降低算法复杂度、提高算法性能的目的。特征子集的评价准则或启发式确定后，特征选择问题从某种意义上来说就是在特征空间中搜索最优特征子集问题［1］。

近年来，使用信息熵方法［2］来进行特征选择越来越成为广大研究者的研究热点。文献［1］提出将粗糙集相对分类信息熵作为适应度函数实施粒子群算法进行特征选择；文献［2］采用基于互信息的近邻熵进行近似的最近邻前向搜索来选择特征（Neighborhood Entropy Feature Selection，NEFS），并通过优化索引结构提出单索引近邻熵特征选择（Single-indexed Neighborhood Entropy Feature Selection，SNEFS）方法来选择更好的分类特征。互信息在相关性分析上有计算简单、可解释性强特点，因此基于互信息的特征选择方法被广泛应用于特征选择［3］。相关性最大冗余性最小特征选择（feature selection based on Max-Relevance and Min-Redundancy，MRMR）算法［4］计算待选特征与类别的互信息、待选特征与已选特征间的平均互信息，以两者的差值是否为最大值来决定该特征可否加入最优特征子集中；但是该方法没有对特征数据在类别上的分布情况作出合适判断，无法体现出数据的混乱情况。与MRMR方法类似的还有文献［5］提出的特征排序方法，度量特征间的独立和冗余程度，考虑了特征子集中不同特征间的多变量关系。文献［6］运用了互信息将特征进行排序，将排序后的特征逐个加入特征子集进行分类，去掉每次可以正确分类的样本，从而避免信息的冗余。联合互信息（Joint Mutual Information，JMI）方法［7］选取信息增益最大的特征作为第一个特征；接着计算待选特征的信息增益；然后，计算在已选特征子集条件下，待选特征与类别的条件互信息均值；最后，将两者之和最大的待选特征加入已选特征子集；该方法在不同类别数据的区分能力上存在欠缺。与该方法部分类似的有文献［8］提出在特征和类别之间的联合最大信息熵方法度量特征子集并用粒子群优化方法来搜索最优特征子集。Relief方法［9］提出先随机选取一个样本点，并从同类中寻找最近的样本，再寻找最近的非同类样本计算其距离，如果同类距离较小，则认为该特征对区分不同类别样本更有能力，增加该特征的权重；该方法以近邻的方式去判断二类的区分性，未从数据分布的整体情况进行考虑。文献［10］提出以相对分类信息熵作为适应度函数度量特征子集的重要性，使用遗传算法搜索最优特征子集；文献［11］假设特征之间相互独立，使用特征与标签集合之间的信息增益来衡量特征与标签集合之间的重要程度，然后采用信息增益阈值选择特征。文献［12］在K-近邻互信息的基础上将其扩展至高维，并采用前向搜索和后向交叉相结合的形式来获得最优强相关特征子集。文献［13］利用模糊等价关系将互信息推广至模糊互信息，接着计算该模糊度量下的候选与已选特征的相关关系，最后采用最大最小准则与前向贪婪算法来选出最优特征子集。

现有方法主要测量备选特征和类别之间的信息熵来筛选最优特征，但没有评价某个特征在类别区分上的能力和贡献大小，这造成所选特征的缘由是模糊的、不清晰的。本文方法的好处是对某个特征区分不同类别数据的能力给出了一个明确的评价指标，使得挑选某个特征具有明确的依据和含义。本文提出了一种面向二类区分能力的干扰熵方法（Interference Entropy of Two-Class Distinguishing，IET-CD），对每个特征下两类数据的相互干扰程度采用干扰熵值进行量化，使用干扰熵指标作为不同类别数据区分能力的评价指标，当干扰熵值越小，说明该特征的二类区分能力强，反之则弱，为寻找二类数据区分明显的特征提供了方法。

1 干扰熵方法的相关定义

给定具有n个m维样本的二类数据集D=[d1，d2，…，dm]，含有正类（A 类）样本X和负类（B 类）样本Y。对于数据集D中的di(i≤m)维（特征）上的数据，以样本均值u1较小的一类为正类，样本均值u2≥u1的一类为负类，k个正类样本记为X={X1，X2，…，Xk}，n-k个负类样本记为Y={Y1，Y2，…，Yn-k}，正、负类样本的取值范围为[Xmin，Xmax]与[Ymin，Ymax]，在正类范围内出现的负类样本为Y+={Xmin≤，…，≤，j≤n-k，Y+⊂Y，在负类范围 内的出现正类样本为X-={Ymin≤，…，≤Ymax}，l≤k，X-⊂X。

定义1 混合条件概率。在正类数据取值范围内，出现正类样本X概率为P(X)=k/(k+j)，出现负类样本Y+的概率为P(Y+)=j/(k+j)，则正负类样本出现的联合概率为P(X，Y+)，出现负类样本Y+的混合条件概率为P(Y+|X)，公式如下:

定义2 样本归属正类的概率。设在正类数据范围出现负类样本点（i= 1，2，…，j），混淆区域为[，Xmax]；负类数据 范 围 出 现 正 类 样 本 点（i= 1，2，…，l），混 淆 区 域 为[Ymin，Xi-]。统计在正类混淆区域内的r个正类样本和t个负类样本，正、负类样本出现在混淆区域的概率分别记为P(A*)=r/(r+t)、P(B*)=t/(r+t)。负类样本在正、负类数据的高斯概率密度下属于正、负类的概率记为P()、P()，则样本归属正类概率记为P()，类似地计算出样本归属负类概率P()，公式定义如下:

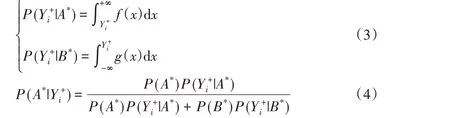
其中:f(x)是具有均值u1和标准差σ1的正类数据高斯函数，g(x)是具有均值u2和标准差σ2的负类数据高斯函数。

在上述混合条件概率P(Y+|X)和样本归属正类的概率P()的基础上，设计混淆概率。

1.2 方法 对照组为常规护理，指导戒烟，预防感冒等。实验组患者在此基础上实施围手术期呼吸运动训练。告知患者围手术期呼吸运动训练的目的和必要性、从而取得患者的配合。训练自患者入院开始每日指导练习。

定义3 混淆概率。在正类范围内，负类样本被误认为是正类样本的混淆概率P(+)为混合条件概率和样本归属正类的概率的乘积，即:

定义4 类间干扰熵。在正类范围内，正类干扰熵H(Y+)为每个负类样本点的干扰熵之和；类似地，在负类范围内，负类干扰熵H(X-)为每个正类样本点的干扰熵之和。类间干扰熵H(Y+，X-)定义如下:

对于二值的离散型特征，设计如下的定义用于计算混淆概率。

定义5 离散特征混合条件概率。对于取值为0、1的离散型特征，设该特征上正类样本集A中值为0和1的样本个数分别为a0和a1，且a0≥a1，负类样本集B中值为0和1的样本个数分别为b0和b1。则值为0的样本x属于正、负类的概率分别为PA(x=0)=a0/(a0+a1)、PB(x=0)=b0/(b0+b1)，则值为1的样本x属于正、负类的概率分别为PA(x=1)=a1/(a0+a1)、PB(x=1)=b1/(b0+b1)。在A中出现值为1和0样本的混合条件概率分别为P(x=1|A)=a1/(a0+a1)、P(x=0|A)=a0/(a0+a1)；同 理 有P(x=1|B)=b1/(b0+b1)和P(x=0|B)=b0/(b0+b1)。

定义6 离散特征的混淆概率和干扰熵。设一个特征上正类样本子集A有a0≥a1，则值为1的样本的混合条件概率与样本归属于正类的概率的乘积称为混淆概率P()=P(x=1|A)PA(x= 1)，同理有混淆概率P(B)=P(x=0|B)PB(x=0)。则干扰熵定义为H(A-，B+)=H(B+)+H(A-)，其中H(B+)=

2 面向二类区分能力的干扰熵方法

面向二类区分能力的干扰熵方法以类间干扰熵来衡量该特征所包含的两类数据混淆情况。对于二类数据集中的某一维度/特征，若类间干扰熵大，说明两个类别的数据混合程度大，二类区分性弱；若小，说明两个类别的数据混合程度小，二类区分性强。

当负类样本出现在正类数据范围内时，正负样本的数据范围出现重叠，使二类数据的区分度减弱。正类数据范围内的负类样本数量对特征二类区分能力的影响采用定义1 或5的混合条件概率进行量化计算。

混合条件概率衡量了在正类数据范围内混入负类样本的数量情况，样本归属正类的概率考虑到混入的负类样本归属于正类的程度，将上述概率的乘积作为两类数据的混淆情况的量化，通过定义3或6的公式得到相应的混淆概率。

评价一个特征的二类区分能力的干扰熵方法步骤如下:

依据上文的定义，对于连续型数据有:

1）选择数据集D中的一个特征，分别计算正、负类样本的取值范围，统计正类范围内的负类样本。

2）计算正类数据范围内正、负类出现的概率P(X)、P(Y+)，联合概率P(X，Y+)，以及混合条件概率P(Y+|X)。

3）在正类数据范围内，计算样本归属正类的概率P()。对称地，在负类数据范围内，计算样本归属负类的概率P()。

4）计算正类数据范围内的负类样本被误认为是正类样本的混淆概率P()。对称地，在负类数据范围内，计算正类样本被误认为是负类样本的混淆概率P()。

5）依据混淆概率计算类间干扰熵H(Y+，X-)。

对于离散型数据，类似地依据上文的定义计算混淆概率和类间干扰熵。

3 实验分析

为了检验本文IET-CD 方法的有效性，利用IET-CD 方法计算每个特征的类间干扰熵，按熵值从小到大排序，选取熵值小（二类区分程度大）的特征组成特征子集，将该特征子集用于评价一个特征二类区分能力的实验。类似地，5 个对比方法——NEFS、SNEFS、MRMR、JMI、Relief特征选择算法也给出特征排序结果，取排序位置最前的几个特征组成特征子集，用于二类区分能力的分析。

实验选取3个UCI（University of California Irvine）［14］数据集Sonar、WDBC（Wisconsin Diagnostic Breast Cancer）、Ionosphere和4k20lap 模拟基因表达数据集［15］进行测试，其中4k20lap1_2是4k20lap 数 据 集 中 的 第1 和2 类 组 成。Sonar、WDBC、Ionosphere、4k20lap1_2数据集的对应的样本数分别是208、569、351、134，特征数分别为60、30、34、20，类别数均为2。本实验的特征选择算法（IET-CD）的实现代码由作者使用Python语言编写。对比方法相关性最大冗余性最小方法（MRMR）、联合互信息方法（JMI）、Relief 程序来源于Matlab 的FEAST（FEAture Selection Toolbox）工具箱，这3个方法参数均采用工具箱默认参数。NEFS与SNEFS算法代码来源于文献［2］，并设定特征近邻参数为4。最后选取各方法所得前5个最优特征进行实验。

本实验通过计算特征的干扰熵来衡量该特征中两类数据的分离/重叠程度，干扰熵值越小，特征区分能力（分离程度）越好。使用特征的数据散点图来验证以干扰熵值作为评判标准的特征区分能力的正确性，横坐标表示样本编号，纵坐标表示样本值。

在不同的数据集上对5个不同的特征选择算法所选特征的进行干扰熵的计算，实验结果包含对应的数据集、特征选择算法、所选特征中前5个特征的编号，所选特征对应的熵值，用于对比的配对特征、本文方法获胜情况，见表1。图1 和图2 列出Sonar、WDBC对比特征散点图用于验证本文方法的正确性。

图1 Sonar数据集对比特征的散点图Fig. 1 Scatter plot of contrast features comparison on dataset Sonar

表1 4个数据集上各方法所选特征的二类区分能力对比Tab. 1 Two-class distinguishing ability comparison of selected features of each method on four datasets

图2 WDBC数据集对比特征的散点图Fig. 2 Scatter plot of contrast features comparison on dataset WDBC

从表1可知，在Sonar数据集上，10号特征比11号特征的干扰熵值小，反映出10号特征二类区分能力强，通过对比图1中的数据散点图，可看出10号特征比11号特征的数据重叠区域小，验证了干扰熵值小其二类区分能力强。对11号特征与59号特征进行对比，11号特征获胜，在图1数据散点图中也反映了11号特征数据重叠区域小，混淆程度小，说明本文IET-CD方法的性能优于对比方法。

WDBC 数据集上的27 号和22 号特征，Ionosphere 数据集上的6 号和4 号特征的情况与Sonar 数据集上的48 号和9 号特征情况相似，两个特征的干扰熵值相差较小，说明两个特征的二类区分能力相近，通过相应的散点图反映的结果可以看出，特征的数据重叠情况相近，验证了干扰熵值相近的两个特征的二类区分能力相似，故对比结果表现相同。对表1 中的WDBC数据集上的5号与20号特征对比，20号特征获胜，说明20 号特征的二类区分能力强，从图2 的数据散点图可看出20号特征的数据重叠区域小，逆向验证了20 号特征干扰熵值小，5 号特征干扰熵值大，以此证明干扰熵值能正确反映二类数据的区分程度。

表1 中的Ionosphere 数据集和4k20lap1_2 模拟基因数据集仍以相同的方式进行对比，故不再一一列出对应的散点图。因为4k20lap1_2模拟基因数据集的部分特征二类样本混淆数量较少，所以在该数据集上反映出的特征干扰熵值也相对较小，符合干扰熵的定义。4k20lap1_2 模拟基因数据集的3 号特征比15 号特征的干扰熵值小，表明3 号特征的二类分区能力强。因3 号特征的不同类别数据分离情况较好，15 号特征的不同类别数据混合程度比3号特征混乱，故3号特征的区分能力胜过15 号特征。由表1 中的配对特征的对比结果可看出，3号特征的区分能力胜过15号特征，其特征对应的干扰熵值能正确反映二类数据的区分程度。其他特征类似对比，并通过散点图可验证其结论的正确性。

4 结语

本文通过计算特征的二类干扰熵来进行数据区分能力的判断从而进行特征选择，选出区分能力较好的特征。干扰熵值越小区分能力越强，干扰熵值越大区分能力越弱，该方法能有效筛选二类混合程度大、区分度不明显的特征，发现二类区分能力好的特征，为识别特征的二类区分能力提供了评价指标。