改进迁移算子的BBO算法及其在PID参数中的优化

裴 沛，李彩伟，吕波特

（1. 北京中油瑞飞信息技术有限责任公司，北京100029； 2. 国家工业信息安全发展研究中心，北京100040；3. 北京博华信智科技股份有限公司，北京100029）

（*通信作者电子邮箱licaiwei888@sina.com）

0 引言

进化算法常用于求解显式和隐式函数的极值。与数值求解方法不同，进化算法无需知晓目标函数是否可微。实际上，进化算法不需要目标函数的相关信息。由于这一特性使它们成为一种解决复杂问题的方法［1］。

生物地理学优化（Biogeography-Based Optimization，BBO）算法［2］是由美国的Simon 基于生态系统中各个种群在不同栖息地之间的迁徙、突变、灭绝的一般规律提出，算法可用于函数求解与全局参数优化。BBO 算法也属于一种进化算法，因对生物在生态系统中的进化机制进行了模拟，具有计算量较小、算法参数少、收敛速度快等特点［3］。

近年来，BBO 算法中涉及的进化机制也已被大量学者进行了研究，研究结果表明，其他进化算法中存在的搜索能力下降现象，在BBO 算法中也同样存在［4-6］。为解决这个问题，很多学者对BBO 算法从生物地理学原理出发进行了改进。江岳春等［7］将余弦型迁移模型、差分进化算法的变异策略以及动态非均匀变异算子引入生物地理学优化算法，并将其用于求解风电-水电互补优化运行策略的模型，结果表明经改进的BBO 算法比粒子群算法和遗传算法寻优能力更强，求解的模型精度更高。张文辉等［8］提出了自适应迁移算子和差分进化变异算子，对BBO 算法进行改进，改进算法在保留了栖息地特征的同时，也改善了栖息地间信息交流以及分享的情况，实验结果表明改进后的BBO 算法全局优化能力得到了进一步增强。陈道君等［9］的研究表明使用柯西分布比高斯分布更易产生远离原点的随机数，将其用于改进变异算子能增强BBO算法的全局搜索能力。鲁宇明等［10］提出了二重迁移算子和二重变异算子，使得个体在进化中的进化概率更高，并使改进后的BBO 算法全局寻优能力得到进一步提升。Zhang 等［11］将模糊C均值算法和BBO算法结合，用于图像分割，得到的混合算法较其他算法更优。文献［12］基于生物地理学算法，提出一种混合迁移多目标优化算法，并在ZDT测试函数进行验证，表明算法在收敛性和搜索能力方面更优。

以上基于生物地理学原理的改进提升了算法寻优能力，但也在一定程度上增加了算法的复杂性，收敛精度方面仍有待进一步提升。

为加快算法的收敛，并提高算法的收敛精度，避免算法陷入局部最优，本文提出了一种基于改进迁移算子的生物地理学 （Improved Migration Operator Biogeography-Based Optimization，IMO-BBO）算法。结合“优胜劣汰”的进化思想，将自然环境的变化作为影响因素，对不适宜迁移的个体进行淘汰并重新生成。同时引入多种群概念，促使不同种群之间的物种进行信息交互，能很好地增强算法的全局勘探能力。将本文提出的IMO-BBO算法在13个基准测试函数进行测试，结果表明改进算法在大部分测试函数中的全局探索能力、收敛速度和收敛精度上都有显著提高。经IMO-BBO 算法整定后的PID（Proportional Integral Differential）控制器也得到了更快的响应速度和更稳定的精度。

1 BBO算法原理

BBO 算法来源于生物地理学理论，如图1 所示，每个栖息地都有对应的适宜度指数（Habitat Suitability Index，HSI），其中待优化问题中可能存在的解实际由栖息地进行表示，栖息地质量的优劣由HSI 来进行表示。影响HSI 的因素包括降雨情况、空气湿度、环境温度、植被多样性等，各种影响因素通过一个适宜度向量（Suitable Index Variable，SIV）来对栖息地进行描述。

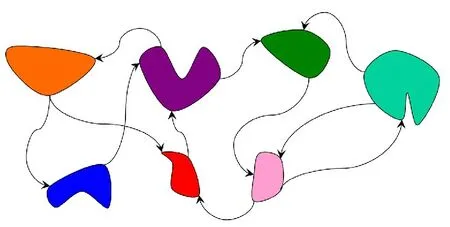
图1 BBO多个栖息地以及迁移过程Fig. 1 Multiple habitats and migration processes of BBO

物种的迁移主要与HSI 有关。较优的HSI 表示栖息地物种多样性较好；较差的HSI表示物种多样性受到限制。当HSI较优时，表明栖息地物种数目趋向于饱和，接近栖息地最大容量，会存在较多的物种迁出的现象。而当HSI 保持较差水平时，又会有较多的物种迁入此栖息地［13］。同时，BBO算法对栖息地中可能发生的突发事件进行模拟，使物种的一部分特性发生改变，即令栖息地的物种产生一定程度的突变。各个栖息地间，BBO 算法利用迁移和变异操作［14］增强了物种间的信息交互，使得物种多样性得到了一定程度的提升。

2 改进的BBO算法

本文受文献［15］中生物寄生“优胜劣汰”进化思想的启发，考虑了自然环境等因素对个体迁移过程的影响，提出一种改进的BBO 算法。本文对迁移算子进行了改进，将个体的迁移距离作为影响因素，使不适宜迁移的个体越容易被新个体替换。同时为丰富种群的物种多样性，进一步加快算法的收敛速度，引入双种群概念。

2.1 迁移算子的改进

不同栖息地间物种迁移主要有周期性和非周期性之分，周期性主要与繁殖、食物、气候变化等因素有关，非周期性主要由自然灾害引起，与生存条件的恶化有关。

当栖息地Xi中的个体迁移至其他栖息地Xj时，其迁移距离d(Xi，Xj)由式（3）的欧氏距离公式得到。

其中:xi，1为第i个栖息地的第1个个体，n为种群数量大小。

根据栖息地之间的迁移距离进行排序，得到从Xi迁移至不同栖息地的距离系数Wi，迁移距离越远距离系数大，迁移距离越近系数越小。

当迁移距离增大，个体迁移至目的地所需能量和时间更多，受自然环境等影响而被其他个体替代的可能性越高；当迁移距离越小，个体在迁移过程中只需用更少的能量和更短的时间，因此被替换的可能性相应越小。

另一方面，考虑到优质解本身更有可能是全局最优解，为避免迁移过程中造成优质解的退化，对优质解增加保护措施。个体迁移过程中，被替换的概率按以下公式计算得到:

其中:Pi，j为从栖息地i迁移至栖息地j的个体替换率；wi为迁移过程中的距离系数，wmax为距离系数最大值，与种群数量有关；HSIi为第i个栖息地的适应度值，HSImax为所有栖息地中适应度的最大值。

算法迭代过程中，在保持原先群体大小和开发能力不变的情况下，进一步提高算法对可行解区域的探索能力。本文引入差分进化策略产生新个体，可在一定程度上保证群体的多样性。新个体生成方式如式（6）所示:

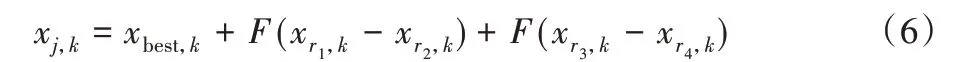
其中:xbest，k为当前最优解的第k个个体，xr1，k、xr2，k、xr3，k、xr4，k为随机选择的4个不同个体。

由式（6）可知，新个体的信息由最优解和两个差分公式计算得到。而且缩放系数F可以对探索和开发能力进行平衡。当F=0时，新个体直接获取最优个体的信息，提高了算法的开发能力。当F增大时，新个体从其他个体获取的信息逐步增加，使算法在探索可行解的能力上增强，但相对地会弱化最优解的开发能力。为平衡对局部和全局的搜索能力，本文选取F=0.5。

2.2 多种群协同策略

多种群［16］是将多个种群按照不同或相同的初始环境和约束条件，各自独立进化，是一种保持种群多样性的有效方法。多种群策略在其他算法中得到了大量研究和使用［17-20］，但鲜有在BBO算法中使用的报道。

多个种群进化过程迭代到一定次数时，按一定条件对种群间的个体信息进行交流和协作。因各个种群在进化时具有独立性，能较好地保证种群多样性。同时不同种群间优秀个体的信息参与信息交换可以提高收敛速度。

常见的协作算子有长方体交叉算子、离散交叉算子、两点交叉算子、算术交叉算子等［21］。本文采用双种群的协同策略，选择算术交叉算子为协作算子。种群间的交叉概率由概率pc决定，若满足rand(0，1)＜pc，则执行协作算子操作；否则不执行协作算子。

在IMO-BBO 算法中，当使用算术交叉算子对种群1 中的个体Xi进行操作，需从种群2 中选择当前HSI 最小的个体Xj，即适应度最佳的个体，按以下公式计算得到新的个体:

其中:r为交叉因子，X′i和X″i分别表示计算得到的新个体。若新个体比原个体Xi具有更好的适应度，则将原个体进行更新。当在种群2应用协作算子时，则选取种群2的各个个体与种群1 的最优个体执行协作算子操作，以生成新的个体。通过将种群中的个体与其他种群的适应度最佳的个体进行信息交互产生的两个新个体，能更好地丰富种群多样性，促进种群的进化。

2.3 算法基本流程

IMO-BBO算法的算法流程如图2所示。

图2 改进BBO算法流程Fig. 2 Flow chart of improved BBO algorithm

具体步骤如下:

1）设定IMO-BBO相关参数，初始化种群数量、迭代次数、栖息地的突变率、栖息地的适宜度向量SIV。

2）分别设定种群1 和种群2 的参数，初始化交叉概率pc、交叉因子r。

3）计算栖息地中物种的迁入迁出概率。

4）执行改进的迁移操作、变异操作。

5）当种群1 和种群2 分别将此次迭代步骤的3）～4）都执行完毕，执行协作算子。结合各个种群的交叉因子r，计算得到新的个体，若新个体的HSI 值更小，则将原个体更新为新个体。

6）判断是否满足终止条件，若不满足，则继续执行步骤7；否则输出计算结果，并退出。

7）分别更新种群中的精英个体，并使用精英个体替换掉种群中适应度最差的n个个体，并重复执行步骤3）～6）。

虽经协作算子进行个体信息交互后的个体不一定最优，但是这样的个体为种群提供了更多可能性，与BBO 算法的变异操作相比，在寻找最优解方面有效性更高，从而提高了对求解问题的收敛速度。

3 改进算法在PID参数优化中应用

在工业的过程控制领域，PID 控制策略在控制系统中所占的比例超过90%，而所配置PID 参数会直接影响到系统运行的性能和稳定性，因此获取一组合适的PID 参数非常关键。随着群智能算法等人工智能算法的迅速发展，很多新的参数优化方法也被用于PID 控制器参数的整定。其中，文献［22］根据种群内相似度调整变异算子，提出一种自适应变异的差分进化算法，并成功应用于PID 参数整定优化。本文中的改进BBO 算法也属于群智能优化算法的一种，由于其收敛精度高、寻优性能稳定的特点，能很好地对PID 控制器的参数进行寻优。

PID控制器的公式可以由式（9）表示:

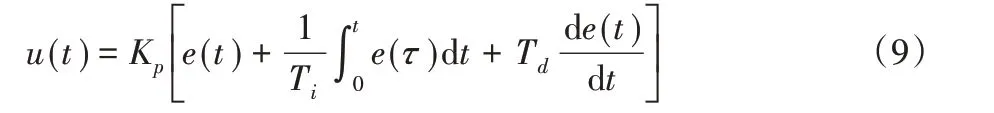
其中:u(t)为系统的输出，e(t)为系统输入与输出的误差。并由比例增益系数Kp，积分时间Ti，微分时间常数Td组成控制器的参数。为方便分析和计算，将式（9）替换为如下形式:

其中有Ki=Kp/Ti，Kd=KpTd。Ki为积分增益系数，Kd为微分增益系数。

动态性能指标有上升时间、调节时间、峰值时间、超调量、稳态误差等，但这些指标相互矛盾，无法同时满足。为评价系统优化过程中的性能，需要选择另一类型的性能指标进行评价。常见的性能指标有时间绝对偏差积分（Integral Time Absolute Error，ITAE）、绝 对 误 差 积 分（ Integral Absolute Error，IAE）、时间误差平方积分（Integral Time Square Error，ITSE）、平方误差积分（Integral Square Error，ISE）等。

改进后的IMO-BBO算法PID参数优化目标是在给定的寻优控件中，寻找到一组适宜的Kp、Ki、Kd，使得系统的性能指标达到最好。本文选用ITAE 作为评价PID 算法性能的指标，表达式如式（11）所示:

4 仿真实验

实验中采用表1 中的13 个基准测试函数进行测试，测试函数在可分解性、多峰、作用域等性质上各有不同。实验所用计算机配置为:Intel i5-3210M，2.5 GHz 双核处理器，Windows 7操作系统，所有算法均采用Matlab 2015b实现。

其中，函数f6、f8、f10、f11、f12、f13都是单峰函数，在搜索作用域中有且仅有一个局部极小值。函数f1、f2、f3、f4、f5、f7、f9是多峰函数，在进行搜索的作用域中有大量局部极小值。其中，f1、f3、f7的局部最优点数量与函数维数呈正相关，为指数关系增长。大量的局部极小值会使寻优难度增大。

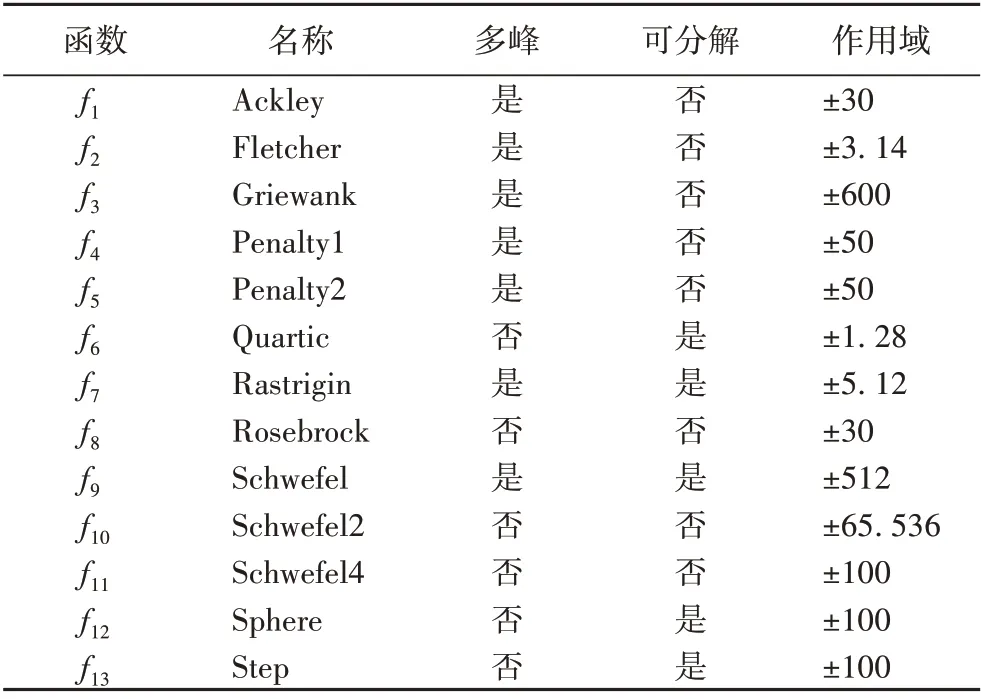
表1 基本测试函数特性Tab. 1 Features of benchmark functions

4.1 IMO-BBO中改进算子贡献度分析

为分析本文中引入的改进迁移算子和双种群策略算子对原BBO 算法的贡献程度，对这两个算子进行实验验证。这里将基于改进迁移算子的BBO 算法简称为“模型1”，将基于双种群策略算子的BBO算法简称为“模型2”。

BBO 算法部分的初始化参数设置一致:栖息地数量为50，迭代的最大次数均为50次，个体变异率为0.05，最大迁入率和最大迁出率均为1。其中，模型2的交叉概率为0.1，交叉因子为0.3。选用蒙特卡罗方法对以上问题进行模拟实验，分别进行50轮实验，得到的结果如表2所示。

表2 是对不同维度、不同性质的测试函数、不同优化算法进行实验所得到的最小HSI 结果，HSI 越小表示寻优结果越佳。表中d= 1 表示测试函数为一维函数，d= 20 为维数为20的高维函数。

表2 不同测试条件下的寻优结果Tab. 2 Optimization results under different test conditions

从表2 中可以看出:在对低维的一维函数进行最小值寻优时，相比于BBO 算法，模型1 和模型2 不论是在单峰和多峰函数上都表现出了很强的搜索能力，在函数f2和f9上找到了更优的解；在对维数为20 的高维函数进行测试时，13 个测试函数中，有11 个得到的结果比BBO 算法更好。因为模型1 中的改进算子通过差分进化策略生成新的个体，使最优解的局部勘探能力得到了加强，模型2 中的协作算子通过种群间的信息交互，丰富了种群的多样性，使其具有更强的全局搜索能力。

4.2 IMO-BBO与其他算法的对比

为评估改进后IMO-BBO 算法在最优解搜索能力、最优解精度、动态稳定性，将本文提出的IMO-BBO 算法与基于协方差迁移算子和混合差分策略的BBO（Covariance Matrix based Migration BBO hybrid with Differential Evolution，CMM-DE/BBO）算法［23］和BBO 算法进行比较。BBO 算法部分的初始化参数与上文一致。其中，IMO-BBO 算法的交叉概率为0.1，交叉因子为0.3。

选用蒙特卡罗方法对以上问题进行模拟实验，且分别用不同的优化算法对表1 中的13 个测试函数进行50 轮实验，得到的结果如表3所示。其中，表3是各算法对不同维度和不同测试函数进行优化后得到的最小HSI 值和平均HSI 值，表中对适应度值更小的结果进行加粗。

由表3 中得到的最小HSI 值部分看出:在函数维度为1时，相比于其他算法，改进后的IMO-BBO 算法在单峰函数和多峰函数的测试中对最优解有更强搜索能力，且在多峰函数f2，f9上得到了更小的HSI；在函数维数为20 时，IMO-BBO 算法在12 个测试函数上得到了比其他算法更好的结果。说明IMO-BBO 算法有寻优能力更强、收敛精度更高的特点，在问题求解精度方面有了更有效的提高。同时在数值优化方面，该算法是一种行之有效参数寻优算法。

同时，因IMO-BBO 算法需对迁移距离、双种群的寻优以及种群间的协作进行计算，总的时间复杂度相比BBO 算法更高，这与改进算法对局部和全局寻优能力进行平衡有关。为评价IMO-BBO 算法的稳定性，避免单次优化结果不准确，将几种算法分别进行了50 次蒙特卡罗实验，并分别记录了各算法每次运行结束后的HSI 值，得到表3 中各算法的平均HSI。可以看出，在低维函数和高维函数的寻优能力上，CMM-DE/BBO算法与IMO-BBO算法实力相当，但IMO-BBO算法在更多的测试函数中表现更佳，经50 次模拟实验得到了HSI 最优的结果最多，在寻优能力上具有更优良的性能。总的来说，IMO-BBO 算法在大部分的测试函数中有更理想的结果，同时能保证较稳定的全局寻优能力。

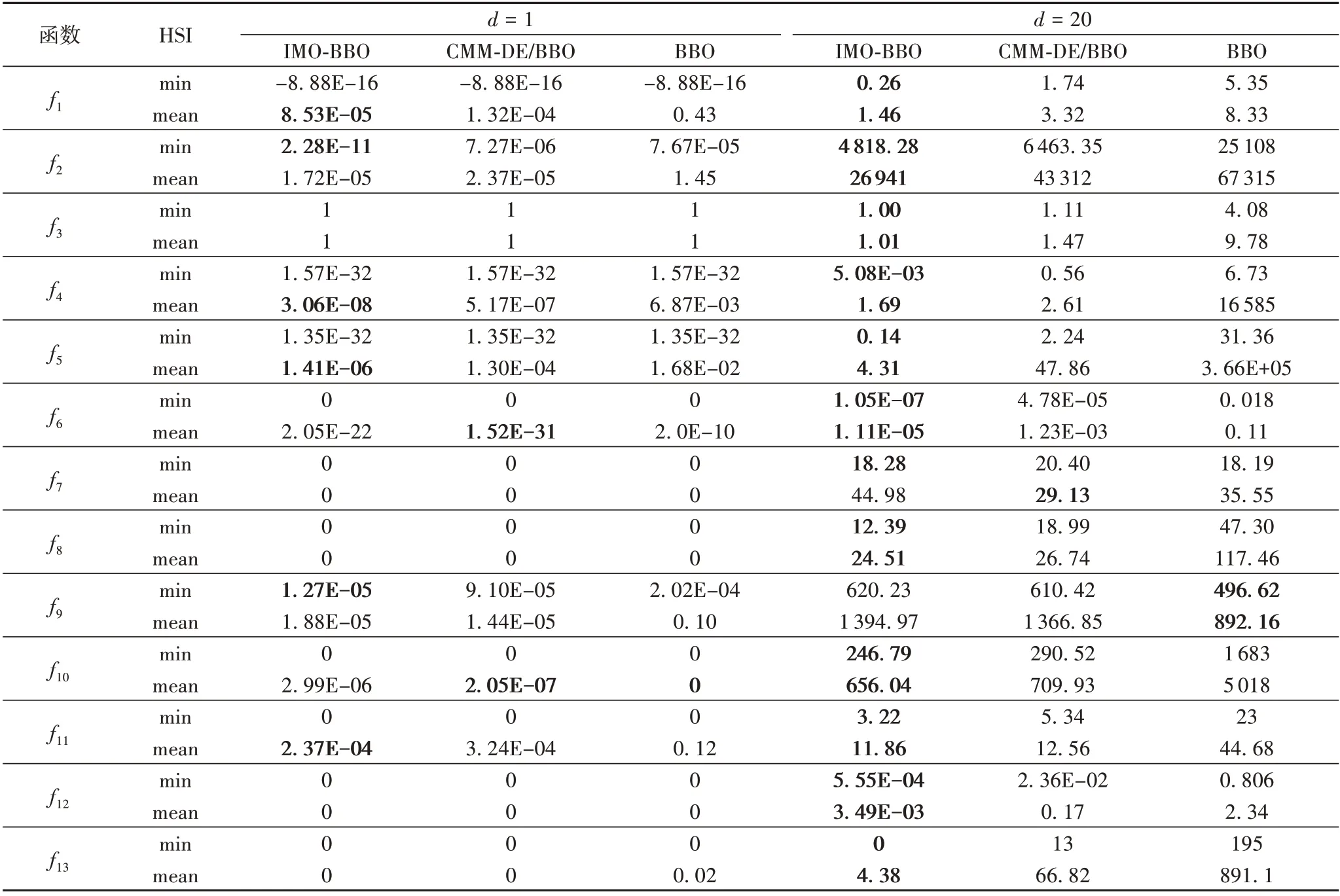
表3 蒙特卡罗寻优HSI最小值与平均值Tab. 3 Minimum and average HSI values of Monte Carlo optimization

图3 分别展示了IMO-BBO 算法、CMM-DE/BBO 算法和BBO 算法（以下简称为“3 种BBO 算法”）对Sphere 函数寻找函数极小值时HSI 随迭代次数的变化情况。其中，上文模拟实验使用的初始化参数，依旧作为3 种BBO 算法的初始化参数。

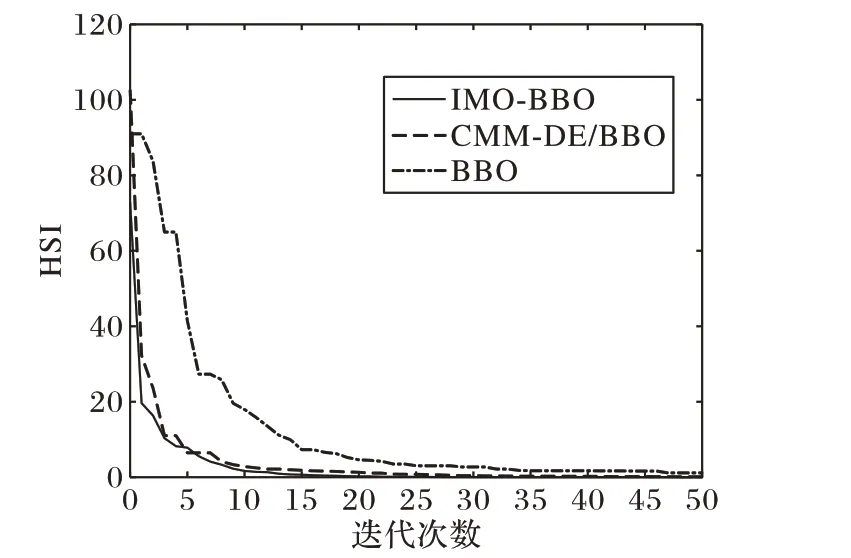
图3 三种BBO算法在Shpere函数中寻优情况Fig. 3 Optimization results on Sphere function of three BBO algorithms

从图3 的三种BBO 算法优化Sphere 函数的HSI 变化情况可以看出，在前15 次迭代中，3 种BBO 算法收敛速度相当，其中IMO-BBO 算法的收敛速度更快。图4 中包含了从第25 次至50 次迭代放大后的HSI变化情况，可以看出IMO-BBO 算法相较于其他2种算法得到的HSI值更小。

由上述结果可知，相比于其他两种寻优算法，改进后的IMO-BBO 算法具有更好的最优值搜索能力。主要在于对算法做了以下改进:1）对迁移操作的改进，使算法能在最优解附近做进一步搜索，提升了局部搜索能力。2）双种群独立进化后，使用协作算子产生新解，使得算法的全局搜索范围加大，增强了算法对最优解的探索能力。

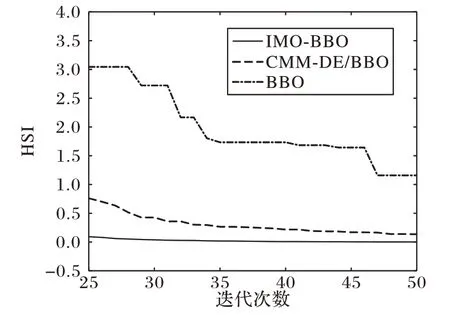
图4 三种BBO算法在Sphere函数中寻优情况（放大）Fig. 4 Optimization result of Sphere with three BBO algorithms（magnified）

4.3 PID控制器参数整定测试

为表明改进的IMO-BBO 算法在全局最优能力和搜索稳定性的特性，本文将算法应用于PID 参数的整定。选择的被控对象为直流电机，被控对象的数学模型如下所示:

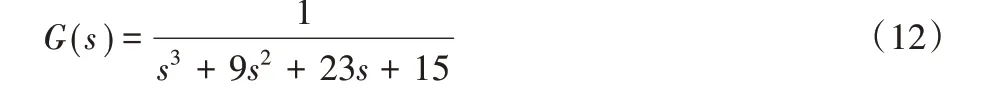
选用IMO-BBO 算法、CMM-DE/BBO 算法、BBO 算法进行比较，算法的适应度指标HSI如式（11）所示。其中，种群数量为50，变异率为0.05，最大迭代次数为50 次。图5 是两种方法寻优过程中适应度指标函数。

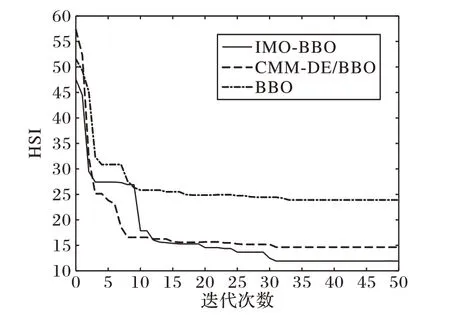
图5 PID优化过程中的适应度变化曲线Fig. 5 Fitness change curve of PID optimization process

图5 是PID 参数优化过程中HSI 变化情况。PID 整定后的阶跃响应曲线如图6 所示。从中可以看出，另外两种BBO算法和原BBO 算法相比，收敛速度更快。从图6 和表4 可以看出，同样经过50 次迭代，本文提出的IMO-BBO 算法确实能得到更好的可行解。

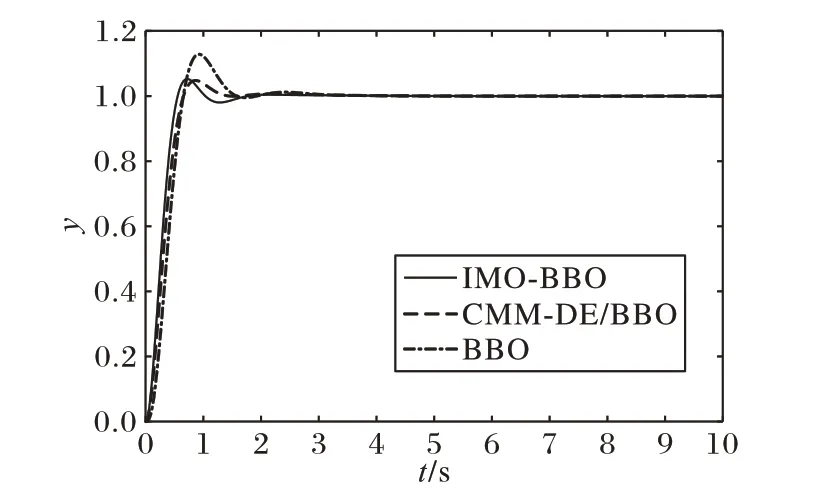
图6 优化后的PID阶跃响应曲线Fig. 6 Optimized PID step response curve

由图5 看出优化过程中，适应度指标HSI 更小时，获得的PID 控制器控制效果更佳。同时，IMO-BBO 使得PID 控制的动态性能指标得到了改善，特别是ITAE 和适应度指标函数，虽然超调量稍微比CMM-DE/BBO 算法大，但上升时间和调节时间更小。

表4 不同算法在参数整定的系统动态响应性能Tab. 4 System dynamic response performance of different algorithms in PID parameter tuning

5 结语

本文针对BBO 算法在迭代后期搜索动力不足、收敛精度不高的问题，提出了一种改进迁移算子的生物地理学算法。结合“优胜劣汰”的进化思想，通过模拟自然环境因素对物种迁移过程的影响，对不适宜迁移的个体进行选择性的替换。并引入多种群概念，在保证两个种群并行独立进化的同时，通过协作算子令两个种群间产生信息交互，使改进后的算法有更高的求解精度和更快的收敛速度。为验证新算法的寻优能力，用13 个常用基准测试函数，在单峰、多峰、高维情况下分别与BBO、CMM-DE/BBO 算法进行了比较，数值实验结果表明，在收敛速度以及对最优解的搜寻能力上，本文所提出的IMO-BBO 算法在测试函数上的表现优于其他几种算法。将改进后的IMO-BBO 算法用于PID 控制器参数整定，得到整定后的PID 参数，仿真结果表明该方法优化后的控制器能有更好的控制性能，也进一步验证了改进后IMO-BBO 算法的优越性能。