H 型钢万能轧机辊缝调整HGC 缸设计与分析

◎窦丽娟 李爱臣

一、前言

在H 型钢轧制时，腹板厚度精度由上、下水平辊压下液压缸完成；翼缘厚度精度由传动侧及操作侧立辊液压缸完成。水平辊缝、立辊辊缝采用HGC 液压缸，伺服阀闭环控制，具有响应快和精度高的特点。

二、HGC 缸的设计与分析

HGC 缸作为万能轧机辊缝调整的重要部件，应根据最大轧制力进行设计，强度分析及校核过程中也要保证测试压力下的安全性。

1.HGC 缸的设计与计算。

HGC 液压缸的主要参数有柱塞直径D0、杆径dr和行程S，参数D0由轧制力P和液压系统工作点的压力Pw决定，按下式计算：

κ——考虑流体系统稳定性的系数，1.3～1.6；

P1—作用在HGC 缸上的轧制力，其为轧制力的一般，，kN；

Pw—工作压力，MPa；

液压缸行程S 要综合考虑油柱高度对轧机刚度和响应频率的影响，不足行程需要在轴承座上设置调整垫板来补偿。

水平压下及立辊压下缸设计时应考虑位移传感器内置、柱塞止转措施、承压垫板等结构设计。此外立辊压下缸还应考虑水平辊压靠时主传动万向接轴的影响。

（1）HGC 缸壁厚度设计与计算。

缸体壁厚按以下工程计算方法进行。

式中δ—缸体壁厚，mm；

Pmax—试验压力，Mpa；

[σ2]—许用应力，MPa；其按下式确定。

σb—缸体材料抗拉强度，Mpa；

n—安全系数，根据工程实践取值。（2）HGC 缸缸底厚度设计与计算。

缸底厚度按以下工程计算方法进行。

式中h—缸底厚度，mm；

2.HGC 缸密封。

密封是液压缸非常重要的组件，它的可靠性直接影响液压缸是否能稳定工作。如图1 所示，柱塞与缸盖结合处，活塞与缸体结合处均采用组合密封。如图4，组合密封由主密封及辅密封O 形圈组成，通过径向过盈配合及O 型圈的预压缩，可以提供有效预紧力，保证在低压及高压工况下都能使密封紧密贴合在密封面上，具有良好的密封特性。密封圈的材料主要由PTEE（聚四氟乙烯）组成，具有良好的耐高温，耐磨性。

防尘圈采用带有双O 形圈提供预紧力双唇防尘圈，可有效地防止灰尘和污垢进入系统，副密封唇口和带有O 形圈的密封串联组合使用可有效减少残余油膜。导向带则可以有效吸收活塞运动时的偏载力，有效保护密封。

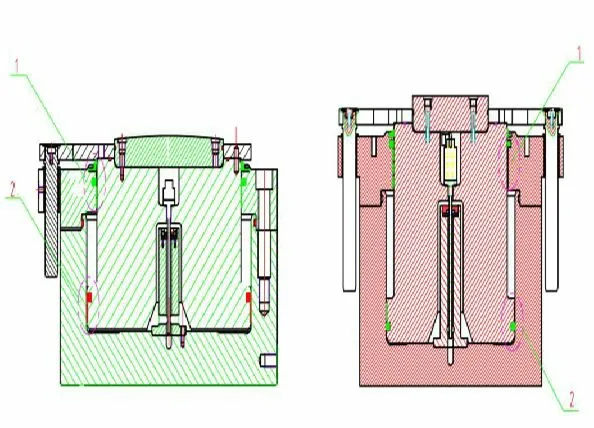
图1 辊缝调整HGC 缸密封示意图

图2 组合密封圈示意图

3.HGC 缸体的分析。

完成初步的设计计算后应采用有限元方法对缸体进行分析、校核，从而对缸体细节进行优化。

在HGC 缸柱塞完全伸出状态进行分析，试验压力32Mpa。将缸体上的油孔、螺孔等进行简化处理以便网格划分。取缸体模型的1/2 为对象进行分析。

在对缸体进行有限元分析时基于在载荷作用下不会发生超出材料屈服限的塑性变形的假设。

缸体材料选择调质处理的42CrMo，材料性能及许用应力如下表：

?

（1）水平辊辊缝调整HGC 缸缸体分析。

缸体有限元模型见图3。

图3 水平辊辊缝调整HGC 缸缸体有限元模型

模型的具体边界条件- 约束方式见图5，分别施加对称约束、竖直方向的固定约束。模型的具体边界条件-加载方式见图4。

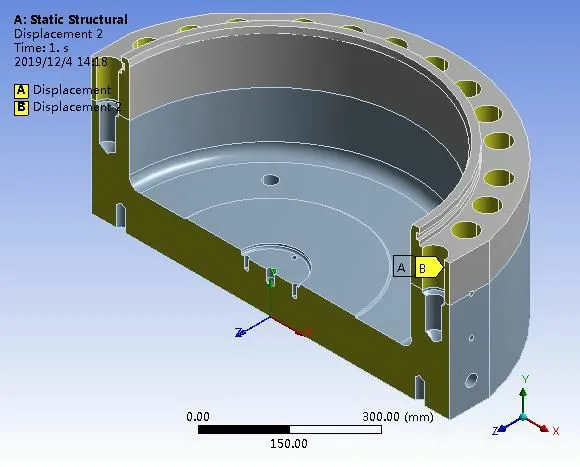
图4 水平辊辊缝调整HGC 缸缸体模型边界条件—约束

图5 水平辊辊缝调整HGC 缸缸体模型边界条件—载荷

水平辊辊缝调整HGC 缸缸体的von-mises 应力分布云图（见图5）。最大应力为536.23MPa，位置在缸体内部的圆弧环面上，为应力集中区，详见云图的红色区域；其余部分的应力均小于480MPa。

图6 水平辊辊缝调整HGC 缸缸体等效应力云图

（2）立辊辊缝调整HGC 缸缸体分析缸体有限元模型见图6。

图7 立辊辊缝调整HGC 缸缸体有限元模型

模型的具体边界条件-约束方式见图7，分别施加对称约束、竖直方向的固定约束。模型的具体边界条件-加载方式见图8。

图8 立辊辊缝调整HGC 缸缸体模型边界条件—约束

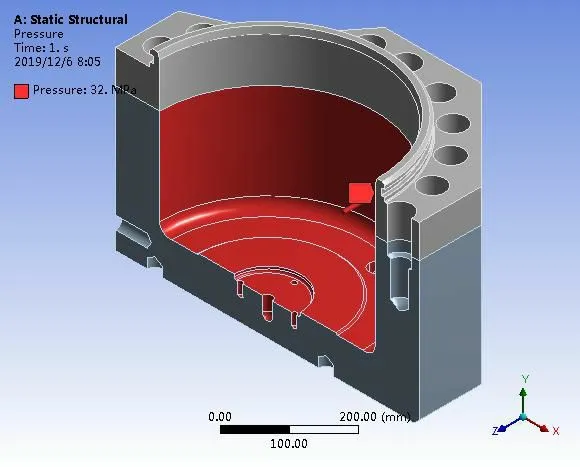
图8 立辊辊缝调整HGC 缸缸体模型边界条件—载荷

立辊辊缝调整HGC 缸缸体的von-mises 应力分布云图（见图8）。最大应力为433.65MPa，位置在缸体内部的圆弧环面上，为应力集中区，详见云图的红色区域；其余部分的应力均小于340MPa。

图9 立辊辊缝调整HGC 缸缸体等效应力云图

HGC 缸缸体的最大应力均低于材料的曲服强度，通过与实际运行的生产线中应用的HGC 缸对比，该结果满足生产需要。

三、结语

HGC 缸作为万能轧机辊缝调整的关键部件，设计过程中的计算校核非常重要。本文通过对多个H 型钢轧钢生产线的调研、分析，对HGC 缸进行设计计算并分析校核，为以后的设计和研究工作提供参考和依据。