煤矿井下随钻测斜仪误差联合校正方法

乔美英，王 波，肖学军，许城宽，闫书豪

煤矿井下随钻测斜仪误差联合校正方法

乔美英1，王 波1，肖学军2，许城宽1，闫书豪1

(1. 河南理工大学 电气工程与自动化学院，河南 焦作 454000；2. 河北省煤田地质局第四地质队，河北 张家口 075100)

为降低煤矿井下随钻测斜仪随钻测量钻孔姿态角参数的误差，建立基于递推最小二乘的误差补偿数学模型，采用椭球拟合法、点积不变法和旋转平面拟合法的联合校正方法对随钻测斜仪进行误差补偿校正。对研发的随钻测斜仪进行数值仿真和双轴转台实验，用联合校正方法对实验数据进行误差补偿校正，校正前俯仰角和方位角的最大绝对误差分别为4.7°和5.1°，校正后为0.8°和0.9°，校正后测量精度满足随钻测斜仪要求。实验结果表明，该方法可以对煤矿井下随钻测斜仪进行有效的误差补偿校正。

煤矿井下随钻测斜仪；联合校正；误差补偿校正；俯仰角；方位角

煤矿井下钻探技术在采集地层、构造、水文地质资料等地质钻孔以及探放水、抽采瓦斯等措施钻孔中有着广泛的应用。为检验钻孔轴迹，一定比例的钻孔在钻进时配备随钻测斜仪实时测量钻孔的姿态角等参数，以掌握钻孔轴迹，但是随钻测斜仪姿态测量模块中的传感器由于工艺及安装技术等问题，导致测量姿态角参数存在误差，无法精确地测绘钻孔轴迹。

随钻测斜仪姿态测量模块由三轴加速度计和三轴磁强计传感器组合而成[1]，为了获得精确的钻孔测量参数，必须要对传感器进行数据校正。研究传感器校正方法较多，郝东等[2]采用赫姆霍兹线圈校正磁强计，代刚[3]采用离心机校正加速度计，这两种方法的校正精度高，而且建模简单，但是需要提供高精度的仪器，实验环境也难以提供。郭卫等[4]建立基于BP神经网络模型的方法校正加速度计；晁正正等[5]采用模拟退火、宋忠国等[6]采用粒子群优化方法校正磁强计，通过训练优化迭代得到校正需要的最优拟合值，但训练需要大量数据而且难免出现泛化能力不足；陆欣等[7]采用最大似然校正法校正加速度计；龙礼等[8]采用自适应校正方法校正磁强计，通过建立复杂数学模型可以校正加速度计或磁强计，但稍显复杂。上述方法多难以应用在随钻测斜仪工程实际中，并且多是对单一传感器校正，随钻测斜仪姿态测量模块需要考虑多传感器之间校正对准问题、传感器坐标系与载体坐标系的校正对准等问题。

在以上研究的基础上，根据加速度计和磁强计误差建立的测量模型，首先采用椭球拟合法校正加速度计，然后采用点积不变法校正磁强计以及传感器之间的未对准误差，最后采用旋转平面法校正传感器与载体坐标系的未对准误差，并通过对研发的随钻测斜仪进行实验来验证该方法的有效性。

1 随钻测斜仪随钻测量原理

煤矿井下随钻测斜仪姿态测量模块由三轴加速度计和三轴磁强计组成，其原理如图1所示。

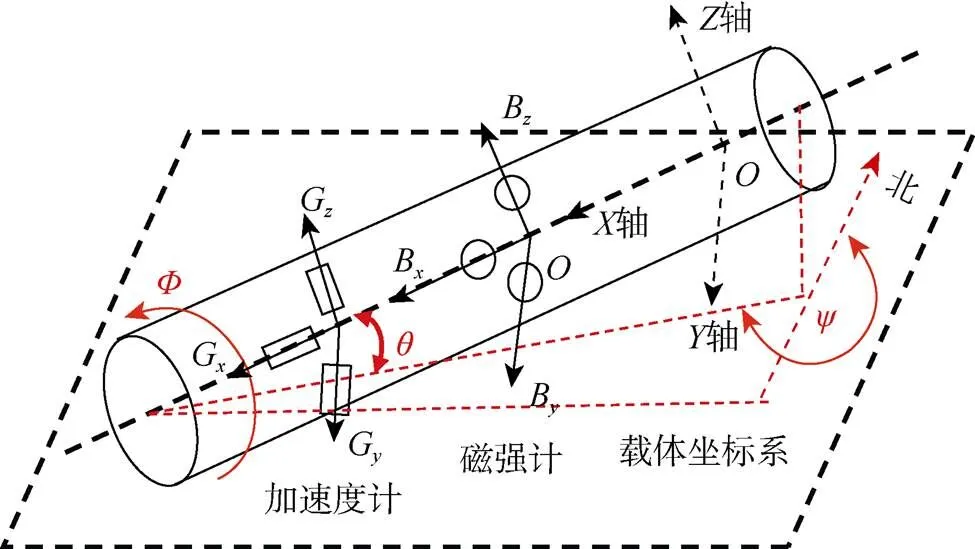
图1 姿态测量原理示意图

在钻孔作业时，加速度计实时测量地球的重力场分量G、G、G，磁强计实时测量地球的磁场分量B、B、B。测量值经过数值转换根据式(1)计算出俯仰角，工具面角和方位角，可以确定钻孔的实时姿态[9-10](其中0为重力矢量和)。

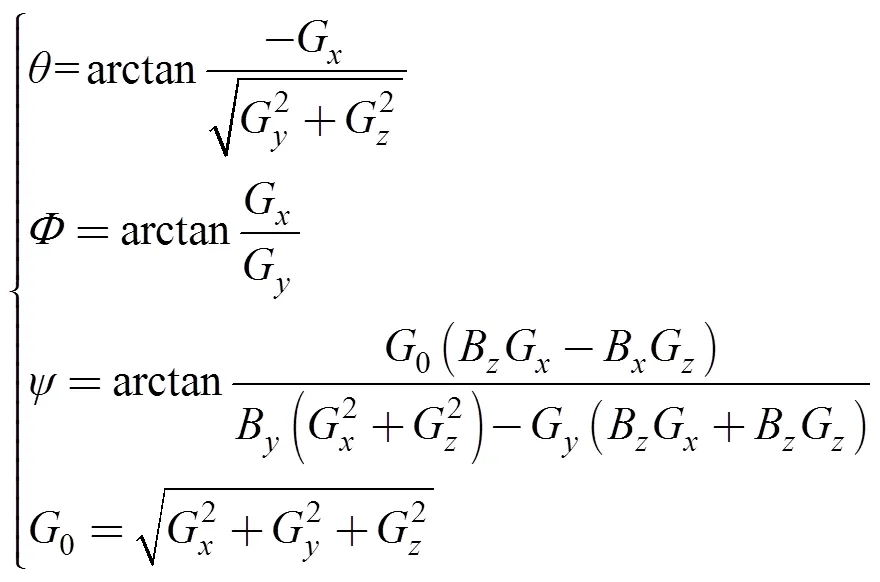
2 加速度计的单独校正

随钻测斜仪中的磁强计容易受到周围环境磁干扰，测量数据不精确，校正后的结果对第二步的点积不变法产生影响，因此，第一步选择单独校正加速度计。

2.1 加速度计误差校正模型

加速度计由于工艺及安装技术等的影响存在各种误差[11]。根据文献[4,7,12]得到加速度计测量模型：

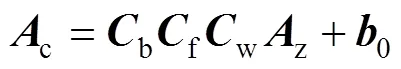
式中：c为加速度计测量值；z为加速度计真实值；b为比例系数误差；f为非正交误差；w为未对准误差；0为零位偏差。

引入可逆矩阵=bfw和=–1并代入式(2)，整理得到加速度计误差补偿校正模型：

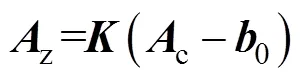
2.2 误差补偿校正与椭球拟合模型的转换

理想情况下，加速度计以任意姿态旋转，稳定下加速度计测量重力矢量不变，输出轨迹是一个正球体，但是受误差影响轨迹会畸变为椭球。

对加速度真实值z求模的平方：

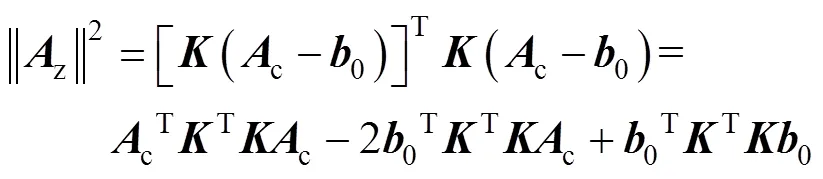
式(4)整理为椭球标准式：

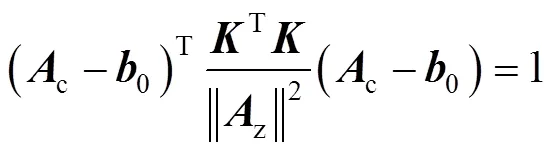
椭球的一般式为：

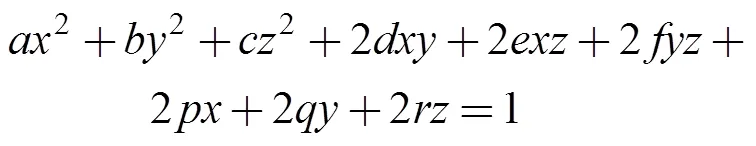
式(6)整理为椭球矩阵式：

根据式(7)可以得到：

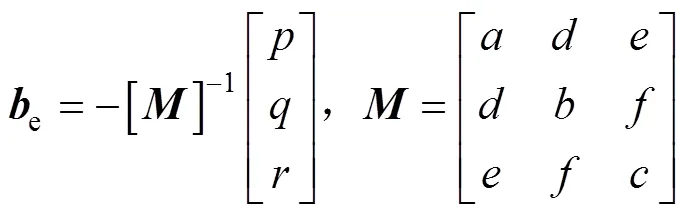
—，—是椭球的系数，其中0表示球心。根据式(5)、式(7)、式(8)得到：

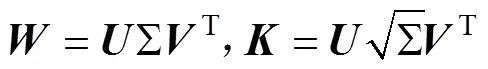
将式(10)代入式(3)，加速度计误差补偿校正模型可以表示为：

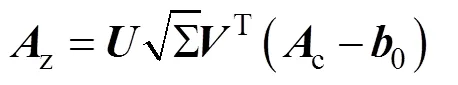
加速度计校正，关键是拟合出椭球系数。

2.3 基于递推最小二乘的椭球系数

递推最小二乘算法是一种在线算法，利用原有参数进行下一步估计，可以做到运算量小，实时进行估计，逐步得到最优解，而且递推过程不需要批量处理，随着迭代次数的增加估计精度也越来越高[13-14]。

根据2.2节可知加速度计校正模型可以用椭球模型来表示。

带有噪声的椭球方程为：

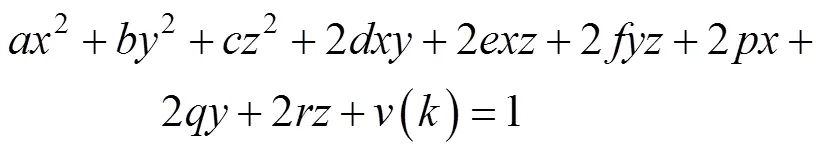
式中：()为噪声；、、为加速度计测量分量。椭球系数定义为：

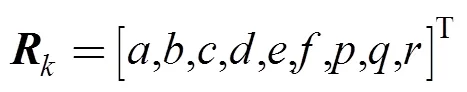
加速度计的实时测量数据为[,,]T，按照椭球参数可定义：

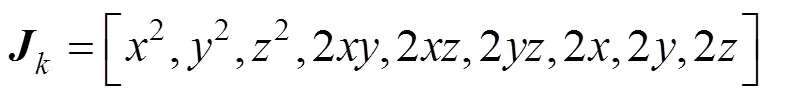
由式(12)—式(14)得到递推最小二乘式：

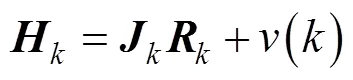
根据式(16)递推拟合椭球系数，其中，各项的初值设为0，初值设为106(为单位矩阵)，设为常值1。

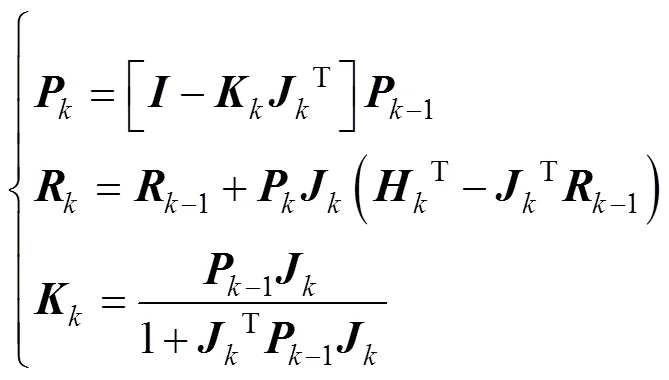
3 加速度计和磁强计之间的相互校正

采用点积不变法校正磁强计，校正过程中加速度计和磁强计之间的未对准误差也可以消除[15-16]。点积不变法是利用了相对位置不变的两条矢量数量积为常数的性质。假设地磁矢量是大小和方向都不变的常数矢量，重力矢量与地磁矢量在任意姿态下的点积都为常数(const)。设重力矢量为z，地磁矢量为z，矢量公式为：

以上研究为基层国家机关“谁执法谁普法”责任制的建立和实施提供了理论依据，对法律在全社会的普及大有裨益。

根据文献[5-6,8,16]得到磁强计测量模型：

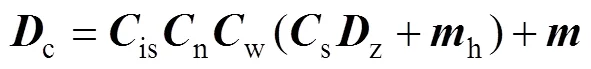
式中：c为磁强计测量值；z为磁强计真实值；is为比例系数误差；n为非正交误差；w为未对准误差；s为软铁误差；h为硬铁误差；为零位偏差。引入=isnws、0=isnwh+(0为总偏差)和m=–1代入式(18)整理得：

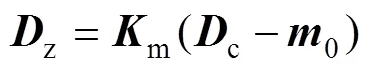
将z和式(19)代入矢量公式(17)得：

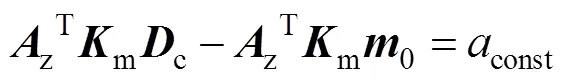
定义m=，m0=代入式(20)得：

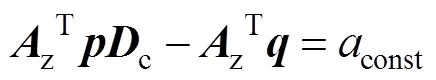
式中：zT为经过校正的加速度计真实值；c为磁强计测量值。多次测量建立超定方程组，利用递推最小二乘拟合得到和的值，代入m=，m0=计算得到磁强计的误差补偿矩阵m和总偏差0。

4 传感器与载体坐标系的未对准误差校正

椭球拟合法不能校正传感器坐标系与载体坐标系之间的未对准误差[17]。这里引入坐标系旋转理论，未对准误差可以看作传感器坐标系()与载体坐标系()之间的多次旋转，假设两个坐标系之间的未对准角度为、、，按、、顺序旋转，旋转矩阵由式(22)来表示[11]：

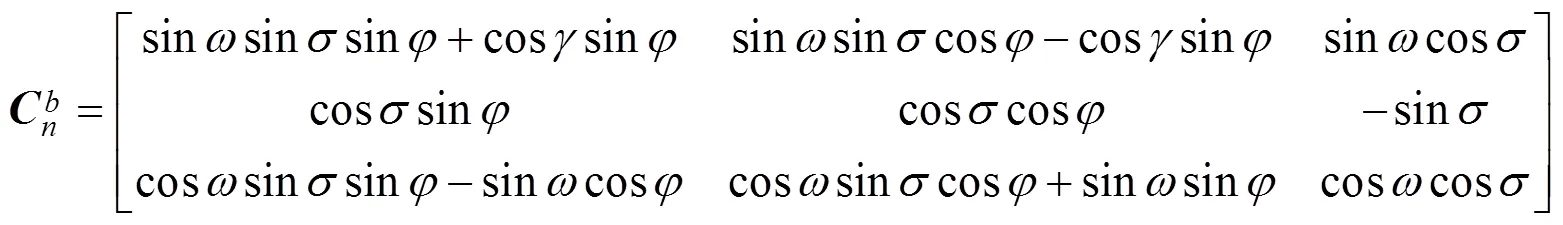
旋转平面拟合，是指在均匀的矢量场中，在固定的位置下，传感器绕任意轴旋转时，在旋转轴输出是一个常数，另外两轴的输出矢量将会形成一个圆环平面[18]。假设A、A、A是加速度计经过椭球拟合校正后的值，同时引入：

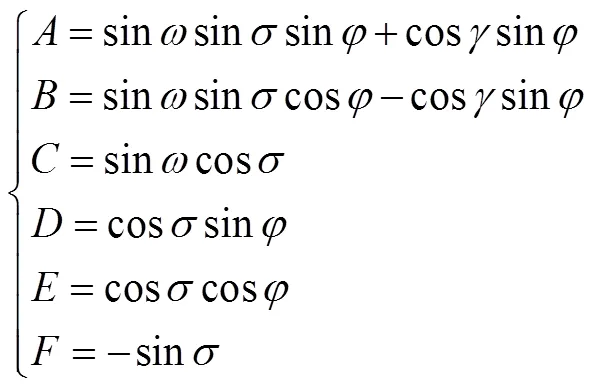
当绕轴转动，在载体坐标轴输出为常数。

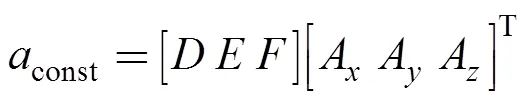
式(24)、式(25)为两个空间平面方程，按照++=1代入椭球拟合校正后的值建立超定方程组，求出、、和、、，代入式(23)计算出未对准小角度；代入式(22)计算出结果并用w表示，代入式(3)、式(19)求出加速度计误差补偿矩阵w–1，磁强计误差补偿矩阵w–1m。

5 实验验证

实验分为数值仿真和双轴转台(实测数据)实验。数值仿真是为了验证方法的准确性，双轴转台用于验证方法实际有效性。

5.1 数值仿真

根据式(2)加速度计的测量模型做出如下假设：比例误差设为：b=diag(1.2,1,0.8)；偏差设为：0= [0.1,0.2,0.3]T；三轴非正交误差角设为=1°，=2°，=3°；坐标系未对准误差角设为=2°，=1°，=1.5°；三轴分量设为[0,0,1]T[7]。根据设置的误差参数计算误差补偿矩阵和偏差的参考值。

根据式(18)磁强计的测量模型做出如下假设：比例误差设为：is=diag(1.2,0.8,1)；偏差设为：=[900,860,–780]T；三轴非正交误差角设为=1°，=0.5°，=1°；坐标系未对准误差角设为=1°，=2°，=3°；硬铁误差设为h=[–75,–70,85]T；软铁误差设为s=[1.2,0.2,0.3;0.3,1.4,0.4;0.2,0.4,1.5]；三轴分量设为[0,0,48 152]T[16]，根据设置的误差参数计算误差补偿矩阵和偏差的参考值。

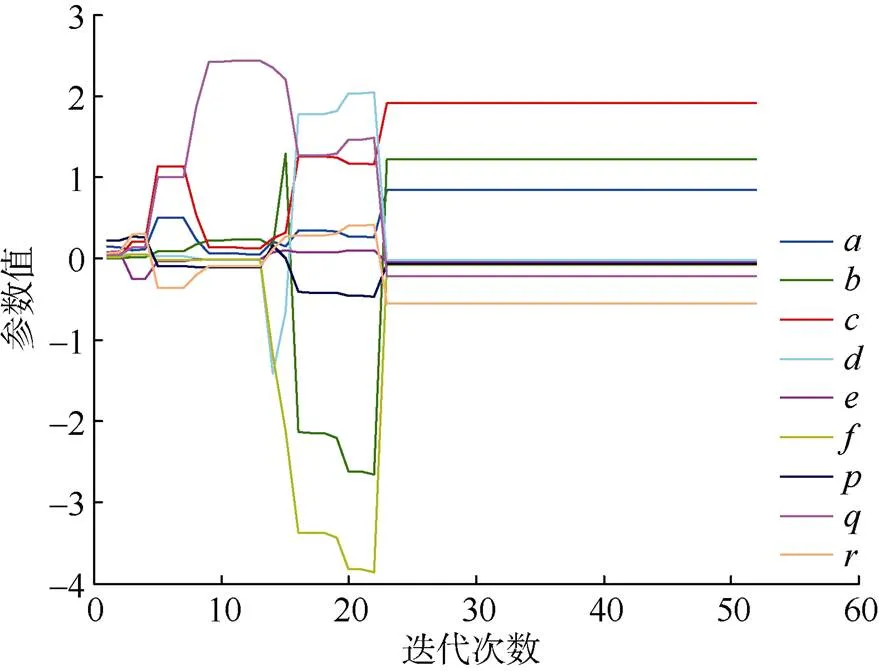
图2 椭球拟合参数估计

假设载体坐标系三轴为东北天指向即轴指向东，轴指向北，轴指向天。根据坐标系旋转理论做旋转运动，旋转角度分别设为绕轴、轴、轴旋转360°，绕轴旋转每次间隔120°，绕轴旋转每次间隔60°，绕轴旋转每次间隔30°，共计216个测点。根据文献[11]中的旋转矩阵公式求出每次旋转后的加速度计和磁强计的三轴分量，作为加速度计和磁强计无误差输出数据，按照上文求出的参考值计算加速度计和磁强计误差输出数据。

将加速度计误差数据代入MATLAB软件编写的递推最小二乘程序，其中设置为106，椭球系数—、—初始值都设置为0，经过24次迭代，参数趋于稳定，迭代输出结果如图2所示，椭球系数=[0.846 2，1.220 1，1.908 0，–0.016 4，–0.040 9，–0.083 4，–0.069 5，–0.217 3，–0.551 8]T。

根据递推的结果计算经椭球拟合的加速度计误差补偿矩阵和偏差；计算经椭球+旋转平面拟合的加速度计误差补偿矩阵和偏差，结果见表1。

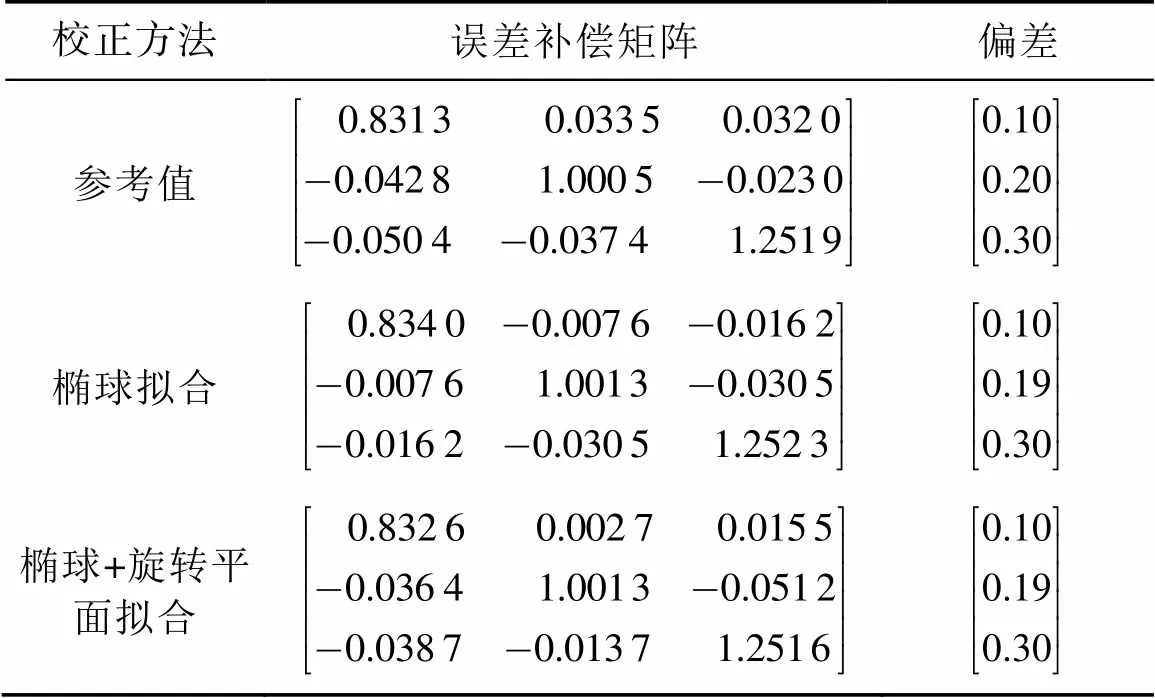
表1 加速度计参考值以及各校正方法结果

将磁强计误差数据按照点积不变法计算磁强计误差补偿矩阵和偏差；计算点积不变法+旋转平面拟合的磁强计误差补偿矩阵和偏差，结果见表2。

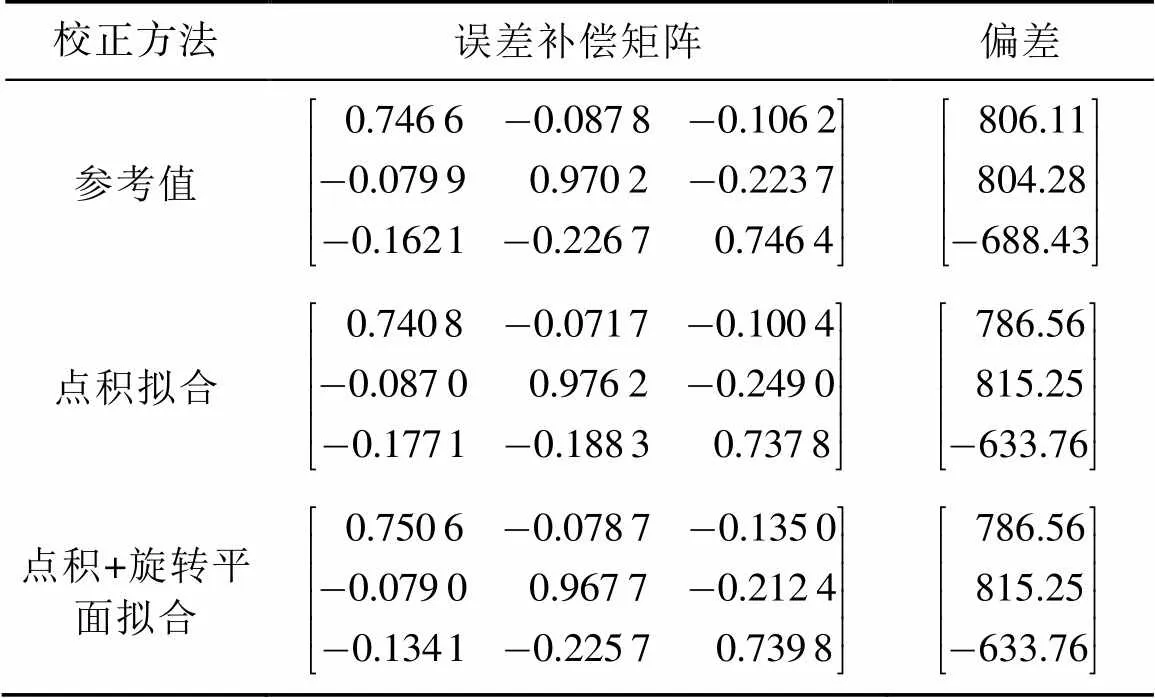
表2 磁强计参考值以及各校正方法结果

MATLAB软件绘制加速度计校正前和经椭球拟合校正后测点空间分布图以及磁强计校正前和经点积不变法校正后测点空间分布图，如图3所示，两者校正前都表现为椭圆，并且分布在球体外，校正后表现为圆形分布在球体表面。

椭球拟合校正后的加速度计与点积校正后磁强计的未对准误差消除，即传感器坐标系对准。将磁强计数值缩小48 152倍(根据设的分量大小缩小，只改变大小，不改变方向)，目的是将两个传感器的坐标系绘制在同一个坐标系。绘制椭球拟合校正后的加速度计与点积法校正后的磁强计测点俯视图，如图4a所示。

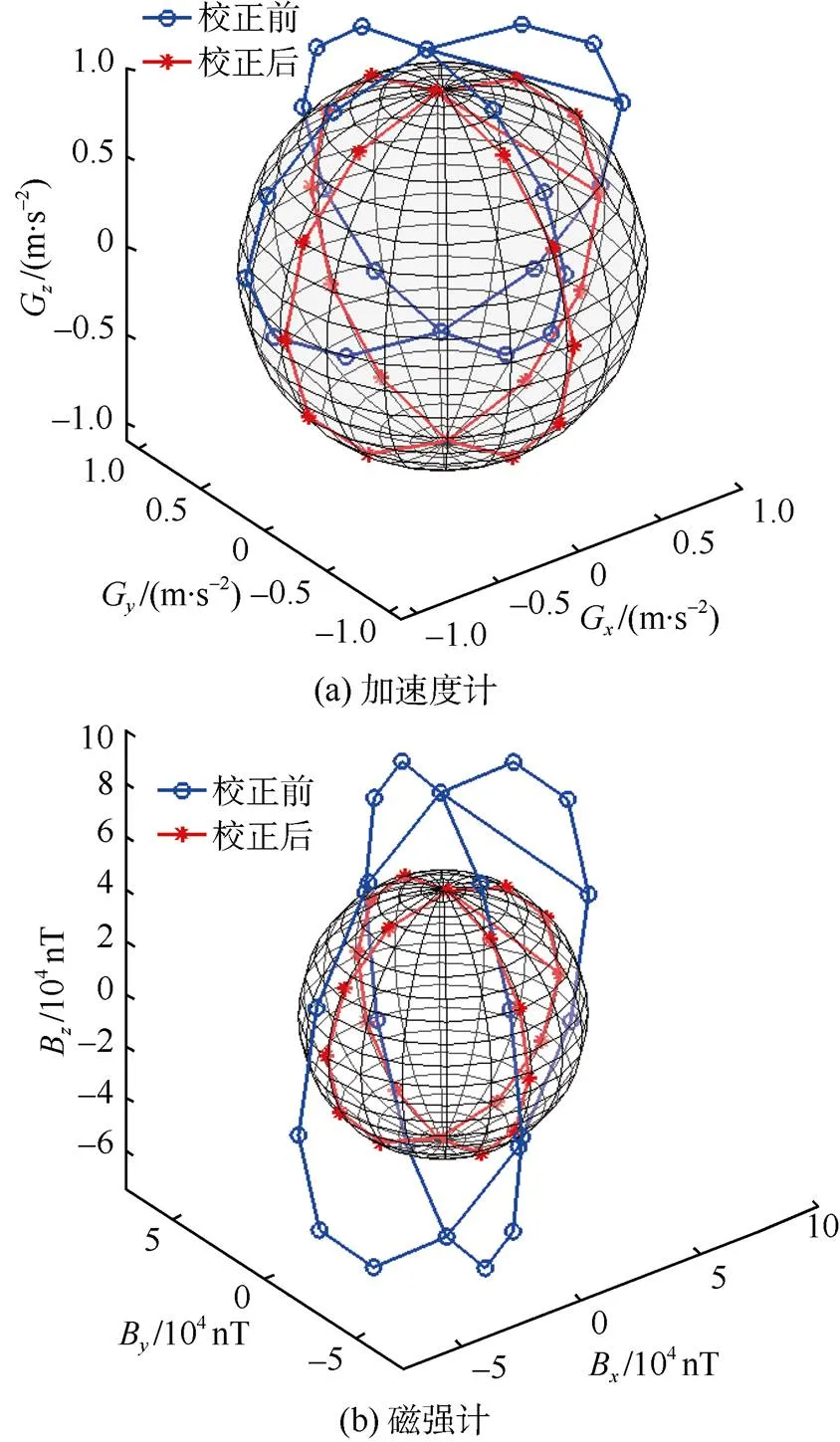
图3 校正前后测点空间分布

经旋转平面拟合的传感器坐标系和载体坐标系未对准误差消除。数值仿真中表现为传感器所在坐标系和载体坐标系坐标轴方向重合，如图4b所示。

5.2 双轴转台实验

为进一步说明方法的有效性，采用自主研发的随钻测斜仪进行实验。该随钻测斜仪主要由单片机(STC15F2k 60S2)、姿态测量单元(MMA8451加速度计和HMC5883L磁强计)、存储器(16兆字节Flash芯片)、时钟(DS1302)和通信接口构成。该主控芯片单片机速度是传统单片机的8~12倍，对传感器数据的采集和处理会更加高效与准确，实验过程中姿态测量模块测量的数据，通过UART协议传输到单片机，并存储到Flash中。

5.2.1 拟合校正参数

将随钻测斜仪用固定板固定在双轴转台上，分别绕、、轴以任意姿态转动若干次，为避免非重力加速度干扰，获取转动结束时静止状态下数据，对每个姿态测量10次，并求均值，共获得100组测量数据(加速度计和磁强计读数)。

表3是利用本文方法求出加速度计和磁强计的校正参数，计算时需要进行数值转换。

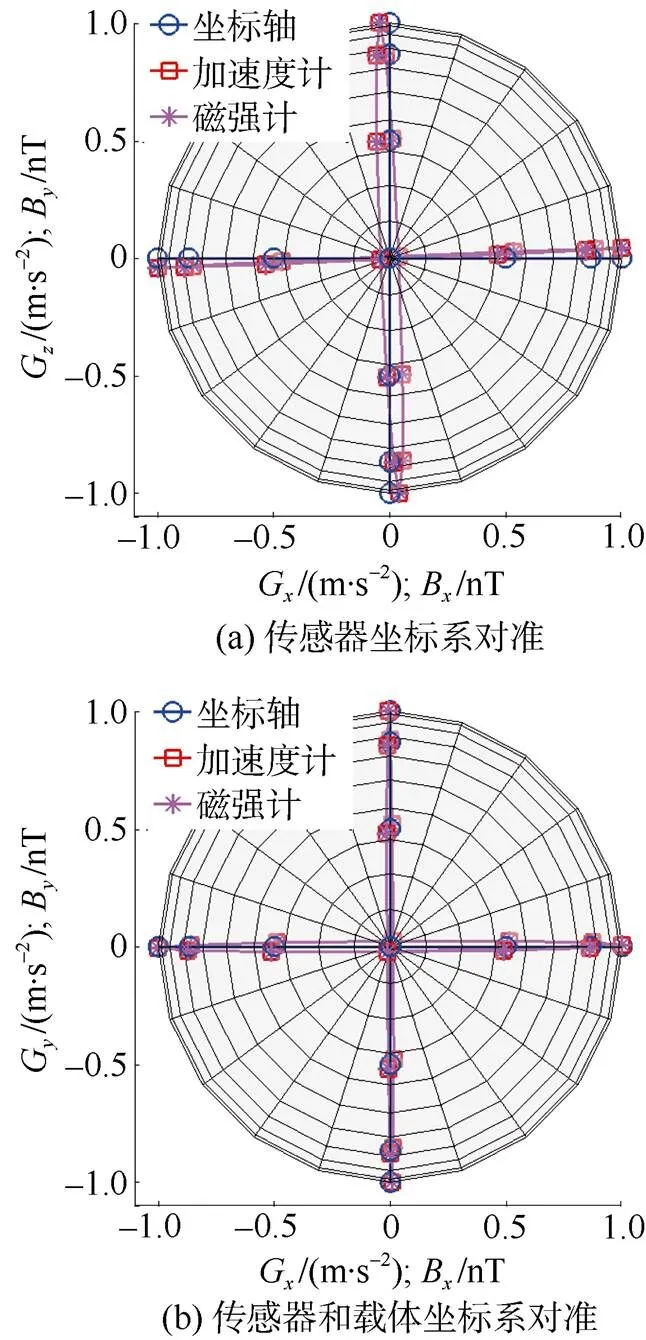
图4 未对准误差校正

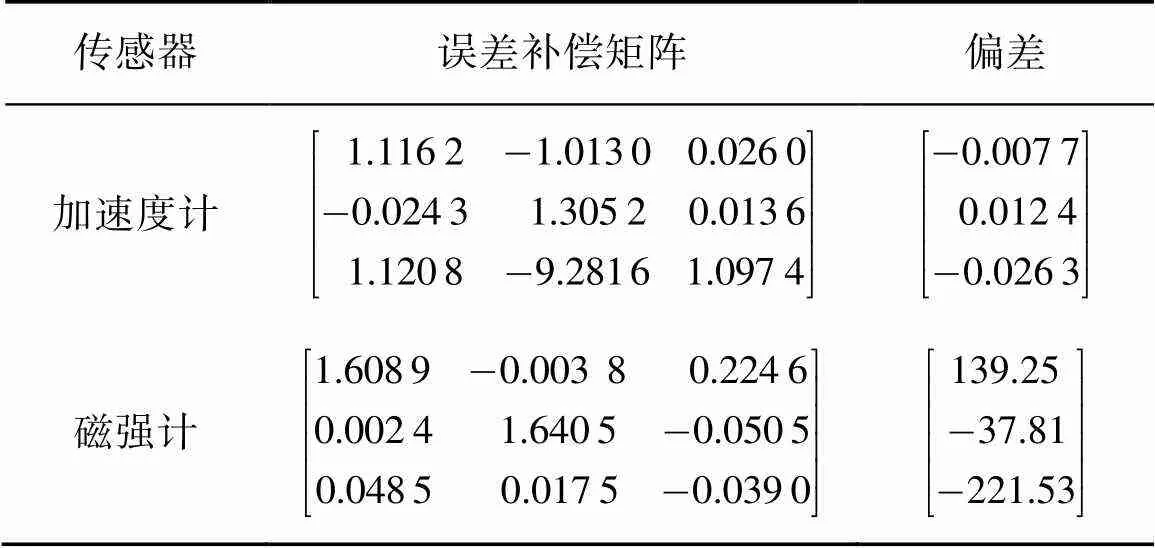
表3 加速度计和磁强计校正参数

5.2.2 姿态角补偿校正

补偿校正最终目的是降低随钻测斜仪测量的姿态角误差，即俯仰角和方位角误差。

a.俯仰角 在双轴转台上固定好自主研发的随钻测斜仪。以水平0°为基准，控制转台以间隔10°顺序上仰到80°，接着回到水平基准再控制转台以间隔10°顺序下俯到–80°，为避免非重力加速度干扰，每次转动结束时在静止状态下采集测量数据并存储在Flash中，每个角度测量10次求均值，最终获得17个测量值。对采集数据按照表3中加速度计参数校正，绘制校正前与校正后的示意图，如图5所示，校正前分布在球体外，表现为椭球，校正后分布在球体表面。

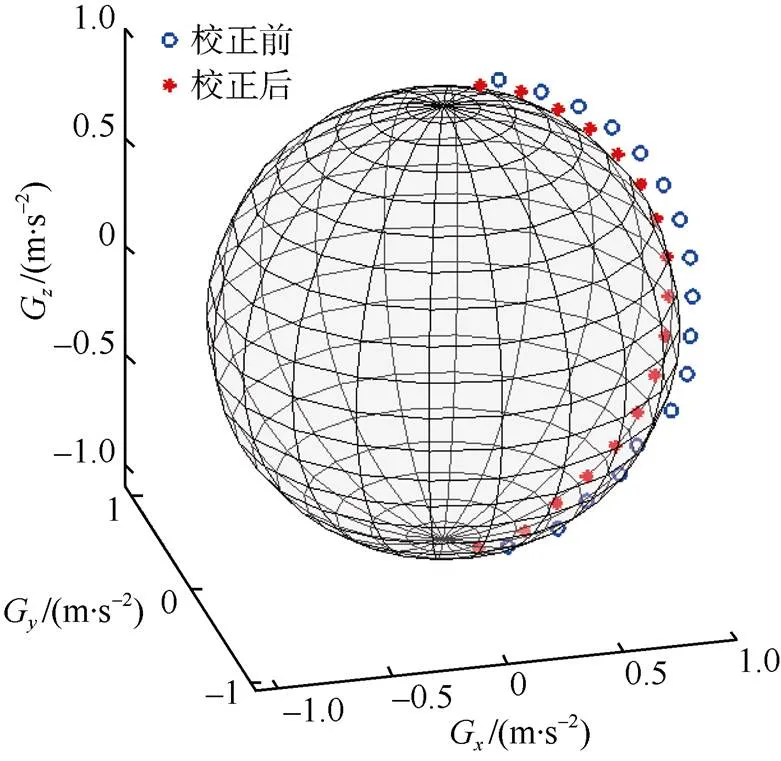
图5 加速度计校正前后示意图

根据式(1)计算校正前和校正后的俯仰角，并分别计算校正前和校正后与参考值(–80∶0∶80)的差。绘制校正前和校正后的俯仰角误差曲线，如图6所示。上仰和下俯的误差最大绝对值分别为3.9°和4.7°，校正后为0.7°和0.8°，校正前后，测量精度提高了一个等级。

图6 俯仰角误差曲线

b.方位角 在同样的实验环境下以水平0°为基准，精密罗盘确定地理北向为0°，将随钻测斜仪指北向0°固定。控制转台以0°为起始隔10°测量，顺时针旋转360°，测量数据存储在Flash中，每个方位角测量10次，求其均值，最终获得36个测量点。对采集数据按照表3中磁强计参数校正，绘制校正前与校正后的示意图，如图7所示，校正前分布在球体外，表现为椭球，偏离球心，校正后分布在球体表面，指向球心。

根据式(1)计算校正前和校正后的方位角，并分别计算校正前和校正后与参考值(0∶10∶350)的差。绘制校正前和校正后的方位角误差曲线如图8所示。校正前，从0°转至180°和180°转至350°之间误差最大绝对值分别为5.1°和4.9°，校正后分别为0.8°和0.9°，校正前后，测量精度提高了一个等级。

图7 磁强计校正前后示意图

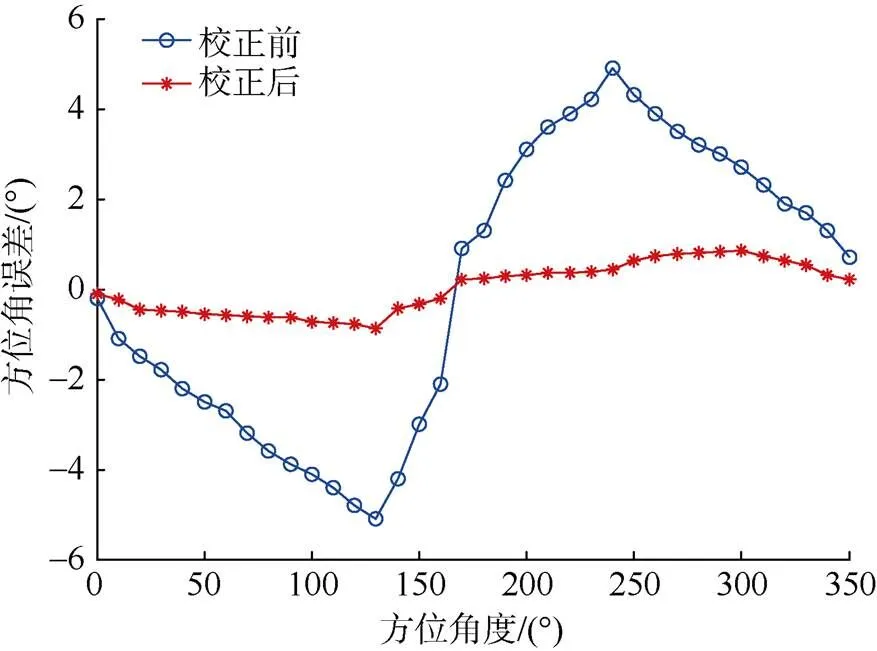
图8 方位角误差曲线

6 结论

a. 对煤矿井下随钻测斜仪测量模块中的加速度计和磁强计进行误差源分析并基于递推最小二乘，采用椭球拟合法、点积不变法和旋转平面拟合法的联合校正方法完成对随钻测斜仪的校正，俯仰角和方位角的测量精度提高了一个数量级。

b. 联合校正方法是一种低成本，计算方法简单，精度可靠，方便应用的校正，适用于煤矿井下随钻测斜仪校正。

请听作者语音介绍创新技术成果等信息，欢迎与作者进行交流

[1] GIZAWY E L. Wellbore surveying while drilling based on Kalman filtering[J]. American Journal of Engineering and Applied Sciences，2010，3(2)：240–259.

[2] 郝东，绳涛，陈小前. 三轴磁强计测量误差修正方法[J]. 航天器环境工程，2011，28(5)：463–466. HAO Dong，SHENG Tao，CHEN Xiaoqian. The error correction of three-axis magnetometer measurement[J]. Spacecraft Environment Engineering，2011，28(5)：463–466.

[3] 代刚. MEMS–IMU误差分析补偿与实验研究[D]. 北京：清华大学，2011. DAI Gang. MEMS-IMU error analysis compensation method and experiment research[D]. Beijing：Tsinghua University，2011.

[4] 郭卫，杨鹏飞，张武刚，等. 基于BP神经网络模型的MEMS加速度计误差补偿方法[J]. 中国测试，2018，44(3)：109–113. GUO Wei，YANG Pengfei，ZHANG Wugang，et al. Error compensation method for MEMS accelerometer based on BP neural network model[J]. China Measurement & Test，2018，44(3)：109–113.

[5] 晁正正，张晓明，马喜宏，等. 一种新的电子罗盘校准算法研究[J]. 传感技术学报，2019，32(1)：106–110.CHAO Zhengzheng，ZHANG Xiaoming，MA Xihong，et al. Research on a new electronic compass calibration algorithm[J]. Chinese Journal of Sensors and Actuators，2019，32(1)：106–110.

[6] 宋忠国，郑家欢，张金生，等. 基于粒子群优化的三轴磁强计非线性误差校正[J]. 传感器与微系统，2017，36(12)：40–42. SONG Zhongguo，ZHENG Jiahuan，ZHANG Jinsheng，et al. Nonlinear error calibration of three-axis magnetometer based on PSO algorithm[J]. Transducer and Microsystem Technologies，2017，36(12)：40–42.

[7] 陆欣，刘忠，张宏欣，等. 三轴MEMS加速度计的最大似然校正算法[J]. 国防科技大学学报，2017，39(5)：185–191. LU Xin，LIU Zhong，ZHANG Hongxin，et al. Maximum likelihood calibration for MEMS triaxial accelerometer[J]. Journal of National University of Defense Technology，2017，39(5)：185–191.

[8] 龙礼，张合. 三轴地磁传感器误差的自适应校正方法[J]. 仪器仪表学报，2013，34(1)：161–165. LONG Li，ZHANG He. Automatic and adaptive calibration method of tri-axial magnetometer[J]. Chinese Journal of Scientific Instrument，2013，34(1)：161–165.

[9] 江泽宇，谢洪波，文广超，等. 煤矿井下电磁波无线随钻轨迹测量系统设计与应用[J]. 煤田地质与勘探，2017，45(3)：156–161. JIANG Zeyu，XIE Hongbo，WEN Guangchao，et al. Design and application of electromagnetic radio MWD system of drilling track in coal mine[J]. Coal Geology & Exploration，2017，45(3)：156–161.

[10] 王成立，CHIKHOTKIN V F，卢春华. 随钻测斜仪误差补偿实验研究[J]. 煤田地质与勘探，2016，44(4)：147–152. WANG Chengli，CHIKHOTKIN V F，LU Chunhua. Error compensation of measurement while drilling inclinometer[J]. Coal Geology & Exploration，2016，44(4)：147–152.

[11] 邓志红. 惯性器件与惯性导航系统[M]. 北京：科学出版社，2012. DENG Zhihong. Inert components and inert navigation system[M]. Beijing：Science Press，2012.

[12] 刘艳霞，方建军，杨清梅. 基于椭球假设的三轴加速度计误差标定与补偿[J]. 传感器与微系统，2014，33(6)：52–54. LIU Yanxia，FANG Jianjun，YANG Qingmei. Three-axis accelerometer error calibration and compensation based on ellipsoid hypothesis[J]. Transducer and Microsystem Technologies，2014，33(6)：52–54.

[13] 郭鹏飞，华春红，任章，等. 基于递推最小二乘的航姿系统罗差校正[J]. 中国惯性技术学报，2008，16(1)：24–27. GUO Pengfei，HUA Chunhong，REN Zhang，et al. Magneticdeviation compensation using recursive least square for AHRS[J]. Journal of Chinese Inertial Technology，2008，16(1)：24–27.

[14] 龙礼，黄家才. 基于递推最小二乘法的地磁测量误差校正方法[J]. 仪器仪表学报，2017，38(6)：1440–1446. LONG Li，HUANG Jiacai. Recursive least square based online error calibration method in geomagnetic detection[J]. Chinese Journal of Scientific Instrument，2017，38(6)：1440–1446.

[15] 李翔，李智. 航姿参考系统三轴磁强计校正的点积不变法[J]. 仪器仪表学报，2012，33(8)：1813–1818. LI Xiang，LI Zhi. Dot product invariance method for the calibration of three-axis magnetometer in attitude and heading reference system[J]. Chinese Journal of Scientific Instrument，2012，33(8)：1813–1818.

[16] 李翔，王勇军，李智. 航姿系统矢量传感器非对准误差及其校正[J]. 传感技术学报，2017，30(2)：266–271. LI Xiang，WANG Yongjun，LI Zhi. Inter-triad misalignment of vector field sensors in attitude andheading reference systems and its calibration[J]. Chinese Journal of Sensors and Actuators，2017，30(2)：266–271.

[17] 李智，李翔. 基于椭球假设的三轴电子罗盘罗差补偿研究[J]. 仪器仪表学报，2011，32(10)：2210–2215. LI Zhi，LI Xiang. Research on magnetic deviation compensation of three-axis electronic compass based on ellipsoid hypothesis[J]. Chinese Journal of Scientific Instrument，2011，32(10)：2210–2215.

[18] 梁伟嘉，吝伶艳，刘宗伟. 基于椭球和平面拟合的随钻测量系统校正方法[J]. 煤炭技术，2016，35(9)：250–251. LIANG Weijia，LIN Lingyan，LIU Zongwei. Calibration method of measurement while drilling system based on ellipsoid and plane fitting[J]. Coal Technology，2016，35(9)：250–251.

Joint correction method of errors of MWD inclinometer in underground coal mine

QIAO Meiying1, WANG Bo1, XIAO Xuejun2, XU Chengkuan1, YAN Shuhao1

(1. School of Electrical Engineering and Automation, Henan Polytechnic University, Jiaozuo 454000, China; 2. Fourth Geological Team, Hebei Provincial Bureau of Coal Geology, Zhangjiakou 075100, China)

In order to reduce the error of measuring the drilling attitude angle parameter of MWD inclinometer in coal mine, a mathematical model of error compensation based on recursive least squares was established, the joint correction method of ellipsoid fitting method, dot product invariance method and rotation plane fitting method were used in the error compensation correction for MWD inclinometer. Numerical simulation experiment and double-axis turntable experiment were carried out on the developed MWD inclinometer, error compensation correction of experimental data was conducted with joint correction method, the maximum absolute errors of pitch angle and azimuth angle before correction are 4.7° and 5.1°, after correction are 0.8° and 0.9°, the corrected measurement accuracy meets the requirements of MWD inclinometer. Experimental results show that this method can be used to effectively compensate the error correction of MWD inclinometer in underground coal mine.

MWDinclinometer in underground coal mine; joint correction; the error compensation correction; pitch angle; azimuth angle

TE243

A

10.3969/j.issn.1001-1986.2020.02.030

1001-1986(2020)02-0202-07

2019-07-16；

2019-08-22

国家自然科学基金项目(61573129)；河南省教育厅重点科研项目(16A120004)

National Natural Science Foundation of China(61573129)；Key Research Project of Henan Provincial Educational Department(16A120004)

乔美英，1976年生，女，内蒙古乌拉特前旗人，博士，副教授，从事机器学习及时间序列数据分析的研究. E-mail：qiaomy@hpu.edu.cn

乔美英，王波，肖学军，等. 煤矿井下随钻测斜仪误差联合校正方法[J]. 煤田地质与勘探，2020，48(2)：202–208.

QIAO Meiying，WANG Bo，XIAO Xuejun，et al. Joint correction method of errors of MWD inclinometer in underground coal mine[J]. Coal Geology & Exploration，2020，48(2)：202–208.

(责任编辑 聂爱兰)