基于MQI评估系统的大班数学集体活动质量分析及其启示
李美芳 周 欣 杨志艳

[摘 要] 数学是学前儿童学习和入学准备的重要领域,也是学前教育质量监测的重要方面。MQI评估系统作为一种评估数学课堂教学质量的框架,体现了最新数学教育观念,突出了数学的学科特性和认知要求,强调儿童的主动参与和生成性的教学过程,可同时对教师的教和儿童的学进行评估。本研究使用MQI评估系统对我国幼儿园大班数学集体活动的质量进行考察,结果表明除数学意义建构和数学语言之外,数学丰富度领域各维度表现水平不高;教师对儿童行为进行处理和反馈的水平较低;大多数活动片段中不存在数学表达和语言上的错误及不严密性问题;儿童参与有意义的解释或者提问和推理较少,参与活动的认知要求不高。幼儿园大班数学集体活动质量受到集体教学中“教”与“学”的关系、教师对数学领域知识和儿童数学发展目标的认知、教师评价儿童数学思维的能力及师幼互动技巧、教师培训与考核的侧重点等因素的影响。我国学前教育界应重视数学教育活动的过程性质量,关注儿童数学学习过程性能力的发展,并应在借鉴MQI评估系统的基础上开发适合我国幼儿园数学教育实践的质量评估系统。
[关键词] MQI评估系统;教育质量监测;幼儿园数学教育;集体教学活动
一、问题提出
数学是学前儿童重要的学习内容和入学准备的重要领域,也是一些发达国家学前教育质量监测的重要方面。数学集体教学活动是教师有目的、有计划组织的通过儿童的参与和操作使儿童获得初步的数学概念并发展其解决与生活相关的数学问题的能力的一种数学教学活动。[1]首先,在幼儿园教育中,教师引导和儿童自主的学习活动都很重要,且这二者应有一种平衡,因此在幼儿园教育中集体教学活动仍占有重要的地位;其次,儿童在日常生活中获得的数学知识经验往往是感性和零散的,有计划地开展数学集体活动有利于儿童获得核心的数学经验,促进其数学概念的建构和发展;第三,数学集体活动目前仍然是幼儿园特别是大班数学教育的一种重要形式。此外,对为数不少的家庭中数学经验不足的儿童,集体活动能够起到重要的补偿作用。[2]对于如何评价数学集体活动的质量,近年来儿童数学学习和能力方面的相关研究为我们提供了方向。比如,全美数学教师理事会(NCTM)2000年颁布的《美国数学学校教育的原则和标准》明确提出了从学前到中学数学学习的核心知识经验和5种过程性能力:问题解决、推理与证明、数学交流、数学关联、数学表征。[3]大规模的国际比较研究,如国际学生评估项目(PISA,2012)和国际数学与科学趋势研究项目(TIMSS,2015)也明确提出了数学学习过程中的基本能力包括交流、数学化、表征、推理和论证、运用策略解决问题、使用符号、正式语言和技术语言与运算、使用数学工具等。中国基础教育质量监测中心启动的数学教育质量监测明确了数学思维与问题解决导向等原则,不仅关注学生数学基础知识和基本技能的掌握,而且关注学生抽象能力、推理能力和创新能力等的发展,引导学生建立数学与外部现实世界的联系,充分发展学生提出问题、分析问题以及运用数学思想和方法解决现实生活问题的能力。[4]周欣等人探究的学前儿童数学素养监测指标体系包含数学知识技能(数和运算、形状和空间、模式、测量)、过程性能力(联系、推理与验证、表征与交流)、态度和学习品质(兴趣、专注、坚持、反思)三个方面,明确了学前末期儿童应具有的数学素养。[5]但目前幼儿园的数学集体活动并没有很好地关注和促进儿童早期数学能力的发展,关键原因之一是当前对幼儿园数学集体活动质量的评价仍然停留于传统的关注教师的教、關注儿童掌握数学知识技能等学习结果层面,为此应引入以儿童早期数学能力方面的最新研究成果为理论基础的新的评估工具,改革传统的评价方式,以改变我国幼儿园数学教育当前这种重教轻学、重知识结果轻能力过程的现象。
MQI(Mathematical Quality of Instruction)评估系统由密歇根大学希尔(Hill)教授领衔开发,在多年课堂实践研究的基础上,于2010年正式出版。该评估体系适用于观察K(5~6岁)到九年级的数学课堂教学,是目前应用最广泛的评估工具。MQI评估系统体现了探索性学习的导向和学生中心的取向,包含数学内容丰富度、学生行为处理、错误和不严密性、学生有意义学习参与度四个领域13个维度(2010版),每个领域和维度都有详细的水平划分标准。[6]之后的研究者使用该工具时对该框架略有改动,如增加了第五个领域——发展连贯性的教学轨迹;[7]2014年正式版本中,在第一个领域增加了数学意义建构维度,第四个领域改为与州共同核心标准一致的学生表现,并在该领域中增加了2个维度(学生就这一部分中的数学进行讨论,学生解决情境化问题)。[8]目前MQI(2014版)已有免费在线培训资源。MQI评估体系反映了当前数学课堂质量评估工具中共同的质量要素:强调儿童对基本数学概念的理解;通过创设问题情境发展儿童解决问题的能力;鼓励儿童的表征、表达和沟通协商;围绕数学内容有积极的师幼互动。与其他数学课堂质量评估工具相比,使用MQI评估幼儿园集体数学活动具有一定的优势。早期的《建构主义学习环境调查问卷》(Constructivist Learning Environment Survey,CLES)由学生填写他们对课堂学习环境的感受,以此评估课堂教学质量,[9]相对较为主观。MQI直接对课堂或录像进行观察分析,较为客观,并能提供丰富的描述性资料。此外,CLES与评估STEM课堂教学的教师观察工具UTOP(U Teach Observation Protocol)[10][11]以及测量数学和科学课堂是否符合改革要求的教师观察工具RTOP(Reformed Teaching Observation Protocol),[12]作为跨学科的评估工具,更多反映了一般性的课堂结构和课程实施过程,而MQI能够突出数学活动的学科特性。《教师-学生学习互动编码》(Coding of Academic Teacher-Student Interactions,CATS)是为了检验特定的课程效果而编制的工具,[13]CATS与RTOP对教学有明确的指向和要求,MQI作为一般性数学教学活动的评价工具,则不限定数学活动类型。TRU(Teaching for Robust Understanding in Mathematics)课堂评价模型强调学生对概念的理解和教师对学生理解的支持,[14]未能全面反映数学教和学的重要方面。波士顿(Boston)等人开发的教学质量评估工具包(Instructional Quality Assessment,IQA),通过课堂观察和学生作业两类资料,对教学任务的认知要求、任务实施、数学思维和推理解释以及教师期望进行评价,[15]其中收集儿童作业样本的方法不适用于学前阶段的评估。萨拉马和克莱门茨(Sarama & Clements)开发的《早期数学课堂观察工具-环境和教学》(Classroom Observation of Early Mathematics- Environment and Teaching,COEMET),主要从教师教学的角度对数学核心、组织-教学方法-互动、期望、引发儿童解决问题、支持儿童的概念理解、延伸儿童的数学思想、评估和调整教学等方面进行评估,[16]MQI则可同时对教师的教和学生的有意义参与情况进行评估。
本研究采用MQI(2014版)的框架来观察和评估我国幼儿园大班数学集体活动质量,主要拟回答以下问题:从MQI评估系统的评价领域和维度来看,目前我国幼儿园大班开展的数学集体活动在各个领域和维度上的总体表现如何?如何根据数学集体活动评估的结果提出有针对性的建议?借鉴MQI评估我国幼儿园数学集体活动质量,是否需要修订?
二、研究方法
(一)研究对象
本研究的研究对象为来自上海市2所一级园(1所公立,1所私立)和2所二级园(1所公立,1所私立)的18位大班教师实施的数学集体活动。教师的基本情况见表1。教师根据本园教学计划,参照上海市二期课改大班课程的要求,自主设计和组织数学集体活动,研究者不对活动进行限定和指导。本研究最终录制的数学集体活动涉及了分类(2个)、加减运算(4个)、模式(3个)、测量(4个)、空间和图形(4个)、数字符号(3个)等数学内容,包含了大班幼儿数学发展的核心经验。上海市一级园和二级园占本市幼儿园总数的近90%,四所园集体教学活动的抽样一定程度上反映了当地数学集体教学活动的真实情况。
(二)研究工具
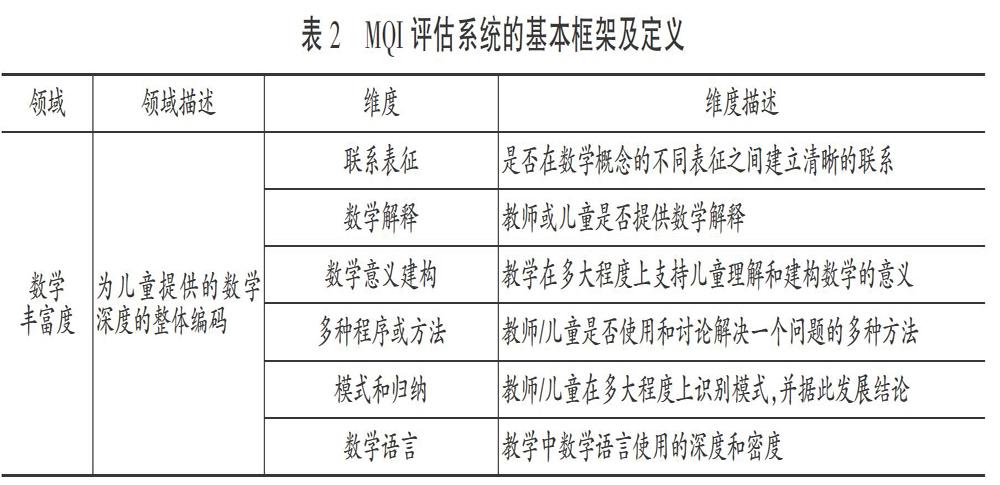
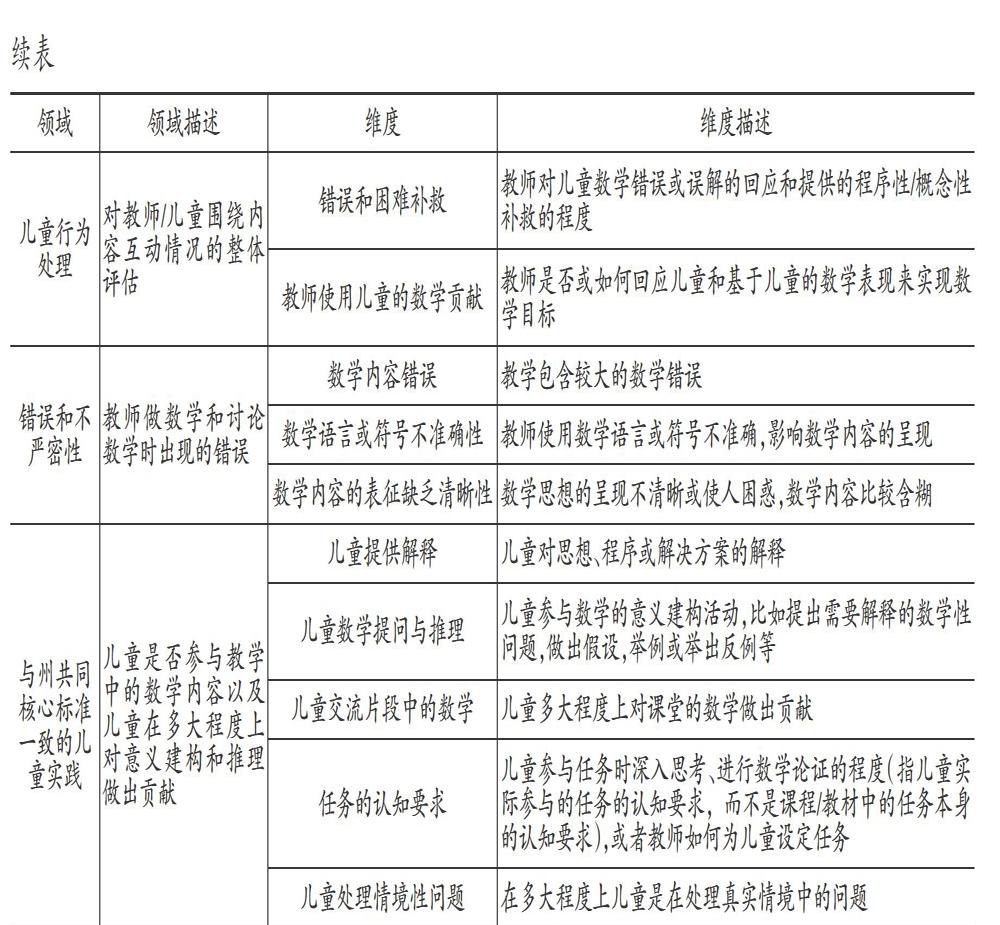
与2010年的版本相比,2014年版的MQI评估体系更为突出儿童参与,并将2010年版本各个维度低水平中没有出现的情况分离出来,分为没有出现、低、中、高四个水平。[17][18]本研究使用的是2014年版的MQI评估体系,其领域与维度的内涵见表2。
MQI评估系统自颁布以来被广泛用于中小学的数学课堂评估,具有较好的内容效度和结构效度。验证教师数学教学知识(MKT)和数学教学活动质量(MQI)关系的质性研究发现,MKT得分较高的教师能够提供较丰富的数学解释,更恰当地使用表征并在表征之间建立联系,强调关键的数学思想,同时这些教师较少出现或不会出现细微的数学错误或不严密性。量化研究发现,MQI得分与教师的数学知识及儿童的学习都存在正相关,[19][20]MQI得分与评估STEM学科的观察工具UTOP的得分相关性较高(r=0.85),[21]与一般的课堂观察工具CLASS相关性也较高(r=0.69)。[22]目前已有将MQI评估系统用于学前阶段的实证研究。本研究的两位评分者考察了MQI工具开发的过程以及使用MQI工具所做的研究,并参加了哈佛大学教育政策研究中心的MQI(2014年版)在线培训,研究者与工具开发者在示例片段上的编码一致性均在80%以上。本研究的两位评分者对所有的活动片段分别进行编码,各个领域、维度和整体编码上的一致性在80%~92%之间,具有较高的一致性。
(三)研究过程
本研究首先请18位大班教师根据大班儿童的年龄特点和教学计划,自主设计和组织集体数学活动,然后由一位研究者对数学活动进行观察,并在教师同意的情况下使用摄像机进行录像,同时记录教学活动现场的信息。录像根据教师姓名、日期及时编码并保存至电脑。大多数数学集体活动在上午9点至11点之间进行,该时间段是幼儿园常规中用于组织集体活动的时间,不受其他事务的干扰。
(四)数据收集与处理
本研究共录制了20次数学集体活动,每次活动时间为20~35分钟。研究者把所有视频转录为文本,参照视频的时间刻度和文本的语义,考虑编码者对活动内容记忆的保持时间,以7.5分钟为一个教学片段。[23]如果数学集体活动的最后一个片段少于3.75分钟,则将其与上一片段合并,如果最后一个片段多于3.75分钟,则单独作为一个片段编码。本研究共产生85个教学片段。研究者对每一个片段按照姓名、日期、片段序号进行编码,如GJJ2018090201,对每一教学片段按照表2所示的评估框架进行评分。MQI作为质性观察工具,需要研究者根据片段中各维度的观察要点的表现情况进行评分。四个领域和16个维度分为没有出现(Not Present)、低(Low)、中(Mid)、高(High)四个水平。[24]MQI整体编码和四个领域、16个维度单独评分,以数学丰富度领域为例,联系表征、数學解释、数学意义建构、多种程序或方法、模式和归纳、数学语言6个维度依据各自的评估标准分别编码。数学丰富度的整体水平有一个独立的评估标准,不是6个维度的平均分。最终,每个活动片段产生的数据包括:教学活动基本信息,四个领域16个维度共20项编码,以及片段在各维度的观察要点上的具体表现的质性资料。
三、研究结果与分析
(一)数学丰富度领域的表现情况
从图1可知,在数学意义建构维度上,中、高水平的片段分别占9.4%和47.1%,说明教师和儿童较为持续地关注数学意义的建构,如说明数字的意义、数字之间的关系、情境和代表它们的数字/程序之间的关系、数学想法之间的联系或想法与表征之间的关系等,低水平或没有出现数学意义建构的片段分别占29.4%、14.1%。在数学语言维度上,教师正确、流畅使用数学语言,数学语言密度较高,教师提示儿童正确使用术语的片段占40.0%,教师使用中等密度的数学语言的片段占22.4%,教师使用数学语言的密度较低、没有使用数学语言或使用错误的片段分别占29.4%、8.2%。数学集体活动中没有出现联系表征、数学解释、多种程序或方法、模式和归纳的片段较多。94.0%的片段中没有出现联系表征的情况,出现表面的联系的片段占2.4%,出现1例详细的联系表征或以详细解释多种表征为特征的片段分别占1.2%、2.4%。52.9%的片段中没有出现教师或儿童的解释,出现1次解释的片段占29.4%,出现2次简单的解释或一次深入解释的片段占8.3%,出现多个解释,以解释为主要特征的片段占9.4%。没有出现多种程序或方法的片段占56.5%,教师或儿童简单提到第二种方法但没有展开的片段占16.5%,出现或讨论了多种方法或程序的片段占23.5%,讨论多种方法或程序的联系、适用条件、优缺点的片段占3.5%。没有出现模式和归纳的片段占70.6%,教师和儿童注意模式、进行表面上的归纳的片段占14.1%,有进行归纳、延伸模式但不彻底的片段占10.6%,从具体的例子中发展归纳,详尽描述模式如何产生的片段占4.7%。在对数学丰富度的整体估计中,没有出现数学丰富性元素的片段较少(8.2%),低(31.8%)、中(28.2%)、高(31.8%)水平的片段数量差别不大。
数学丰富度的6个维度包含了对教师和儿童表现的评估,分别对教师和儿童在各个维度上的表现进行统计,结果显示在85个教学活动片段中,教师和儿童对数学思想或表征进行简单的关联的片段各有1个,能够说明不同的数学思想或表征的关联或区别的片段分别为3个和0个。教师和儿童简单地关注数学意义的片段分别为18个和15个,出现了较详尽地关注意义的例子的片段各为8个,出现持续关注数学概念、数量、情境等意义的片段分别为38个和30个。出现1次教师或1次儿童解释的片段分别为11个、17个,出现2次教师或2次儿童解释的片段为5个和4个,出现多次儿童解释的片段为8个,没有出现教师多次解释的片段。儿童简单提到两种方法的片段为14个,儿童提出多种方法的片段为20个,没有出现教师提出的多种方法。教师比较不同方法的效果、适宜性或优缺点的片段有3个,没有儿童对不同方法进行比较归纳的情况,教师或儿童简单进行归纳的片段分别为11个和1个,注意、延伸或解释模式或规律的片段分别为8个和1个,仔细地从具体的例子中进行归纳、描述模式或规律是如何产生的片段分别为4个和0个。教师和儿童使用数学语言密度较低的片段分别为15个和10个,数学语言为中等密度的片段分别为12个和7个,教师流畅地使用数学语言,鼓励和示范儿童使用数学语言的片段为34个,儿童频繁、流畅地使用数学语言的片段有30个。
(二)儿童行为处理领域的表现情况
从图2可知,在儿童错误、困难补救维度上,教师忽略儿童的错误或者只是进行简单修正,如告诉儿童答案对错的片段占57.6%,简单地从程序步骤上纠正错误或概念补救的片段占18.8%,较详细地进行程序补救或共同关注错误的片段占15.3%,确认儿童发生错误的根源并利用这些错误强调对重要的数学概念和程序的理解的片段仅占8.3%。教师使用儿童贡献方面,14.1%的片段中主要是教师表达,很少有儿童的表达。教师对儿童进行形式上的回应的片段占38.8%,比如儿童表达主要是基本的计算或答案确定的问题,或者儿童有不同的答案或解释,教师除了确认正确的一个之外,不利用儿童错误的想法。教师理解儿童所说,激发儿童思考和澄清,让儿童发表评论,拓展和强化儿童的表达,并将儿童思想融入数学内容的发展的片段占24.7%。对儿童行为处理的整体估计中,中、高水平的片段占47%,没有出现儿童行为处理或进行低水平的处理的片段共占53%。
(三)错误和不严密性领域的表现情况
从图3可知,97.6%的片段没有出现数学内容上的錯误,出现简单的内容错误但不影响该部分数学内容的片段占1.2%,出现内容错误且影响该部分数学教学的片段占1.2%。83.5%的片段没有出现数学语言、一般语言或符号的错误,有少数暂时的错误不影响数学内容的进行或者教师及时进行了纠正的片段占15.3%,出现了语言、符号的不准确且影响了数学内容的进行的片段占1.2%。74.1%的片段中教师发起的任务和对任务的表述是清晰的,出现简单的表述不清晰但不影响数学内容说明的片段占24.7%,出现了表述不清晰并使数学内容模糊的片段占1.2%。对错误和不严密性领域的整体估计中,没有出现错误的片段占64.7%,出现小的偶然性错误但不影响数学的清晰性的片段占35.3%,没有出现多个、持续或较严重的错误的片段。
(四)与州共同核心标准一致的儿童实践领域的表现情况
从图4可知,没有出现儿童解释的片段占60%,出现1个或2个儿童简单的解释的片段占28.2%,较持续、经常出现儿童解释的片段占4.7%,而以儿童的解释为主要特征的片段仅占7.1%。没有出现儿童提出数学上需要解释的问题,或者对某一问题持反对意见,或者对活动中讨论的数学问题进行推理的行为片段占47.1%。出现1个或2个儿童提问与推理行为的片段占37.6%,持续、频繁出现这种行为的片段更少(9.4%)。儿童提问、推理比较突出的片段仅占5.9%。儿童交流数学方面,儿童仅提供1个或2个词的答案或者对步骤进行部分描述的片段占50.6%,出现了儿童中(14.1%)、高(24.7%)水平的贡献的片段,如儿童很少公开呈现方法,提出数学上需要解释的问题,描述词语的意义,提供一个解释,讨论解决方案或评论他人的推理等较少。67%的片段中儿童参与的任务认知要求不高,更多是回忆或复制事实、规则,多是听取教师的陈述,儿童表达较少,儿童的表达多是对教师提出的限定问题的简短回答,如对错、是否、同意不同意等,或者虽然任务不是常规化的,但是教师给儿童的支架过多。儿童实际参与认知要求较高的任务,如通过参与活动决定数学概念、过程和关系的意义,在不同表征和概念之间建立联系,做出或检验假设,寻找模式,解释和论证等的片段仅占22.4%。
四、讨论
(一)幼儿园数学集体活动的整体质量状况
1. 教师和儿童在关注数学意义和使用数学语言方面的表现。
从数学丰富度领域的结果可知,虽然教师和儿童能较为持续地关注意义,如关注数量、数字符号、表达式的意义或解决方法、答案的合理性等,但是注意力较多地集中在对符号含义本身进行描述,且更多从工具性理解(语义性或程序性理解)的角度进行意义建构,如符号A代表什么意思或规则R怎么操作,较少从关系性理解的角度对符号指代物的意义和规则的逻辑依据进行深刻的探索。[25]这是因为工具性理解的教学方式易记忆、易模仿,可以较快地实现数学知识技能的传递。然而,幼儿期的数学教育与学习并不在于符号性知识的简单传递,而在于让幼儿建立与数学符号性知识的意义关系。这需要依赖个体性经验,而非知识的逻辑体系。[26]教师与儿童讨论数字符号、概念、解决方法或答案的合理性时,必须联系幼儿的实际生活经验或已有数学经验,才能使幼儿真正理解并内化。
数学语言系统包括符号语言、文字符号和图表语言三类语言,文字语言通俗易懂,数学符号虽抽象但十分简洁,图表语言更具直观性,一种数学思想内容的完整表达常是这三种语言的优势互补和有机融合。[27]然而,数学语言维度的统计显示教师大多是使用口头语言描述数学概念或思想,较少利用符号语言、文字语言或图表多种语言的优势。此外,数学集体活动中教师和儿童使用数学语言传递数学内容时,教师较为关注儿童数学语言的规范性,通常为儿童提供较多的支架,帮助他们正确、完整地表述数学内容,这有助于儿童数学语言能力的发展。但是,教师很少运用策略促进儿童思考和交流,比如巧用提问式数学语言,推动幼儿提出问题-猜测-证明的思维过程;向幼儿呈现数学认知冲突,激发幼儿主动解决问题;要求幼儿运用数学语言分享经验和策略等。[28]这可能是因为教师设定的教学目标更关注知识技能,或者教师所做的活动准备内容比较局限,教师没有深入理解活动中的数学概念、方法,不能灵活使用多种语言来表达,还有可能是教师缺少使用数学语言的技巧和策略。
2. 教师和儿童在联系表征、数学解释、多种解法、模式和归纳维度上的表现。
表征是交流的方法,也是强有力的思维工具,在不同的数学表征之间建立联系或在思想和表征之间建立联系的过程,有助于加深儿童对数学的理解。[29]然而,本研究显示数学集体活动中较少出现联系表征的情况,可能是幼儿园数学活动内容比较简单,很少有需要转换表征的任务情境,或者该指标的要求与幼儿阶段的实际情况不符,因为早期数学中关联的重点是将儿童经验中的非正规数学观念与学校学到的数学观念之间建立联系,包括数学与日常生活的联系,[30]同时学前儿童常用的表征方式虽然有口头或书面语言、图画、图符、自创或通用的数字符号等,但是他们尚不能在多种数学符号体系之间进行自由的转换。儿童借助图形或文字表述解释自己的解题过程,能帮助他们清楚地描述自己的思维并使之更为精确。[31]然而,本研究显示数学集体活动中教师或儿童解释都较少,可能是教师更关注数学知识技能的教授而不关注数学知识产生的过程,也有可能是出現的许多解释不正确或不完整,没有计算在内。从不同的角度思考问题,运用不同的知识和策略解决问题,有助于加深儿童对知识内在联系的认识,有利于知识的迁移。本研究显示数学集体活动中较少出现一个问题的多种解法,可能是开放性的问题或任务较少,也可能是教师没有鼓励儿童探索多种解决办法,或者儿童提供的许多方法或答案不正确,没有计算在内。数学归纳推理是通过观察和组合特殊事例的量性特征发现一类事物的量化模式的创造性思维过程,[32]对感性的、零散的、具体的数学经验和数学思想进行提升和总结,也是组织数学集体活动的重要作用。但是,在本研究大多数片段中没有出现模式和归纳的例子,且几乎所有的归纳是由教师进行的。这说明在幼儿园数学集体活动中,教师对儿童数学思维的发展缺乏关注。
3. 教师对儿童行为的处理和反馈。
绝大多数活动片段中教师对儿童的错误只是进行简单的修正,同时也较少利用儿童的思想或贡献开展接下来的活动。这与相关研究发现师幼课堂互动中“教育支持得分最低”的结论较为一致。[33]无论教师采取开放式还是封闭式提问,教师处理儿童的回答与反应时终止性理答行为都多于拓展性理答行为,教师对不同年龄段幼儿的理答行为都仅仅关注将准确的信息传达给幼儿。[34]究其原因,一方面可能是教师更看重正确知识的传授而不关注儿童的思维过程,另一方面可能与教师掌握数学领域知识的情况有关。如果教师对儿童数学发展目标和数学教育内容并不清楚,且缺乏对数学概念之间关系的认识,[35]那么就不太可能为幼儿提供高质量的教育支持。此外,教师能否准确判断儿童的知识能力和思维也会影响数学活动中反馈的质量。如果教师对幼儿数学能力的了解仅仅停留在表面上,比如简单的数数、认识形状,对幼儿更深层次的思维能力没有很好的观察和把握,[36]那么就很难在数学活动中针对不同儿童给出即时有效的反馈。
4. 数学语言和符号使用上的错误和不严密性。
整体的错误和不严密性估计的水平与该领域3个维度的得分情况一致,绝大多数活动片段没有出现数学内容、语言或表达上的错误。数学语言、符号的运用对个体思维和认知发展有重要影响,它是儿童从具体数学思维向抽象数学思维转化的标志,也是儿童与成人在数学方面进行交流的基础。本研究结果表明,教师能够较好地使用简单的数学术语和运用一般语言表达数学思想。由于大班数学活动中经常使用的数学符号和术语如“+”“-”“=”“大于”“等于”“小于”或者角、图形、长度、高度等都比较简单,教师和儿童也经常使用一般性语言来传递数学概念和思想,所以绝大多数的片段中都没有出现错误,也可见错误和不严密性领域对数学活动质量高低没有区分度和敏感性。将MQI用于教师培训的研究也发现,除了错误和不严密性之外,接受培训的教师在其他各个维度上都有所提高。[37]这说明错误和不严密性领域可能并不是区分幼儿园数学活动质量高低的重要指标。[38]
5. 与州共同核心标准一致的儿童实践方面的表现。
本研究结果表明,在儿童有意义参与方面,儿童提供解释、儿童提问与推理、儿童交流数学、认知要求、儿童参与情境问题的水平不高。斯蒂格勒和希伯特(Stigler & Hiebert)对一些国家和地区的国际数学与科学趋势研究(TIMSS)视频(每个国家或地区100节课)的分析也发现,呈现给学生的任务中,缺乏数学上的连贯性或认知要求水平较低的任务占大多数,在教学中基本没有为学生提供建立数学方面的联系的机会。[39]大部分观察到的教学任务和教学都是没有联系意义的机械过程,只有38%的课堂任务为儿童提供了参与高级思维和推理的机会,30%的实际教学中出现了儿童的高级思维和推理。[40]出现这种情况的原因可能是多方面的,比如幼儿先前数学经验不足,不能在活动中进行主动的探索、提问、推理验证和交流与表达等;教师对数学活动中教和学关系的定位不准,不能将教师传授知识的过程转变为幼儿发现问题、理解问题、解决问题的过程;整合课程背景下的幼儿园数学教育虽然很“活”,但是捕捉数学方面的点也很“难”,即整合课程下数学教育面临被“淡化”的局面;[41]许多教师的活动目标不清晰,组织方式较为单一,对幼儿的已有经验把握不太准确,导致数学活动开展的频率少且质量较低。[42]此外,由于数学集体活动中儿童的表现会受到教师行为的直接影响,所以教师对儿童数学发展目标的认识和对数学领域知识的掌握情况,以及对儿童数学能力和思维进行评价的能力,教师与儿童的互动技巧等都有可能会影响数学集体活动中儿童的参与情况。
综上,就本研究结果来看,在数学集体活动中教师和儿童在关注数学意义和使用数学语言方面表现较好,且两者的表现具有一致性;基本没有出现错误和不严密性,但对儿童数学学习的过程性能力关注较少,围绕数学内容的师幼互动质量较低,活动过程中儿童的有意义参与较少。
(二)使用MQI评估幼儿园数学集体活动质量的局限性
从研究结果及讨论中我们发现,在幼儿园数学教育领域使用MQI系统,存在如下需要改进的方面:第一,需要对联系表征指标的定义和要求进行修订;第二,多种程序和方法维度可针对教师和儿童提出不同要求,因为对某个问题的多种解法大多是由儿童想出的,而对多种解法进行比较和总结都是由教师进行的,且对学前儿童来说,“比较和总结多种不同方法”这一要求太高;第三,错误和不严密性领域并不是区分幼儿园数学集体活动质量高低的重要指标;第四,检验MQI评估学前数学活动的适宜性的研究发现,在编码一致性较高的情况下,MQI的评分差异受幼儿园教师个人教学实践特点的影响较大,[43]如教师的教育信念、教学方法等。此外,数学教学活动片段的质量还可能受到数学内容、教学环节和任务情境的影响,因为不同类型的任务为儿童提供的学习机会不同。[44]目前MQI评估系统尚未考虑这些方面的影响,将来还有必要进一步修订和完善。
五、教育建议
在影响我国幼儿园大班数学集体活动质量的因素中,首先是我国传统的集体教学活动历来重“教”轻“学”;其次是有的教師对儿童数学发展的年龄目标可能不太清楚,数学领域知识架构不完善,对儿童数学能力和思维水平的评价不太准确,缺乏师幼互动的技巧;再次是目前对幼儿园教师的培训及考核都可能更侧重教师的活动设计与组织能力,一定程度上忽略了教师观察、评估和支持儿童学习的能力。此外,MQI评估体系在学前阶段的适用性也会影响对数学集体活动质量的准确评价。据此,本研究提出以下教育建议:
第一,实践中应重视对数学集体活动的过程性质量的考察。幼儿园结构性质量往往是通过过程性质量与儿童相互作用来影响儿童发展的。教育质量的过程性变量对儿童发展的影响比结构性因素大,应该成为托幼机构质量评价中最重要的部分。[45]对数学集体活动质量的考察应更关注活动的过程性质量,如数学活动目标是否依据对儿童的观察记录和分析制订;是否根据儿童的发展状况和个体情况调整目标;活动情境是否来源于幼儿真实的生活经验;活动中是否有围绕数学内容的高质量师幼互动(如教师幼儿平等对话,活动面向全体幼儿,尊重幼儿个别化差异,教师创造环境和提供支持材料,鼓励儿童的数学探索、思考和表达等)。此外,教师评价体系也应包括这些过程性质量要素内容,引导教师关注与幼儿在数学活动中的互动过程,充分挖掘数学活动中师幼互动过程的教育价值。
第二,转变重“教”轻“学”的传统观念,强调儿童数学学习过程性能力的发展。观念是行动的先导,教师首先要转变集体活动中重“教”轻“学”的传统观念,数学活动的设计与实施应围绕儿童的学习来进行。其次是加强教师对儿童数学素养的认识和了解,比如我国学前儿童数学学习与发展监测框架中提出的知识技能、过程性能力、学习品质三维发展目标。再次可以在教师培训中使用MQI等体现新的数学教育理念的评估工具,提高教师在集体活动、个别化活动和一日生活中对高质量的数学活动特征的重视程度和敏感性,突出儿童解决问题的过程性能力(联系、推理与验证、表征和交流),实现数学教育从强调知识获得到发展儿童能力的转变。比如,教师在设计数学活动时更多地考虑与儿童的真实生活有关的真实情境和开放性的数学问题;活动过程中为儿童提供高水平的思考和推理机会,鼓励儿童在概念之间建立联系,让儿童参与解释,完成有一定认知要求的任务;教师认真倾听和了解儿童的思维过程;正确使用数学语言,或使用日常语言说明数学概念,并在数学语言和日常语言之间建立联系或做出区分;鼓励儿童使用不同的表征,并明确它们之间的对应关系。此外,在教师培养中还可以增加教师观察评价儿童的方法和师幼互动技巧等内容,这是教师在教学活动中支持幼儿学习的重要条件。
第三,借鉴MQI评估系统,开发适合我国幼儿园数学教育实践的质量评估系统。借鉴MQI系统评估我国幼儿园数学集体活动时可以对一些指标进行修订,如将联系表征的要求改为我国学前儿童数学监测体系中的指标——“发现生活情境中的数学问题,或把已有的数学知识和经验迁移到新的问题情境中”;[46]把 “对一个问题给出不同种类的解题策略”作为评估儿童的指标,把“比较不同方法间的效率、适用性和简便性”作为考察教师的指标;把错误和不严密性领域缩减为一个维度等。此外,较完整的评估体系还应包括数学活动的背景信息,如数学方面的特定规范、活动领域内容、教学方法、任务情境及教师个人实践特征等方面的详细资料,[47]以便对数学集体活动做出更为客观准确的评价,从而更好地为提升教学活动质量服务。
参考文献:
[1][2]周欣,黄瑾,杨宗华.幼儿园综合课程中的数学教育[M].南京:南京师范大学出版社,2016: 45,46.
[3][29][30][31]全美数学教师理事会.美国数学教育的原则和标准[M].蔡金法,译.北京:人民教育出版社,2004:10,109,121,125.
[4]杨涛,辛淘,罗良,等.义务教育数学教育质量监测的探索与思考[J].数学教育学报,2018,27(5):1-7.
[5][46]周欣,黄瑾,郭力平,等.我国学前儿童数学监测指标体系的构建[J].学前教育研究,2018(10):14-23.
[6]周九诗.美国数学教学质量评估系统评介[J].外国中小学教育,2017(3):56-60.
[7]CHARALAMBOUS C Y, HILL H C. Teacher knowledge, curriculum materials, and quality of in-
struction: unpacking a complex relationship[J]. Journal of Curriculum Studies,2012,44(4):452.
[8][17][21][22][23][24]CHARALAMBOUS C Y, LITKE E. Studying instructional quality by using a content-specific lens: the case of the mathematical quality of instruction framework[J]. The International Journal on
Mathematics Education,2018,50(5):447-450.
[9]ASNAKW TAGELE. An assessment of mathematics classroom teaching-learning process: consis-
tency with constructivist approach[J]. Ethiopian Journal of Education and Sciences,2017,2(12):6.
[10]曹慧,毛亚庆.美国UTOP课堂教学质量评估系统的探索与反思[J].全球教育展望,2017(1):79-89.
[11]WALKINGTON C, MARDER M. Using the UTeach Observation Protocol (UTOP) to understand the quality of mathematics instruction[J]. The International Journal on Mathematics Education,2018(2):1-13.
[12]BOSTON M, BOSTIC J, LESSEIG K, et al. A comparison of mathematics classroom observation protocols[J]. Mathematics Teacher Educator,2015,3(2):154-175.
[13]DOABLER C T. Measuring instructional interactions in kindergarten mathematics classrooms through a direct observation system[J]. Dissertations & Theses-Grade works,2010(5):132.
[14]周九诗,鲍建生.美国“TRU”课堂评价模型介绍及其启示[J].外国中小学教育,2016(12):52-56.
[15][40]BOSTON M. Assessing instructional quality in mathematics[J]. Elementary School Journal, 2012,
13(1):76-104.
[16]SARAMA J, CLEMENTS D H. Manual for classroom observation(COEMET)-Version 3[R]. un-published version,2007:15-19.
[18]HILL H C, BLUNK M L, CHARALAMBOUS C Y, et al. Mathematical knowledge for teaching and the mathematical quality of instruction: an exploratory study[J]. Cognition and Instruction,2008,26(4):
430-511.
[19]KANE THOMAS, STAIGER DOUGLAS O. Gathering feedback for teaching: combining high-quality observations with student surveys and achievement gains[J]. Bill & Melinda Gates Foundation,2012(3):36.
[20]BLAZAR D, LITKE E, BARMORE J. What does it mean to be ranked a “high” or “low” value-added teacher? Observing differences in instructional quality across districts[J]. American Educational Re-search Journal,2016,53(2):324-359.
[25]馬复.试论数学理解的两种类型:从R·斯根普的工作谈起[J].数学教育学报,2001,10(3):50-53.
[26][41]赵振国.幼儿园整合课程中的数学教育:基于教师的视野[J].学前教育研究,2012(7):43-44.
[27]邵光华,刘明海.数学语言及其教学研究[J].课程·教材·教法,2005,25(2):37-38.
[28]赵琳,黄瑾.幼儿园数学集体教学活动中教师数学语言的特征与发展[J].学前教育研究,2014(7):46.
[32]李兴贵,王新民.数学归纳推理的基本内涵及认知过程分析[J].数学教育学报,2016,25(1):89.
[33]蒋路易,郭力平,吕雪.CLASS视角下师幼互动研究的元分析:基于中国14省市892名教师的师幼互动质量评估结果[J].学前教育研究,2019(4):39-40.
[34]孙倩.集体活动中幼儿教师理答行为的现状与改进[J].学前教育研究,2011(9):60-61.
[35]李娟,张丽芳,刘娇娇.幼儿园教师数学领域内容知识考察[J].学前教育研究,2016(11):57.
[36]熊庆华,庞丽娟,陶沙,等.教师对幼儿数学能力评价准确性的研究[J].学前教育研究,2003(2):30.
[37]KRAFT M A, HILL H C. Developing ambitious mathematics instruction through web-based coaching: an experimental trial[R]. Harvard University Working Paper,2017:38-39.
[38][43][47]PANAYOTA M, BRAIN F F, HELEN P. The Mathematical Quality of Instruction(MQI) in kindergarten: an evaluation of the stability of the MQI using generalizability theory[J]. Early Education and
Development, 2018,29(6):893-908.
[39]HIEBIERT J, STIGLER J W. Improving mathematics teaching[J]. Educational Leadership Journal of
the Department of Supervision & Curriculum Development,2004,61(5):12-16.
[42]田方.对集体教学活动中师幼互动现存问题的分析与建议:以S省为例[J].教育导刊(下半月版),2016(2):28-30.
[44]DOYLE W. Academic work[J]. Review of Educational Research,1983,53(2):159-199.
[45]周欣.四国和我国港台地区幼托机构过程性教育质量标准的分析和比较[J].早期教育(教师版),2003(2):5.

