基于不动点原理的电压稳定性分析方法

李凡，汪芳宗，温柏坚

(1. 三峡大学 电气与新能源学院，湖北 宜昌 443002；2. 广东电网有限责任公司信息中心，广东 广州 510080)

自20世纪90年代以来，有关电力系统电压稳定性的研究已取得了很大的进展。迄今为止，研究人员已提出了多种多样的电压稳定性分析方法以及电压稳定性指标[1-16]。其中，基于戴维南等值的电压稳定性分析与监测方法受到了广泛关注[17-25]。1999年，Khoi Vu等学者率先提出了基于局部量测的戴维南等值参数在线辨识及电压稳定监测方法[6]。此后，各国学者在此基础上不断进行改进和完善，提出了各种改进的戴维南等值参数计算模型和方法[20]；然而，现有的、基于就地量测的戴维南等值参数辨识方法均是建立在以下假设的基础上：相邻2个状态点或时间断面之间的戴维南等值参数不变。显然，这种假设在实际中是不成立的，因此，如何对动态变化的戴维南等值参数进行准确跟踪，仍然是一个未能得到彻底解决的问题[7-9]。

为避免上述问题，文献[19]提出了基于时域仿真的戴维南等值参数跟踪计算方法。理论上，这种基于时域仿真的戴维南等值参数计算方法是准确可靠的，但文献[7-8，26]的研究结果表明：对于多负荷系统，不同的戴维南等值方法将得出不同的等值参数，因此将基于单节点负荷的经典阻抗匹配法应用于多负荷系统时仍存在一些理论问题。文献[27]列举了一个简单的3节点环网系统，通过简单的计算，发现传统的戴维南等值方法会得出错误的电压稳定性分析结果。

为解决传统戴维南等值方法所存在的问题，文献[7]提出了一种称为耦合单端口电路(coupled single-port circuit，CSPC)的电压稳定性分析方法，其主要思路是在传统的戴维南等值方法基础上，将其他负荷的耦合效应表述为一个恒定的虚拟阻抗，并接入单端口网络。文献[8]提出了通道分量变换(channel components transform，CCT)方法。CCT方法的核心思想是利用特征值分解将相互耦合的网络方程解耦为多个相互独立的通道，每个通道即是一个经典的戴维南等值电路，由此可以利用经典的阻抗匹配法来分析每个通道的电压稳定性。CCT方法为电压稳定性在线分析与监测提供了一个新的思路，但其中一个关键问题是：通道与负荷(或负荷节点)之间并不存在直接的物理对应关系，因此通道的电压稳定性并不能直接反映负荷的电压稳定性。为解决这一问题，文献[8]采用了基于贡献因子的辨识方法。

与上述研究工作的研究思路和技术途径有所不同，本文尝试利用不动点原理[28]来阐述电压稳定性问题，其核心思想是：对某一确定的时间断面，可以将网络方程表述为有关负荷节点电压向量的一个自映射非线性系统；若该系统在电压度量空间中具有唯一的不动点，则该系统在给定的时间断面是电压稳定的。由此，依据基本的不动点定理即压缩映射原理，通过简单的矩阵范数计算就可以分析、评估电力系统的电压稳定性。

1 基于不动点原理的电压稳定性分析方法

1.1 电压稳定性分析的经典模型

对于某一时间断面，电网的节点网络方程为：

(1)

式中：UG、IG分别为发电机机端电压列向量、发电机注入电流列向量；UL、IL分别为负荷节点电压列向量、负荷电流列向量；UN为联络节点电压列向量，联络节点就是既没有接发电机也没有挂接负荷的网络节点，此类节点的注入电流列向量为0；YGG、YGL、YGN分别为发电机节点与发电机节点之间的导纳、发电机节点与负荷节点之间的导纳、发电机节点与联络节点之间的导纳；YLG、YLL、YLN分别为负荷节点与发电机节点之间的导纳、负荷节点与负荷节点之间的导纳、负荷节点与联络节点之间的导纳；YNG、YNL、YNN分别为联络节点与发电机节点之间的导纳、联络节点与负荷节点之间的导纳、联络节点与联络节点之间的导纳。

基于式(1)，可以导出

UL=EG-ZLIL.

(2)

其中：

(3)

(4)

(5)

(6)

式(2)—(6)中：m为负荷的数量；yL为戴维南等值导纳；ZL为戴维南等值阻抗；zij为ZL矩阵某一元素；C为常数矩阵。

电网拓扑结构一定时，yL、yG、ZL均为定常矩阵。式(2)通常被称为多负荷系统的戴维南等值模型(multi-node coupled Thévenin equivalent model)[8]。显然，由于ZL是一个m维的满矩阵，基于单节点负荷的经典阻抗匹配法不能直接应用于多负荷系统的电压稳定性分析。

1.2 不动点原理简介

不动点原理是研究非线性方程解的存在性、唯一性以及其迭代解法的主要理论基础。对于一般的非线性自映射方程

x=f(x)，x∈Rn，

(7)

所谓的不动点就是该非线性方程的平衡点xs=f(xs)。因此，不动点理论主要是研究不动点的有无、个数、性质以及计算方法。

关于不动点定理，主要有Banach不动点定理以及Brouwer不动点定理[18]。本文主要是应用Banach不动点定理来研究电压稳定性。为避免复杂化，可将该定理简述如下：

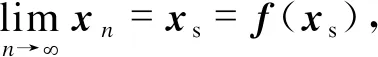
上述表达中：|·|表示Banach空间度量，可以简单化将其理解为欧氏向量范数；由于λ<1，|f(x)-f(y)|≤λ|x-y|即是所谓的压缩映射。因此，Banach不动点定理也被称为压缩映射原理，它是度量空间理论的一个重要工具，为度量空间中自映射的不动点的存在性和唯一性提供了严格的理论基础，并提供了求出这些不动点的构造性方法。

上述压缩映射在欧氏空间中可以表述为

(8)

式中：‖·‖表示矩阵的范数，具体可以取列和范数(‖·‖1)、行和范数(‖·‖)、谱范数(‖·‖2或ρ(·))。

由此，可以通过简单的数值迭代方法来阐释压缩映射原理：若式(8)成立，则下述迭代方法

(9)

必将收敛至唯一的平衡点，即不动点xs=f(xs)。式(9)是经典的不动点迭代方法，而式(8)是不动点迭代方法收敛的充要条件，也就是式(7)具有唯一不动点的充要条件。概括来说，不动点就是自映射非线性方程的稳定平衡点。

1.3 基于不动点原理的电压稳定性分析方法

为便于理解，首先从经典的戴维南等值电路(如图1所示)出发，阐述基于不动点原理的电压稳定性分析方法。图1中，Es、Zs分别戴维南等值内电势和等值阻抗，uk为k时刻的负荷母线电压，pk、qk分别为相应时刻的负荷有功、无功功率。

图1 戴维南等值电路

对图1所示的戴维南等值电路，有

(10)

式中：ik(uk)为负荷电流，通常可将其表述为有关电压变量uk的一个函数。当戴维南等值参数Es、Zs一定时，式(10)即是有关负荷节点电压uk的一个自映射非线性方程。令

(11)

则有

(12)

需要说明的是：在工程实际中，一般很难掌握负荷或负荷电流的精确数学表达式，可将式(11)所定义的y(uk)或Zk(uk)看成是负荷在某一时间断面的等值导纳或等值阻抗。

由不动点原理可知：若在一定的区间内恒有|ω(uk)|<1，即|Zs|<|Zk(uk)|，则式(10)在该区间内具有唯一的不动点，此时负荷节点电压uk将是稳定的；反之，若|ω(uk)|≥1，即|Zs|≥|Zk(uk)|，则式(10)不存在不动点，此时负荷节点电压uk将是不稳定的。

下面利用不动点原理来研究多负荷系统的电压稳定性。对于一个确定的时间断面，发电机机端电压列向量UG是确定的，因而电动势向量EG也是确定的；对一般的非线性负荷，负荷节点电流IL是有关节点电压的一个函数。在不考虑电动势EG的动态变化、只考虑负荷动态特性的情况下，可将式(2)表述为

(13)

在此情况下，有：

(14)

(15)

式(14)、(15)中：diag(·)表示对角矩阵；yeq,j(uLj)为第j个负荷在给定时间断面的等值导纳；uLj为第j个负荷节点电压；iLj(uLj)为第j个负荷节点电流；F(UL)代表与负荷电压相关的函数；Yeq(UL)为第j个负荷等值阻抗。

依据不动点原理，若负荷节点电压满足

(16)

则非线性自映射方程(13)将具有唯一的不动点，也就是负荷节点电压UL将具有唯一的稳定平衡点，因而系统是电压稳定的。式(16)是判断系统负荷是否电压稳定的直接判据。

1.4 负荷电压稳定性评估判据

下面阐述上述判据的具体计算或实施方法。理论上，式(16)中的矩阵范数可取列和范数、行和范数、谱范数，但不同的范数在计算效率方面有很大的不同。令

(17)

显然矩阵μ的计算是很简单的，它只需对常数矩阵yL进行一次性三角分解，则有

(18)

若取谱范数，则在不同的时间断面均需计算矩阵μ的特征值分解，不仅费时，而且还存在另外一个问题：取谱范数可以准确判断整个系统的电压稳定性，但很难直接判断出每个负荷的电压稳定状况，因为利用现有的特征值计算方法，无法直接确定特征值与负荷节点之间的物理对应关系。

为避免上述问题，可以采用矩阵的行和范数即‖μ‖，则有

(19)

式中γi为矩阵μ第i行绝对值之和。

依据不动点原理，若

(20)

则系统是电压稳定的。进一步，若

γi<1，i∈(1，m)，

(21)

则第i个负荷是电压稳定的。由此，可以定义各个负荷的电压稳定裕度

(22)

式(21)、(22)即是本文所提出的基于不动点原理的电压稳定性分析、评估判据。

2 相关对比分析与讨论

基于阻抗匹配类的电压稳定性分析方法，其物理概念简单，易于理解。为方便对本文所提新方法的理解，将基于不动点原理的分析方法与阻抗匹配法进行简单分析对比。

记矩阵μ、负荷阻抗矩阵ZL的特征值分解分别为

(23)

(24)

定义

(25)

则利用上述变换可将式 (2)转换为

(26)

写成解耦形式，即

(27)

式(27)即是CCT方法[8]中的通道方程，显然，它类似于图1经典的戴维南等值电路。定义通道的等值导纳

(28)

由于各通道之间是完全解耦的，可以利用经典的“阻抗模判据”方法来分析每个通道的电压稳定性，若

(29)

则该通道是电压稳定的。

依据上述定义，有：

(30)

(31)

依据矩阵范数理论，有

(32)

依据上述推导可知：矩阵∂F(UC)/∂UC与矩阵μ是相似矩阵；由于相似矩阵具有相同的特征值[29]，进一步有：

(33)

式(32)和(33)具有重要的意义，具体阐述如下。

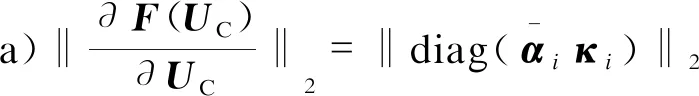
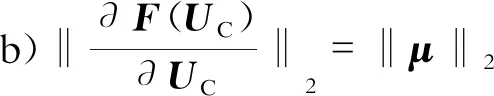
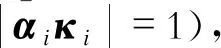
在上述基础上，若能够辨识出通道与负荷之间的对应关系，也就是辨识出特征值αi与具体负荷之间的对应关系，则多负荷系统的电压稳定性问题就迎刃而解了；然而，这个问题似乎并不简单，至少目前缺乏严格的数学工具。为解决这一问题，CCT方法采用基于贡献因子的辨识方法，具体就是计算负荷电流在通道电流中所占的比例。这里需要说明的是：由于负荷的非线性、时变特性，从理论上讲，通道(或特征值)与负荷之间的对应关系并不是一成不变的；即使上述辨识方法是正确的，但在不同的时间断面很有可能辨识出不同的对应关系。正是基于这个原因，尽管文献[8]可以通过临界通道辨识出临界负荷，但并没有通过跟踪通道的电压稳定性来实现负荷电压稳定性的在线跟踪。

下面分析本文所提出的电压稳定性判据。

假设βi，i∈(1，m)是矩阵μ的特征值，而且该特征值严格对应于第i个负荷节点，则依据Gergorin圆盘定理[27]有：

(34)

因此，若式(21)成立(即γi<1)，则必有|βi|<1，i∈(1，m)，可知该负荷电压是稳定的。这就是本文在不动点原理的基础上选择矩阵行和范数作为负荷电压稳定性判据的数学基础。

概括起来，本文所提出的基于不动点原理的电压稳定分析方法，具有比较严格的数学基础；与CCT方法相比，本文所提出的方法无需特征值分解计算，自然也无需辨识通道与负荷之间的对应关系。更重要的是，CCT方法不能实现负荷电压稳定性的连续跟踪监测，而本文所提方法完全可以用于电压稳定性的在线监测。

3 仿真测试与验证

为验证本文所提方法的有效性，利用PST (Power System Toolbox)仿真程序对其进行了仿真测试。由于CCT方法[8]不能直接跟踪负荷的电压稳定性，通过仿真测试将本文所提方法与CSPC方法[7]进行对比。

选用如图2所示的5机18节点系统作为算例系统。该系统在母线1、2、11、12和22处安装有5台发电机，所有发电机都配置有简单的励磁调节器和稳定器(power system stabilizer，PSS)；该系统共有3个负荷，分别接于母线4、14和21。母线21挂接的负荷由一台感应电动机和一部分恒阻抗负载组成；母线4和母线14处的负荷可建模为恒阻抗负荷或恒功率负荷。

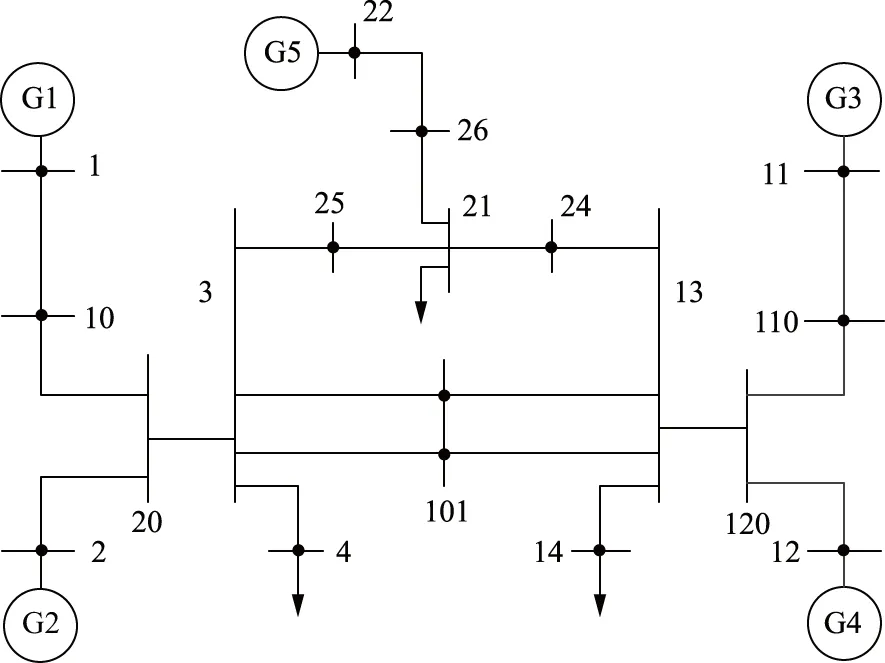
图2 测试用算例系统

仿真测试中，系统在时间t=0.2 s时母线 25处发生三相短路，经0.01 s后也就是t=0.21 s时通过开断线路3-25切除短路故障。首先将母线21处的负荷设置为60%的电动机负载和40%的恒阻抗负载。这种情况下，系统是暂态(即功角)稳定的(参见图3，其中δ21、δ31、δ41、δ51分别为发电机2、3、4、5相对发电机1的功角)，但系统是电压不稳定的(参见图4)。图5是分别使用本文所提方法以及CSPC方法对负荷电压稳定性进行跟踪监测的结果。从图5可以看出，2种分析方法的监测结果均能有效反映负荷的电压稳定或不稳定状况。

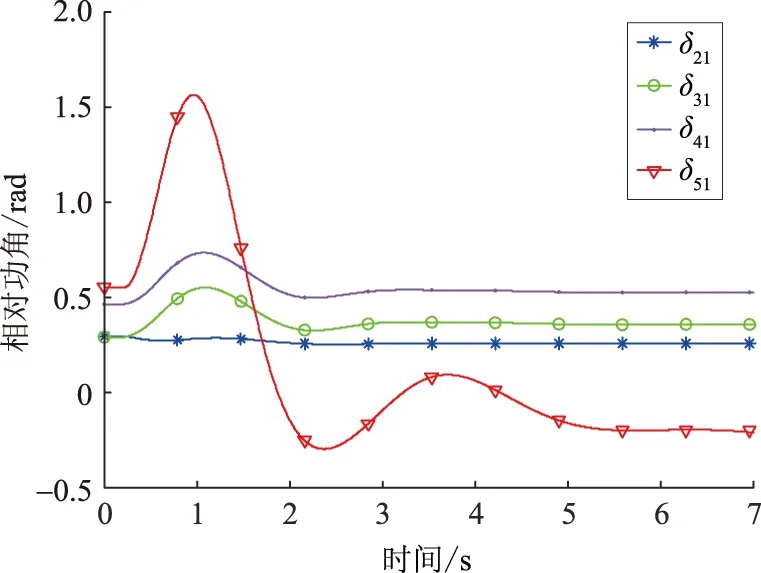
图3 功角摇摆曲线

图4 负荷电压变化曲线(不稳定)

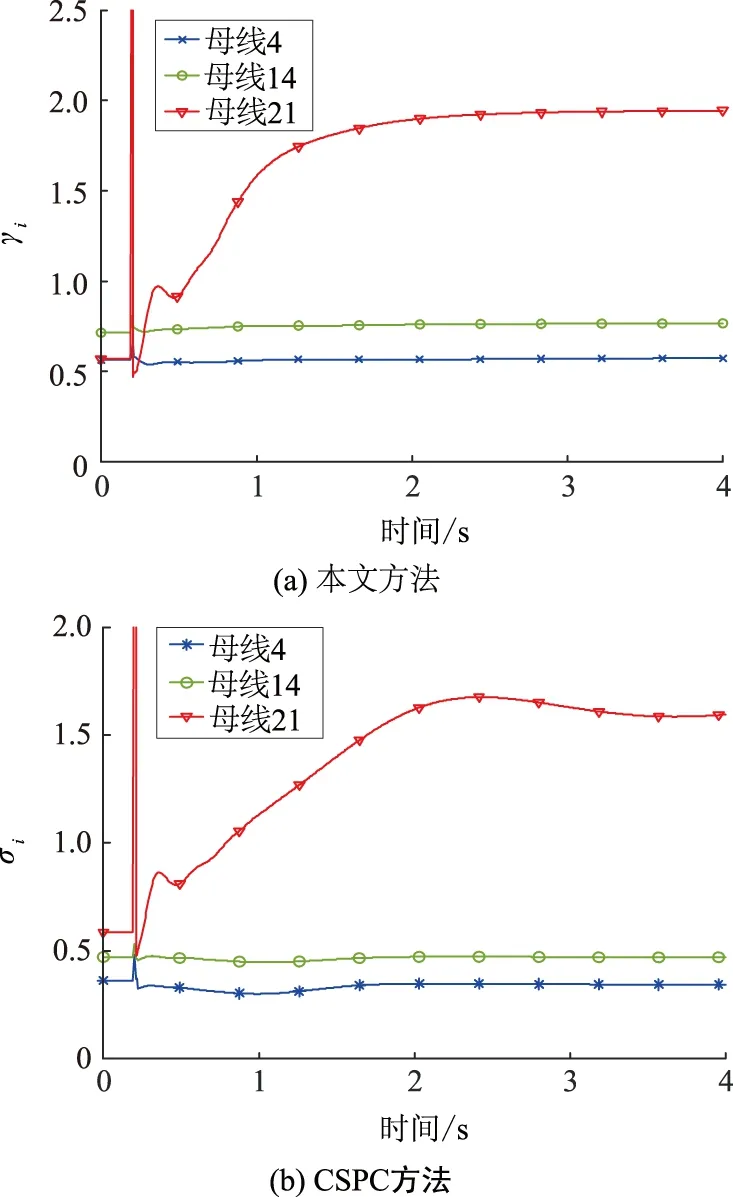
图5 负荷电压稳定性跟踪监测结果(不稳定)

将母线21处的负荷设置为40%电动机负载和60%的恒阻抗负载。这种情况下，系统既能保持功角稳定性，又能保持电压稳定性(参见图6)。图7是分别采用2种方法对负荷电压稳定性进行跟踪监测的结果。

图6 负荷电压变化曲线(稳定)

对比图7(a)与7(b)可以看出：在负荷电压稳定的情况下，基于本文方法以及基于CSPC方法所得出的电压稳定性跟踪结果在变化趋势上大致相似。上述仿真测试及对比结果说明：本文所提出的基于不动点原理的电压稳定性在线监测方法是有效的。

4 结束语

本文应用不动点理论来阐述电力系统的电压稳定性，提出了基于不动点原理的电压稳定性分析新方法及相应的判据。通过对比分析和讨论，阐述了所提新方法的合理性。

本文所提出的电压稳定性分析计算方法具有计算量少、计算快速的优点，可在线应用。仿真测试结果初步验证了该方法的有效性。

与戴维南等值类方法一样，尽管可以用于负荷电压稳定性的连续跟踪与监测，但本文所提出的基于不动点原理的分析方法没有考虑等值电动势的动态特性，仍属于静态电压稳定性分析的范畴。如何基于不动点原理来研究电力系统的动态电压稳定性，这是后续的研究课题。