基于电磁-热-流耦合场的非开挖敷设方案的海底电缆载流量计算

陆莹，范明明，郑明，王鹏宇，刘刚

(1.中国能源建设集团广东省电力设计研究院有限公司，广东 广州 510663；2.华南理工大学 电力学院，广东 广州 510641)

随着海上风电的大规模建设，海底电缆的应用也越来越广泛[1-3]。海底电缆在整个海上风电场的运行结构中同时扮演着“血管”和“神经”的角色，除了汇集、传输电能外，其内部还有光纤单元，是风电场通信及海底电缆监测信号的通道。海底电缆的敷设环境复杂，需经过多个敷设区段：海床段、滩涂段和登陆段[4-5]。海底电缆登陆处，通常采用基槽开挖或者非开挖施工，非开挖施工是指不对地面开挖沟槽而敷设电缆的工程施工工艺。广东省统筹选划了海上风电场送出海底电缆登陆点，这些登陆点多位于严格保护岸段，为降低对海岸地形地貌和生态环境的影响，多要求海底电缆登陆时采用非开挖施工工艺。这种施工工艺虽然具有对现状地面干扰小的优点，但非开挖段电缆埋深较大，导致管道内敷设的电缆散热条件较差，可能成为整条海底电缆线路的载流量瓶颈点[6]；因此，有必要对采用非开挖方式敷设处的海底电缆进行载流能力的准确评估，以判断该施工方式是否满足工程需求。

近年来，为了满足各种复杂条件下对电缆载流量准确计算的要求，有限元数值计算方法在土壤直埋、排管、沟槽、顶管、隧道等敷设条件下的电缆温度场和载流量计算中被广泛应用[7-12]；然而，以往研究大多忽略了电缆导体损耗随温度的变化特性，而直接采用IEC 60287标准计算出的电缆损耗定值作为有限元模型中的热源输入。这种简化会给电缆载流量的计算带来一定的误差，并且误差会随着计算电缆回路数的增加而显著增加[13]。

文献[14-15]同时建立了电磁-热-流耦合场模型,分别对顶管和排管内的单芯电缆的载流量进行计算；但研究的对象均为单芯电缆，未涉及3芯海底电缆(海底电缆相比陆地电缆结构更复杂，海底电缆有铅护套和铠装层等来满足复杂的海洋环境)。文献[13,16-17]分别计算了直埋和电缆沟敷设方式下35 kV 3芯海底电缆的载流量，但未对非开挖区域运行的高压3芯海底电缆的载流量进行计算。实际上，随着制造工艺的成熟，3芯110～220 kV交联聚乙烯(polyethlene，PE)绝缘海底电缆因其占海面积小、传输容量大而拥有更为广泛的应用。

本文利用Comsol Multiphysics有限元分析软件，以实际工程中的交流3芯海底电缆为例，搭建基于电磁场、流体场和热场的3物理场的耦合模型。该模型通过求解电磁场计算海底电缆线芯导体损耗、金属护套损耗和铠装损耗，同时考虑了线芯导体电阻率随温度的变化关系。利用模型对比计算了某地非开挖敷设方式下220 kV双回路海底电缆采用顶管和排管方案的载流量，并分析了改变管道材质和采用充水方案对海底电缆载流量的影响情况，为海底电缆选型及登陆处施工方案的选择提供参考。

1 实际海底电缆线路敷设案例

以某沿海地区的海底电缆输电工程为例，该工程中海底电缆线路的登陆段要穿越严格保护岸段，此段采用非开挖的顶管或者定向钻的施工方式，将2回220 kV海底电缆穿过道路输送到陆上集控中心，敷设方式如图1所示。根据主接线型式，每回220 kV海底电缆要求传输容量为203.5 MW，额定载流量为563 A。

图1 海底电缆登陆段敷设方式示意图

该工程采用型号为HYJQF 41-F-127 kV/220 kV的3芯3×500 mm2海底电缆作为送出海底电缆。由于导体屏蔽和绝缘屏蔽层厚度小，其热物性参数与绝缘层接近，为简化计算，海底电缆的导体屏蔽层和绝缘屏蔽层均视作绝缘层处理，海底电缆具体结构参数见表1[18]。

表1 海底电缆的结构参数

本工程考虑2种方案：第一种方案是采用水泥顶管施工方案，顶管内径为1.50 m，壁厚为0.15 m，双回路海底电缆敷设于顶管内，2个回路海底电缆中心距离为0.6 m，顶管内海底电缆布置如图2(a)所示；第二种方案是采用定向钻施工方案，利用内径为0.724 m、壁厚为0.038 m的PE排管敷设海底电缆，2个排管中心距离为2.4 m，排管内海底电缆布置如图2(b)所示。本文重点对非开挖方式下双回路海底电缆在水泥顶管和定向钻PE排管这2种情况下的载流量进行计算分析。

图2 海底电缆布置图

2 非开挖敷设海底电缆的多物理场耦合模型

2.1 理论基础

对于采用非开挖敷设方式的海底电缆，顶管和排管内的海底电缆是唯一热源，其发热包括线芯导体通电产生的焦耳热、绝缘层介质损耗、金属护套损耗和铠装层损耗。海底电缆的散热包括海底电缆和周围土壤等固体介质的热传导、管道内海底电缆外表面与管道内壁之间空气的自然对流和管道内海底电缆外表面与管道内壁间的热辐射3种方式。

为了提高仿真模型的计算效率，现作出如下假设：

a)相比较于海底电缆的横截面，其长度可认为无限长，本例中非开挖段长为57 m，在不考虑电缆敷设时扭曲的情况下，将计算问题简化为二维平面问题。

b)电缆的线芯导体的电导率σ随温度发生变化，即

式中：ρ20为线芯导体在温度为 20 ℃时的电阻率，Ω·m;α20为线芯导体在温度为 20 ℃时的电阻温度系数，K-1；T为线芯导体的温度，K；T20=293.15 K。

2.2 物理场控制方程

2.2.1 热传导微分方程

稳态下有热源区域(如海底电缆导体、金属护套和铠装层)的热传导控制方式为

·(λT)+qv=0.

式中：λ为介质导热系数；qv为介质单位体积发热率。无热源区域(如海底电缆其他层、土壤等)的热传导控制方程为

·(λT)=0.

2.2.2 热对流微分方程

顶管内的空气主要涉及自然对流散热，通过计算瑞利数Ra大于109，故顶管内的空气流动形态预测为湍流。本模型采用标准k-ε湍流模型(k为单位质量流体湍流脉动动能，ε为k的耗散率)对流体的传热和流动进行描述。排管内空间更小，通过计算瑞利数Ra小于109，其空气流动形态预测为层流。管内空气自然对流连续性方程、流体动量方程和能量方程分别为：

式中:u、v分别为点(x,y)处空气流速在x、y轴方向的分量，m /s;ρ为流体的密度，kg/m3;p为流场的压力标量，Pa;η为动力黏度，Pa·s;β为流体的体积膨胀系数,K-1;θ为重力加速度与x轴的夹角;Tr为流体参考温度，℃;k1为流体的导热系数，W /(m·K)。

2.2.3 热辐射微分方程

海底电缆外表面和顶管内表面之间存在热辐射，传热为

Qi=σSεiFijAi(Ti2+Tj2)(Ti+Tj)(Ti-Tj).

式中:Qi为面单元i的传热率，J/m2；S是Stefan-Bolzman常数；εi为面单元i的有效热辐射率;Fij为面单元i与j的角系数；Ai为面单元i的面积;Ti和Tj为面单元i和j的绝对温度值，K。

2.3 热源计算

在进行模型求解时不考虑三相电流的不平衡带来的影响，对3芯海底电缆的各线芯导体施加幅值相同、相位相差120o的电流值。海底电缆内部金属护套采取两端接地方式，不产生环流。

海底电缆导体、金属护套、铠装层的矢量区域的电磁损耗计算式为：

式中：μ为各材料的磁导率，均设为4×10-7H/m；ω为50 Hz工频对应的角频率，rad/s；A为各区域的矢量磁位，Wb/m；Js为导体总电流密度，即源电流密度；P为线芯导体、金属护套或铠装层的单位长度电磁损耗分别为A和Js导数。

每相中单位长度的绝缘损耗

Wd=ωCU02tgδ.

式中：U0为海底电缆对地电压(相电压),V；C为单位长度电缆电容，F/m；tgδ为电源系统在工作温度下的绝缘损耗因数。

2.4 边界条件

为了保证多物理场耦合模型的计算效率和准确性，将其转变为等效闭域场进行求解。现设定顶管和排管中的海底电缆埋设深度均为10 m，底部20 m处为求解域的下边界，距离管壁左右两侧 20 m处为求解域左右边界，且：

深层土壤边界为第1类边界条件Γ1，满足

T|Γ1=φ(x,y).

左右土壤边界为第2类边界条件Γ2，满足

T|Γ2=f(x,y,t).

顶管、排管上方的地表为第3类边界条件Γ3，满足

式中：φ(x,y)、f(x,y,t)分别为已知温度的求解域对应的温度函数;g(x,y,t)为边界上热流密度向量函数；n为导体芯数。2种非开挖敷设方式的几何模型如图3所示，海底电缆的敷设环境的参数见表2。

图3 2种敷设方案的二维几何模型

表2 海底电缆敷设环境的参数

3 计算结果及分析

3.1 水泥顶管敷设方案

采用顶管施工方案，在海底电缆线芯导体稳定通入567 A电流的条件下，双回路海底电缆的电磁损耗分布、空气流速场和温度场如图4所示。

从图4(a)可以看出：海底电缆热损耗主要由线芯产生，因趋肤效应，线芯边缘处的热损耗最大。利用表面积分得到单回路海底电缆线芯导体、金属护套、铠装的电磁损耗密度分别为41.130 W/m、9.268 W/m、7.536 W/m,金属护套和铠装的涡流损耗较大。从图4(b)可以看出:海底电缆的正上方和靠近海底电缆管壁处空气流速最大，其中最大的空气流速为0.13 m/s，其他大部分区域的空气流速较小，这说明海底电缆产生的热量很大一部分通过两侧的顶管金属壁向外界土壤扩散。从图4(c)可以看出:温度场由于海底电缆线芯导体产生的焦耳热为主要热源，海底电缆的最高温度出现在线芯导体区域，为90.1 ℃，且温度从线芯导体区域向外逐渐降低，海底电缆外表面温度为67 ℃。

图4 水泥顶管施工方案下的电磁损耗分布、管内空气流速场和温度场分布

3.2 定向钻PE排管敷设方案

采用定向钻施工方案，在排管内的海底电缆线芯导体中通入557 A电流的条件下，此时海底电缆的温度场、空气流速场分布如图5所示。由图5可知：海底电缆正上方和左右管壁的空气流速较高，最大的空气流速达到0.19 m/s；海底电缆正上方的部分空气温度较高，因为空气受热向上流动，将之前上方温度较低的空气挤走了。由于间隔距离较远，2个排管之间土壤的温度并没有明显的升高，此时采用排管敷设方式的海底电缆载流量为 557 A。PE排管相比水泥顶管的载流量更低，这是由于PE排管的导热系数小，而且排管内的空间更小导致热量不易散失。

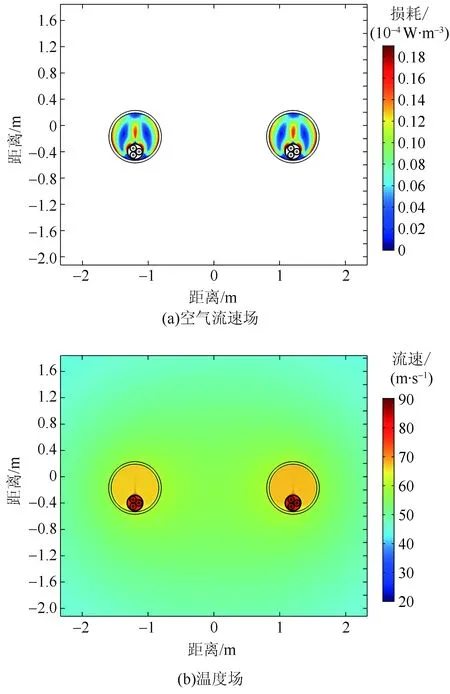
图5 定向钻PE排管施工方案下排管内空气流速场、温度场的分布

在相同的环境条件下，顶管敷设方案比排管的载流量高10 A，差距很小；虽然顶管内空间更大，但由于容纳2个回路海底电缆，电磁损耗增加，空气的热阻较大，使顶管内的温度升高，此时采用排管方案的载流量为557 A，不能满足本项目的输送要求。

由图6所示，当只有1个回路海底电缆线路运行时，水泥顶管敷设方式下的载流量为678 A；所以，当1个回路海底电缆线路故障的时候，采用顶管敷设方案海底电缆允许输送的容量更大。

图6 1个回路海底电缆运行时的温度场分布

3.3 载流量提升方法

交流电缆的允许连续载流量可以根据IEC 60287-1-1中载流量计算的经验式进行计算[19]，即

式中：I为电缆允许连续电流，A；Θc为导体温度，K；Θa为电缆所在环境温度，K；Wd为导体绝缘单位长的介电损耗，W/m；T1为导体与护套之间的热阻，(K·m)/W ；T2为护套与铠装之间衬层的热阻，(K·m)/W ；T3为电缆外护层的热阻，(K·m)/W；T4为电缆表面与周围介质之间的热阻，(K·m)/W；R为运行温度下导体交流电阻，Ω/km；λ1为金属套的损耗与导体损耗之比；λ2为铠装层损耗与导体损耗之比。

计算载流量的参数时，电缆本体相关的参数与敷设方式无关，不同的敷设方式在计算载流量的过程中最大的区别是电缆与周围介质之间的热阻T4。T4越大，该敷设方式下海底电缆的允许载流量就越小。采用有效措施降低T4，从而达到提升载流量的效果[20]。

3.3.1 顶管敷设方案载流量提升方法

海底电缆可以长期浸泡在水中，有限空间内水的自然对流效果也能加快热量的传递，因此考虑该非开挖段海底电缆利用水的自然对流带走海底电缆的热量，从而达到改善海底电缆散热环境、提升载流量的效果[21]。在顶管段充满水，建立二维电磁-热-流耦合的数学模型，在海底电缆线芯导体中通入613 A电流，顶管内的最高温度达到90.1 ℃，内部流速和温度场分布如图7示。

图7 充水顶管流速场、温度场的分布

由图7可知：顶管内水的流速较小，最大水流速为0.006 8 m/s，这是由于靠近海底电缆处的水受热后密度变小引起顶管内水的自然对流，水的热膨胀系数小于空气，而动力粘度和密度远远大于空气，使得水的流速降低。顶管内海底电缆上方和两侧管壁处的水流速较快，这说明类似于空气，海底电缆产生的热量一部分通过两侧的管壁向外界土壤扩散。顶管内的水吸收了大量的热量，并通过顶管壁向外界土壤扩散，管内水的温度分布趋于均匀，这是因为管内水的自然对流使得水的等效热阻很小。

3.3.2 定向钻敷设方案载流量提升方法

定向钻敷设方案载流量提升方法包括：

a)采用热阻系数较低的管道材质。如金属管道代替PE管道，由于金属管道热阻极小，从而降低排管本身的热阻。通过将PE排管置换成相同尺寸的钢管道建立仿真模型，得到其载流量为603 A。

b)在管道中充水，利用水的良好导热性，带走海底电缆的热量，从而达到改善海底电缆散热环境、提升载流量的效果。分别在PE排管和钢管道内充水建立仿真模型，得到其载流量分别为625 A和652 A。排管采用钢管道，充水时的内部流速场和温度场如图8所示。

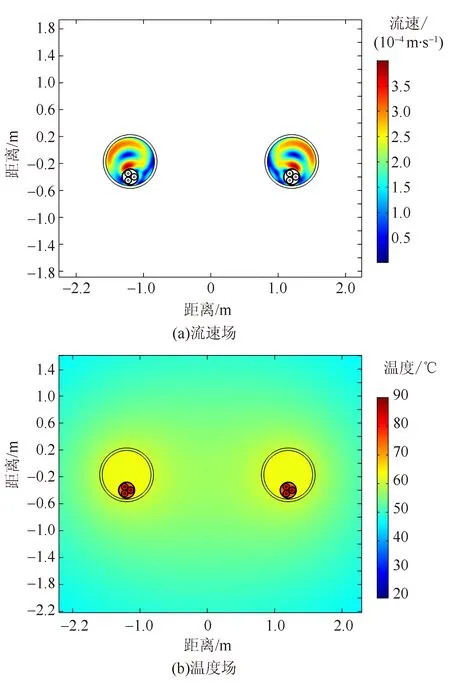
图8 充水钢管道内的流速场、温度场的分布

顶管和排管敷设方式下海底电缆载流量的提升效果对比见表3。

表3 2种敷设方式下载流量的提升效果对比

由表4可知：在水泥顶管内充水可以提升载流量达到8%；在排管敷设方式下，采用PE排管充水和采用钢管道提升载流量分别为12%和8%；当排管敷设方式同时采用钢管道和充水的情况下载流量提升了17%，提升效果显著。

4 结束语

本文计算了220 kV 3芯交联PE绝缘3×500 mm2海底电缆登陆处，双回路海底电缆在水泥顶管和定向钻PE排管2种情况下的载流量。基于文章第2.1节的2点假设，建立了二维电磁-热-流耦合场仿真模型，通过分析发现:在海底电缆埋深均为10 m的情况下，采用水泥顶管方案能满足工程输送容量的要求，采用PE排管方案的载流量略低于额定容量，2种敷设方案的载流量差距很小。当1回海底电缆故障的时候，采用水泥顶管方案海底电缆允许输送的载流量更大，比采用PE排管的方案载流量高21.7%。

针对常用的2种非开挖敷设方案，提出了适用于顶管和排管敷设的载流量提升方法。采用水泥顶管敷设方案时，可通过给顶管内充水达到进一步提升载流量的效果，在相同的环境条件下，可提高载流量8%；采用排管敷设时，可通过改变管道材质、管道内充水的方法达到提升载流量的效果，在相同的环境条件下，采用钢管道和充水分别可提高载流量8%和12%。本文所采用的双回路、220 kV、电缆截面为3×500 mm2的海底电缆，在国内海上风电项目中普遍采用，所选取的案例具有一定的普遍性，相关结论可以为海上风电项目海底电缆选型及登陆处施工方案的选择提供参考。