适用于电力计量的自动导引运输车控制系统研究
蔡杨华,谭金,王冠
(1.广东电网有限责任公司电力科学研究院,广东 广州 510080;2.广东电科院能源技术有限责任公司,广东 广州 510080)
现有计量检定中心库前区多采用人工装卸货方式,存在工作效率低、错误率高、管理混乱等问题。当库前区使用自动装卸装置时,需实现表计周转箱从立体仓库往返配送车辆的运输、定位、摆放等过程的自动化[1-2]。受到库前区货物堆放杂多、环境干扰大、配送车辆规格不一等因素限制,现有的自动装卸技术只能实现特定规格车厢的装卸,难以满足无人化库前区的需求。目前,国外自动装卸货系统主要是通过对自有物流的车厢、月台以及各衔接环节实施标准化设计制造来实现货物的自动装卸。我国采用第三方物流,车厢大多未进行标准化设计或改造,无法使用现有国外成熟的自动装卸方案,同时国内对适于现有国情的自动装卸系统也鲜有研究;因此,开展库前区自动装卸装置的研究对响应国家智能化制造策略和提高计量检定中心智能化及无人化运行水平意义重大[3]。广东电网电能计量检定中心旨在建设成国内技术与管理水平领先的计量检测单位,实现计量检测的标准化与自动化,满足市场改革形势下广东“十三五”及“十四五”期间电能计量设备大规模推广的检定需求[4]。计量库前作业区作为计量检定自动化的起始区域,是提高广东电网计量检定中心自动化出入库作业效率极其重要的一个环节。计量库前区的主体为自动导引运输车(automated guided vehicle,AGV),实现电能计量周转箱垛的自动存入、自动取出及存储等功能。AGV的核心之一便是稳定准确的控制系统;为此,本文对库前区自动装卸装置的控制系统进行了建模和仿真,利用运动学模型和物理模型的建立、轨迹规划控制算法的仿真,验证现实运行过程工况的参数及方法,为智能匹配作业环境和实现对计量周装箱自动装卸的控制策略提供基础。
1 控制系统与仿真流程
AGV的控制系统需满足智能AGV的运动及装卸物料控制要求[5-7],具体内容如下:自动装卸货AGV在控制系统作用下将1垛周转箱自动装车及卸车,其涉及到智能判别货物及车厢位置、精确的路径规划和准确的停车位置等技术[8-10]。依据表1相应的需求进行控制算法及系统设计,并对AGV控制系统进行仿真模拟,根据仿真过程的表现及参数来验证控制系统设计的合理性,最终优化改进控制算法及控制方案。
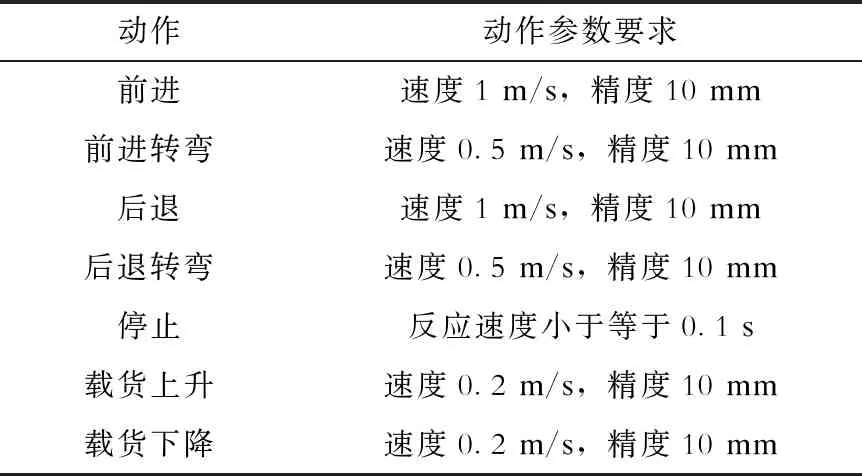
表1 控制功能主要需求
控制系统在设计过程中涉及到了车体的运动学及动力学问题[11],对其进行仿真分析可保证所设计控制系统的可靠性和稳定性;此外,轨迹规划及跟踪控制的算法也需经过仿真验证可行之后才能作为实际车体调试的最终输入。
本文主要使用MATLAB对设计的控制算法进行仿真模拟,用以验证控制系统的可行性及准确度。使用机器人运动仿真V-rep软件来模拟AGV的整体运行情况,并应用MATLAB控制程序对V-rep物理模型进行运动控制,有效模拟自动装卸货AGV的现实工况。
2 系统模型建立
2.1 运动学模型建立
为方便分析作如下假设:①车体质心位于左右对称中心处; ②两后轮关于中心线对称分布;③车体运行在平稳地面且在Z方向不考虑移动,X和Y方向上不考虑翻转;④车体为刚体[12]。激光雷达安装在两支撑轮的连线中心,如图1所示。以激光雷达位置点C为中心建立瞬时惯性坐标系XCY(车体坐标系),规定逆时针转角和角速度为正。车体在转向过程中能够平稳转动的条件是:每个车轮同时围绕一个速度瞬心做圆周运动(如图1所示),车体以左右车轮延长线上的某一点O以角速度ω转动,此时底盘运动过程中无侧滑。图1中,VA为舵轮在A点的线速度,ωA为舵轮在A点的角速度,R为舵轮半径,φ为舵轮转角,ω为车体角速度,L为前轮轴心与后轮轴心线的间距,VX为跟踪点沿X轴方向的速度,VY为跟踪点沿Y轴方向的速度,X为跟踪点的横坐标,Y为跟踪点的纵坐标。

图1 车体运动分析
假设舵轮在前进方向不打滑,只作纯滚动,即:
VA=ωAR.
(1)
ω=ωARsinφ/L.
(2)
车架激光雷达位置处的运动方程为:
VX=ωL-VAsinφ=0.
(3)
VY=VAcosφ=ωARcosφ.
(4)
图2为以地图原点位置为中心建立瞬时惯性坐标系XOY,规定逆时针转角和角速度为正,则在地图坐标系下有以下关系:
(5)
(6)
(7)
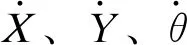

图2 车体运动分析
AGV在运动过程中,初始位姿状态可用[XYθ]T表示,目标位姿状态可用[X1Y1θ1]T表示,其中位姿误差为[XeYeθe]T。
算法验证过程采用小车的运动学模型来计算模拟实际运行过程中小车的位置坐标,考虑到实际情况的各种干扰,在运算结果中加入高斯分布的误差值进行模拟[13-15]。
对式(5)—(7)进行离散化便于计算机进行处理,Ts表示采样时间间隔,离散结果如下:
Xn+1=Xn+TsωARcosφncosθn,n=1,2,….
(8)
Yn+1=Yn+TsωARcosφnsinθn.
(9)
θn+1=θn+TsωARsinφn/L.
(10)
扰动信号采用高斯噪声,由于采样时间间隔很小,所以噪声数量级为毫米级。
2.2 物理模型建立
本文使用具有真实物理引擎的仿真软件V-rep对AGV的物理模型进行运动学和动力学仿真,检查控制算法的正确性,依据算法规划有效的路径[16],可有效避免小车在实际运行过程中不按照预想轨迹运行甚至撞车等异常情况。仿真前首先需要在V-rep中建立AGV小车的物理抽象模型,主要功能是模拟小车的各个运动关节,如图3(a)所示。主要功能模拟如下:①车体——以立方体代替,设置为基体,并设置其质量、转动惯量等参数。②从动轮——从动轮数量为2个,以圆柱体代替,设置其质量和转动惯量等物理参数。③从动关节——从动关节数量为2个,连接基体与2个从动轮,设置为从动关节。④舵轮转架——以圆盘代替,设置其质量和转动惯量等物理参数。⑤转向关节——使能,并设置最大速度,使用其位置控制功能。⑥舵轮——以圆柱体代替,设置其质量和转动惯量等物理参数。⑦行走关节——使能,设置最大加速度,使用其速度控制功能。⑧货叉——以立方体代替,并设置其质量和转动惯量等物理参数。⑨位移关节——使能,并设置最大速度,使用其位置控制功能。
对AGV小车进行外形建模,因为仿真的需求,外形模型主要以提取特征点、满足关键的运动关节处为主,整体的模型效果如图3(b)所示。
将外观模型导入V-rep仿真软件中,并将相关部件与抽象的物理模型进行融合,得到在仿真软件中可控的、具有物理参数的真实AGV模型,如图3(c)所示。建立的AGV小车物理模型有3个控制电机作为输入控制窗口,分别控制转向关节、行走关节、货叉位移关节。
2.3 运行场景搭建
为了真实模拟现实自动装卸货的运行过程,本文在仿真软件V-rep中搭建了AGV装卸货的运行环境,如图4所示。运行环境中实际存在的物理实体为登车桥、车厢和货物,其中车厢和登车桥在环境中是静止的,货物则设置成90 kg质量以便模拟被AGV小车货叉装卸和搬运。
在搭建的环境中还设置了AGV运行过程中的各个站点,在现实运行环境中这些站点是不会标记在地面上的,只是存储在地图中与AGV系统进行比对。在仿真环境中为了得到更好的显示效果,将这些站点以圆盘的形式显示在搭建环境中,以便在仿真过程中比对站点的跟踪效果;此外,为了显示货叉取货的场景,仿真中在AGV车尾添加了相机传感器,可将车后的场景实时显示在监视画面上。至此已完成了仿真场景的搭建,其中设置的站点是可按照实际运行环境进行添加及变更的。
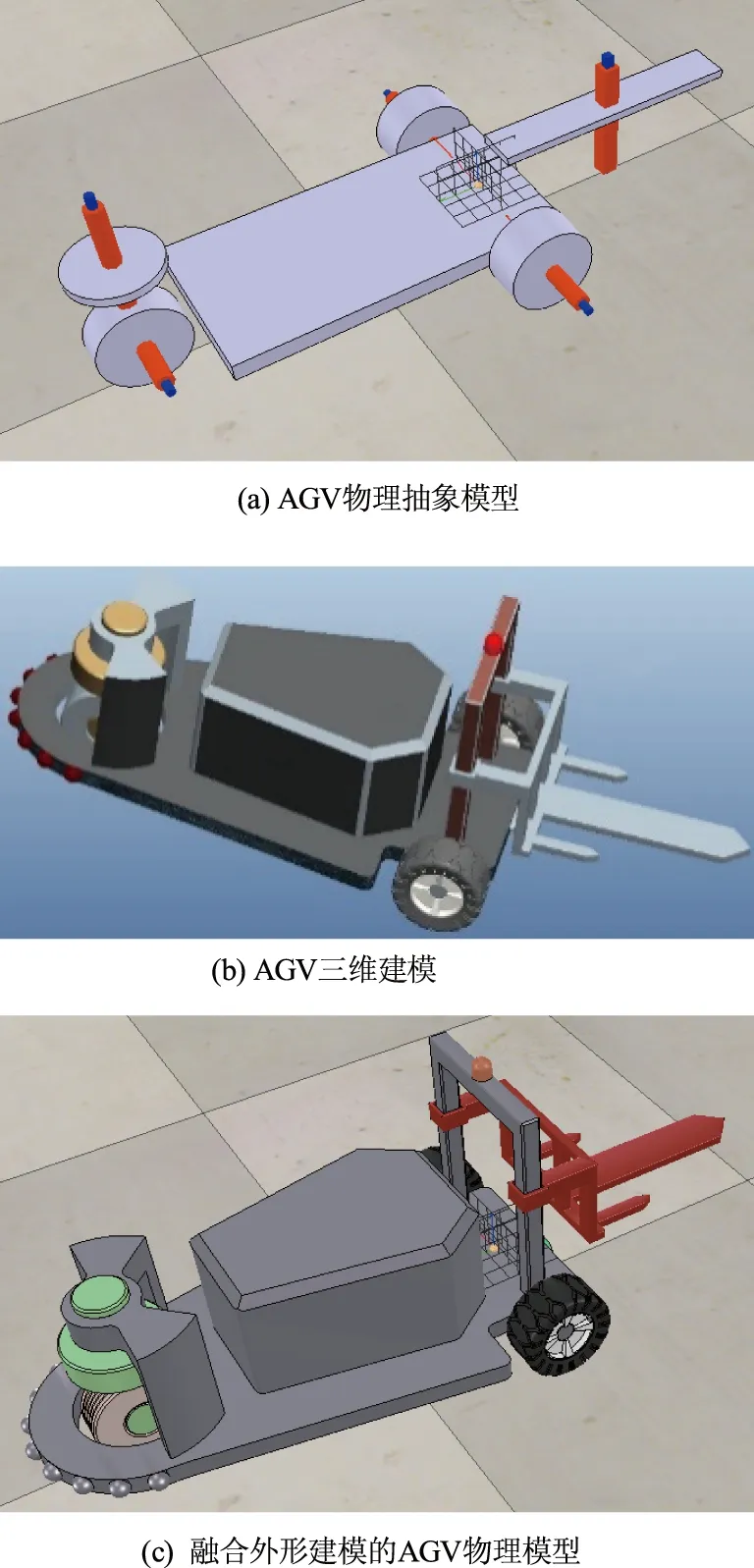
图3 AGV模型
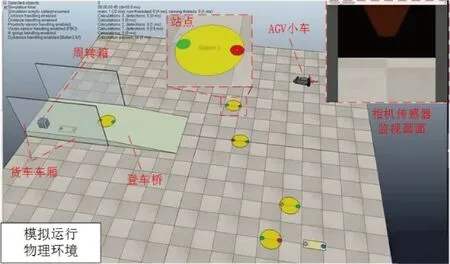
图4 模拟运行物理环境
3 轨迹规划算法仿真
3.1 直线行驶路径仿真
直线行驶要求实时规划舵轮与终点的直线路径,每一个采样周期计算能使舵轮朝向终点直线前进的舵轮转角和剩余行驶距离[17],并且输出控制,具体步骤如下:①获取上一周期位姿信息及舵轮转角,并计算本周期小车的位姿;②利用本周期位置坐标和终点坐标计算剩余行驶距离;③计算舵轮位置坐标;④利用舵轮位置和终点位置构成直线和车体的夹角计算本周期舵轮转角,具体计算式如下:
(11)
(12)
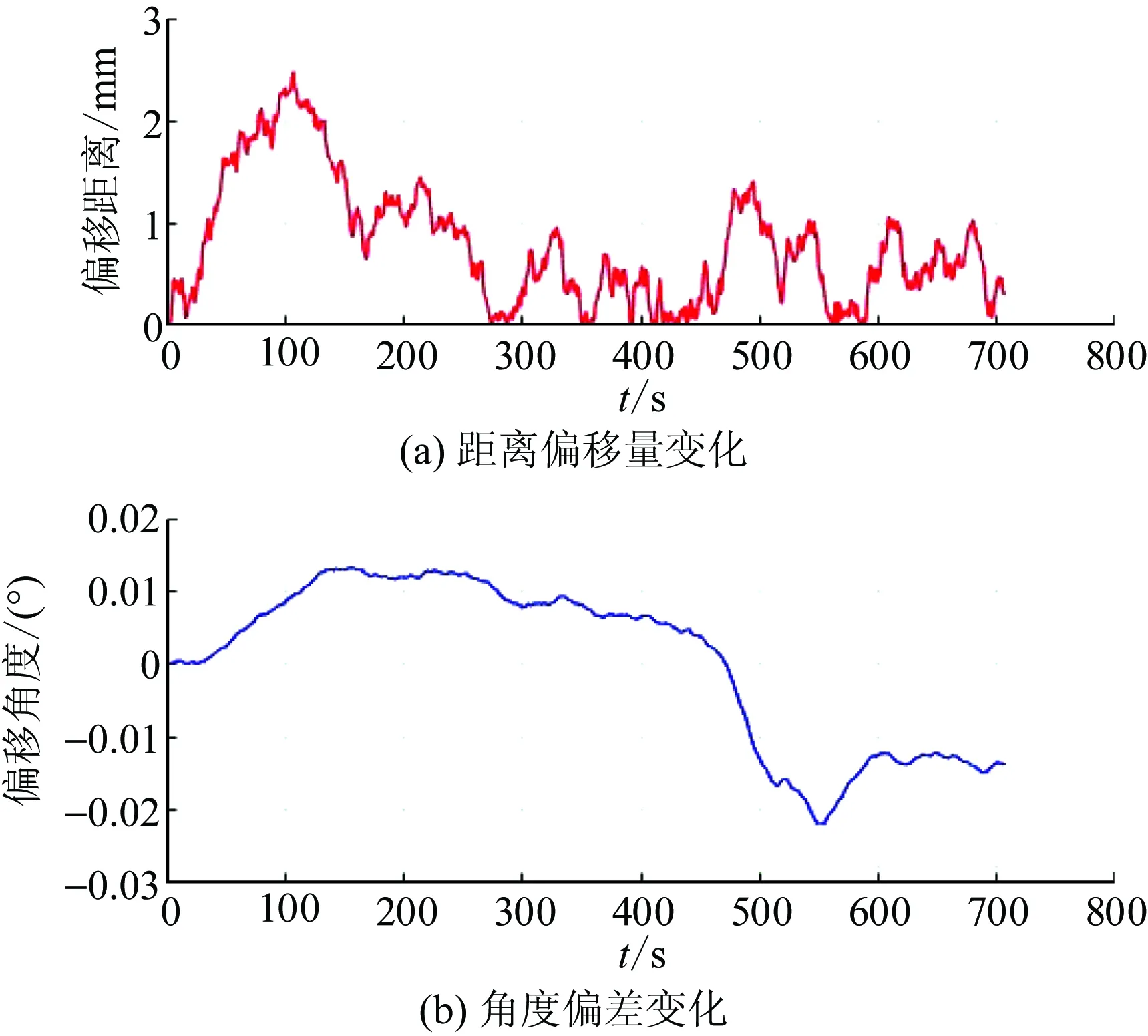
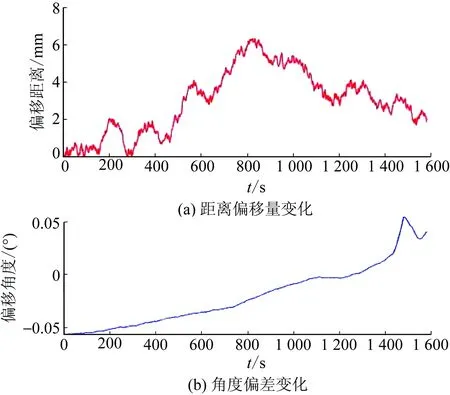
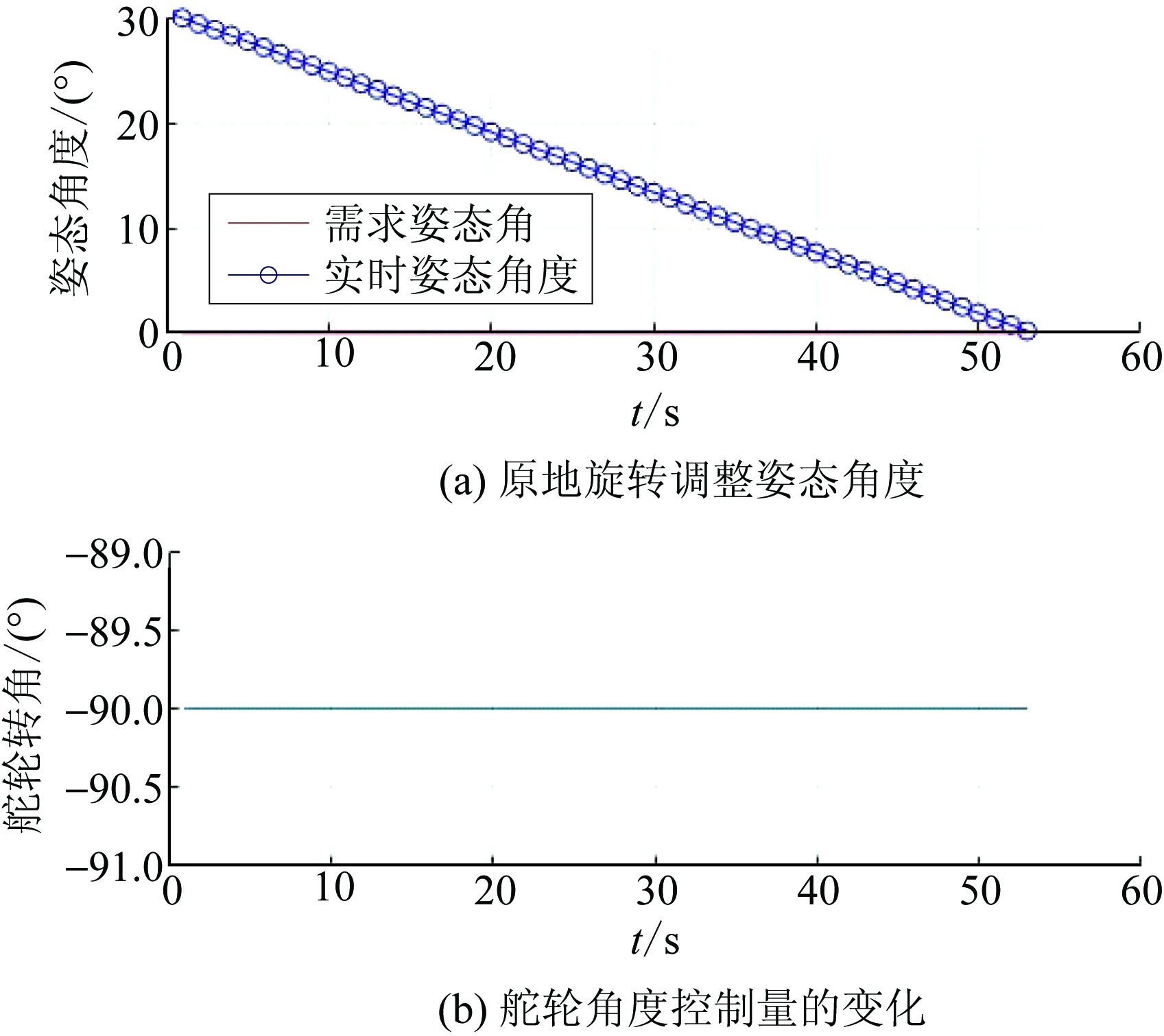
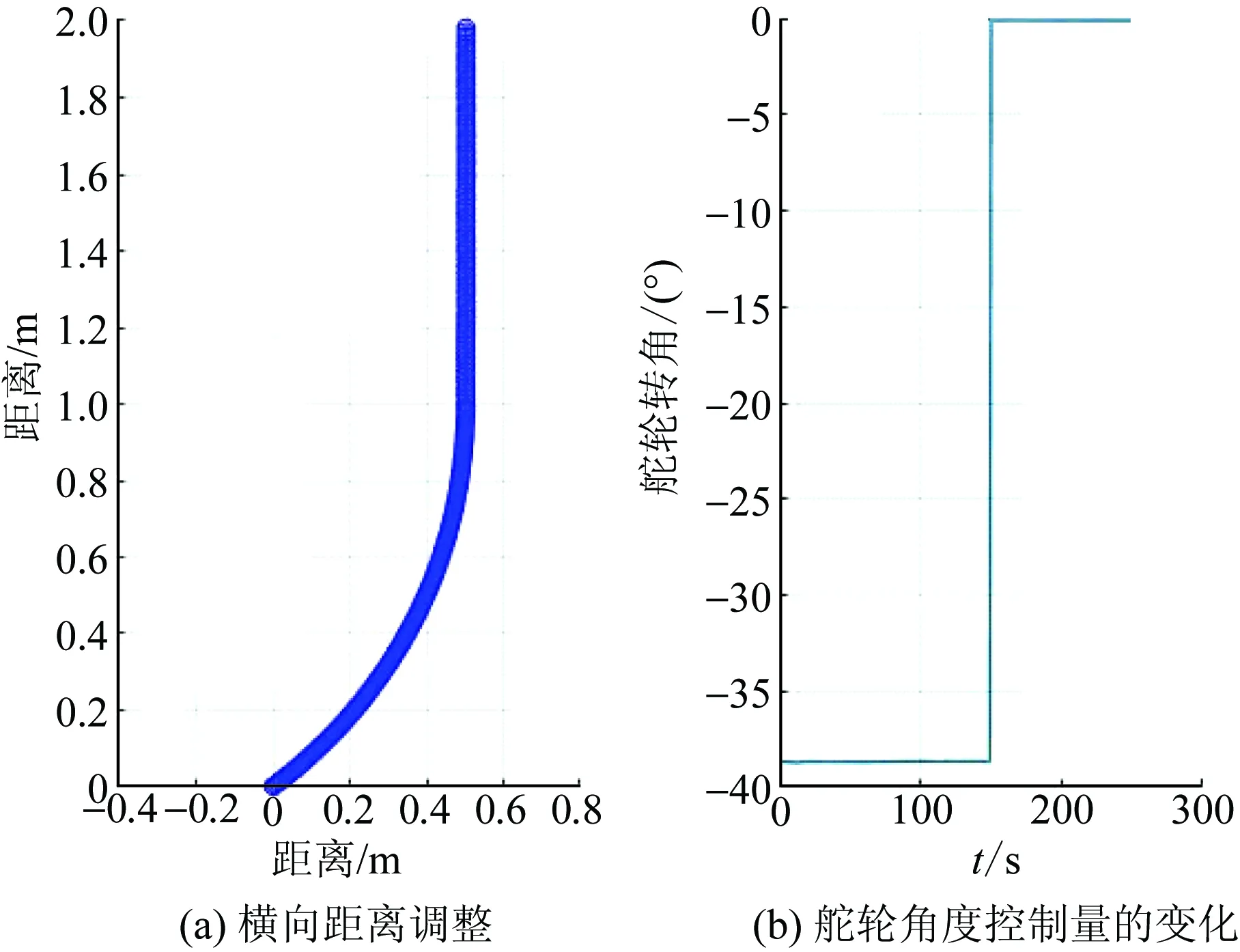
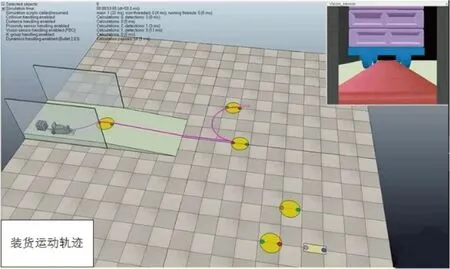
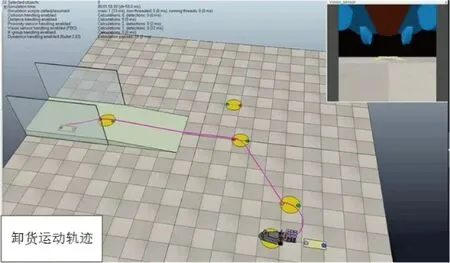
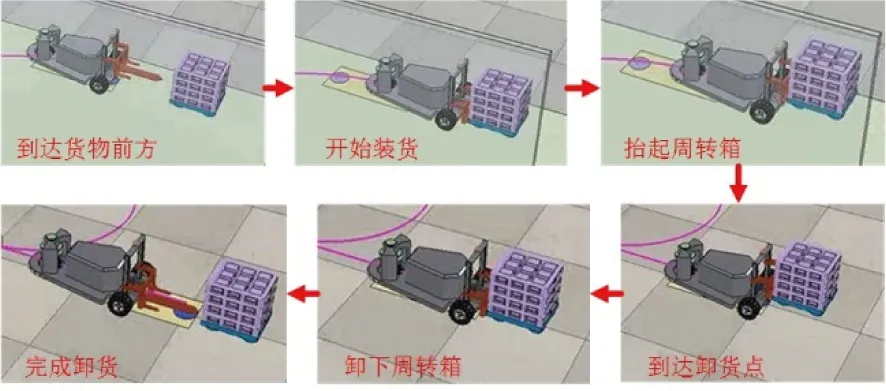
φt=0,S (13) (14) (15) 式中:S为跟踪点与终点的距离;(xt,yt)为t时跟踪点位置坐标;(xe,ye)为终点位置坐标;φt为舵轮t时转角;α为跟踪点和终点连线与跟踪直线的夹角;θt为t时姿态车体中心线与横坐标的夹角;h为跟踪点与跟踪直线的距离;(x0,y0)为起始点位置坐标。 直线跟踪算法仿真得出的结果如图5所示。从图5中可以看出:该算法可很好地跟踪确定直线路径,小车实际行走路径与理论路径非常接近,并且跟踪过程中舵轮转角控制量波动能保持在0.05°以内,对于直线行走控制系统来说较为稳定。通过计算可以得到跟踪过程中距离偏离量的变化和姿态角度变化的结果,如图6所示。从图6中可知:直线跟踪路径偏移量最大为 3 mm,满足控制设计要求(10 mm);姿态角度偏差最大为0.02°,满足行车要求。 实时规划雷达跟踪点与终点的劣弧路径,每一个采样周期计算雷达点到终点行走固定圆弧的舵轮转角和剩余行驶距离,并输出控制[18]。具体步骤如下:①获取上一周期位姿信息及舵轮转角,并计算本周期小车的位姿;②利用本周期位置坐标和终点坐标计算剩余行驶距离;③计算当前跟踪点与终点构成圆弧的割线角、圆弧半径以及圆心角;④利用舵轮与两后轮共心转动的特点并结合圆心位置计算本周期舵轮转角,具体计算式如下: 图5 直线轨迹仿真 图6 跟踪偏差 S=γR. (16) (17) γ=β-θt. (18) (19) (20) 式中:γ为跟踪点与终点规划圆弧的圆心半角;β为跟踪点与终点连线与横坐标轴的夹角。 圆弧跟踪算法仿真结果如图7所示。由图7可看出:该算法可很好地跟踪确定圆弧路径,小车实际行走路径与理论路径非常接近,并且跟踪过程中舵轮转角控制量波动较小,系统较为稳定,只有在起始阶段舵轮角有阶跃输入。通过计算可以得到跟踪过程中距离偏离量的变化和姿态角度变化,结果如图8所示。由图8可知:路径偏移量最大为 6 mm,满足控制系统路径偏移量最大为10 mm的设计要求;姿态角度偏差最大为0.05°,AGV运行稳定性良好。 图7 圆弧轨迹跟踪 图8 圆弧跟踪偏差 原地旋转比较简单,只要将舵轮角度调制90°或-90°进行运行即可,运行时检测姿态角的偏差量,达到误差范围内时停止。需要注意的是,原地旋转运动时,车速是很低的。AGV原地旋转从30°调整到0°仿真结果如图9所示。 图9 原地旋转运行 AGV在装卸货时需要调整自身方向使其可以准确地取放货物,由于取货时AGV在车厢内部,其行走路线规划不合理就会和车厢发生碰撞[19-20],所以本文所用的控制方法是在起始位置首先调整好角度使AGV在逼近目标位置时自身状态是偏向车厢内侧的,以防与车厢碰撞。具体步骤如下:①根据相机反馈货物位置进行初始姿态角度的计算;②依据计算的初始位姿角度对AGV进行原地旋转调整到所需角度;③AGV进行圆弧轨迹规划跟踪,逼近目标的位置;④进入取货位置后,AGV进行一段缓慢的直线运行后插货。图10为装卸货时方向调整的仿真结果。 图10 装卸货路径调整 从图10可以看出:在自动装卸货AGV对正货物调整路径时,控制算法可以实现10 mm精度以内的跟踪控制,系统的控制量转角也相对稳定。 对AGV小车物理模型和运行环境进行控制运行仿真。仿真过程中,AGV小车的实时坐标会显示在窗口界面中,小车的运行轨迹也在仿真环境中进行了显示,此外对相机的视频数据也进行了实时显示,如图11、12所示。仿真的主要内容是:利用MATLAB的轨迹跟踪控制算法的代码不停地计算舵轮转角和转速2个控制量,然后传输至V-rep软件中的关节电机模型中,以此控制AGV小车进行运动。在仿真运行过程中既要控制小车运动,也要对货叉的运动进行控制仿真,在AGV小车运行到装卸货位置时,货叉电机会受到控制信号进行位置变动,以此来完成货物的取放,如图13所示。 图11 AGV装货运动轨迹 图12 AGV卸货运动轨迹 图13 自动装卸货全过程 通过控制系统的整体仿真和模拟现实的工作情况,可以验证得出本自动装卸货AGV的控制算法及控制流程可以满足库前区自动装卸货的工作任务,所设计的控制算法满足精度要求。 AGV实验测试环境如图14(a)所示,在测试范围内布设适量用于定位与导航的激光反光柱,搭建模拟取放计量周装箱的车厢环境及登车桥。图14(b)为AGV实物图,采用单货叉形式,装配了距离传感器和深度视觉相机。 图14 AGV实验测试 在AGV的运行路径上设置固定的站点编号,使AGV在站点间进行直线运行和圆弧曲线运行。在AGV上安放激光灯指示器,在站点放置坐标纸以记录激光灯指示器到达指定位置所投射的坐标。依据AGV每次到达目的地后测得2个激光指示灯位置坐标的变化数据,求解雷达中心的位置坐标的变化量和姿态角度的变化量,从而得到AGV在控制算法下的重复停止精度变化,如图15、16所示。 从图15、16可以看出:AGV行驶到各个站点位置时其横、纵坐标偏差保持在±6 mm以内,姿态偏差角度保持在±0.8°以内。由此可知,AGV在实际实验环境运行时具有较高的运行控制精度,具备实验现场的应用。 图15 站点的横纵坐标偏差值 图16 站点姿态偏差角度值 电能计量检定自动化无人化是电网智能化发展的重要环节,作为计量检定中心库前作业区自动化起始区域主体的AGV,其控制算法和控制精度都影响着出入库的作业效率。为此,本文对AGV的控制系统进行建模和仿真,重点介绍在控制设计过程中的算法仿真分析及整体控制流程的运动仿真分析。根据控制系统的要求建立控制模型和仿真模型,搭建运行环境以模拟自动装卸货的全部过程,同时利用现场测试的实验数据验证该控制系统的准确性。仿真及实验结果表明本文所设计的自动装卸货AGV的控制算法及控制流程可满足计量中心库前区自动装卸的工作任务要求,仿真设计控制算法满足精度要求,可为实际AGV装置的开发调试节省大量的时间并可有效避免物理碰撞事故发生。3.2 圆弧行驶路径仿真


3.3 原地旋转仿真
3.4 装卸货时方向调整路径仿真
3.5 控制系统运行仿真
4 控制系统实验验证



5 结束语

