电压偏差及三相不平衡对电缆线路损耗的影响

陈子辉，吴智影，刘贺，陈德

(1.广东电网有限责任公司江门供电局，广东 江门 529000；2.广东工业大学 自动化学院，广东 广州 510006)

随着各类新能源、电力电子器件、非线性负荷和冲击性负荷在电力系统中的应用日益广泛，配电网中电压偏差、三相不平衡等电能质量问题日趋严重[1-4]。当电网中存在上述电能质量问题时，传统的计算方法将会产生较大的误差，难以正确评估线路损耗(以下简称“线损”)[5-6]。

目前国内外的科研人员在线损计算方面已经做出了不少成果[7-10]，但是针对电能质量影响的线损计算尚欠深入。文献[11]分析了高次谐波对电缆线损的影响，提出优化电缆参数设计以及线路敷设方式减小高次谐波的影响。文献[12]系统地分析了配电网出现三相不平衡时对线损的影响，并结合改进的等值电阻法计算了相应的线损增加率。文献[13-14]利用了遗传算法以及人工神经网络来计算线损，这种方法的准确性容易受训练数据影响，在实际生产应用中难以推广，特别是涉及到电能质量问题的影响。

鉴于目前电缆线损的研究主要围绕单一电能质量问题影响，不能准确反映不同电能质量问题共同影响下的电缆线损，本文系统论述了电压偏差、三相不平衡单独影响下配电网电缆线芯损耗的变化规律及相应的计算，从理论上推导了两者共同影响下的电缆线芯损耗计算模型，然后通过MATLAB建模进行量化分析，最后通过现场试验，验证该计算模型的准确性。

1 电能质量问题影响下的损耗计算模型

配电线路常用π型等效电路进行等效代替[15]，主要的电气参数有电阻R、电感L和对地电容C，单位长度电缆等效电路如图1所示。

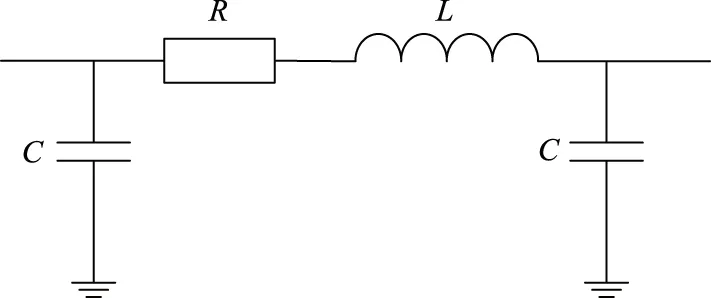
图1 单位长度电缆等效电路

在电缆线路正常运行时，单位长度电缆线路上产生的线芯损耗为

(1)

式中：S为该段线路末端所接的负载容量；U为该段线路末端的电压；R0为单位长度电缆交流电阻。

1.1 电压偏差线损模型

根据式(1)可得电压偏差下电缆的电阻损耗

(2)

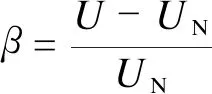
比较式(1)和式(2)可得：在线路存在较大的电压偏差时，线损如果按照式(1)采用额定电压计算时，将会产生较大的误差。故通过考虑电压偏差β，量化分析在配电网发生电压偏差电能质量问题时线损的变化。

由式(2)可以看出：对于恒阻抗负载，首端电压越高，配电网末端的负载越大，线路上的电流越大，相应的配电网上的线损也越大；相反，如果电压越低，配电网上的线损也越小。对于恒功率负载，当配电网传输功率不变时，电压越低，线路上流过的电流就越大，相应的配电网的损耗就越大。

1.2 三相不平衡线损模型

三相不平衡时电缆线芯电阻损耗计算模型的推导过程如下。

首先只考虑幅值不平衡。用εA、εB、εC分别表示A、B、C三相不平衡程度[17]，其定义为

(3)

式中：IX为X(X分别取A、B、C)相电流有效值；Iav为三相电流有效值的平均值。根据IA+IB+IC=3Iav，可得

εA+εB+εC=0.

(4)

三相幅值不平衡时，相线上的损耗

(5)

当三相不对称运行时，中性线由于不平衡电流的存在而产生附加损耗，且不平衡程度越大，产生的损耗越多。中性线上流过的不平衡相电流

I0=IA+α2IB+αIC=

Iav(1+α2+α)+Iav(εA+α2εB+αεC)=

Iav(εA+α2εB+αεC).

(6)

式中α为相量因子。

设中性线的电阻为RN，在三相幅值不平衡时，中性线上的附加损耗

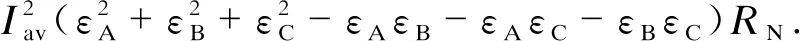
(7)

以上只是讨论了三相电流幅值不平衡时的损耗计算。在三相四线制配电网中，相角不对称对各相的电流大小没有影响，但会在中性线上产生不对称电流，进而影响中性线的损耗[17]。以A相相角φA为参考，三相电流可表示为：

(8)

中性线上流过的电流

(9)

假设:

m=1+εA+(1+εB)cosφB+(1+εC)cosφC.

(10)

n=(1+εB)sinφB+(1+εC)sinφC.

(11)

可得

(12)

由式(12)可知，当三相电流相角不对称时，即使三相电流幅值相同，在中性线上仍然有电流流过，产生电能损耗。综上所述，电缆在三相不平衡时线芯损耗

(13)

1.3 综合计算模型推导

在实际电网运行过程中，电压偏差和三相不平衡往往是同时出现的，因此必须考虑它们的共同作用对线损的交互式影响[18-21]，需要在式(2)、(13)的基础上，通过分析2种电能质量问题共存对线损的综合影响，才能得到完整的电缆线损计算式。假设配电网三相所接总负载额定容量恒定为SN，定义单相负载率

(14)

式中：Sav=SN/3，为每相负载的额定值；SX为X(X分别取A、B、C相)相实际负载。在三相平衡状态下，A、B、C相平均承担负载是Sav，此时αX=1。当三相负载不平衡且线路末端电压发生偏差时，以A相为例进行分析，则A相电流

(15)

依此类推，可以分别计算出此时B、C两相的电流。最后得到三相基波电流平均值

(16)

将式(15)、(16)代入式(3)可得此时A相电流的不平衡度

(17)

同理，可以得到此时B、C相的电流不平衡度εB、εC，将它们代入式(10)、(11)、(13)可得：

m=αA+αBcosφB+αCcosφC.

(18)

n=αBsinφB+αCsinφC.

(19)

(1+αC)2)R0+(m2+n2)RN].

(20)

式中：Pall为电缆线芯综合损耗；Iav(β)表示Iav受电压偏差度β的影响。式(20)即为考虑电压偏差、三相不平衡2种电能质量问题影响的电缆线芯损耗综合计算模型。

2 仿真计算

利用MATLAB/Simulink搭建的三相四线系统仿真模型如图2所示。

采用三相可编程电压源，选用线路模块等效电缆，根据现场试验所用的电缆型号，设置线路模块在工频下的交流电阻为R0=0.153 Ω/km，电感为L=0.634 mH/km，电容为C=0.127 μF/km，供电距离l=0.3 km，负载大小为120 kW。在电压偏差仿真中用三相负载模块，在三相不平衡及组合仿真中用3个单相负荷模块组成，每个模块的容量为40 kW。

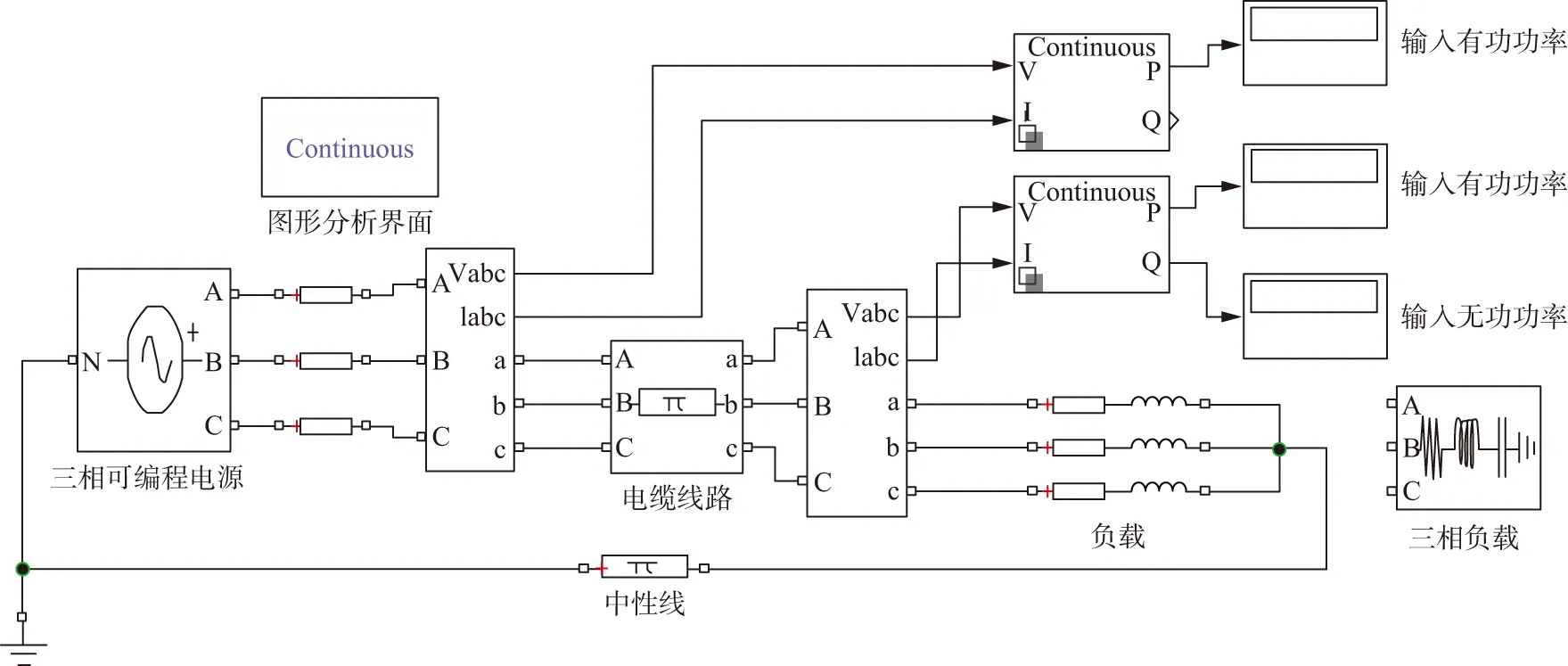
图2 仿真模型

2.1 电压偏差对电缆损耗的影响

改变电压源的电压大小，以1%的步长下降，记录每一次仿真后线路的损耗功率。为了进一步量化分析电压偏差对线损的影响，用附加损耗增率量化电能质量指标与附加线损之间的关系，可表示为

(21)

式中:ΔP为附加损耗增率；P1为电能质量问题影响下的线损值；P为理想运行状态下线损值。

根据仿真计算的线损数据，可以得到在电压偏差影响下，线路的损耗以及附加损耗增率随电压偏差变化而变化,结果见表1。由表1可知：线路首端的电压越低，线路上的电流越小，相应的线损也越小；当电压降低15%时，线路的损耗将会减小28.46%。本文所用的仿真负载类型是恒阻抗负载，实际配电网电压偏差影响的线损会随着负荷种类的不同有所变化。

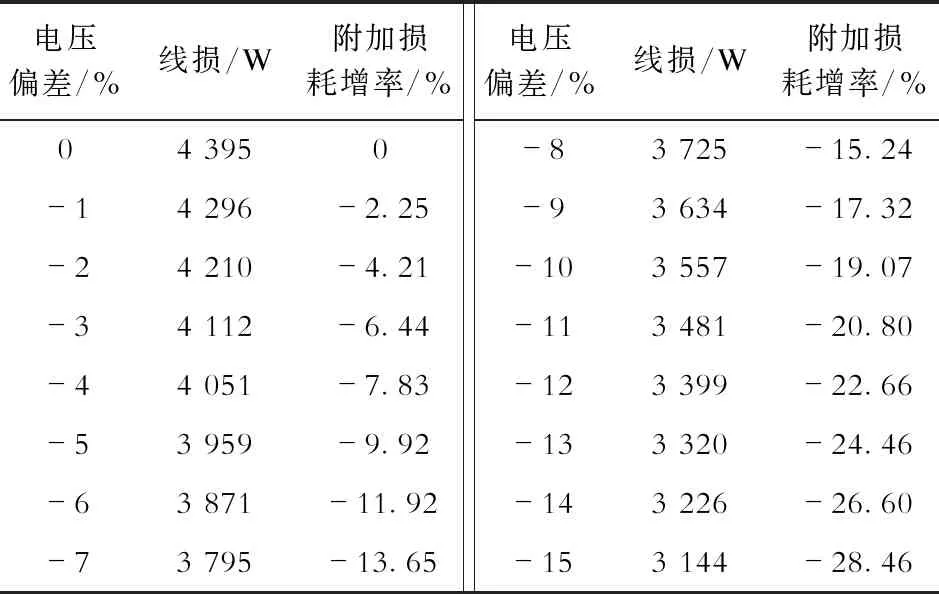
表1 电压偏差下的线损以及附加损耗增率

2.2 三相不平衡对电缆损耗的影响

改变线路上的三相不平衡度，以1%步长变化,仿真计算得到线损以及附加损耗增率随三相不平衡度变化而变化，结果见表2。由表2可知：三相负荷平衡运行状态下，中性线上没有电流，线路的损耗最小；当电网发生三相不平衡时，线损随着三相不平衡度的增加而增大；当三相不平衡度达到15%时，线路的损耗将会增加4.80%。

由第1.2节可知，三相不平衡时线损的增加主要是因为中性线电流不为零，从而在中性线上产生损耗。在中性线电阻与相线电阻大小相等时，中性线损耗在总的线损中的占比随三相不平衡度变化曲线如图3所示。

由图3可以看出：三相不平衡时，中性线上产生的附加损耗随着负载率的降低而升高，占总线损的比例逐渐增大；当不平衡度增加到15%时，中性线附加损耗占比达到11.54%。

表2 三相不平衡下的线损以及附加损耗增率

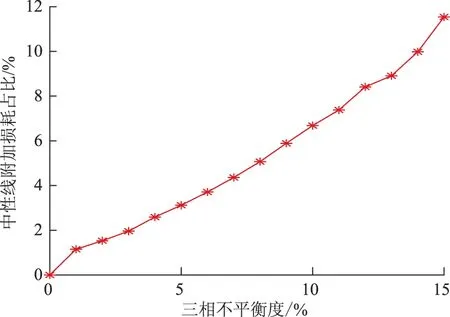
图3 中性线附加损耗的占比(%)

为了改善配电网三相不平衡问题，可以采用以下措施：

a)在地区配电网规划建设的时候，将不对称负荷分散接到不同的供电点并合理分配到各相，尽量使其平衡化，减小集中连接。

b)在配电网运行时，可以采用换相开关进行换相投切负荷，使各相上的负荷进行平均分配；还可以装设附加不平衡补偿装置，对用电负荷进行不对称补偿，把不平衡的三相负荷变换成平衡的三相有功负荷。

3 现场试验验证

进一步验证上述损耗评估模型在实际电网中的准确性，在10 kV/380 V电能质量综合试验平台上对电缆线路进行现场试验，测量计算电压偏差、三相不平衡2种电能质量问题影响下的电缆损耗。该试验平台的整体结构图如图4所示。

注：CT—电流变压器，current transformer的缩写；PT—电压互感器，potential transformer的缩写。

图4 10 kV/380 V电能质量综合试验平台整体结构示意图

Fig.4 Schematic diagram of the overall structure of the 10 kV/380 V power quality comprehensive test platform

该电能质量综合试验平台主体包括电源(连接外部10 kV电网)、扰动源、线路、负载以及各类测量记录仪器。在本次试验中，试验的设备是电缆线路，线路末端连接的是120 kW恒阻抗负载。试验采用低压电力电缆，20 ℃时导体直流电阻R0=0.153 Ω/km，允许载流量为270 A。考虑到实际电缆铺设中经常需要进行拼接，试验所用的电缆是4段拼接电缆，整个电缆线路总共有5个接头，其中首、末两端的连接如图5所示。

图5 电缆首、末端实物连接图

3.1 电压偏差试验

加入电压负偏差扰动，以1%的步长变化，记录每次试验的电缆线路首、末端的电压、电流瞬时值。分析计算得到电缆线损的仿真值与试验值随电压偏差程度变化的曲线如图6所示。

从图6可以看出，利用Simulink仿真计算得到的线损数据与现场试验测量得到的数值相差不大。对于恒阻抗负载，电压越小，线路电流越小，线损更低。

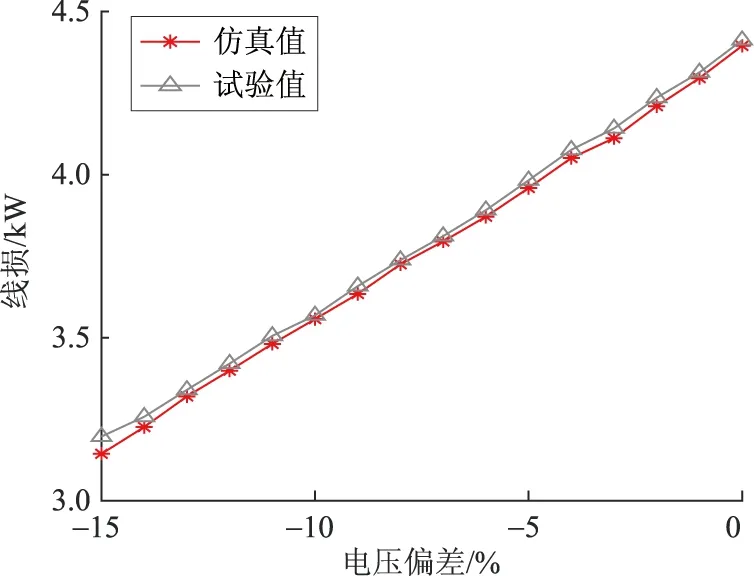
图6 线损随电压偏差变化的曲线

3.2 三相不平衡试验

按照1%的变化步长，改变线路上的三相不平衡度，得到线损的仿真值和试验值随三相不平衡度变化而变化的曲线如图7所示。

图7 三相不平衡时的线损

由图7可知，仿真计算得到的电缆线损与试验测量得到的线损基本相符，且试验值略大于仿真值。由于仿真所用的线路模型与现场试验的电缆线路相比仍然存在一些差异，仿真值与现场试验的值始终存在误差，但误差变化不大，基本稳定在1.1%内，满足工程计算要求。

3.3 综合试验

当电压偏差、三相不平衡同时发生时，由于两者的交互作用，要利用线损综合式(20)计算模型才能准确计算此时的线路电阻损耗。在仿真模型和试验平台里同时设置不同的电压偏差和三相不平衡度，测量相应的线路电阻损耗，通过对比仿真计算的理论值以及现场试验的测量值，验证该计算模型的准确性，试验过程如下：

负载端考虑不同的负载率分别设置为60 kW、120 kW、180 kW恒阻抗负载。对于120 kW负载，电压偏差设置为-1%到-10%，以-1%为步长；三相不平衡度设置为1%到10%，以1%为步长。对于负载60 kW、180 kW，电压偏差分别设置为-5%、-10%；三相不平衡度分别设置为5%、10%。

根据120 kW负载综合试验测量得到的线损数据，与式(20)综合模型对应的仿真计算值进行对比，可以得到不同电压偏差以及三相不平衡度下的试验值的百分比误差，如图8所示。

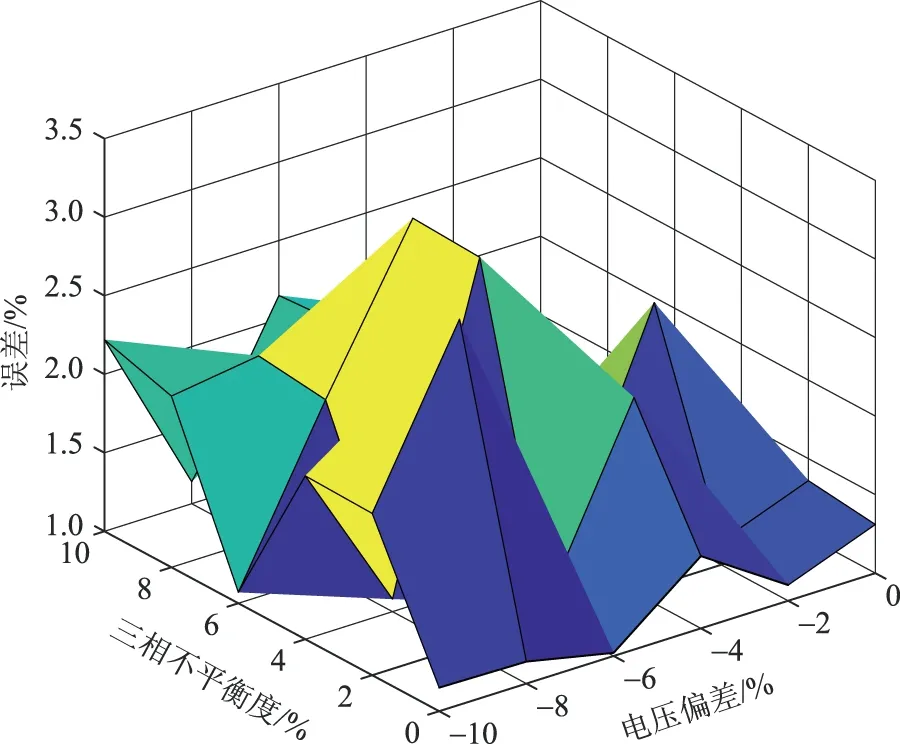
图8 试验值的百分比误差

由图8可以看出，通过现场试验测量得到的线损与仿真计算值的误差在3.5%的范围内，从而验证了存在2种电能质量因素时，可以利用该综合计算模型对线路的电阻损耗进行计算评估。

部分仿真计算得到的线损理论值和综合试验得到的线损测量值见表3。

由表3可以看出，在不同的负载情况下，采用式(20)综合计算模型，即计及电压偏差和三相不平衡综合影响时，低压电缆线损的仿真计算值与在试验平台中得到的线损试验测量值基本相符。

表3 综合仿真结果对比

4 结束语

本文研究了电压偏差、三相不平衡对电缆电阻损耗的影响，并结合仿真模型和现场试验，对不同电能质量因素单独影响时的线损进行量化分析。在上述2种电能质量因素对电缆损耗的单独影响机理基础上，通过分析电压偏差和三相不平衡的交互影响，推导出它们共同作用下的电缆线路电阻损耗综合计算模型。最后利用电能质量综合试验平台，对电缆线路进行电压偏差、三相不平衡2种电能质量问题的现场试验，现场测量得到的线损数据结果验证了本文提出的综合计算模型可以准确评估电压偏差、三相不平衡共同影响时的线损值。