正交各向异性功能梯度微板弯曲行为尺度效应

康泽天，张岩，周博，薛世峰

（中国石油大学(华东)储运与建筑工程学院，山东青岛，266580)

功能梯度材料是材料组分或几何尺寸沿结构特定方向成连续梯度变化的一种新型材料，具有消除应力集中、减小残余应力、增强连接强度和减小裂纹驱动力等许多普通均质材料不具备的优异性能，广泛应用于航空航天、人工智能和微机电系统等领域[1-3]。随着微电子科技发展，功能梯度微纳结构的应用愈发广泛，其在不同加载条件下的力学行为研究得到青睐。众多微观实验发现并证实，当结构几何尺寸进入到微/纳米量级时，其材料力学行为具有明显的尺度效应[4-5]。为合理解释尺度效应，许多专家学者在材料本构关系中引入与微观结构相关的特征尺度参数，相继提出应变梯度理论和偶应力理论等非经典弹塑性理论，描述材料力学行为的尺度依赖性。偶应力理论因引入较少的特征尺度参数，更适合工程实际建模。YANG 等[6]在偶应力理论基础上，提出修正偶应力理论，只引入1个长度尺度参数，在不失准确性的前提下，简化建模过程，在微纳结构领域应用最为广泛；PARK 等[7]基于该理论建立了能够描述Bernoulli-Euler 梁弯曲行为尺度效应的力学模型，通过与试验结果进行对比，验证模型的准确性；ASGHARI等[8-9]基于修正偶应力理论，在线弹性范围建立了能够描述功能梯度Euler-Bernoulli 和Timoshenko 微梁弯曲及自由振动尺度效应的力学模型；KE 等[10]基于修正偶应力理论分析功能梯度Timoshenko 微梁的动态稳定性问题；在修正偶应力理论的基础上，REDDY[9]和NATEGHI 等[11]分析多种功能梯度微梁的屈曲，并探讨边界条件对屈曲临界载荷的影响。除此之外，许多专家学者对微板力学行为的尺度效应进行了理论研究。TSIATAS[12]基于修正偶应力理论和Kirchhoff 板理论，建立能够描述不同边界条件下任意边界形状微板弯曲行为尺度效应的力学模型；KE 等[13]基于修正偶应力理论和一阶剪切变形板理论，研究不同边界条件下Mindlin 微板自由振动行为，并分析材料尺度参数和板跨厚比等因素对尺度效应的影响；THAI 等[14]基于Kirchhoff, Mindlin 和Reddy 板理论对功能梯度微板弯曲、自由振动和屈曲行为进行理论建模，并探讨材料尺度参数对板弯曲挠度、自振频率以及屈曲载荷的影响；LOU 等[15]考虑几何非线性，基于修正偶应力理论提出1种能够描述功能梯度微板尺度效应的统一高阶板理论，并利用哈密顿原理推导微板的控制方程和边界条件。上述研究对象均为各向同性材料结构，随着材料科学的发展和研究逐渐深入，许多专家学者对各向异性功能梯度微结构的力学行为进行理论建模分析。GUO等[16-17]基于修正偶应力理论，研究各向异性复合板的弯曲行为，并分析功能梯度参数和材料长度对微板位移场和应力场尺度效应的影响；CHEN 等[18]在修正偶应力理论基础上提出1种适用于各向异性材料的新修正偶应力理论，并开展一系列有关层合梁板结构弯曲、振动和稳定性等问题的研究[19-20]；贺丹等[21-22]基于新修正偶应力理论，研究平面正交各向异性功能梯度微梁以及斜交铺设层合Kirchhoff 微板弯曲行为的尺度效应；YANG等[23]基于新修正偶应力理论和虚功原理研究正交各向异性功能梯度Kirchhoff 微板弯曲变形过程中挠度和正应力的尺度效应。上述研究均假设材料参数以幂指数形式变化，定性分析各向异性和指数变化对微结构挠度、应力和固有频率尺度效应的影响，但没有定量分析微结构考虑尺度效应的几何尺寸参数以及对微结构中偶应力尺度效应。本文作者基于新修正偶应力理论和Kirchhoff 板理论，研究材料参数沿板厚方向呈正弦梯度变化的正交各向异性简支微板的静弯曲行为，重点考察各向异性和功能梯度参数对微板挠度、正应力和偶应力尺度效应的影响，为微电子机械系统(MEMS)中微结构的理论分析和优化设计提供理论基础和技术参考。

1 新修正偶应力理论

CHEN 等[18-20]提出新修正偶应力理论，并给出弹性体应变分量εij和曲率分量χij的表达式为：

式中：ui为平动位移分量；

式中：ωi为转动位移分量；eijk为置换符号；uk,j为位移分量uk对j坐标的偏导数；下标j和k均为哑标；下标i为自由标。

各向异性弹性体的本构关系可以描述为：

式中：σij为应力分量；Dijkl为弹性常数分量；mij为偶应力分量；Gi和Gj分别为2个正交方向的剪切模量；li和lj分别为2个正交方向的材料尺度参数。

2 正交各向异性功能梯度微板模型

2.1 基本变量描述

图1所示为任意横向分布载荷作用下Kirchhoff微板示意图，其中，xy平面与微板中面重合。

根据Kirchhoff 板假设，板的位移场可以表示为

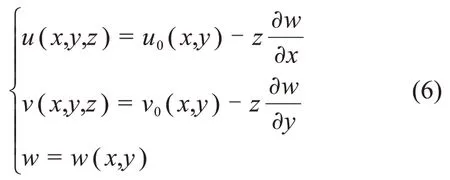
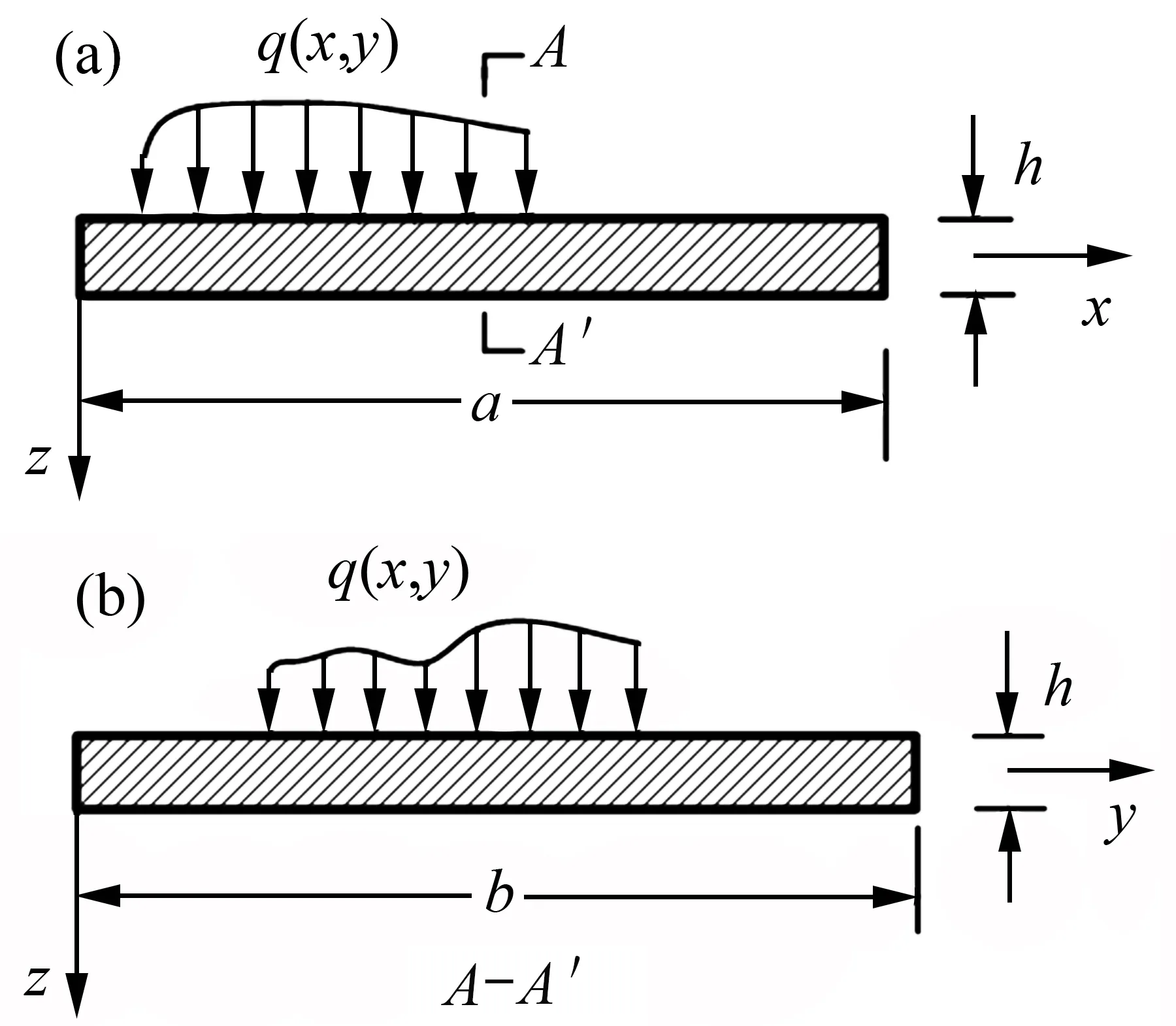
图1 横向载荷作用下正交各向异性微板示意图Fig.1 Schematic diagram of orthotropic microplate under transverse load

式中：u，v和w分别为板内任意一点沿x，y和z方向上的位移分量；u0和v0分别为变形后，板中面沿x和y方向上的位移。将式(6)代入式(1)，得到微板的非零应变分量为

将式(6)和式(3)代入式(2)，得到微板的非零曲率分量为

由式(4)可知本构关系可以表示为：

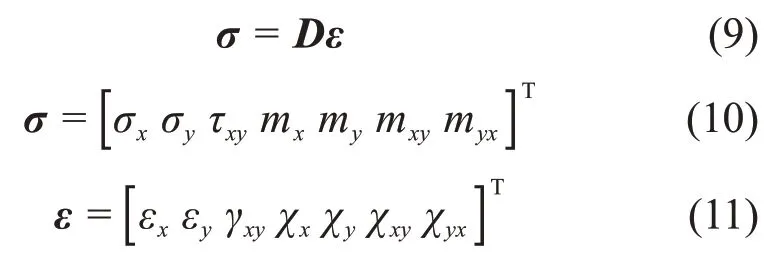
式中：D为刚度矩阵；σ和ε分别为应力列向量和应变列向量。刚度矩阵D中非零元素为

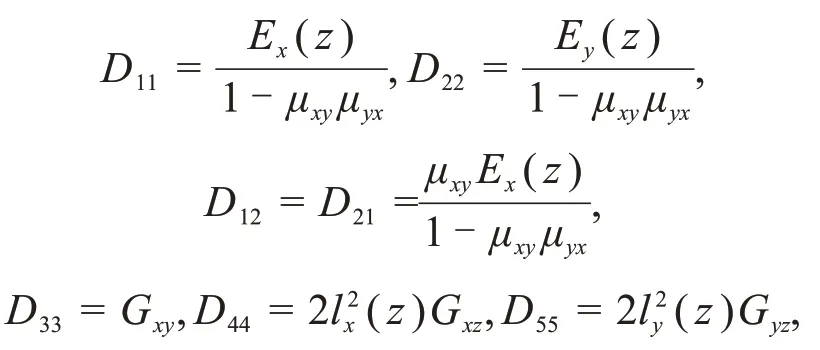
式中：μxy和μyx为材料不同方向的泊松比；Ex和Ey分别为材料沿x和y方向的弹性模量；Gxy，Gxz和Gyz分别为材料xy，xz和yz方向的剪切模量；lx和ly分别为材料沿x和y方向的特征尺度参数。

2.2 基于最小势能原理的平衡方程

最小势能原理表述为在一个保守系统的所有可能位移场中，真实位移场引起系统的总势能取最小值，即总势能的一阶变分为零，表示为

式中：П为总势能；U为弹性应变能；Vp为外力势能。弹性应变能变分运算结果为

将式(7)和式(8)代入式(13)，得

式中：

微板在横向分布载荷q(x,y)作用下的外力势能变分为

将式(14)和(15)代入式(12)，得

将式(7)和式(9)代入式(16)，得

式中：

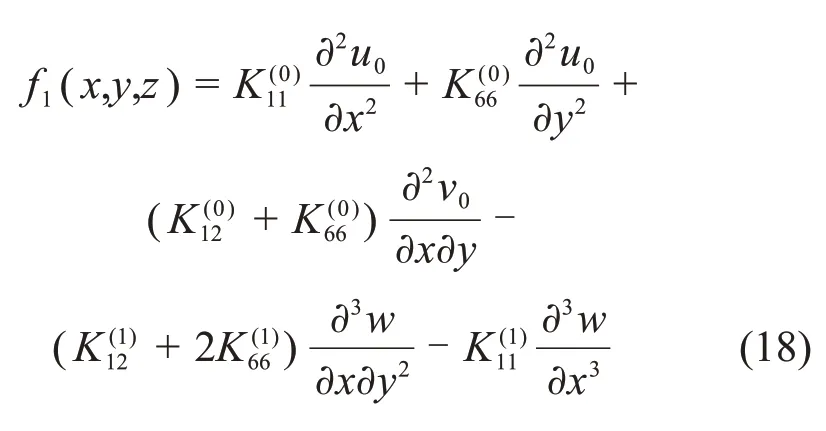
式中：

对任意δu0，δv0和δw，式(17)均成立，可得

式(21)即为微板静力学平衡方程。当lx= 0，ly=0时，式(21)将退化为经典弹性平衡方程。

3 尺度效应

工程中任何形式的载荷均可描述为三角级数的形式，为突出微板结构所承受实际载荷的复杂情况和本文解的普遍性，本节以受双向正弦载荷的四边简支微板为例，如图2所示，研究正交各向异性功能梯度微板弯曲行为的尺度效应。其中，a，b和h分别为微板的长度、宽度和厚度。其材料参数Ex，Ey，Gxy，Gxz，Gyz，lx和ly均沿板厚方向呈正弦梯度变化，如图3所示，梯度函数为

式中：X为微板材料参数，上标s 表示微板表面；上标c表示微板中面；

α为定义的量纲一功能梯度参数，当α=1时，材料模型退化为正交各向异性均质模型。

图2 双向正弦载荷作用下正交各向异性功能梯度简支微板示意图Fig.2 Schematic diagram of orthotropic functionally graded simply supported microplate under bidirectional sinusoidal load

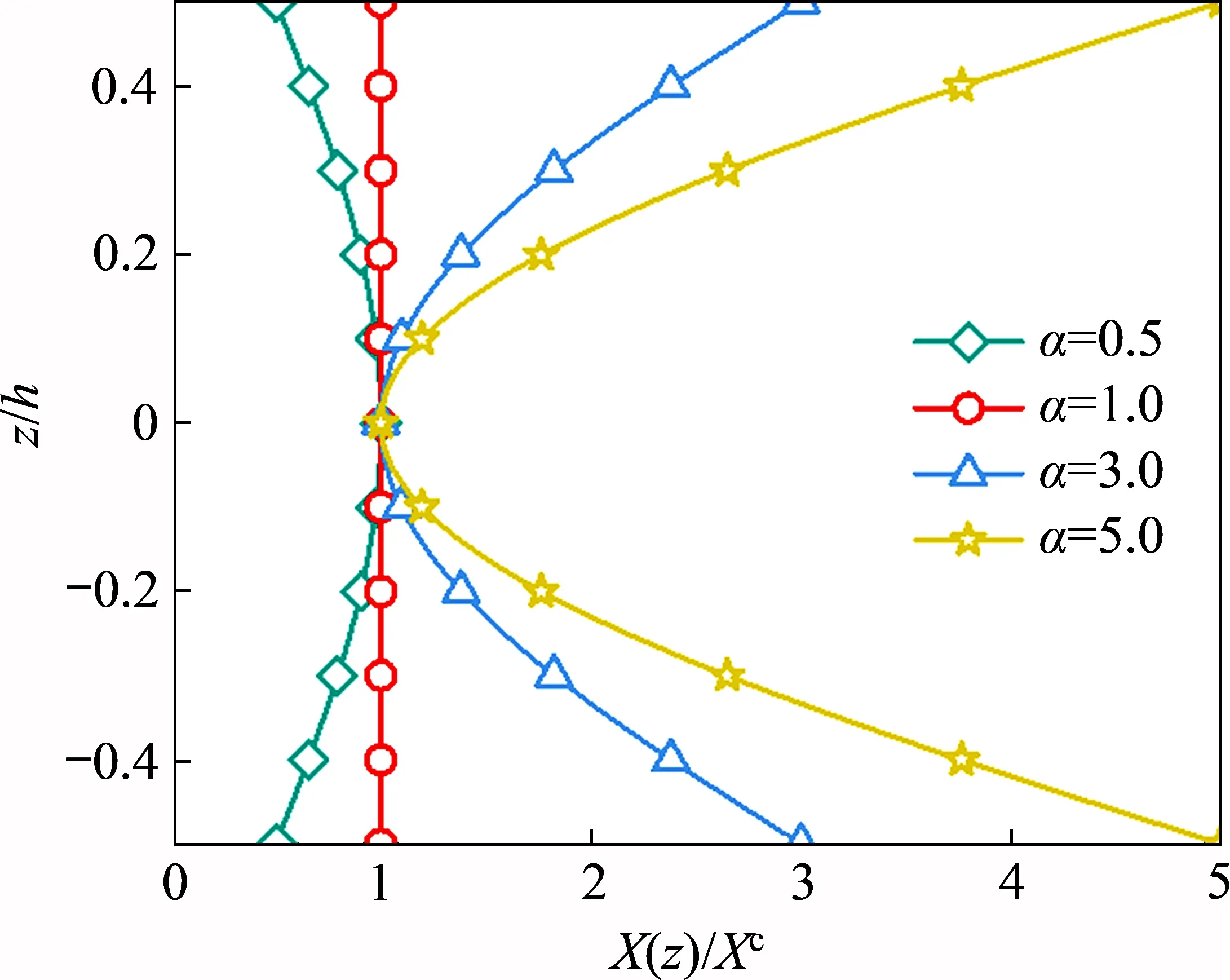
图3 功能梯度简支微板截面材料参数梯度变化示意图Fig.3 Schematic diagram of material parameter graded variation in the functionally graded simply supported microplate section

作用于微板的载荷函数关系式为

式中：q为微板所受横向分布载荷；q0为常数。

简支微板的位移边界条件

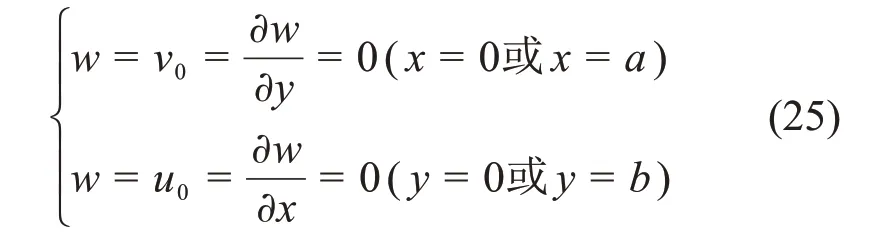
设满足式(25)的位移势函数为

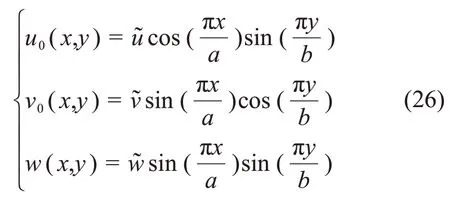
式中：和为待定系数。将式(26)和(18)～(20)代入式(21)，得

式中：

将式(26)代入式(7)和式(9)，可得微板正应力和偶应力表达式为

为了便于分析，定义量纲一坐标x'和y'，量纲一挠度w'，量纲一正应力σx'和σy'以及量纲一偶应力mx'，my'和mxy'的表达式分别为

式中：和分别为不考虑尺度效应即材料特征尺度参数lx=0和ly=0时的经典正应力。

根据上述力学模型，对正交各向异性功能梯度简支微板在双向正弦载荷作用下的挠度，正应力和偶应力分布进行数值计算。其中，载荷参数q0=1 000 MPa，微板的结构尺寸为a=b=0.2 mm,h=0.025 mm,其材料参数如表1所示。

表1 正交各向异性功能梯度微板材料参数[23]Table 1 Material parameters of orthotropic functionally gradient microplate[23]

4 讨论

4.1 挠度分析

图4 所示为量纲一功能梯度参数α=1 时，微板量纲一挠度变化曲线。图4(a)可见：微板沿x方向的挠曲线均呈正弦分布，且最大挠度出现在微板中间位置。由图4(b)可见：当h/lx较小时，微板量纲一挠度较小，当h/lx小于5 时，微板挠度具有明显的尺度效应。随着h/lx增大，量纲一挠度逐渐增大，但增大程度逐渐减缓，表明h/lx对微板沿x方向挠曲线的影响逐渐减弱，当h/lx大于10时，随着h/lx增大，微板最大量纲一挠度基本保持恒定，微板挠度的尺度效应消失。除此之外，随着h/ly增大，微板最大量纲一挠度逐渐增大，但增大程度逐渐减缓，表明h/ly也是影响微板挠度尺度效应的重要因素。

图4 量纲一挠度曲线特征Fig.4 Dimensionless deflection curves

图5所示为不同功能梯度参数情况下微板中心最大量纲一挠度的变化曲线。由图5可见：当功能梯度参数较小时，微板最大量纲一挠度较小，随着功能梯度参数增大，微板最大量纲一挠度逐渐增大，但增大程度逐渐减缓，表明功能梯度参数对微板挠度的影响逐渐减弱。对比图5(a)和5(b)可以发现：材料沿2个正交方向的长度尺度参数对微板挠度尺度效应的影响程度不同。

4.2 正应力分析

图6 所示为量纲一功能梯度参数α=1 时，微板量纲一正应力σx'在x=a/2处截面沿y方向的变化曲线。由图6可见：微板量纲一正应力σx'均沿y方向均呈正弦分布，且最大正应力出现在微板中间位置。当板厚与材料长度尺度参数比值较小时，微板量纲一正应力较小，微板正应力具有明显的尺度效应。随着板厚与材料长度尺度参数比增大，量纲一正应力逐渐增大，但增大程度逐渐减缓，表明板厚与材料尺度参数比对微板正应力沿y方向变化曲线的影响逐渐减弱，微板正应力的尺度效应逐渐消失。对比图6(a)和6(b)可以发现：材料沿2个正交方向的材料尺度参数对微板正应力的尺度效应影响程度不同。

图7 所示为微板最大量纲一正应力σx'随板厚与材料x方向长度尺度参数比值的变化曲线。由图7(a)可见：当h/lx小于5时，微板正应力具有明显的尺度效应。当h/lx大于10时，微板最大量纲一正应力基本保持恒定，微板正应力的尺度效应消失。除此之外，随着h/lx和h/ly同时增大，微板最大量纲一正应力逐渐趋近于1，即微板最大正应力的新修正偶应力理论解逐渐趋近于不考虑尺度效应时的经典弹性理论解，从而验证了本文结果的准确性。由图7(b)可见：当功能梯度参数较小时，微板最大量纲一正应力较小，随着功能梯度参数增大，微板最大量纲一正应力逐渐增大，但增大程度逐渐减缓，表明功能梯度参数对微板正应力的影响逐渐减弱。

4.3 偶应力分析

图7 微板最大量纲一正应力随h/lx的变化曲线Fig.7 Maximum dimensionless normal stress of microplate vs.dimensionless thickness h/lx

图8(a)所示为h/lx取值不同时，微板量纲一偶应力mx'在x=a/2处截面沿y方向的变化曲线。由图8(a)可见：微板量纲一偶应力mx'均沿y方向呈余弦分布，且最大偶应力出现在微板边界位置，中心处偶应力为零；当h/lx较小时，微板量纲一偶应力较大。随着h/lx增大，量纲一偶应力逐渐减小，但减小程度逐渐减缓，表明h/lx对微板偶应力的影响逐渐减弱，尺度效应逐渐消失。图8(b)所示为h/ly取值不同时，微板量纲一偶应力mx'在x=a/2 处截面沿y方向的变化曲线。由图8(b)可见：当h/ly较小时，微板量纲一偶应力较小；随着h/ly增大，量纲一偶应力逐渐增大并趋于稳定值，表明h/ly对微板偶应力的影响逐渐减弱，尺度效应逐渐消失。

对比图8(a)和8(b)可以发现：沿2 个正交方向的长度尺度参数对微板偶应力的尺度效应影响程度不同。材料x方向长度尺度参数对微板量纲一偶应力mx'的影响较大，材料y方向长度尺度参数对微板量纲一偶应力mx'的影响较小。h/lx减小对量纲一偶应力mx'具有减弱作用，而h/ly减小对量纲一偶应力mx'具有增强作用。

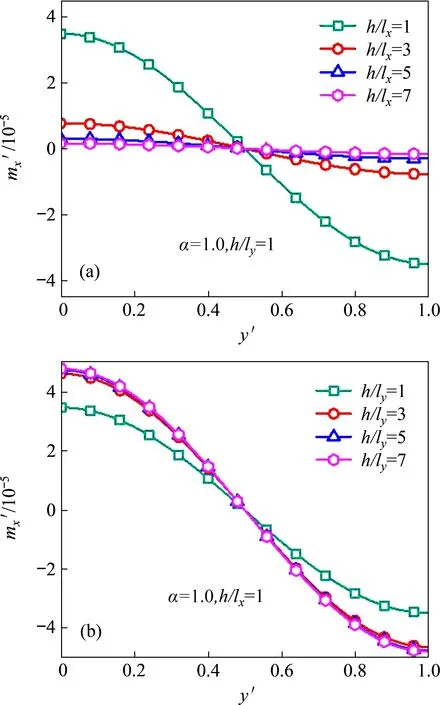
图8 微板量纲一偶应力沿y方向分布曲线Fig.8 Dimensionless couple stress curves along y direction

图9(a)所示为h/ly不同时，微板最大量纲一偶应力mx'随h/lx取值变化曲线。由图9(a)可见：当h/lx小于5时，微板最大量纲一偶应力mx'随板厚与材料尺度参数比值变化明显；当h/lx取值大于12 时，微板偶应力趋于0，尺度效应消失。图9(b)所示为不同功能梯度参数情况下，微板最大量纲一偶应力mx'随h/lx取值的变化曲线。由图9(b)可见：当功能梯度参数较小时，微板最大量纲一偶应力mx'较大；随着功能梯度参数增大，微板偶应力逐渐减小，但减小程度逐渐减缓，表明功能梯度参数对微板偶应力的影响逐渐减弱。

图9 微板最大量纲一偶应力随h/lx的变化曲线Fig.9 Maximum dimensionless couple stress of microplate vs.dimensionless thickness h/lx

5 结论

1) 基于新修正偶应力理论和最小势能原理，建立材料参数沿板厚方向呈正弦梯度变化的平面正交各向异性功能梯度微板的弯曲模型。

2)板厚与材料长度尺度参数比值越小，微板挠度、正应力和偶应力的尺度效应越明显；当板厚与材料长度尺度参数比值大于10 时，微板弯曲行为的尺度效应可以忽略不计。

3)材料沿2个正交方向的长度尺度参数对微板挠度、正应力和偶应力的尺度效应影响程度不同，且材料沿2个正交方向的长度尺度参数变化引起偶应力的变化趋势相反。

4)功能梯度参数对微板挠度、正应力和偶应力的尺度效应有一定影响，且随着功能梯度参数增大，功能梯度参数对微板挠度、正应力和偶应力的影响逐渐减弱。