粗粒土路堤填料力学特性及其细观模拟研究

何忠明，黄超，刘雅欣，范电华，杨煜

(1. 长沙理工大学交通运输工程学院，湖南长沙，410114；2. 长沙理工大学道路灾变防治及交通安全教育部工程研究中心，湖南长沙，410114)

粗粒土(颗粒粒径d在[0.075, 60.000] mm 范围内的质量占颗粒总质量的50%以上[1])是岩石体受外界环境影响未完全风化的堆积物，因其在压实情况下具有压实度高、抗剪强度大等特点，被广泛应用于高速公路路堤填筑中。但粗粒土填料初期抗压性能较差，在外力作用下较易发生压缩变形等，且雨水入渗增大了粗粒土路堤的含水率，在一定程度上弱化了路堤土体的抗剪强度，使得粗粒土路堤边坡失稳现象时有发生。长期以来，为了了解粗粒土的力学性质，人们主要应用三轴试验对粗粒土应力、应变特性进行了研究，如：SWEEREG 等[2]在三轴试验中，发现粗粒土试件轴向应变增长与轴向应力呈反比；武明[3]利用大型三轴仪器，控制粗粒土的干密度、含水率等参数对粗粒土力学特性进行了研究；秦红玉等[4]通过大型三轴试验，对高低围压下粗粒土应力应变、抗剪强度及内摩擦角进行了对比分析；胡焕校等[5]通过大型动静三轴仪器对粗粒土填料开展试验研究，分析了不同荷载频率、压实度及含水率对粗粒土填料动力特征与损伤演化的影响。上述研究者均利用试验对粗粒土的力学性能进行宏观分析，但由于受试验条件、环境等因素影响，给实验结果带来了许多不确定性[6]，试验结果往往具有较大离散性。近年来，一些研究者运用离散元程序分析粗粒土填料性质，如蒋中明等[7]基于粗粒土渗透变形试验结果，运用PFC3D软件对粗粒土的渗透性演化进行了细观分析，得出渗流过程中颗粒的移动情况；ERGENZINGER等[8]通过内置Fish语言建立了颗粒间胶结模型，并提出了颗粒间渐变破坏的离散元模型，模拟粗粒土的三轴压缩试验；陈建峰等[9]将内置的Fish 语言建立的胶结模型与摩尔-库仑准则相结合，探讨了黏性土在三轴压缩过程中宏观力学强度变化，并对颗粒之间细观参数进行了对比分析；蒋明镜等[10]以粗粒土为研究对象，通过对粗粒土建立胶结模型，分析了胶结强度和围压等因素下粗粒土的细观特性变化。综上所述，众多学者对粗粒土填料的宏细观力学特性进行了研究，但针对粗粒土填料在荷载和降雨共同作用下的细观性能演变规律还未形成共识，尤其是粗粒土填料的细观结构极为复杂，传统的连续介质力学模型无法对粗粒土的细观力学特性进行合理解释。为此，本文作者借助三轴试验与数值仿真模拟对粗粒土试验的力学性能进行研究，以粗粒土路基填料为研究对象，采用PFC3D颗粒流软件，对静三轴试验进行数值模拟，对比不同围压、压实度及含水率条件下室内试验与数值仿真的应力-应变曲线，验证模型的有效性；最后分析三轴试验过程中黏结破坏数量的发展，揭示粗粒土细观力学特性的内在作用机理。

1 试验

1.1 试验设备

试验在长沙理工大学公路养护技术国家工程实验室进行，试验仪器为Autotriax 全自动三轴试验系统，型号为Dynatriax100/14。该设备静止竖向位移可达到100 mm，最大侧压力为4 MPa，可自动采集轴向应力-应变及体应变等相关试验数据，并且能够自动加卸载。该设备主要由计算机、控制系统、气压自动调节设备、三轴室、作动器5部分组成，如图1所示。

1.2 试验土样选取

试验材料粗粒土选自湖南省某高速第一合同段，该合同段边坡土体整体为棕红色，主要成分为红壤土和矿物材料，其中红壤土呈酸性红色，可塑性较强，其体积占粗粒土总体积的82%；矿物材料主要由碎石构成，外表多棱角，孔隙率较大，抗压强度较高，其中含有部分红黏土，导致其黏聚力较大。

图1 Autotriax全自动三轴试验系统Fig.1 Autotriax fully automatic triaxial test system

首先开展常规的三轴试验，以便了解粗粒土的宏观力学特性。在三轴试验中，粗粒土试件为圆柱体，直径为100 mm，高度为200 mm，根据JTG E40—2007“公路土工试验规程”，试样粒径不能超过试件直径的1/5。本文采用最大粒径剔除法制作粗粒土试件，剔除粒径大于20 mm 的粗粒土颗粒，以便于基础试验和三轴试验的开展[11]。试验土样级配曲线如图2所示。

图2 试验土样级配曲线Fig.2 Test sample grading curve

1.3 试验方案的确定

基于以往学者的研究方案，分别考虑不同含水率(6.8%，8.7%，9.5%)、不同压实度(91%，94%，96%)和不同围压(0.3，0.6，0.9 MPa)开展试验研究[12-13]。然后，根据不同围压试验结果确定黏聚力和内摩擦角，为PFC3D离散元数值模拟提供相关的细观参数。试验方案如表1所示。

表1 不同参数条件下静三轴试验加载方案Table 1 Triaxial test loading scheme under different parameters

2 试验结果分析

2.1 应力-应变曲线分析

图3 所示为三轴试验中不同围压时的应力-应变关系[14]。由3可以看出：在相同压实度、含水率条件下，围压越大，同一轴向应变所需偏应力也就越大，其中围压为0.3 MPa的粗粒土试件，当偏应力仅为1.98 MPa时，试件的轴向应变已达12%，而围压为0.6 MPa 和0.9 MPa 时的试件则需更大的偏应力才能达到相同的应变率；在剪切应变初期，试件处于弹性阶段，随着偏应力增加，试件过渡到塑性阶段，表现为应变硬化；在高围压条件下，这种应变硬化现象较早出现。其原因是：在剪切变形过程中，当试件压实度和含水率相同时，围压越大，对试件的侧向变形约束力也就越大，从而在一定程度上导致试件产生相同轴向应变时所需要的轴向应力越大[15]。

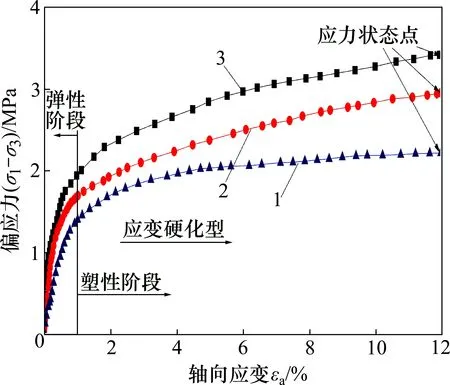
图3 不同围压时粗粒土试件应力-应变曲线Fig.3 Stress-strain curves of coarse-grained soil specimens under different confining pressures

2.2 粗粒土强度参数标定

基于强度理论与极限平衡条件，根据图3可以得到不同围压下的最大偏应力。以12%轴向应变对应的轴向应力和围压之和的一半为圆心，其坐标为以抗剪强度的一半为半径即绘制3 组不同围压下的极限应力圆，得出该试件的抗剪强度包络线，从而得到抗剪强度。

图4所示为粗粒土试件极限应力圆与抗剪强度包络线，绘制的包络线在纵坐标上的截距为黏聚力c，包络线的斜率f为粗粒土填料内摩擦角φ的正切。首先结合抗剪强度表达式τf=c+σtanφ及绘制的包 络 线 可 知：c=0.317 MPa，tanφ=0.712，φ=35.45°。

图4 粗粒土试件极限应力圆与抗剪强度包络线Fig.4 Ultimate stress circle and shear strength envelope of coarse-grained soil samples

此外，也可结合最小二乘法拟合破坏应力点的p-q法进行计算，相关的公式为：

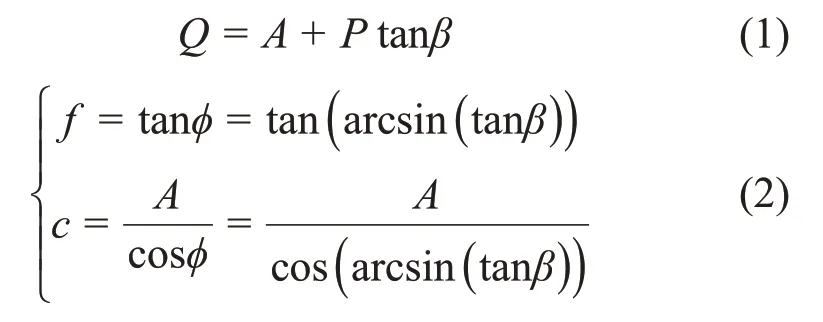
结合式(2)和主应力之间的关系式，通过计算得出c=0.274 MPa，φ=36.41°。为了准确求出粗粒土试件的抗剪强度参数，取以上2种方法的平均值作为含水率为6.8%的粗粒土试件的黏聚力及内摩擦角：c=0.296 MPa，φ=36.32°。考虑到含水率对粗粒土抗剪强度的影响，采用以上相同的研究方法，得到含水率为8.7%和9.5%时粗粒土试件对应的黏聚力c分别为0.289 MPa和0.263 MPa，内摩擦角为φ分别为35.21°和33.94°，将最终修正后的强度参数作为数值模拟的力学参数。

2.3 轴向应变与体应变曲线关系分析

体应变εv为试件初始值与剪切过程中体积差之比。图5 所示为不同围压下轴向应变εa与体应变εv的关系曲线。由图5可知：随着围压增大，试件由剪胀转为剪缩，其中围压为0.3 MPa的试件随着剪切进行表现出先剪缩后剪胀，而围压为0.6 MPa与0.9 MPa的试件在剪切过程中表现为整体剪缩。其主要原因为：围压为0.3 MPa的试件由于围压作用较小，在剪切力作用下易发生翻转和滚动，所以，宏观表现为先剪缩后剪胀；在较高围压条件下，试件在剪切过程中以颗粒间的挤密压缩为主，试件的横向膨胀为辅，颗粒间压缩挤密引起的密度增加量远大于横向试件横向膨胀变形引起的密度减小量，所以，整体上表现为剪缩；随着围压增大，试件土体的初始弹性模量逐渐增大[16-17]。

图5 不同围压条件下轴向应变εa与体应变εv的关系Fig.5 Relationship between axial strain and body strain under different confining pressures

3 数值模拟试验

3.1 生成试件模型的过程

采用Gene 生成法，通过控制制作球形颗粒的粒度、孔隙率和试件尺寸(高度和宽度)等参数生成三轴试件，生成的模型试件如图6所示。图7所示为颗粒间接触力链模型，其中模型尺寸与室内三轴试验中试件尺寸相同。

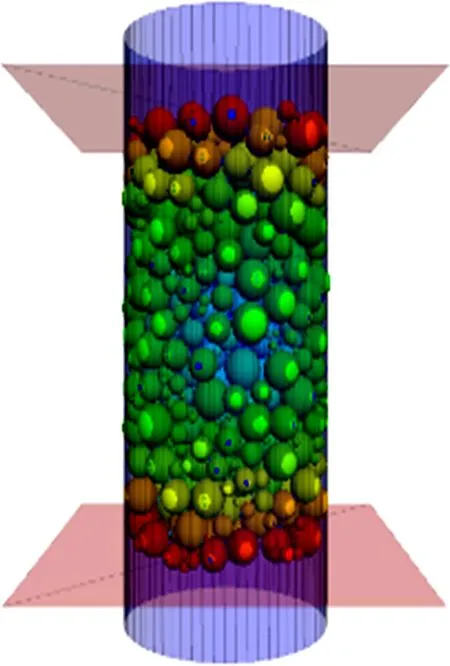
图6 三轴试件数值模型Fig.6 Numerical model of triaxial specimen

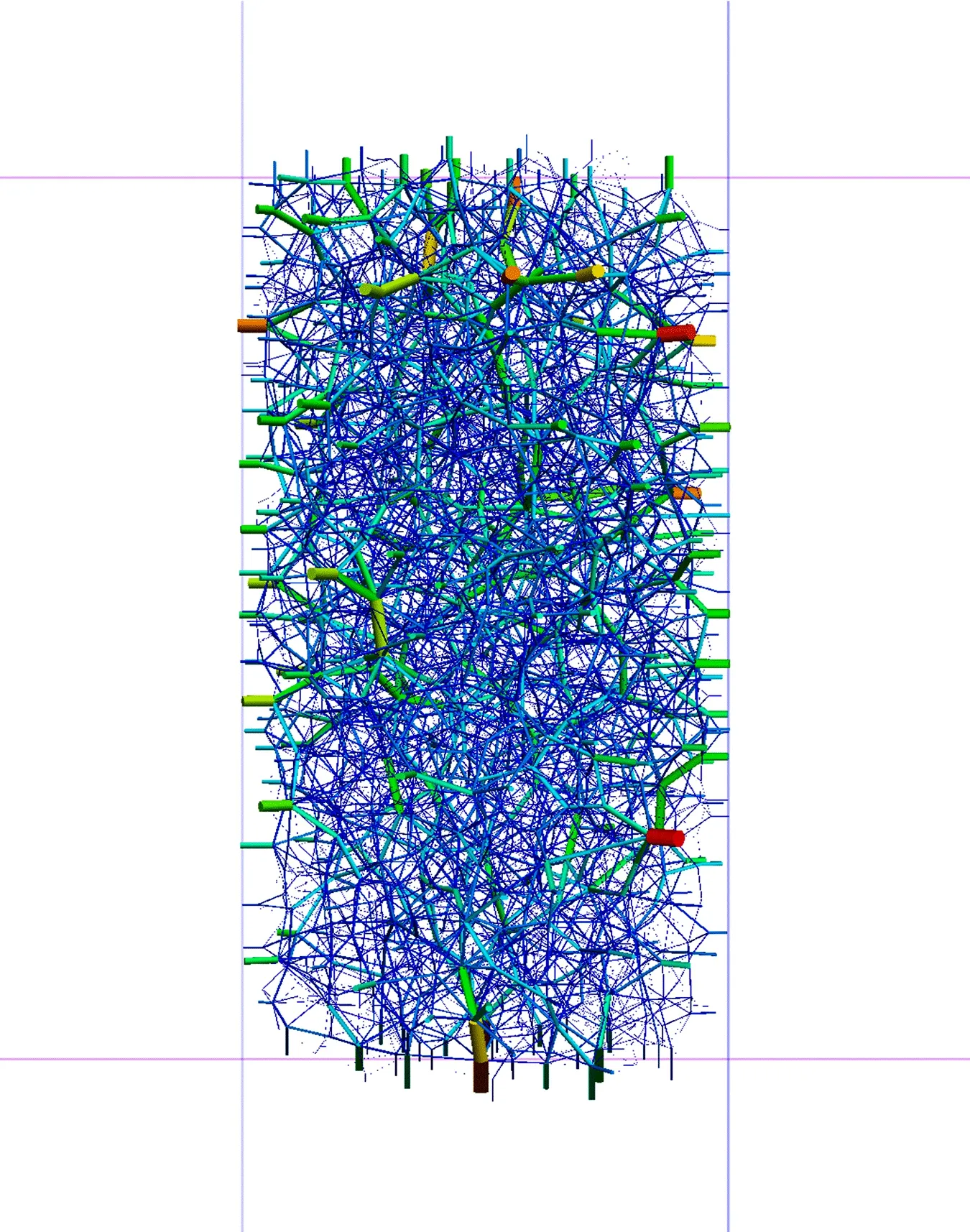
图7 颗粒间接触力链模型Fig.7 Numerical model of contact force

样本颗粒在生成过程中，若按照试样级配生成，则会在DEM生成器中生成数百万个颗粒，严重影响模型计算速率，且计算机内存无法实现计算，为此，本文借助加权平均数法得出加权平均颗粒半径R：

式中：Ri为颗粒平均半径；Mi为颗粒质量分数；Wi为颗粒加权平均数。

在利用DEM 生成颗粒流时，若仅采用最大半径与最小半径的比值，则生成不同粒径的概率相同。依据加权平均颗粒半径R，固定最小半径计算最大半径，即

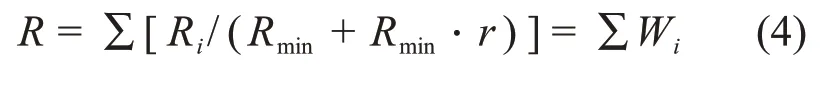
式中：r=Rmax/Rmin；Rmax为最大颗粒半径；Rmin为最小颗粒半径。根据试算得Wi，即可算出颗粒最大、最小半径比r。根据式(4)，本文采用颗粒最小半径Rmin为0.25 mm 及颗粒最大、最小半径比r为79.16进行颗粒生成[18]。

3.2 细观参数确定

以三轴试验为基础，对模拟中细观参数进行标定。由于颗粒流模型无法直接定义试件的含水率，因此，利用细观参数中的变量来模拟含水率的变化[19]。许自立[20]以屈服强度为中间变量，得出颗粒间黏结强度与含水率之间有着密切关系。本文基于以上研究，通过Fish 语言编程建立不同压实度和含水率的模型。由于抗剪强度参数会随土体含水率的变化而变化，为简化问题，采用同一含水率的试件抗剪强度参数不变，即黏聚力和内摩擦角不变，模型法向黏结强度与切向黏结强度也相等。

颗粒间接触采用线性接触模型，根据试验所得应力-应变曲线、弹性模量等宏观参数，对细观参数进行反复调整标定，得到一组符合室内试验的参数值：法向接触刚度Kn=1×108N/m，切向接触刚度Ks=1×108N/m，颗粒摩擦因数μ=0.25。

4 计算结果分析

4.1 数值结果与试验结果对比分析

粗粒土试件在不同围压、压实度及含水率下三轴试验与数值模拟所得的应力-应变曲线分别如图8～10 所示[21-22]。从图8～10 可以看出：三者的应力-应变曲线变化趋势基本一致，最终差值在20%以内，由此验证了最终标定的细观参数的准确性及合理性。

图8 不同围压下粗粒土应力-应变曲线Fig.8 Stress-strain curves of coarse grained soil under different confining pressures

图9 不同压实度下粗粒土应力-应变曲线Fig.9 Stress-strain curves of coarse grained soil under different degrees of compaction

图10 不同含水率条件下粗粒土应力-应变曲线Fig.10 Stress-strain curves of coarse-grained soil under different moisture contents

由图8 可知：不同围压下粗粒土试件的应力-应变曲线变化规律相似，其力学特性均表现为应变硬化，变形分为2 个阶段即弹性阶段(εa＜1.3%)和塑性阶段(εa≥1.3%)；围压越大，试件越早进入塑性阶段，其弹性阶段的曲线斜率越大。3种围压下试验曲线最大轴应变对应的最大偏应力分别为2.21，2.95 和3.41 MPa，而数值模拟结果分别为2.44，2.98和3.60 MPa，产生这种误差的原因主要是颗粒粒径以及颗粒分布的影响。从细观角度分析，粗粒土试件在剪切过程中随着围压增大，颗粒间咬合作用增强，限制颗粒发生翻越及滚动，达到与低围压相同的变形时需要更大的偏应力。

由图9 可知：不同压实度下粗粒土试件的应力-应变曲线变化规律基本一致，偏应力峰值随着围压的增大而增大，其中，对于压实度为91%的粗粒土试件，当应变率为5.3%时，试件偏应力峰值约为1.71 MPa；对于试件压实度为94%和96%的试件，当应变率达到5.3%时，偏应力峰值约为2.25 MPa 和2.61 MPa。出现以上现象的主要原因是：压实度为94%和96%的试件较接近密实状态，而压实度为91%的试件在制作压实过程中未达到规范要求的压实度，导致其颗粒之间存在较大空隙，随着荷载次数增加，颗粒重新排列，细小颗粒更易被挤压，重新排列现象更加突出[23]。

由图10 可知：不同含水率下粗粒土试件应力-应变曲线变化较明显，其中，含水率为6.8%的试件随着偏应力增加，试件的应变率也逐渐增加；对于含水率为9.5%的粗粒土试件，试验结果显示当轴向应变达到5.13% 时，偏应力最大为1.44 MPa，而数值计算结果显示试件偏应力达到峰值时，为1.51 MPa，此时，对应的轴向应变为5.35%，之后剪切阶段试件变形所需偏应力逐渐降低，变形逐渐增大，这主要是高含水率条件下粗粒土试件易发生横向变形所致。

4.2 黏结破坏数量变化分析

黏结破坏是指采用离散元软件模拟试件剪切过程中，当颗粒间作用力大于设定黏结强度时，颗粒间的接触出现断裂破坏。离散元中颗粒的黏结破坏数量会随着剪切试验的进行而逐渐增加。通过分析黏结破坏数量变化，可从细观角度定量揭示试件轴向应变与围压、压实度及含水率的关系。

不同围压、压实度及含水率下黏结破坏数量与轴向应变之间的变化关系分别如图11～13所示。由图11 可知：在不同围压下，颗粒间黏结破坏数量增长趋势具有相似性，在高围压下，试件的黏结破坏点出现较早，应变约为0.25%时黏结破坏已出现；在低围压下，试件因体积缩小而增加的强度小于因黏结破坏而减小的强度，试件表现为应变软化；在高围压下，试件由剪切而产生的强度增加量大于黏结破坏产生的强度减小量，表现为应变硬化。由图12 可知：压实度越大，其黏结破坏点出现越早，当压实度为91%时，黏结破坏点在应变为1.8%时出现，但试件在不同压实度下的黏结破坏数量增长趋势具有相似性。由图13可知：在高含水率下，试件的黏结破坏点较靠前，对于含水率为9.5%的试件，当轴向应变为0.3%时，黏结破坏点出现；对于含水率为6.8%的试件，当黏结破坏点出现时，所对应的轴向应变为1.5%。

图11 不同围压下黏结破坏数量Ncrack随应变εa的变化关系Fig.11 Relationship between number of bond failures and strain under different confining pressures

图12 不同压实度下黏结破坏数量Ncrack随应变εa的变化关系Fig.12 Relationship between number of bond failures and strain under different degrees of compaction

在初始阶段，试件黏结破坏数量增长趋势较缓，随着轴向应变增大，试件中黏结破坏数量快速增长，当增加到一定数量后趋于平缓。出现以上现象的主要原因是：颗粒间的黏结破坏具有滞后性，颗粒所受到的外力大于黏结强度时会发生黏结破坏，这也导致试件中先出现微小变形后才出现黏结破坏；试件在剪切过程中，首先是试件的中间部位发生挤压，出现少量黏结破坏点，但该阶段试件基本能够保持原本状态；随着剪切的继续进行，试件由分散的黏结破坏点演变为连续的剪切面，其中，当连续的剪切面还未完全出现时，试件中黏结破坏数量剧增；在连续剪切面出现后，试件中黏结破坏数量增长缓慢，此时颗粒间的作用力多为残余应力。

5 结论

1)在三轴剪切试验中，试件的体应变在高围压时表现为整体剪缩，在低围压时表现为先剪缩，后剪胀；不同压实度、含水率、围压下粗粒土试件应力-应变试验曲线及数值模拟曲线变化规律基本一致。

2)当围压越高、含水率越大时，压实度越大，试件中黏结破坏点出现越早，其剪切面形成越早。

3)试件在弹性阶段，由于体积缩小而增加的强度小于黏结破坏导致的强度减小量；而在塑性阶段，试件由剪切而产生的强度增加量大于黏结破坏产生的强度减小量，颗粒间的黏结破坏具有滞后性。

4)本文仅对几种典型的围压、压实度、含水率下的粗粒土填料的力学特性及内部黏结变化进行了分析，但在工程实际中，当路基填料处于复杂的环境时，干湿循环及行车荷载都将影响路基填料的服役性能，因此，在后续研究中，应综合考虑多种因素对粗粒土填料力学性能的影响。