STABILIZATION EFFECT OF FRICTIONS FOR TRANSONIC SHOCKS IN STEADY COMPRESSIBLE EULER FLOWS PASSING THREE-DIMENSIONAL DUCTS∗
School of Mathematical Sciences,and Shanghai Key Laboratory of Pure Mathematics and Mathematical Practice,East China Normal University,Shanghai 200241,China
E-mail:hryuan@math.ecnu.edu.cn
Qin ZHAO†
Department of Mathematics,School of Science,Wuhan University of Technology,Wuhan 430070,China
E-mail:qzhao@whut.edu.cn
Abstract Transonic shocks play a pivotal role in designation of supersonic inlets and ramjets.For the three-dimensional steady non-isentropic compressible Euler system with frictions,we constructe a family of transonic shock solutions in rectilinear ducts with square cross-sections.In this article,we are devoted to proving rigorously that a large class of these transonic shock solutions are stable,under multidimensional small perturbations of the upcoming supersonic flows and back pressures at the exits of ducts in suitable function spaces.This manifests that frictions have a stabilization effect on transonic shocks in ducts,in consideration of previous works which shown that transonic shocks in purely steady Euler flows are not stable in such ducts.Except its implications to applications,because frictions lead to a stronger coupling between the elliptic and hyperbolic parts of the three-dimensional steady subsonic Euler system,we develop the framework established in previous works to study more complex and interesting Venttsel problems of nonlocal elliptic equations.
Key words Stability;transonic shocks;Fanno flow;three-dimensional;Euler system;frictions;decomposition;nonlocal elliptic problem;Venttsel boundary condition;elliptic-hyperbolic mixed-composite tpe
1 Introduction
This article is a continuation of previous works[1–8]on a systematic investigation of the existence,stability,and uniqueness of transonic shocks(that is,normal shocks)in steady com-pressible Euler flows.The study of steady compressible flows in a nozzle has attracted many authors(see,for example,[9–14]and references therein),not only because of its important applications to supersonic inlet and ramjet(see,for example,[15,Chapters 3,11]),but also the difficulties it involved in mathematics,such as free boundary,nonlinear equations of elliptichyperbolic composite-mixed type.Interestingly,although transonic shocks could be observed in experiments in a seemingly rectilinear duct(see,for example,photograph 225 in[16]),the previous mathematical studies shown that transonic shock solutions to the steady compressible Euler system in straight ducts are not stable under perturbations of the back pressures posed at the exits,or the up-stream supersonic flows(see,for instance,[1,3,7]).
To solve this paradox,many authors considered geometric effects.For the two-dimensional outward cylindrical full compressible Euler flows,the stability of transonic shocks was shown in[5],where the authors discovered many interesting nonlocal elliptic problems coming from interactions of the elliptic part and hyperbolic part of the steady subsonic Euler system.The case of Euler flows in two-dimensional divergent nozzles was well studied in[12].For a“nonisentropic potential flow model”proposed by Bae and Feldman,the stability of transonic shocks in divergent nozzles was proved in[11].For the more difficult three-dimensional steady compressible Euler flows,in[8]the authors established the stability of outward spherical transonic shocks.These works demonstrate that geometry(expanding of area of the flow tube)has a stabilization effect on transonic shocks.In a previous article[17],we considered steady subsonic compressible Euler flows in a duct with frictions.In that work,we also shown the existence of a family of special transonic shock solutions by considering fluid flows only in the axial direction of the ducts,and the frictions acting on the axial direction opposite to that of the flow.It is natural to ask whether friction,which is considered as an important factor in engineering for nozzle flows,has a stabilization effect on transonic shocks.This is exactly the purpose of this work,which is devoted to partially solving the paradox mentioned above.
The main difficulties of studying stationary transonic shocks come from the facts that the full compressible Euler equations of steady subsonic flows consist of a nonlinear system of conservation laws of elliptic-hyperbolic composite-mixed type,and the shock-front is a free-boundary.In[8],the authors established a framework to decompose the steady Euler system,as well as the Rankine-Hugoniot jump conditions,that works in a general product Riemannian manifold.The Euler system is rewritten as four transport equations plus a second-order elliptic equation of pressure,for them the lower-order terms are coupled.In this article,although general tools from differential geometry are not necessary,a single friction term changes drastically the behavior of solutions of Euler system,and lead to a stronger coupling of the elliptic parts and hyperbolic parts mentioned in[17].So,although many expressions in this article look quite similar to those appeared in[8],there are some major differences in details,and we need to treat more general Venttsel problems of nonlocal elliptic equations.
We remark that there are also many works on transonic shocks and frictional flows in the time-dependent case,but mainly on the so-called quasi-one-dimensional model,which is a hyperbolic system of balance laws;see for example,[18–23]and references therein.If the friction forces depend linearly on momentum,one may also consult[24,25]and references therein for large time behavior of weak solutions.
In the rest of this section,we formulate the transonic shock problem(T),and state the main result of this article,namely Theorem 1.3.In Section 2,we reformulate problem(T)by using a decomposition of the system(1.1)–(1.3)established in[8].In Section 3,we study a crucial Venttsel boundary-value problem for a second-order nonlocal elliptic equation.In Section 4,by showing contraction of a nonlinear mapping,we prove Theorem 1.3.
1.1 The transonic shock problem
We now formulate the transonic shock problem in a more technical way.As in all of the previous works,we consider polytropic gases:
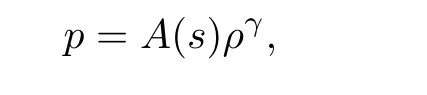

In the Descartesian coordinates(x0,x1,x2)of the Euclidean space R3,let D={(x0,x1,x2):x0∈ (0,L),(x1,x2)∈ (0,π)×(0,π)}be a rectilinear duct with length L and constant square cross-section,where the gas flows along the positive x0-direction.Hence,we call the entry of the duct D0={(x0,x1,x2):x0=0,(x1,x2)∈ (0,π)× (0,π)}and the exit of the duct DL={(x0,x1,x2):x0=L,(x1,x2) ∈ (0,π)× (0,π)},respectively.To avoid technical difficulties arose by the lateral walls,as in[3,9,26,27],by assuming the upstream supersonic flows and the back pressures have some symmetric properties with respect to the walls[0,L]× ∂[0,π]2,we may suppose the flows are periodic in x1,x2-directions with periods 2π.The details are presented in[3,p.528,p.552],so we omit them here.
Let u=(u0,u1,u2)⊤be the velocity of the gas flows.Recall that the flow is called subsonic at a point if the Mach numberand supersonic if M>1.Then as explained in[17],the motion of compressible Euler flows with frictions is governed by the following equations([28–30]):

where ‘div’and ‘grad’are,respectively,the standard divergence and gradient operator in R3;is the so-called Bernoulli function(which is total enthalpy per unit mass of gas),andrepresents the force of friction acting on per unit mass of gas with a positive constant µ.These equations are the conservation of momentum,mass,and energy,respectively.

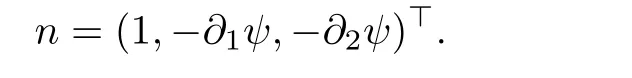
Definition 1.1(Transonic shock) LetandWe say that U=(U−,U+;ψ)is a transonic shock solution,if
1)U±solve the system(1.1)–(1.3)inin the classical sense;
2)U−is supersonic,and U+is subsonic;
3)The following Rankine–Hugoniot jump conditions(R–H conditions)hold across Sψ:

where u·n is the standard inner product of the vectorsanddenotes the jump of a quantity f(U)across Sψ;
4)There holds the following physical entropy condition

By the definition we infer that a transonic shock solution is a weak entropy solution of the steady Euler system(1.1)–(1.3)(Section 4.3 and Section 4.5 in[30]).
To formulate the transonic shock problem,we need to specify boundary conditions,which are similar to the previous works.Because the flow U−is supersonic near the entry Σ0,we shall propose the following Cauchy data:

On the exit Σ1,from considerations in engineering,as in the studies of subsonic flows,we require that

where p1is a given function defined on T2.
Problem(T)Find a transonic shock solution in Ω which satisfies the boundary conditions(1.9)and(1.10)pointwisely.
1.2 Main result
The existence of a family of special transonic shock solutionswith the position rbof the shock(which are called as background solutions in the sequel)to Problem(T)has been established in[17].Recall that the background solutions Ub,which depend only on x0,satisfy the following ordinary differential equations(see(2.2)–(2.4)in[17]):

Remark 1.2For given L less than a maximal length,for which the flow at the exit is still subsonic,by the theory of ordinary differential equations,we note thatactually depends analytically on the parameters γ >1,µ ≥ 0,rb∈ [0,L],andIn addition,it is important to note that the subsonic Fanno flowcould be extended analytically tovia these equations,for a small positive constant hbdepending solely on these parameters.
We may also imagine that the exit{x0=L}lies on the left-hand side of the shock-front,namely,rb>L but close to L:The flow is supersonic on 0≤x0≤rb, flows from left to right,and jump to subsonic at rb,then flows to the left(for x0 In this article,we are mainly concerned about the existence of general transonic shock solutions that are obtained by multidimensional perturbations of background solutions.The main theorem is stated as follows. Theorem 1.3Suppose that a background solution Ubsatisfies the S-Condition(see Remark 1.4 below),and α ∈ (0,1).There exist ε0>0 and C∗>0 depending only on Uband γ,α,L,such that if the upcoming supersonic flowonand the back pressure p1on Σ1satisfy Furthermore,such solution is unique in the class of functions ψ,U−,U+with Remark 1.4The technical S-Condition is given by Definition 3.2 in Section 3.It is shown there that a large class of background solutions Ubsatisfy the S-Condition. Remark 1.5The existence and uniqueness of supersonic flow U−in Ω =(0,L)×T2subjected to the initial datasatisfying(1.12)follow from the theory of semi-global classical solutions of the Cauchy problem of quasi-linear symmetric hyperbolic systems if ε0is sufficiently small(depending on L,[31]).Furthermore,there exist C0>0 depending solely on(0)and L,such that which implies(1.15).So,Problem(T)is indeed a one-phase free-boundary problem,for which the free-boundary(that is,the shock-front)Sψand the subsonic flow U+are to be solved.For simplicity,from now on we write U+as U. The following is an important theorem established in[8,p703]),which is rewritten for use to our case,namely,is now a flat manifold.So,for a vector field u,we have Du=u ·grad.As a convention,repeated Roman indices will be summed up for 0,1,2,while repeated Greek indices are to be summed over for 1,2,except otherwise stated. and the boundary condition on Sψ: Here,L0(·)is a linear function,and Lk(·),Lk(·)are smooth functions so that Lk(0)=0,Lk(0)=0 for k=1,2,3. To formulate a tractable nonlinear Problem(T1)which is equivalent to Problem(T),we need to compute the exact expressions of(2.3)and(2.5),then specify the auxiliary functions Lk,Lkappeared in Proposition 2.1. We now compute the explicit expression of equation(2.3).It is straightforward to check that where and δkjis the standard Kronecker delta.Replacing terms likein(2.6)by using suitable equations(1.1)–(1.3)(this is why we introduced Lk),after some straightforward computations,we obtain the identity with Multiplying γp to both sides of(2.8),and comparing it with(2.3),we see that(2.3)is equivalent to the following second order equation of pressure: Setting we have the identity Comparing this to(2.5),it is a nonlinear Robin condition for p on Sψ: with By the definition of shock-front,the mass flux(otherwise it is called as a contact discontinuity).So,from(1.6)and(1.7),we infer thatwhile(1.6)and(1.7)may be written as The conservation of momentum(1.5)shall be decomposed as If[p]>0(which is guaranteed by the physical entropy condition satisfied by the background solution,and the small perturbation estimate(1.16)to be established),from(2.17)we solve that with Thus,the R-H conditions(1.5)-(1.7)are equivalent to(2.15),(2.16),and(2.18),if Remark 2.2By(2.18),it is necessary that,which implies On the contrary,because the first Betti number ofis 2,by deRham’s Theorem and Hodge Theorem,(2.19)–(2.21)are also sufficient for the existence of a unique function ψponso that(2.18)holds,andThe function ψpis called the pro file of the surface Sψdefined by(1.4),and the constantis called the position of Sψ.As known from previous works in[8],ψpis determined by R-H conditions,while rpis determined by an integral-type solvability condition derived from the Euler equations.We note that conditions like(2.20)and(2.21)do not appear in the cases of spherical symmetric flows considered in[8,p.730],which exhibit the significant influences of topology in the studies of transonic shock problems. In this subsection,we separate the linear parts from the nonlinear equations(2.1),(2.10),(2.12),and the R–H conditions(2.15),(2.16),and write them in the form where L is a linear operator,andconsist of certain higher-order terms defined below. Definition 2.3LetA higher-order term is an expression that contains either 2.4.1 Linearization of Bernoulli law Recall that for the background solution,Bbsolves the equationSo,we have the identity Using the expressions like where O(1)represents a bounded quantity with a bound depending only on the background solution Uband|U−Ub|,and after straightforward calculations,(2.1)is equivalent to where 2.4.2 Linearization of pressure’s equation We easily see that(2.26)is an elliptic equation of(perturbed)pressure for subsonic flow.The coefficients in(2.26)are given by and 2.4.3 Linearization of boundary condition Note that(2.12)is equivalent to which could be written as with γ0determined by the background solution: and 2.4.4 Linearization of R-H conditions Next,we linearize the R–H conditions(2.15)and(2.16).Letand V−=Then,we write them equivalently as with As in[6,p.2522],using the fact that By the Taylor expansion formula,all the five terms in Iiare of higher-order for i=1,2,3,while it is not the case in for i=1,2,3.We remark that this is quite essential for the stabilization of transonic shocks.Actually,using(1.11)and the result obtained by direct calculations,(2.33)equals to We can solve these linear algebraic equations to have Using A(S)=pρ−γ,it also holds that where and gk(k=1,2,3,4)are higher-order terms.Observing that if the friction disappears,namelyµ=0,then all the coefficients above are zero,and there is no couplings in equations(2.34)-(2.36)on the position of shock-front.This is one of the key point why friction may have a stabilization effect on transonic shocks. From(2.35)and(2.37),we also have 2.4.5 Divergence of tangential velocity field on shock-front Now,we restrict(2.29)on Sψ.So,particularly x0should be replaced by ψ.Using the commutator relation for a function f defined on Ω: we have and Similarly,one may replace the normal derivatives by tangential derivatives to computeand.Then,(2.29)becomes Here,γ1<0,γ2<0 are constants determined by the background solution,and We see that(2.40)is equivalent to Remark 2.4As observed in[8,p.728],in the expression of g5,there appear first-order derivatives of,and only first-order tangential derivatives of A(s),u′,B,ψ on Sψ.Also,(2.42)is a first-order boundary condition on the shock-front.Together with(2.19),we have a div-curl system of the tangential velocityon 2.4.6 Problem(T1) For functions U=(B,A(s),p,u′)and ψ(note thatandwe formulate the following problems: It is obvious now that for given supersonic flow U−,the solution(U,ψ)to these problems also solves the Euler system,and the R-H conditions hold across Sψ.Hence,we rewrite Problem(T)equivalently as the following Problem(T1). Problem(T1)Find ψ and U=U+insatisfying(1.14),(1.16)and solving the problems(2.43)–(2.47). Acting the divergence operator to the first equation in(2.46)and using the second equation,we derive that Then,using the third equation in(2.44),we have Substituting this into the third equation in(2.44),we then obtain We now formulate the following Problem(T2),which is equivalent to Problem(T1)([8,p730]). Problem(T2)Find ψ andthat solve(2.43),(2.52),(2.53),(2.45),(2.54),and(2.47). The above equations and boundary conditions are formulated in.Supposing ψ ∈C4,α(T2),we introduce a C4,α–homeomorphismdefined by To avoid complication of notations,in the following we still write the unknownsin y-coordinates as U etc,and write the velocity still as u.We have Here,we use i∗to denote the trace operator on Hence,Problem(T2)could be rewritten as the following Problem(T3)in the y-coordinates,where we useorto denote the corresponding higher-order terms. Problem(T3)Findandthat solve the following problems(2.57)–(2.62).The initial datain(2.62)is the vector field corresponding toonobtained from(2.61). Remark 2.5Recalling(2.26),in(2.58)we should have where the coefficients are known functions of y0,and F5=F5(U,ψ,DU,D2p,Dψ,D2ψ)is the higher-order term appeared below(2.26)in the y-coordinates,and We also note that As the elliptic problem(2.58)is coupled with the other hyperbolic problems,we need to further reformulate Problem(T3)equivalently as the following Problem(T4). We now consider the Cauchy problems(2.57)and(2.60): Here,we have replaced the boundary condition in(2.60)by(2.38),and For the vector field u defined in M,we consider the non-autonomous vector fielddefined for y′=(y1,y2)∈T2and y0∈[rb,L].Forwe write the integral curve passingwhich is a Ck,αfunction in M ifand u0>δ for a positive constant δ,and k∈N.For fixed y0,the mapis a Ck,αhomeomorphism,thenNote that ϕrbis the identity map on T2.Also,recall the following lemma appeared in[8,p.733]: Lemma 2.6Suppose that u=(u0,u′) ∈ C0,1and u0> δ.There is a positive constant C=C(δ,L)so that for any y′∈ T2and y0∈ [rb,L],it holds that We write the unique solutions to the linear transport equations(2.65)and(2.66)respectively as: Because the entropy is a constant behind the shock-front for the background solution,we have Now,set which are higher-order terms(note thatand∂βA(s)are small,andis close to the identity map because u′is nearly zero,sois small by(2.67)).Then,we could write the elliptic equation(2.63)as If we define then equation(2.74)simply reads We then state Problem(T4),which is equivalent to Problem(T3),as can be seen from the above derivations. Problem(T4)Findanddefined in M that solve problems(2.57),(2.76)and(2.59)–(2.62). To attack problem(2.76),we study in this section the following linear second-order nonlocal elliptic equation subjected to a Venttsel boundary condition on M0: In 1959,A.D.Venttsel proposed the now called Venttsel problem of second-order elliptic equations[32],from the view point of probability theory.A survey of the mathematical studies of Venttsel problem could be found in[33].It is quite interesting to see that such Venttsel problems appear so naturally in the studies of transonic shocks,not only for the geometric effects considered in[8],but also the effects of frictions considered in this article.As we mentioned in[8],the linear theory established by Luo and Trudinger in[34]cannot be applied directly to our problem,because the elliptic operatorcontains nonclassical nonlocal terms,and the coefficients of the zeroth-order term may change sign.So,in the following,we mainly follow the procedure in[8]to study problem(3.1). We firstly study,under what conditions,that a strong solutionin Sobolev space H2(M)withto problem(3.1)is unique.To this end,we consider the homogeneous problem Lemma 3.1(Regularity)Ifwithis a strong solution to(3.2),thenis a classical solution and belongs to We wish to find some conditions to guarantee thatThe idea is to use the method of separation of variables via the Fourier series.Similar to[17],denote m=(m1,m2),then by the above lemma,we could write where For y=(y0,y1,y2),the coefficients in(3.3)are given by Substituting(3.3)into(3.2),for y0∈[rb,L],each pi,m(y0)solves the following nonlocal ordinary differential equation subjected to the two-point boundary conditions: We need to find sufficient conditions so that all pi,m(i=1,2,3,4)are zero. Here,we define Then,it solves Definition 3.2We say that a background solution Ubsatisfies the S-Condition,if for each i=1,2,3,4,and m∈Z2,problem(3.7)does not have a classical solution. If the background solution Ubsatisfies the S-Condition,then all pi,mare zero,hence problem(3.2)has only the trivial solution.Recall that a background solution is determined analytically by the following parameters:Our purpose below is to show theoretically that almost all background solutions satisfy the S-Condition.Actually,we have the following lemma. Lemma 3.3Suppose that the Mach number of the background solution satisfies t(y0) where We recall that the background solution Ub,and all the coefficients e1,e2,e3,e4,as well as b,depend analytically on rb.Hence,the unique solutionto this Cauchy problem(3.9)(exclude the last condition)is also real analytic with respect to the parameter rb[36].We write it asParticularlyis continuous for rb∈ [0,L],and real analytic for rb∈[0,L). It is crucial to note that there is an analytical continuation ofup to the point rb=L.This follows from the observation in Remark 1.2,by which all the coefficients,nonhomogeneous terms,and boundary conditions in(3.9)make sense for rb>L(but close to L),and are actually analytic for rbin a neighborhood of L. Applying Theorem 8.12 in[35,p.186]to the boundary equation in(3.1),we have By considering the nonlocal terms Then,by(3.11)and a compactness argument as in[8,p.738],we deduce the a priori estimate provided that the S-Condition holds.Here,the constant C depends only on the background solution. with C a constant depending only on the backgroundsolution Uband L,α.Then by an argument similar to the proof of(3.12),we have the a priori estimate: for any Ck,αsolution of problem(3.1),provided that the only solution to problem(3.2)is zero. We now use Fourier series to establish a family of approximate solutions to problem(3.1). Without loss of generality,we take h1=0 in the sequel.We also setto be a sequence offunctions that converges to f inandconverges to h0inNow for fixed n,we consider problem(3.1),with f there replaced by f(n),and h0replaced by Suppose that We will show that this problem is uniquely solvable. For any real numbers c1,c2, solves the Cauchy problem Therefore,to solve problem(3.17),there shall exist c1,c2to solve the following linear algebraic equations:In fact,we know that,under the S-Condition,the homogeneous system has only the trivial solution.So,by Fredholm alternative of linear algebraic equations,there is one and only one pair(c1,c2)solving the above linear system,which enables us to obtain the unique solution to problem(3.17). Now for N∈N,we define By estimate(3.12),for any N1,N2∈N with N1 Now,for the approximate solutions,we use estimate(3.14)to infer that Hence,by Ascoli–Arzela Lemma,there is a subsequence ofthat converges to somein the norm of.Taking limit with respect to this subsequence in the boundary value problems of,we easily see thatis a classical solution to problem(3.1).Therefore,we proved the following lemma. Lemma 3.4Suppose that the S-Condition holds.Then,problem(3.1)has one and only one solution in,and it satisfies estimate(3.14). We now use a Banach fixed-point theorem to solve the transonic shock problem(T4),provided that the background solution Ubsatisfies the S-Condition. Let σ0be a positive constant to be specified later,and be the set of possible shock-front.For any givenits position rpand pro file ψpalso satisfy We write the set of possible variations of the subsonic flows as The constants σ0,δ0will be chosen later.For k=2,3,the normappeared here is defined by Given U−satisfying(1.21),for any ψ ∈Kσandwe construct a mapping as follows.One should note that a fixed-point of this mapping is a solution to Problem(T4).We also use C to denote generic positive constants which might be different in different places. PressurepWe first consider problem(2.76)on: Here,the non-homogeneous terms F andare determined by ψ ∈Kσandwith,and−is solved from(1.21).Then,because we assumed that the S-Condition holds,by Lemma 3.4,we could solve uniquely oneand it satisfies the following estimate: Checking the definitions of F andwe have So,combining(1.21),(1.13)and(4.2),(4.3),one infers that Update shock-frontWith the specified higher-order termsand,andsolved from(4.1),we now set(cf.(2.59)) It follows easily that(using(4.4)) For the C4,αestimate of,we note thatsolves the third equation in(4.1),hencesolves the following elliptic equation on(cf.(2.48)): Standard Schauder estimates[35,Chapter 6]yield that Hence,one has We also need to show that In fact,integrating(4.7)on T2,recallingand using divergence theorem and definition ofin(4.5),we have directly(4.10). EntropyA(s) Noting thatis constant,we solve problem(2.60) Bernoulli functionBWe then solve the linear problem(2.57)on: Hence,we could easily establish the unique existence of(note thatwith The estimate(1.21)is used to obtain the second inequality. Tangential velocity fieldonM0Next,we solve the tangential velocityon M0from(2.61) By applications of deRham’s Theorem and Hodge Theorem,or treated as in[3,p546–547],one can solve a uniqueon T2,and the following estimate is valid: Tangential velocityinMFinally,we solve the tangential velocityû′in M through(cf.(2.62)) From(4.4)and(4.16),we obtain a uniquein M and it holds that ConclusionFrom the above six steps,we obtain uniquely one pairand it follows from(4.4),(4.9),(4.12),(4.14),(4.16),and(4.18)that and estimate(4.19)shows thatand.Hence,we construct the desired mapping T on What left is to show that the mapping is a contraction in the sense that provided that ε0is further small(depending only on the background solution and L,α).Here for j=1,2,and anywe have defined Step 1Firstly we seek an estimate of ep,which solves(4.1) Here,for k=1,2, By Lemma 3.3 and(4.21),direct computation yields Step 2From(4.5),we see that Here,for k=1,2, Then,we have the following estimate via(4.24)and some straightforward computations: with it follows that,from(4.24)and(4.25), This and(4.25)imply that Step 3From(4.11),one has where By(4.23)and(4.26),we have Step 4We note thatsolves the following problem(cf.(4.13)) with Then using(4.21),(4.23),(4.24),and(4.27),one has Step 5Next,by(4.15)we find that the difference of tangential velocity field on M0solves where,for k,β=1,2, We easily deduce the estimate Step 6From(4.17),(β=1,2)solves with So,there holds ConclusionNow,summing up inequalities(4.24)–(4.30),we have which implies(4.20)if ε∈ (0,ε0)andFinally,by a Banach fixed-point theorem,we infer that Problem(T4),hence Problem(T),has one and only one solution in.This finishes the proof of Theorem 1.3.





2 Reformulation of Problem(T)



2.1 The equation of pressure





2.2 The boundary conditions


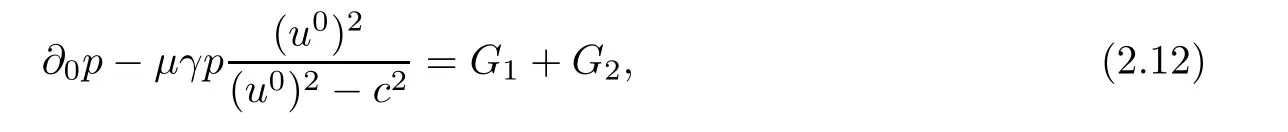

2.3 Decomposition of R-H conditions

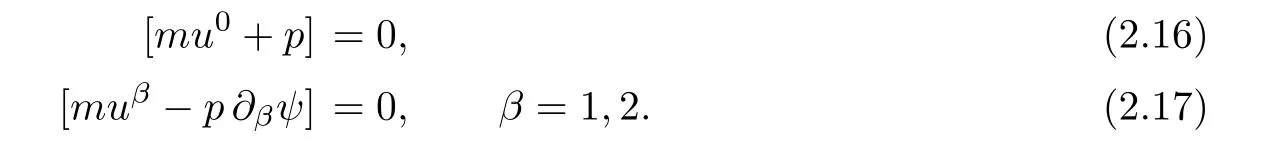




2.4 Problem(T1)


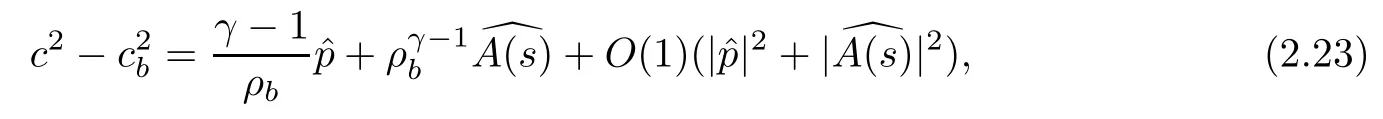


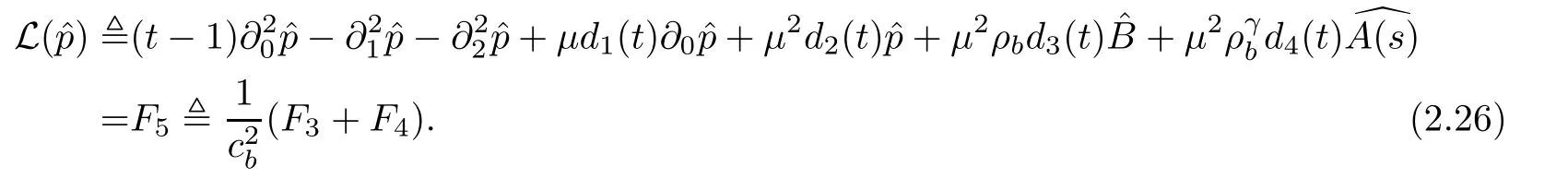













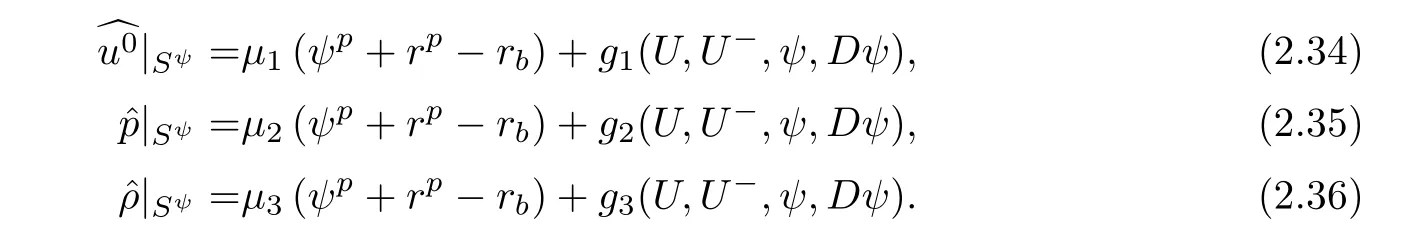

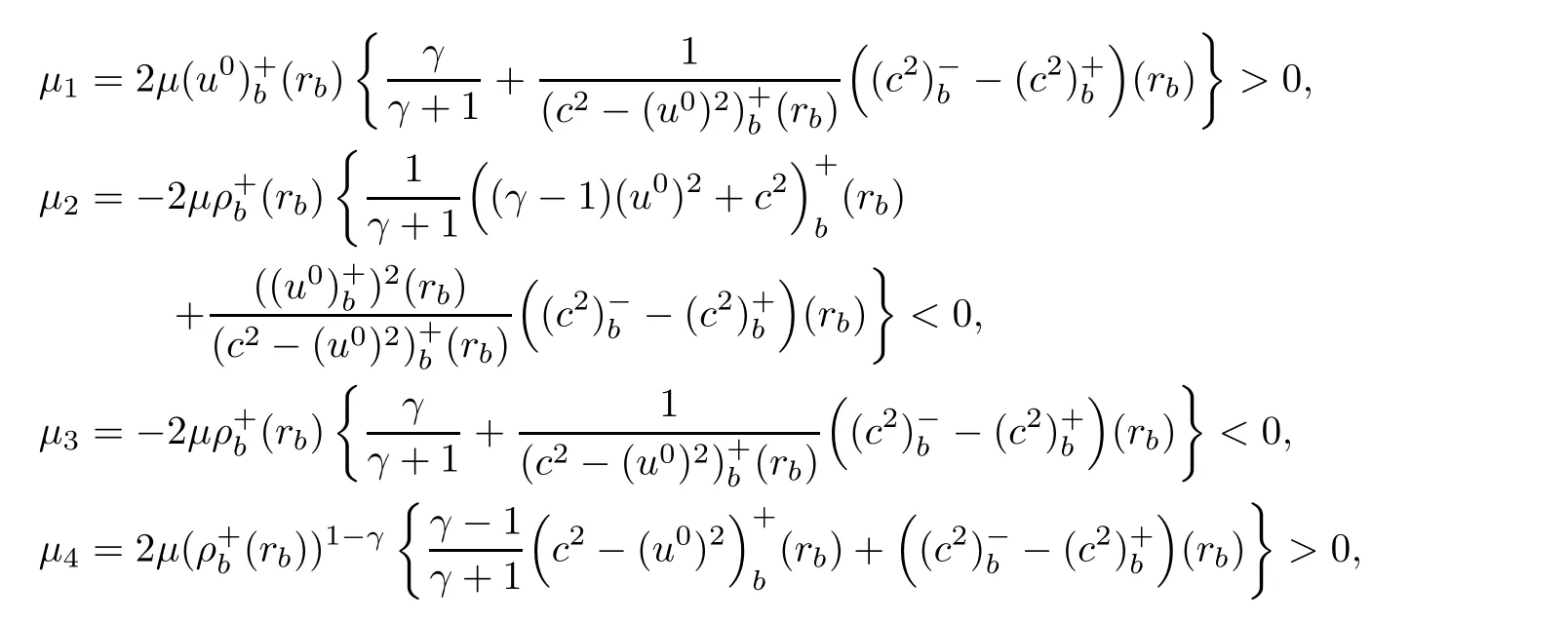










2.5 Problem(T2)





2.6 Problem(T3)







2.7 Problem(T4)
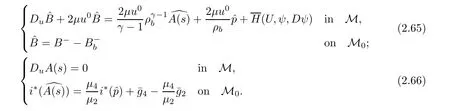
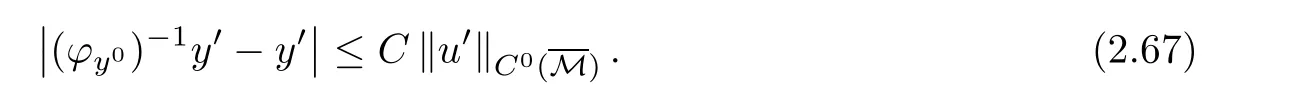









3 A Linear Second-Order Nonlocal Elliptic Eequation With a Venttsel Boundary Condition

3.1 Uniqueness of solutions in Sobolev spaces
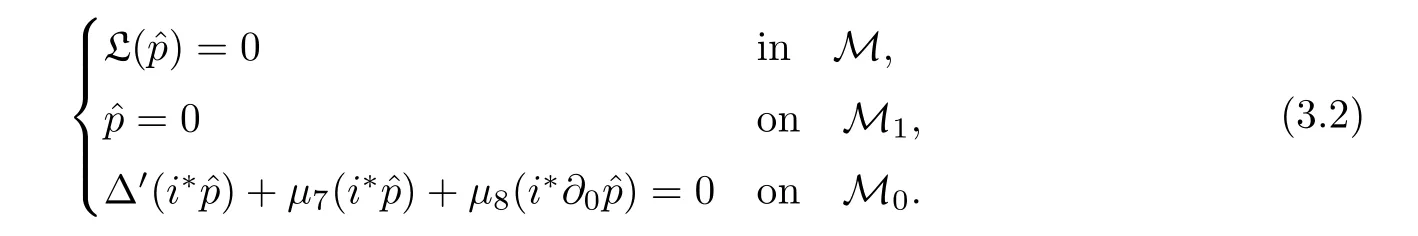







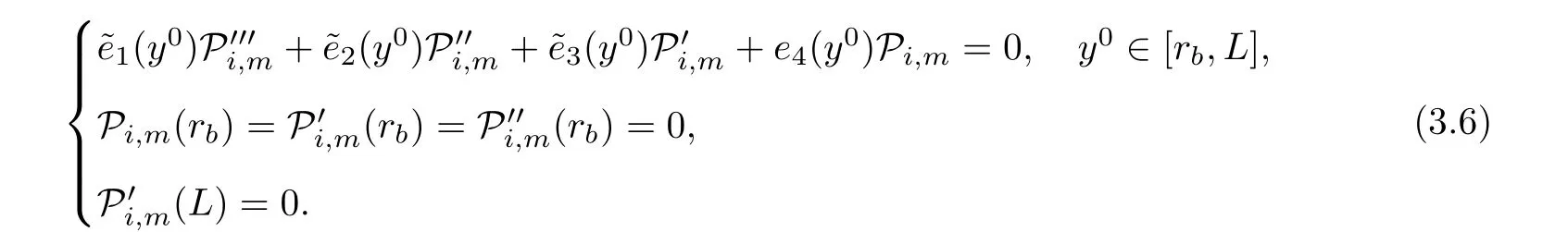





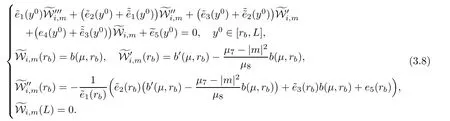




3.2 Uniform a priori estimate in Sobolev spaces


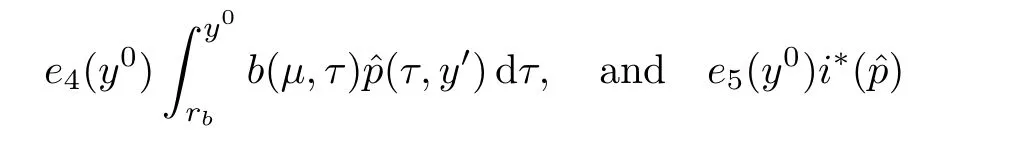



3.3 Uniform a priori estimate in Hölder spaces



3.4 Approximate solutions









3.5 Existence


4 Stability of Transonic Shock Solution
4.1 The iteration sets




4.2 Construction of iteration mapping


















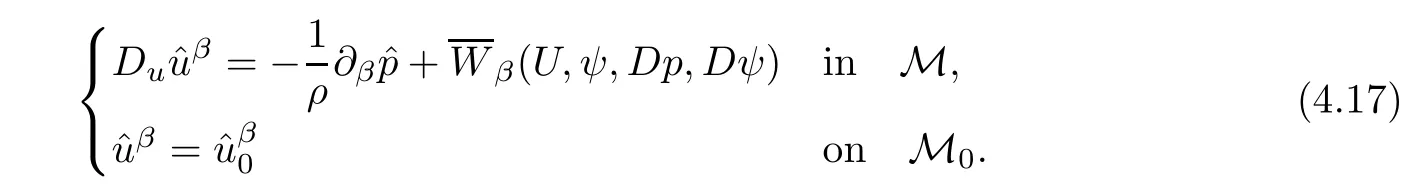




4.3 Contraction of iteration mapping






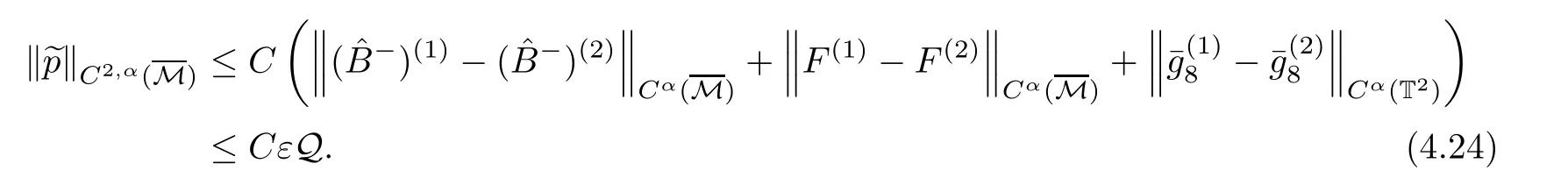


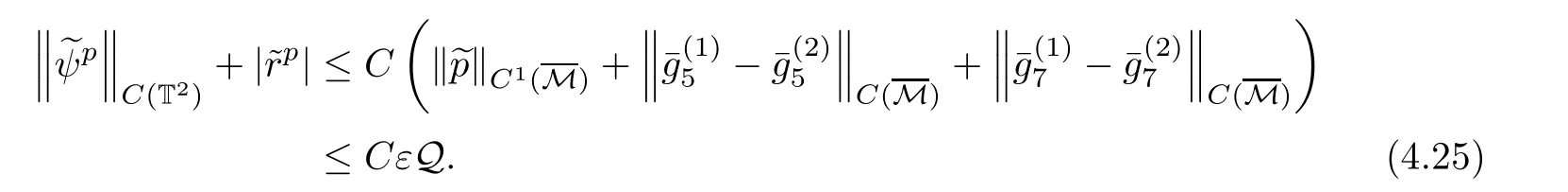

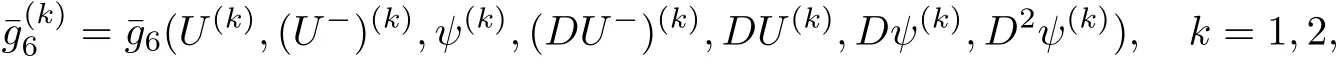
















 Acta Mathematica Scientia(English Series)2020年2期
Acta Mathematica Scientia(English Series)2020年2期
