ON THE EXISTENCE OF SOLUTIONS TO A BI-PLANAR MONGE-AMPÈRE EQUATION∗
Institut für Angewandte Analysis,Universität Ulm,89069 Ulm,Germany
E-mail:ibrokhimbek.akramov@uni-ulm.de
Marcel OLIVER
School of Engineering and Science,Jacobs University,28759 Bremen,Germany
E-mail:m.oliver@jacobs-university.de
Abstract In this article,we consider a fully nonlinear partial differential equation which can be expressed as a sum of two Monge-Ampère operators acting in different two-dimensional coordinate sections.This equation is elliptic,for example,in the class of convex functions.We show that the notion of Monge-Ampère measures and Aleksandrov generalized solutions extends to this equation,subject to a weaker notion of convexity which we call bi-planar convexity.While the equation is also elliptic in the class of bi-planar convex functions,the contrary is not necessarily true.This is a substantial difference compared to the classical Monge-Ampère equation where ellipticity and convexity coincide.We provide explicit counter-examples:classical solutions to the bi-planar equation that satisfy the ellipticity condition but are not generalized solutions in the sense introduced.We conclude that the concept of generalized solutions based on convexity arguments is not a natural setting for the bi-planar equation.
Key words Fully nonlinear elliptic equations;generalized solution;bi-planar convexity
1 Introduction
We study the fully nonlinear second order equation

on a three-dimensional domain Ω⊂R3.Setting
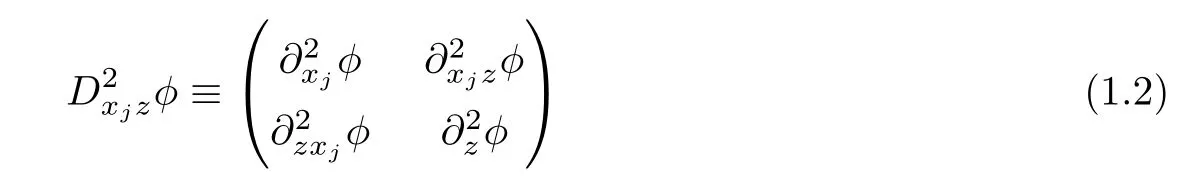
for j=1,2,we can write(1.1)in the form

Thus,the operator on the left is the sum of two planar Monge-Ampère operators on perpendicular sections.For this reason,we shall refer to(1.3)as the bi-planar Monge-Ampère equation.
The characteristic matrix(see[3])for(1.3)reads
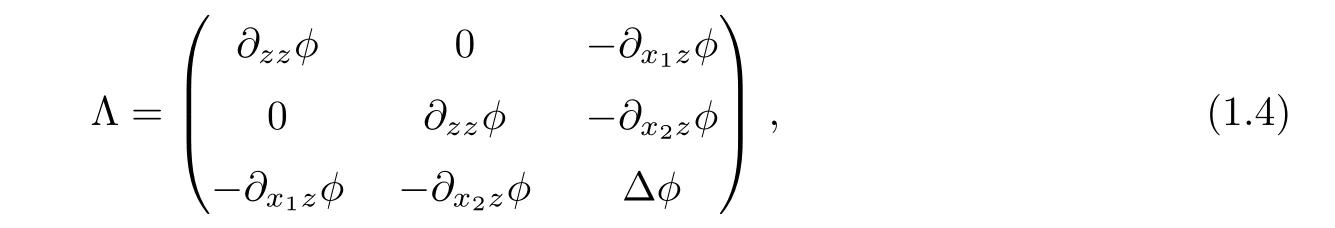
where∆denotes the Laplacian in the(x1,x2)-plane.Equation(1.3)is elliptic(in the sense of linearization)when Λ is positive definite.This is the case if and only if

In particular,(1.3)is elliptic in the class of convex functions.
The study of the bi-planar Monge-Ampère equation is motivated by a recent article[8]on variational balance models for rapidly rotating stratified fluid flow.For a class of models that includes the so-called L1-model first proposed by R.Salmon[2,10],the vertically integrated potential temperature Θ is related to the potential vorticity of the fluid via
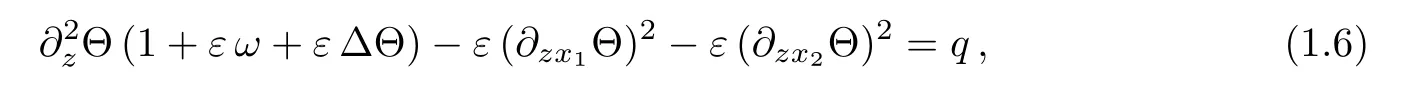
where,up to rescaling,ω = ω(x1,x2)is the vorticity of the horizontal mean flow and ε is the Rossby number.Setting

where∆−1denotes the inverse Laplacian on the two-dimensional horizontal domain U with homogeneous Dirichlet boundary conditions on∂U,we see that(1.6)can be written in the form of the bi-planar Monge-Ampère equation(1.3)on the cylindrical domain Ω=U×(0,1).In particular,(1.6)is elliptic if and only ifand q>0.
In this article,we ask the question in which sense the well-established theory of generalized solution of the classical Monge-Ampère equation[3–5]carries over to the bi-planar Monge-Ampère equation.We find that it is possible to construct a bi-planar analog of the Monge-Ampère measure which can be used to define generalized solutions and assert their uniqueness[4,5,11].For this construction,it is necessary to require that the solution is convex on the respective coordinate sections.This notion,which we term bi-planar convexity,is more general than convexity.However,it is also more restrictive than the ellipticity condition(1.5).Indeed,we show by example that there exist classical solutions to the Dirichlet problem for the bi-planar Monge-Ampère equation such that the equation is elliptic in the vicinity of these solutions;yet,these solutions are not bi-planar convex.This is in contrast to the situation for the classical Monge-Ampère equation equation,where the notions of convexity and ellipticity coincide.
It should be noted that the classical Monge-Ampère equation is closely related to the geometric notion of convexity.However,bi-planar Monge-Ampère equation is related to the property of convexity for the two planar sections.Surely,if a function is convex,so are its planar sections.The converse,however,is not true(see Remark 2.2 below).This illustrates that bi-planar convexity does not have an intrinsic geometric meaning in three dimensions.Correspondingly,convex analysis does not lead to a natural notion of solution for the bi-planar Monge-Ampère equation.
The remainder of this article is structured as follows.In Section 2,we develop the convexity based theory:We introduce the notion of bi-planar convexity,define the bi-planar Monge-Ampère measure,prove monotonicity and a comparison principle,and finally use these notions to define the bi-planar analog of Aleksandrov generalized solutions.Section 3 is devoted to counter-examples which show that there is a gap between the concept of convexity,or even bi-planar convexity,and ellipticity for associated Dirichlet problem.This article concludes with a brief discussion.
2 Bi-Planar Monge-Ampère Measure
2.1 Construction
We define a measure on the Borel σ-algebra of R3,the bi-planar Monge-Ampère measure,by using planar Monge-Ampère measures on sections,then integrating over the remaining dimension.We begin the construction by defining a weaker notion of convexity adapted to the bi-planar structure of our equation.
Definition 2.1Let φ be a continuous function defined on the set Ω ⊂ R3.The function φ is bi-planar convex if for any fixed x1and x2,φx1(x2,z) ≡ φ(x1,x2,z)and φx2(x1,z)≡φ(x1,x2,z)are convex functions on the respective sections

and
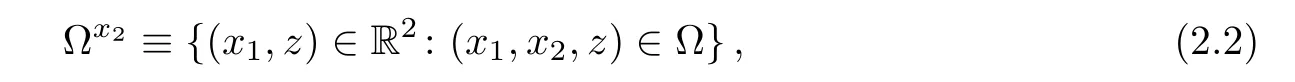
whenever these are nonempty.
Remark 2.2A convex function is bi-planar convex,but the converse is not necessarily true.For example,

is bi-planar convex but not convex.
For the classical Monge-Ampère equation on a domain Ω⊂Rn,

where ν is a given Borel measure on Ω,an Aleksandrov generalized solution is a convex function φ∈C(Ω)such that Mφ=ν,where Mφ denotes the Monge-Ampère measure

for every Borel set E ⊂ U.Here,∂φ is the normal map or sub differential defined at a point x∈Ω by

and for a Borel set E⊂Ω by

The Monge-Ampère measure(2.5)relates to the Monge-Ampère equation(2.4)via the identity
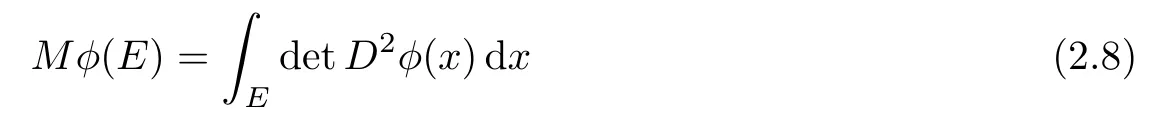
for all Borel sets E ⊂ Ω,which holds true whenever φ ∈ C2(Ω);see,for example,[4]for details.Derivatives of generalized solutions exist generally only in the sense of sub differentials but,being convex,generalized solutions have classical derivatives of second order a.e.[1].
In the following,we mimic this correspondence for the bi-planar Monge-Ampère equation.Suppose that Ω ⊂ R3is open andis bi-planar convex.For every x1∈ R,we define the measureon Ωx1as the planar Monge-Ampère measure associated with the convex continuous function φx1;when Ωx1is empty,we take this measure to be zero.Likewise,for every x2∈ R,we define the measure M13φx2on Ωx2as the planar Monge-Ampère measure associated with φx2.
When E=E1×E23⊂Ω is compact with E1⊂R and E23⊂R2,thenµx1(E23)≡M23φx1(E23)is continuous on E1by[4,Lemma 1.2.3].We can thus Lebesgue-integrate over E1and define
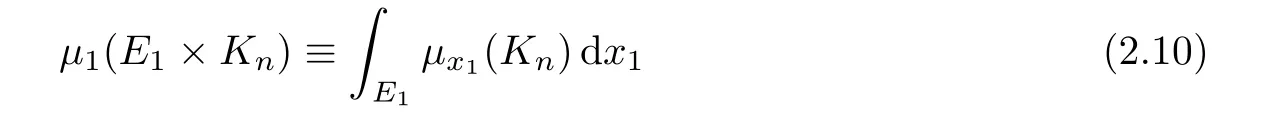
is increasing,and

is Lebesgue measurable on E1.Hence,by the monotone convergence theorem,

is well-defined.Because of the countable additivity of the Monge-Ampère measure and countable additivity of the Lebesgue integral,µ1defines a pre-measure which can be extended to a Borel measure on Ω.
Analogously,we define a measure µ2corresponding to the function φx2.Finally,the biplanar Monge-Ampère measure is defined as

2.2 Basic properties
We now provide the basic characterization of the bi-planar measure associated with smooth functions and prove monotonicity of the measure.
Lemma 2.3Ifis bi-planar convex,then µφis absolutely continuous with respect to the Lebesgue measure and
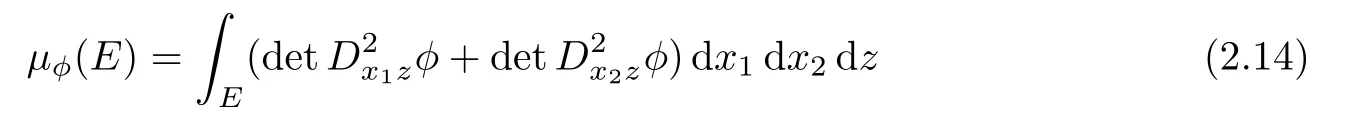
for all compact E⊂Ω.
ProofWe will show that

Because of the properties of the Lebesgue measure,it suffices to prove this relation for cylindrical sets of the form E=E1×E23⊂ Ω;an arbitrary compact E ⊂ Ω can be approximated by a union of such sets.
By[4,Example 1.1.14],we have

Hence,by definition(2.12),we have

Similar arguments show that
Combining(2.15)and(2.18),we complete the proof.
Lemma 2.4Let Ω ⊂ R3be open and bounded,and letbe bi-planar convex.If φ = ψ on ∂Ω andin Ω,then for any fixed y1∈ R and y2∈ R,
ProofThe strategy of proof closely follows[4,pp.10–11].We write out the argument for(2.19a)explicitly;the proof of(2.19b)is analogous.

for all(x2,z) ∈ Ωy1.Subtracting φy1(x2,z)from(2.20),taking the supremum on the right hand side,and using that ψy1≥ φy1,we find that

As Ω and Ωy1are bounded and φy1is continuous,the supremum in(2.21)is attained at someso that,by the definition of a,

for all(x2,z)∈ Ωy1.Clearly,the right hand side of(2.22)defines a supporting hyperplane forWhenwe conclude thatand we are done.Otherwise,when,then,by assumption,.Furthermore,by continuity of ψ,we may letin(2.20),so that
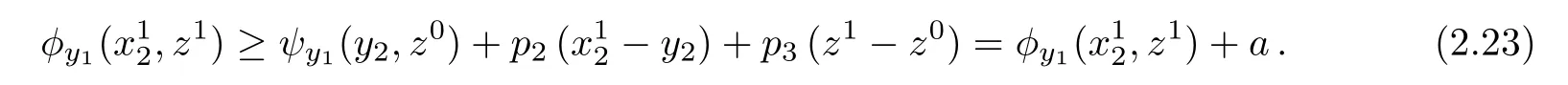
As a≥ 0,this implies a=0.Therefore,By assumption,the reverse inequality is also true,so thatWith these provisions,the first line in(2.22)reads

Clearly,the right hand side defines a supporting hyperplane for φy1at(y2,z0),so that(p2,p3) ∈∂φy1(Ωy1)in this case,too.
Lemma 2.5Let Ω ⊂ R3be open and bounded,and let φ,be bi-planar convex.If φ ≤ ψ in Ω and φ = ψ on ∂Ω,then

ProofLemma 2.4 implies,for any fixed x1,the inclusionHence,

Integrating this inequality with respect to x1,we obtainwhereandare the measures µ1corresponding to φ and ψ,respectively.
An analogous argument yieldswhereandare the measures µ2corresponding to φ,and ψ,respectively.Asthe proof is complete.
Finally,superadditivity of the Monge-Ampère measure(for example[4,p.17])directly implies the following inequality.
Lemma 2.6Let Ω ⊂ R3be open and bounded and let φ,ψ ∈ C(Ω)be bi-planar convex functions.Then

for any Borel set E⊂Ω.
2.3 Comparison principle
The first central result which carries over from the classical Monge-Ampère measure to the bi-planar case is the comparison principle.The proof is a close adaptation of[4,pp.16–17].
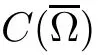

Then
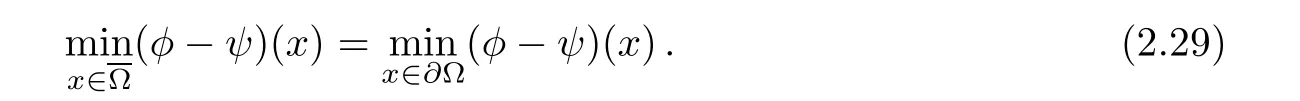
ProofSuppose that(2.29)does not hold,that is,

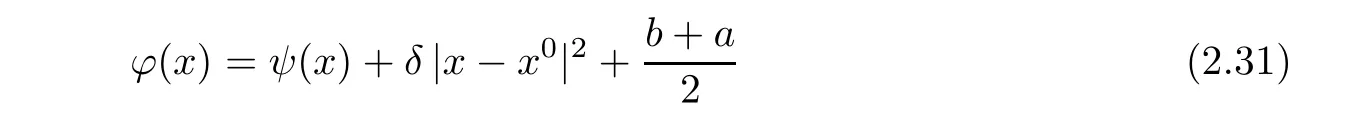
and consider the set

On one hand,x0∈G.Indeed,using(2.31)and b−a>0,we find that
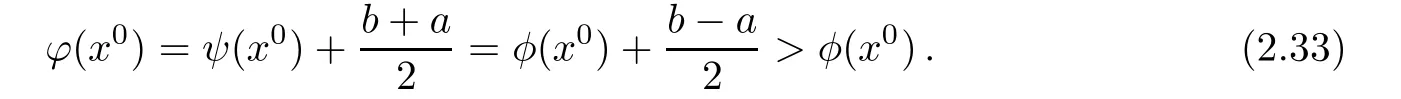
On the other hand,for x ∈ ∂Ω,we have φ(x)− ψ(x)≥ b so that,by(2.31),

Hence,G∩ ∂Ω = ∅and consequently∂G={x∈ Ω:ϕ(x)= φ(x)}.Hence,using Lemma 2.5 and Lemma 2.6,we conclude

which contradicts(2.28).This completes the proof.
2.4 Generalized solutions
The bi-planar Monge-Ampère measure can be used to define the analog of Aleksandrov generalized solutions for the bi-planar Monge-Ampère equation.
Definition 2.8Let Ω ⊂ R3be open and let ν be a Borel measure on Ω.Then,the bi-planar convex function φ ∈ C(Ω)is a generalized solution of the bi-planar Monge-Ampère equation
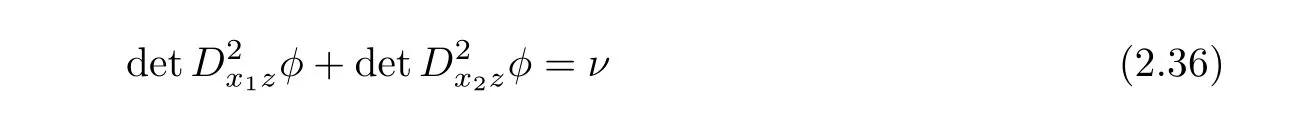
if the bi-planar Monge-Ampère measure associated with φ equals ν.
The following statement is then a direct consequence of Lemma 2.3.
Proposition 2.9Let Ω ⊂ R3be open,and suppose that the Borel measure ν is absolutely continuous with respect to the Lebesgue measure with non-negative density function f ∈ C(Ω).Then,φ is a generalized solution of(2.36)if and only if

Finally,the comparison principle implies the uniqueness of generalized solutions.
Theorem 2.10Let Ω ⊂ R3be open and bounded, ν a Borel measure on Ω,and g ∈C(∂Ω).If φ1and φ2are generalized solutions to the Dirichlet problem

then u1=u2.
3 Non-Existence Results
In this section,we present main results of this article with corresponding examples:there is a domain and boundary data such that no generalized solution to the Dirichlet problem with zero or constant right hand side exist.
3.1 Non-existence of convex generalized solutions
We begin the discussion with a weaker result,namely,there is no generalized solution in the class of convex functions.This construction illustrates in a particularly transparent way how convexity over-constrains the system.We begin with a simple observation.
Lemma 3.1Let A be a symmetric positive semi-definite matrix,written as

Then detS=0 implies detA=0.
ProofBy assumption,the submatrix S must also be symmetric positive semi-definite.Moreover,as S is singular,we can take a nonzero v∈KerS and set wT=(0,vT).Then,wTAw=vTSv=0,so A cannot be strictly positive definite.This implies detA=0.
Lemma 3.1 implies that if problem(2.38)with ν=0 has a convex solution,then the solution also satisfies the classical homogeneous Monge-Ampère equation

From this observation,we conclude the following.
Proposition 3.2There exist a bounded domain Ω and a continuous function g defined on ∂Ω such that problem(2.38)with ν =0 has no solution in the class of convex functions.
ProofLet U ⊂ R2be a bounded domain andThen,Ω is a bounded domain in R3.Let g be a restriction of the functionto the set ∂Ω.Then,φ is a solution of(3.2).This solution is unique[4,9].Now,suppose that φ1is a convex solution of(2.38)with the same boundary data g.By Lemma 3.1,φ1is also a solution of(3.2),that is,.But
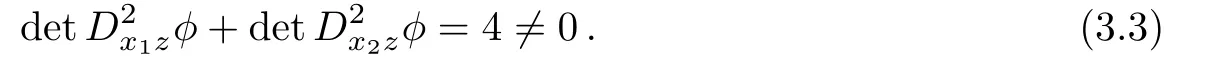
Thus,problem(2.38)with boundary data g does not have a convex solution.
Remark 3.3The existence of generalized solution for the homogeneous Dirichlet problem(3.2)for strictly convex domains is well known,for example,[4,Theorem 1.5.2].Clearly,the difference between convexity and strict convexity of the domain is not an issue here.A similar counter-example can be produced,for example,on the unit ball in R3:Let g be the restriction of the functionto the unit sphere ∂Ω.Then,proceeding as in the proof of Proposition 3.2,problem(2.38)with boundary data g does not have a convex solution.
Remark 3.4Actually,g in the proof of Proposition 3.2 can be written asThen,is the unique concave solution to problem(2.38)and also a concave solution to problem(3.2),unique by the concave analog to Theorem 2.10.
Remark 3.5For boundary dataon the unit sphere Ω,there is neither a concave nor a convex solution to problem(2.38).Indeed,asg(x)can be written as

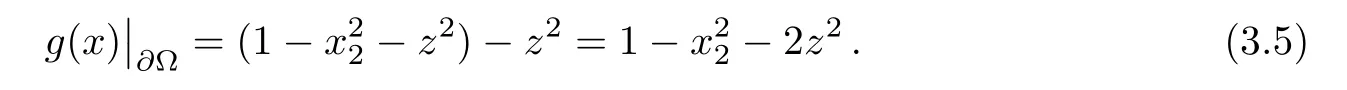
3.2 Non-existence of bi-planar convex generalized solutions
We now re fine the construction to show that relaxing the constraint from convexity to bi-planar convexity does not help:there exists a smooth boundary condition for the Dirichlet problem such that the bi-planar Monge-Ampère equation does not have a generalized solution.
Theorem 3.6Let Ω be the unit ball centered at the origin and λ ∈ [0,8)be fixed.Then,the problem

has no generalized solution in the class of continuous bi-planar convex functions.
ProofSuppose that problem(3.6)has a generalized solutionBi-planar convexity implies that each of the measures µ1and µ2is positive.Asµ1+µ2= λ,we have
in the sense of measure for i=1,2.
Now,consider two classical Monge-Ampère equations.First, fix|x2|<1 and consider

The smooth function

solves(3.8).Furthermore,φ1is convex,therefore it is the unique generalized solution;see,for example,[4,Corollary 1.4.7].Similarly,we fix|x1|<1 and consider the problem

Here,the unique generalized solution is the smooth convex function

We further set
In particular,for x=(0,0,0),we get

Remark 3.7Note that problem(3.6)has a classical solution,

for any λ ≥ 0.When λ ≥ 8,this function is convex,hence bi-planar convex.When 0≤ λ <8,thenis not positive semi-definite so that φ is not bi-planar convex.However,even in this case,problem(3.6)satisfies the ellipticity condition(1.5)for the bi-planar Monge-Ampère equation.
4 Discussion
Our counter-examples show that ellipticity for the bi-planar Monge-Ampère equation is a substantially weaker condition than bi-planar convexity,while bi-planar convexity implies ellipticity.In contrast,for the classical Monge-Ampère equation,ellipticity and convexity coincide,which makes Aleksandrov generalized solutions a useful concept.For the bi-planar equation,there is a“gap”between ellipticity and bi-planar convexity,so that the requirements of convex analysis,necessary to obtain generalized solutions in the sense of Aleksandrov,over-constrain the system.Therefore,a useful solution concept for the bi-planar Monge-Ampère equation requires a different setting,possibly in more traditional function space setting as,for example,in[6,7].This question is left open for future work.
 Acta Mathematica Scientia(English Series)2020年2期
Acta Mathematica Scientia(English Series)2020年2期
- Acta Mathematica Scientia(English Series)的其它文章
- INFINITE SERIES FORMULAE RELATED TO GAUSS AND BAILEY-SUMS∗
- MULTI-BUMP SOLUTIONS FOR NONLINEAR CHOQUARD EQUATION WITH POTENTIAL WELLS AND A GENERAL NONLINEARITY∗
- ASYMPTOTIC BEHAVIOR OF SOLUTION BRANCHES OF NONLOCAL BOUNDARY VALUE PROBLEMS∗
- ASYMPTOTIC DISTRIBUTION IN DIRECTED FINITE WEIGHTED RANDOM GRAPHS WITH AN INCREASING BI-DEGREE SEQUENCE∗
- SOME METRIC AND TOPOLOGICAL PROPERTIES OF NEARLY STRONGLY AND NEARLY VERY CONVEX SPACES∗
- INFINITELY MANY SOLUTIONS WITH PEAKS FOR A FRACTIONAL SYSTEM IN RN∗
