MULTI-BUMP SOLUTIONS FOR NONLINEAR CHOQUARD EQUATION WITH POTENTIAL WELLS AND A GENERAL NONLINEARITY∗
College of Science,Huazhong Agricultural University,Wuhan 430070,China
E-mail:lguo@mails.ccnu.edu.cn;lguo@mail.hzau.edu.cn
Tingxi HU†
School of Mathematics and Statistics,Southwest University,Chongqing 400715,China
E-mail:tingxihu@swu.edu.cn
Abstract In this article,we study the existence and asymptotic behavior of multi-bump solutions for nonlinear Choquard equation with a general nonlinearity
Key words Nonlinear Choquard equation;nonlocal nonlinearities;multi-bump solutions;variational methods
1 Introduction and Main Results
Recently,the following nonlinear Choquard equation



Equation(1.2)was firstly proposed by Pekar on quantum theory of a Polaron in 1954.And then Choquard took advantage of equation(1.2)to describe an electron trapped in a hole.Lieb and Simon[2]also used equation(1.2)as a certain approximation in Hartree-Fock theory for one-component plasma.
We would like to point out that in the last years,many researchers have studied equation(1.2)or a more general case

As far as we know,very few works are concerned with the generalized nonlinear Choquard equation(1.1).In[14],Moroz and Van Schaftingen proved that if V≡1,for each s∈R,and if the function f satisfies


During the past few years,many researchers considered the following Schrödinger equation with potential well

where a(x)and b(x)are continuous and p∈ (2,2∗)if N ≥ 3;p∈ (2,∞)if N=1,2.Under some proper assumptions on a(x)and b(x),they constructed different kinds of solutions which localize near the potential well Ω =int(a−1(0))if λ is large enough;see for examples[16–22].Such kind of bump solutions was also studied for the nonlinear Choquard equation(1.3)with V(x)=λa(x)+b(x).In[23],Lü proved the existence and concentration behavior of singlebump solution to equation(1.3)when λ is large enough.If Ω has k disjoint open componentsΩ1,Ω2,···,Ωk⊂ Ω,Alves,Nóbrega,and Yang[24]showed that the above problem has at least 2k−1 geometrically distinct multi-bump solutions for large value λ.A natural question is that can we establish some results on the existence of multi-bump solutions to equation(1.3)under much weaker assumptions on function f.
In this article,we consider the following nonlinear Choquard equation
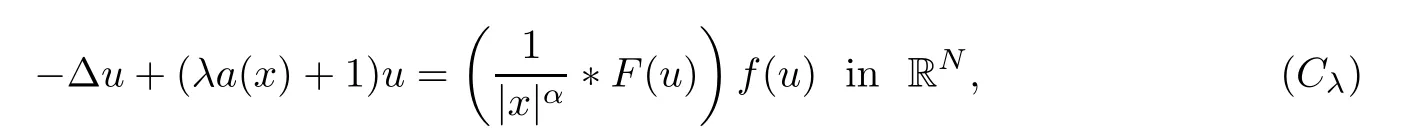
where N≥3 and 0<α (f1)f(s)=o(s)as s→0; (f3)f(s)s>0; (f4)is nondecreasing for|s|>0. Similar to the assumption in[16],the potential a(x)satisfies (A1)a(x)∈C(RN,R)such that a(x)≥0; (A2)There exists a∞>0 such thatµ{x∈RN|a(x) Remark 1.1The condition(f4)implies that H(s):=f(s)s−2F(s)is a nonnegative function and increasing in|s|with Remark 1.2The condition(f3)implies that F(s)>0. To overcome this obstacle,we adapt a new idea introduced by Alves et al.[24]and firstly consider the following limit problem Our result on this aspect can be stated as follows. Theorem 1.1Assume that N≥3,0<α On the basis of the results above,we then construct a solution to equation(Cλ)as λ large and consider the asymptotic shape of the solution as λ → +∞. Theorem 1.2Assume that N≥3,0<α Obviously,Hλembeds into H1(RN)continuously for each λ ≥ 0.We also define the energy functional associated with(Cλ)as This article is organized as follows.In Section 2 and Section 3,we study the limit problem on bounded domain ΩΓwith Γ ={1,···,l}.Using constraint minimization method,we show that the limit problem(C∞,Γ)has a least energy solution with the propertyfor each i∈ Γ.In Section 4,we verify that the functional Jλsatisfies(PS)condition for λ large enough.In Section 5,the behavior of(PS)∞sequence is studied,which plays an important role in proving Theorem 1.2.To obtain the existence of multi-bump solutions,in Sections 6 and 7,we use the deformation flow method introduced in[19],and then complete the proof of Theorem 1.2. In the sequel,we define the usual norm of Lq(RN)(1≤q<∞)and H1(RN),respectively,by and as well as on(1)denotes the quantities tending towards zero as n→∞,oR(1)denotes the small quantities as R is large,and C,Ci,anddenote positive constants which are used to denote various positive constants in different places. The aim of this section is to study the limit problem(C∞,Γ)and find some minimizers of the energy functional associated to equation(C∞,Γ)on a suitable function set.Precisely,we denote by JΓthe energy functional associated with equation(C∞,Γ),that is and let be the Nehari manifold of JΓ.In the following,we consider the minimizing problem where First of all,we must prove that the set MΓis not empty.To begin with,we introduce the following inequality which will be frequently used to study the nonlocal term. Proposition 2.1(Hardy-Littlewood-Sobolev inequality[25]) Let p,r>1 and 0<α Lemma 2.2Suppose that N ≥ 3,0< α ProofAswiththen let variables si≥ 0,i=1,2,···,l and define the function Under assumptions(f3)and(f4),we have F(u)≥ Cu2asLet|(s1,s2,···,sl)|→+∞,we then getand furthermore, for some constant C,which implies that I(s1,s2,···,sl)→ −∞.As I is a continuous function onthen we can prove that there exists a global maximum pointfor I. On the other hand,if I(s1,s2,···,sl)is a strict concave function,thenis the unique global maximum point of I andUsing the semi group property of the Riesz potential(see[25]5.10(3)):and taking it into consideration thatfor,we have from which we deduce that Note that by(f1),one hasas s → 0.Hence,we getfor s>0 sufficiently small,which is a contradiction to the fact thatis the unique global maximum point of I. Before completing the proof of this lemma,we still need to proveIndeed,for any w∈MΓ,we have Lemma 2.3Assume that N ≥ 3,0< α ProofAssume by contradiction that w1=0.On one hand,by(f1)–(f2),we knowthen using Hardy-Littlewood-Sobolev inequality,we get which contradicts the assumptionSimilarly,we can prove thatfor each i∈ Γ. ? By Lemma 2.2,there exists a sequence ofsuch that From(3.1),we know,for any t∈ R satisfying|t|is sufficiently small,that function JΓ(wn+twn,i)achieves its maximum point at t=0.By taking derivative with respect to t at t=0,we have At this point,with a similar argument used in(2.6),we then get where C>0 depends on the upper bound of the norm of{wn}.Hence,we getfor any n∈N and then as a direct consequence of Lemma 2.3,we getfor i∈Γ.Then,by Lemma 2.2,there exist t1,t2,···,tl>0 such that for i,j∈Γ.Furthermore,direct calculation shows that Moreover,we fix r>0 small enough such that(s1,s2,···,sl)∈ Qr:=(1−r,1+r)l⊂ Rl,then there exists some ε0>0 such that In the following part,we fix ε∈ (0,ε0)and δ>0 small enough,such that where By the classical deformation lemma[26],there exists a continuous mapsuch that and By the following lemma,it is easy to prove that w∗is a critical point for JΓ.As the proof of this lemma is similar to the Claim 2.3 in[24],then we omit it here. Lemma 3.1There exists(s1,s2,···,sl)∈ Qrsuch that From Lemma 3.1 and(3.10),we see that there exists(s1,s2,···,sl)∈ Qrsuch that and so, which cannot happen.Thus,we prove that w∗is a critical point of JΓ. In this section,we prove that for a given c ≥ 0 independent of λ,the functional Jλsatisfies the(PS)dcondition for 0 ≤ d Lemma 4.1Letbe a(PS)csequence for Jλ,then{un}is bounded.Furthermore,c≥0. ProofSuppose that{un} ⊂ Hλis a(PS)csequence for Jλ,that isandas n→+∞.Then, In fact,as and f(u)u≥2F(u)≥0,then Therefore,from(4.1)and(4.4),we get which implies{un}is bounded in Hλand c≥0 by taking the limit of n→+∞. Corollary 4.1Let{un}⊂Hλis a(PS)0sequence for Jλ,then un→0 in Hλ. Next,we prove a Brézis-Lieb type Lemma of Jλ. Lemma 4.2Let c≥ 0,λ>0 and{un}be a(PS)csequence for Jλ.Ifin Hλ,then where vn=un− u.Furthermore,{vn}is asequence. ProofIn order to prove this lemma,we only need a Brézis-Lieb type lemma for the nonlocal term By a direct computation,one has Applying the Hardy-Littlewood-Sobolev inequality to the nonlocal terms in(4.9)–(4.11),one has for some C>0. As{un}is bounded in Hλ,then,by(f1)and(f2),there exists a constantdepending on the bound of{un},such that On the other hand, By Hölder inequality,we obtain Thus,from(4.13)–(4.16),taking the limit n→+∞ firstly,then R→+∞,we can obtain Before completing the proof of the lemma,we need to prove On the basis of the result above andwe then prove(4.18). The following lemma shows that the zero energy level of(PS)csequence of Jλis isolated. Lemma 4.3Let{un}be a(PS)csequence for Jλ,then either c=0,or there exists a constant c∗>0 independent of λ,such that c≥ c∗,∀ λ >0. Using the Hardy-Littlewood-Sobolev inequality,Sobolev inequality together with(f1)and(f2)again,we have where positive constant C is independent of λ. Lemma 4.4Let{un}be a(PS)csequence for Jλ.Then,there exists a constant δ0>0 independent of λ,such that ProofAs{un}is a(PS)csequence for Jλ,then Lemma 4.5Let c1>0 independent of λ and{un}be a(PS)csequence for Jλwith c ∈ [0,c1].Given ε >0,there exist Λ = Λ(ε)and R(ε,c1)such that ProofFor R>0,we consider Then, As c1is independent of λ,then by(4.22),we deduce that there exists Λ >0,such that On the other hand,using the Hölder inequality and Sobolev embedding theorem,we have By(A2),we know thatµ(B(R))→0 when R→+∞,and we can choose R large enough such that Combining(4.23)with(4.25),we can obtain As{un}is bounded in Hλ,then it follows by interpolation inequality and(4.26)that we have Thus, Proposition 4.6Fixed c1>0,independent of λ,there exists Λ = Λ(c1)such that for each λ ≥ Λ,then Jλsatisfies the(PS)ccondition for all c∈ [0,c1]. ProofLet{un}be a(PS)csequence of Jλ,where λ >0 is large and will be fixed later on.By Lemma 4.1,{un}is bounded.Then,there exists u∈Hλ,such that,up to subsequence,inin RN,andinfor We claim that d:=c−Jλ(u)=0.Arguing by contradiction,we suppose that d>0.By Lemma 4.3 and Lemma 4.4,we have d≥c∗and and so However,it follows by the compactness embeddingforthen and contradicts to(4.28).Thus,d=0 and{vn}is a(PS)0sequence.Furthermore,by Corollary 4.1,vn→ 0 in Hλ.Then,it is obviously that Jλsatisfies(PS)ccondition for c∈ [0,c1]if λ is big enough. In this section,we will prove that the functional Jλsatisfies(PS)∞condition.First,we introduce the definition on(PS)∞sequence.We say{un} ⊂ H1(RN)is a(PS)∞sequence for a family of functional{Jλ}λ≥1,if there exist d ∈ [0,cΓ]and a sequence{λn} ⊂ [1,+∞)with λn→+∞such thatandas n→ ∞,whereis the dual space of Hλn.We also say(PS)∞sequence{un}satisfies(PS)∞condition,if up to a subsequence,{un}is convergent in H1(RN). Proposition 5.1Assume that N≥3,0<α ProofBy a similar argument used in Lemma 4.1,we know{un}is bounded inhence{un}is bounded in H1(RN).Then,up to a subsequence,there exists u∈H1(RN)such thatin H1(RN)and un(x)→u(x)for a.e.x∈RN,and un→u infor Step 1By computation,we know which implies Furthermore,by Hardy-Littlewood-Sobolev inequality again,we get Then by(5.2)–(5.4),we have Thus,un→u in H1(RN)and(1)holds. As un→u in H1(RN),then Then,we complete the proof of(2). Step 3Direct calculation shows that Then,the proof of(3)is completed. Step 4By Step 1,we knowthen for each i∈ Γ, which yields(4). Step 5Note that By the property(3),(5.6)and the fact thatit is easy to prove that Step 6The functional Jλncan be written in the following way By Step 1 to Step 5,we have Next,we consider the nonlocal terms.As un→u in H1(RN),then On the other hand,as and then A direct calculation shows that By(5.8)–(5.13),we have In this section,without loss of generality,we still consider Γ ={1,···,l}with l ≤ k.Moreover,we denote byan open neighborhood of Ωiwithifand setWe also define which is the energy functional connected with the Choquard equation with Neumann boundary condition Recalling that,similar as the definition on cΓ,NΓ,and MΓin Section 2,we define With a similar arguments in Section 2,we know that there existsand wλ,Γ∈such that Proposition 6.1The following properties hold: (i)0 (ii)cλ,Γ→ cΓas λ → +∞. Proof(i)The proof is trivial,so we omit it. (ii)Let λn→ +∞.For each λn,there existswith Moreover, and By the definition of cΓ,then we have Thus,by conclusion(i)and(6.5),we get,as ni→ +∞. In the following parts,we define bythe least energy solution obtained in Section 3,that is We know that Furthermore,changing variables bythen we obtain By a similar argument explored in Section 3,we know I(s1,s2,···,sl)is strictly concave and∇I(1,···,1)=0.Hence,(1,···,1)is the unique global maximum point of I on[0,+∞)lwith I(1,···,1)=cΓ. Under the assumptions(f1)–(f4),with a direct calculation,we can prove that there exists r>0 small enough and R>0 large enough such that Moreover, Let Γ∗be the class of continuous pathwhich satisfies the following conditions where R>1>r>0 are positive constants obtained in(6.8)and(6.9).Obviously,γ0∈ Γ∗,thenBy Miranda’s theorem,we can easily prove the following lemma. In this section,we will prove the existence of nonnegative solution uλif λ is large enough.Moreover,we prove that the solution uλconverges to a least energy solution of(C∞,Γ)as λ→+∞and then complete the proof of Theorem 1.2. Before the proof,we introduce some notations and define where r is fixed in(6.9)and τ is a positive constant such that for any i∈ Γ, Proposition 7.1For each η >0,there exist Λ∗≥ 1 and δ0independent of λ such that Moreover,u is a solution of Taking limit of n→+∞in(7.6),then we get Next,we give some notations which will be used in the following part.We define where δ was given in(7.2)and We also define the set For the readers’convenience,we divide the proof of this proposition into several steps and prove the conclusion step by step. Step 1Construction of a deformation flow. From Proposition 7.1,there exists Λ∗such that In what follows,we define a continuous functionalwhich satisfies 0≤ Ψ(u)≤ 1,∀u∈Hλand where g is a pseudo-gradient vector field for Jλonand G is well defined.It is easy to observe that Then,by the classical deformation lemma[26],we can prove that there exists a deformation flowdefined by such that and Step 2Estimation on the paths σ(t,γ0(t1,···,tl))and γ0(t1,···,tl). We study the following two paths: (1)Consider the path(t1,···,tl)→ σ(t,γ0(t1,···,tl)),where(t1,···,tl)∈ [r,R]l,t≥ 0. As η ∈ (0,η∗),by the definition of η and η∗before,we have thus, and then By(7.17)and(7.19),then By the choice of δ,it follows thatfor anyIfthen σ(t,γ0(t1,···,tl))=γ0(t1,···,tl).While,ifby the deformation lemma,σ(t,γ0(t1,···,tl))belongs to the closure ofthus we have and Consequently, It is easy to see that and Moreover,(t1,···,tl)=(1,···,1)is the maximum point of Jλ(γ0(t1,···,tl))and In the following,we assume there exists K∗>0 sufficiently large,such that Step 3Prove that for some T>0. In fact,let u=γ0(t1,···,tl),where(t1,···,tl)∈[r,R]l.On one hand,ifby(7.15),we can easily get Case 1∀t∈[0,T], Case 2∃t0∈[0,T]satisfies For Case 1,by the definition of Ψ,we haveBy(7.12)–(7.13),for t∈[0,T].Hence,by(7.15),we have which yields(7.23). For Case 2,we divide the argument into 3 situations: (1)There exists T2∈[0,T]such that.By choosing T1=0,asand(7.9),it follows that (2)There exists T2∈[0,T]such that.By choosing T1=0,asand(7.9),we get Then, Then,using the mean value theorem,we know.Notice that On the basis of(7.27)–(7.30),we then prove that(7.23)is true. On the other hand,we obtain which implies that which is absurd.? Proof of Theorem 1.2By Proposition 7.2,we prove that there exists a sequence of{uλn}with λn→ +∞ satisfying the following properties: Thus,by the conclusion of Proposition 5.1,we obtainstrongly in H1(RN),where u ∈ H1(RN)satisfiesand u=0 outside ΩΓ,i∈ Γ.This finishes the proof of Theorem 1.2. ? AcknowledgementsThe authors would like to thank Prof.Shuangjie Peng for stimulating discussions and helpful suggestions on this article.The first author thanks Prof.Minbo Yang very much for some useful discussions.


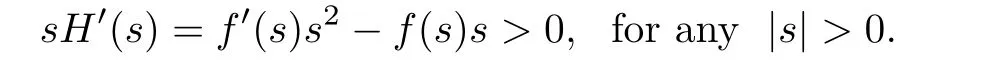









2 The Limit Problem(C∞,Γ)



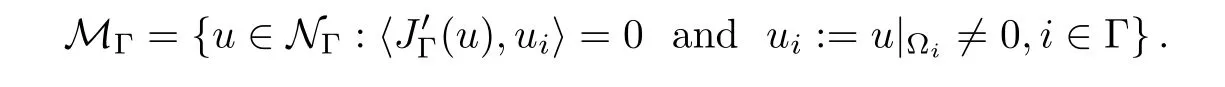
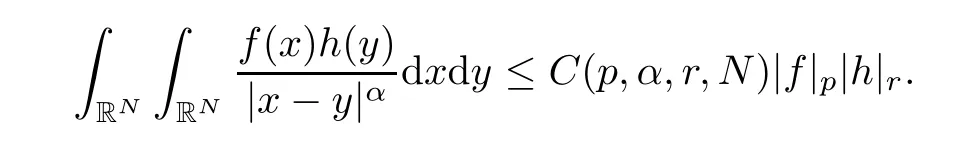






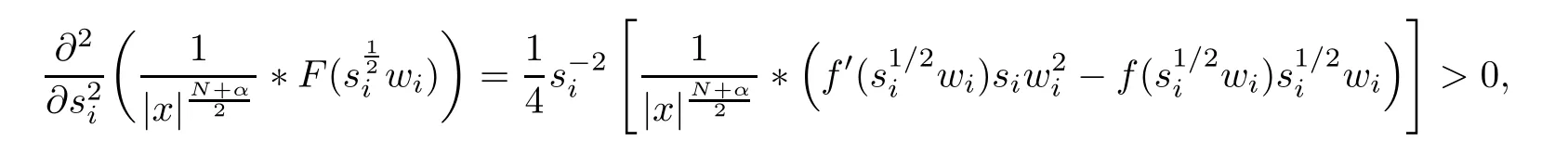
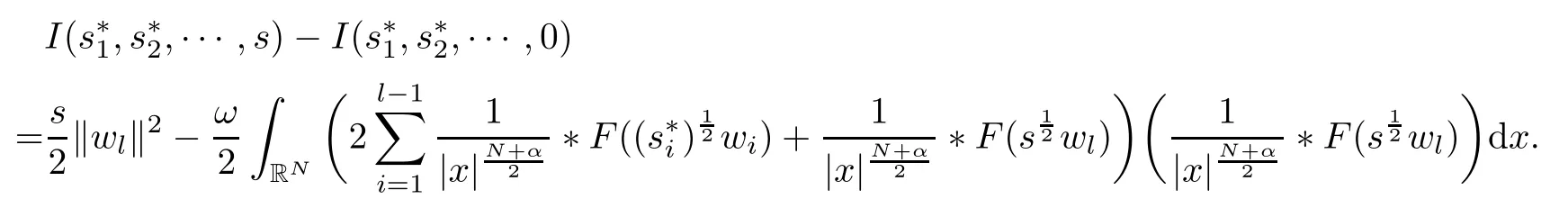
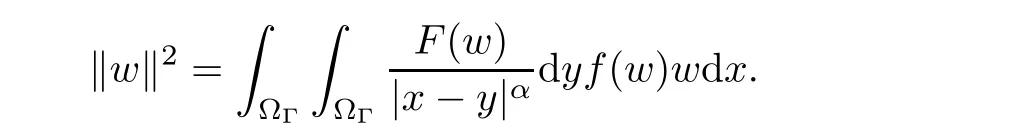

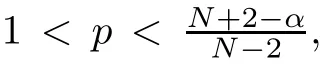
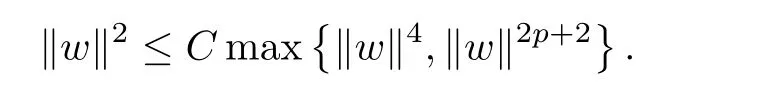

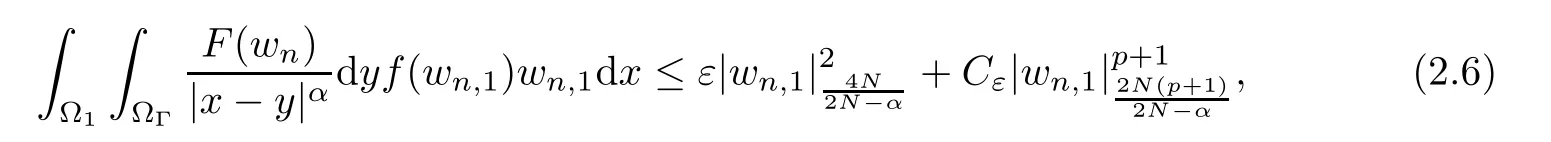



3 Proof of Theorem 1.1



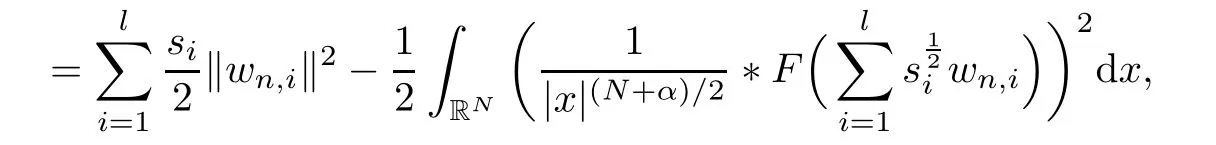

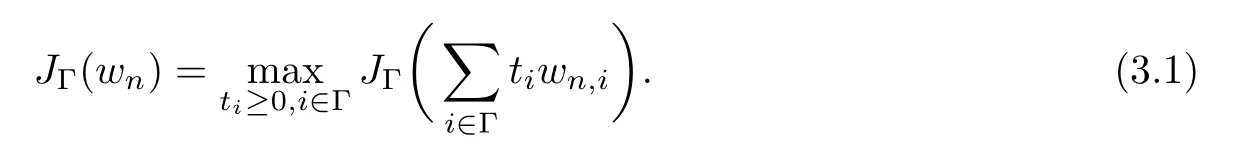


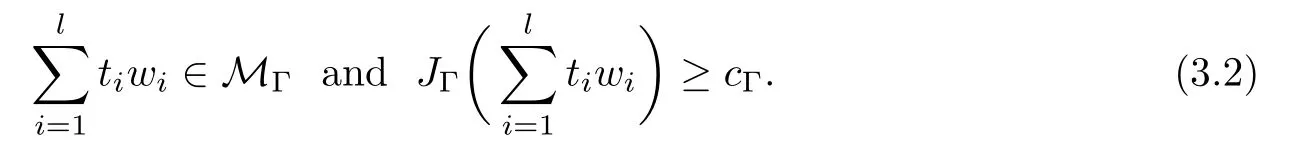







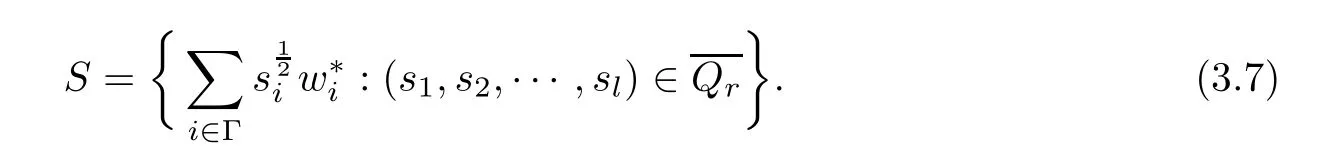


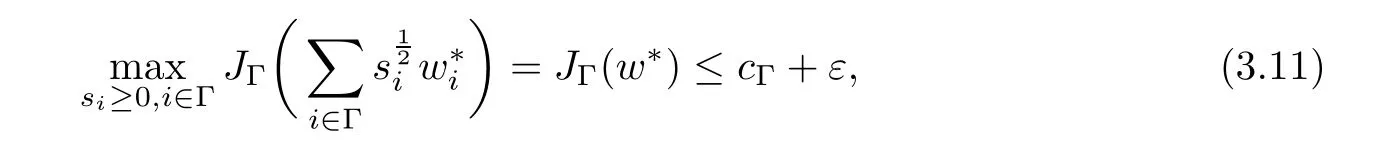
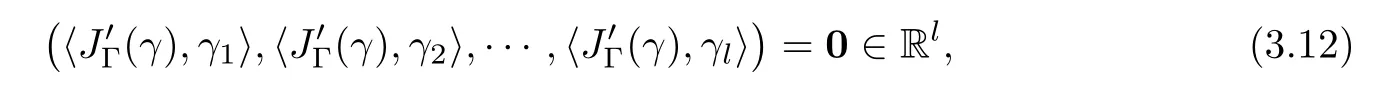
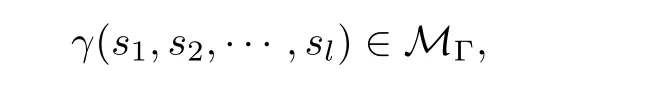

4 The(PS)cCondition for Jλ



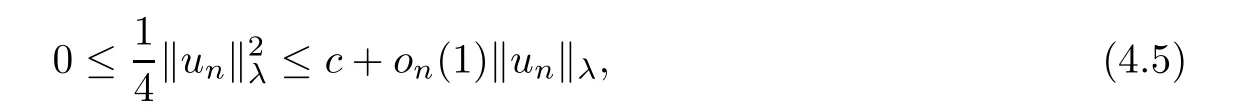





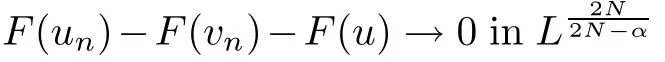












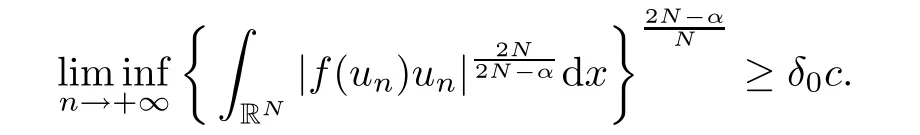








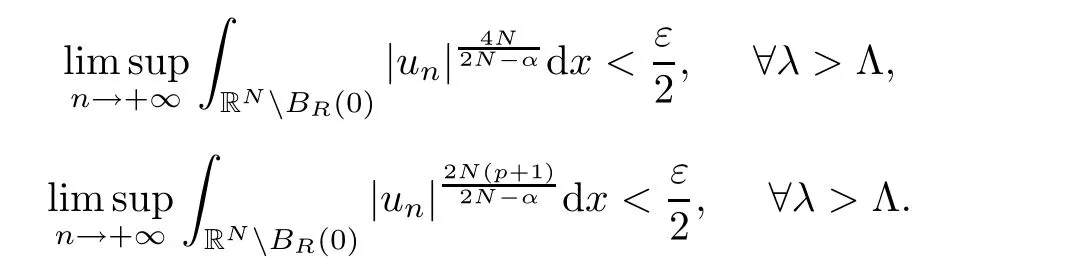





5 The(PS)∞Condition


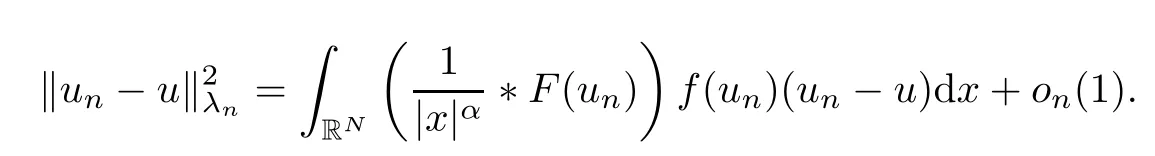








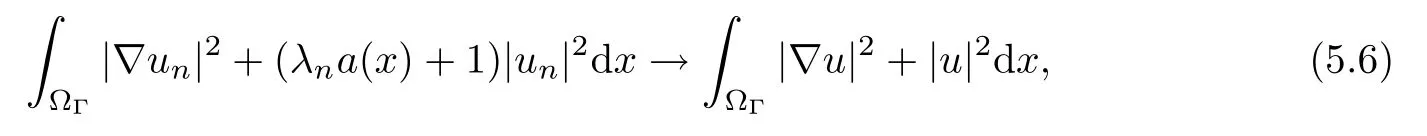
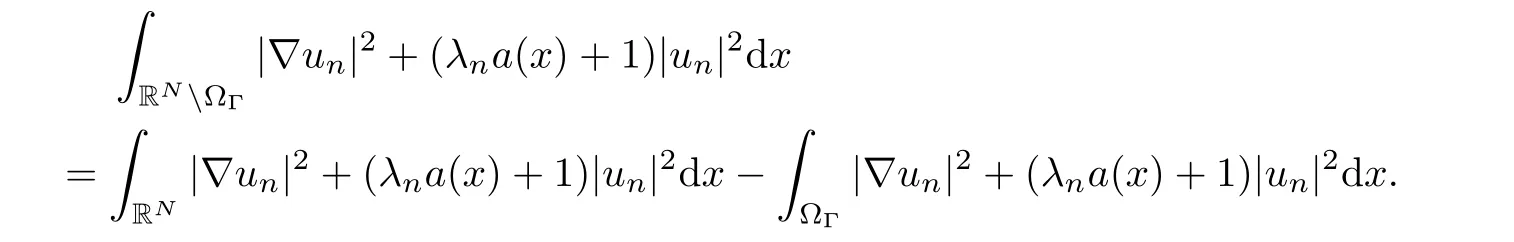




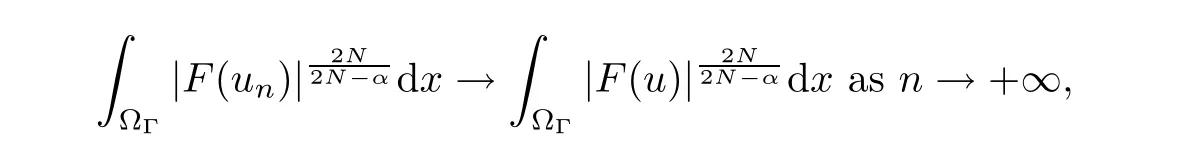
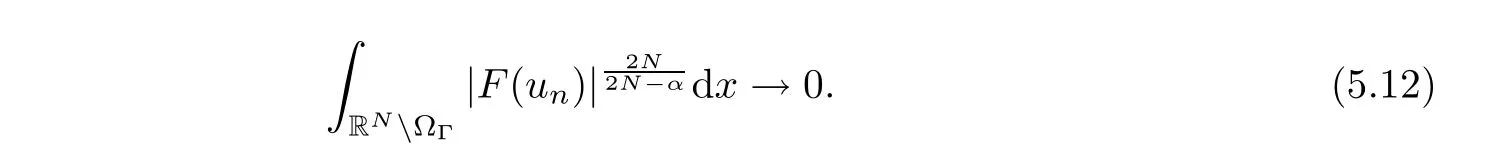


6 Further Propositions for cΓ
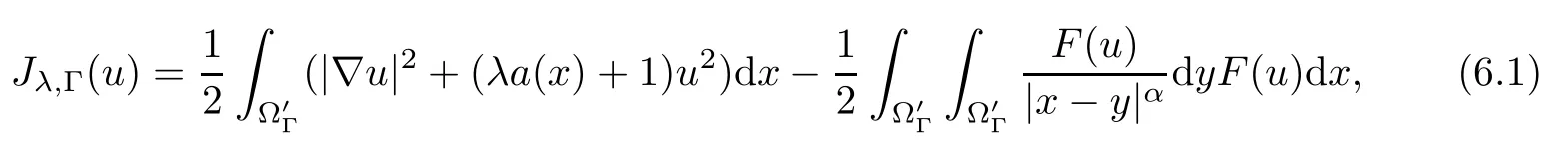
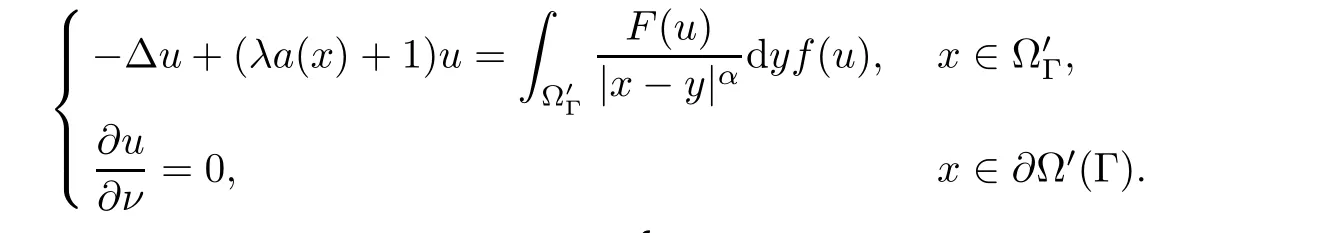
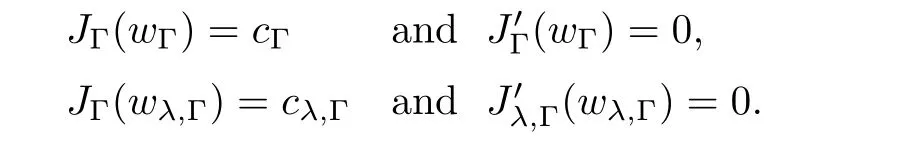






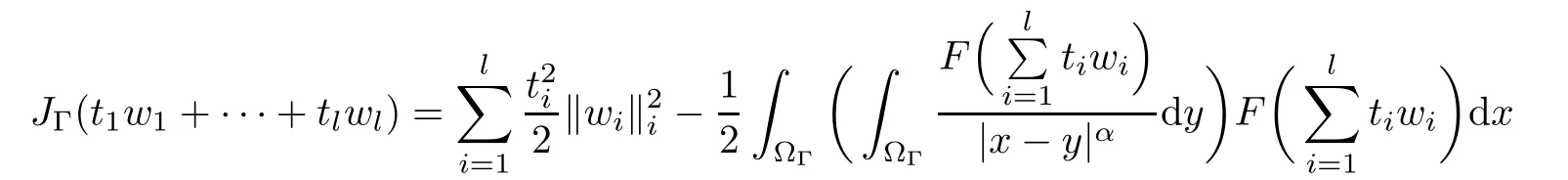


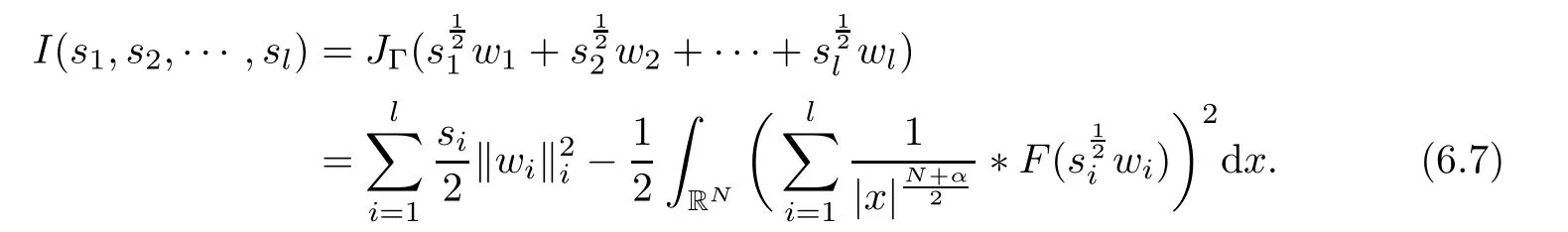
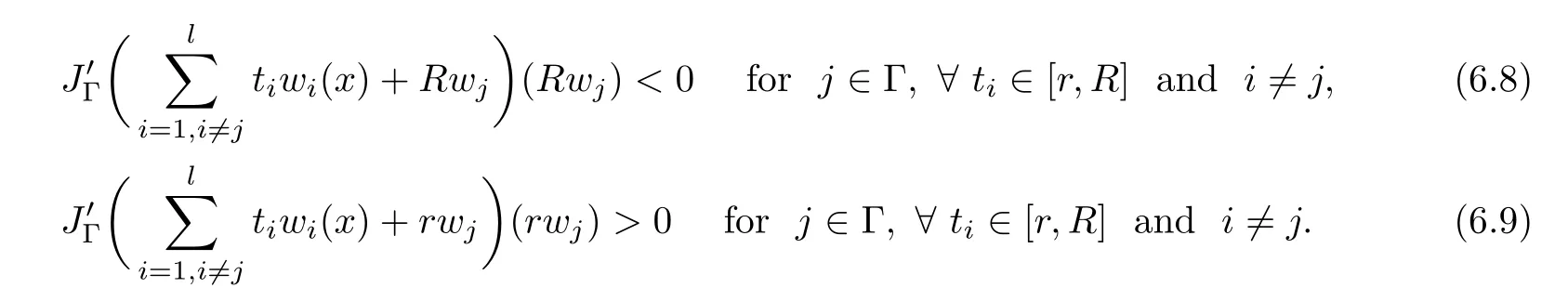




7 Proof of Theorem 1.2
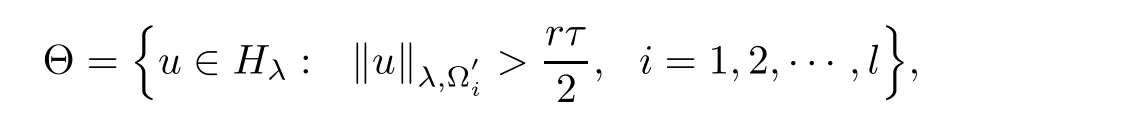






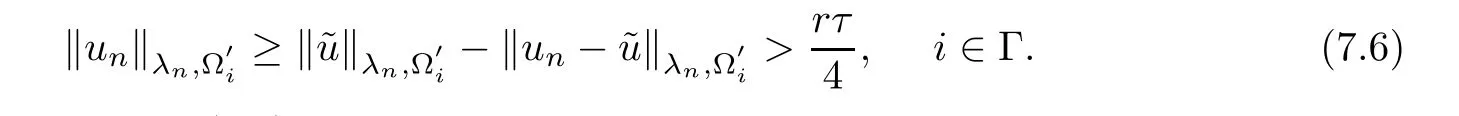



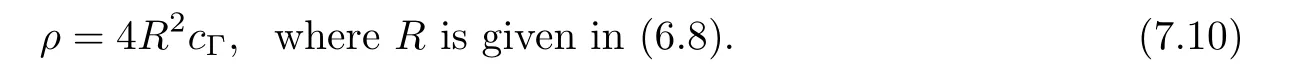
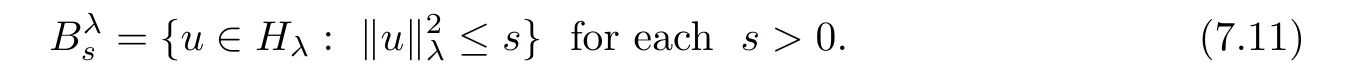

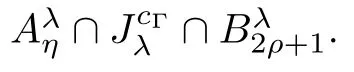


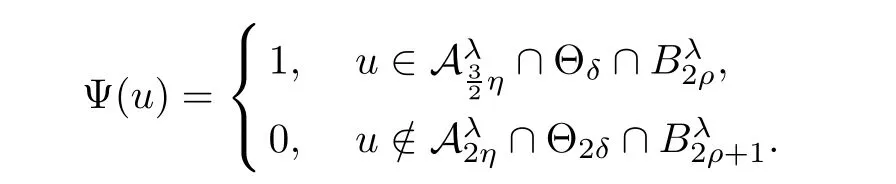




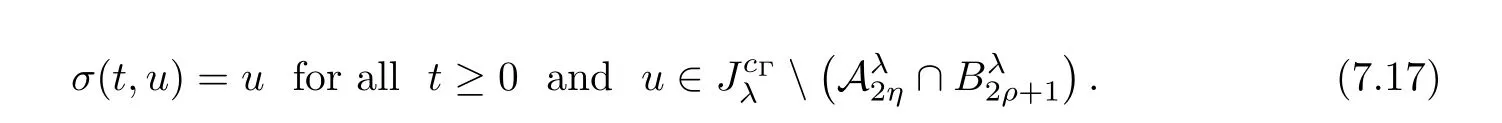



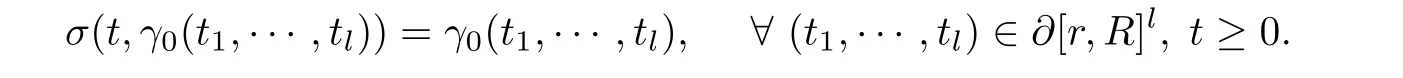



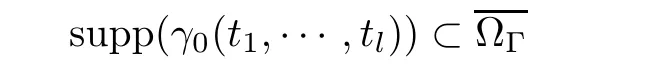


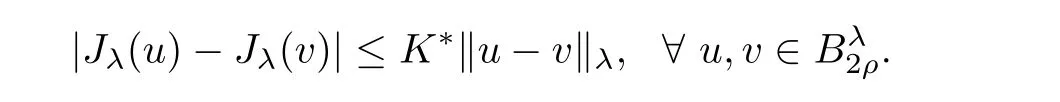

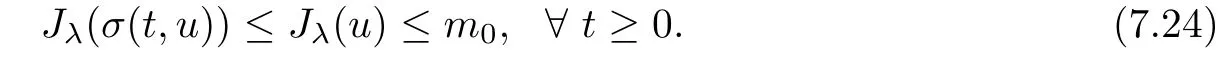

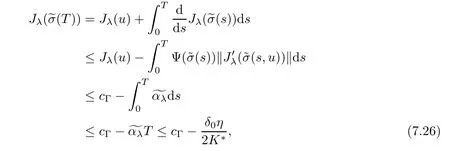







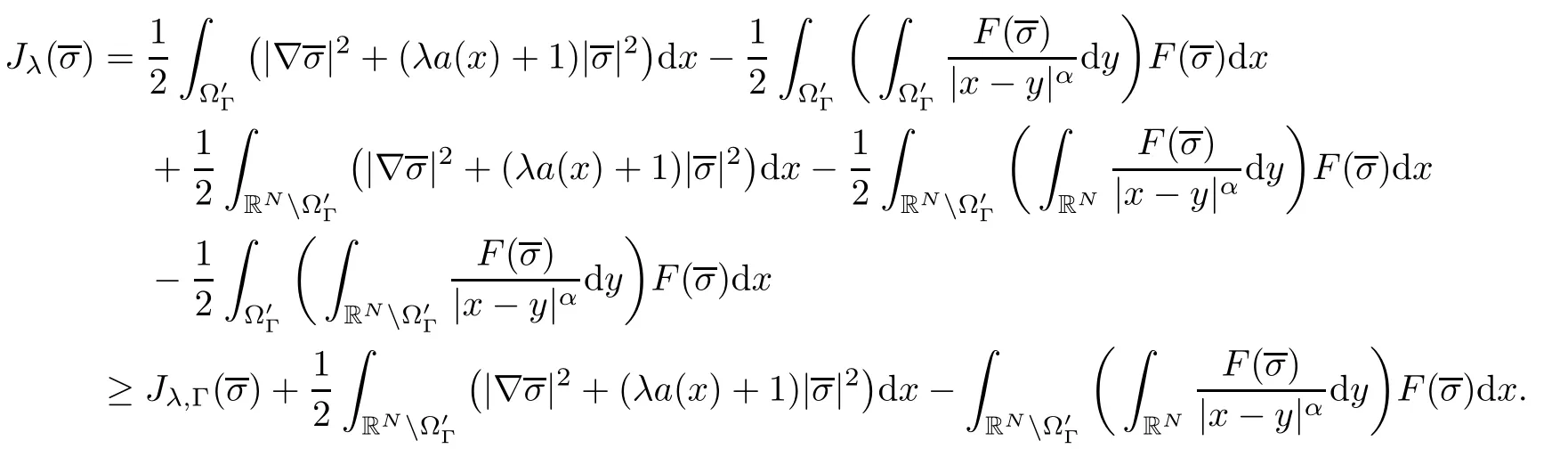



 Acta Mathematica Scientia(English Series)2020年2期
Acta Mathematica Scientia(English Series)2020年2期
