SOME METRIC AND TOPOLOGICAL PROPERTIES OF NEARLY STRONGLY AND NEARLY VERY CONVEX SPACES∗

School of Mathematics,Physics and Statistics,Shanghai University of Engineering Science,Shanghai 201620,China

E-mail:zhz@sues.edu.cn

Vicente MONTESINOS†

Instituto deMatemática Pura y Aplicada,Universitat Politècnica deValència,C/Vera,s/n,46022 Valencia,Spain

E-mail:vmontesinos@mat.upv.es

Chunyan LIU

School of Mathematics,Physics and Statistics,Shanghai University of Engineering Science,Shanghai 201620,China

E-mail:chyliu001@yahoo.com.cn

Abstract We obtain characterizations of nearly strong convexity and nearly very convexity by using the dual concept of S and WS points,related to the so-called Rolewicz’s property(α).We give a characterization of those points in terms of continuity properties of the identity mapping.The connection between these two geometric properties is established,and finally an application to approximative compactness is given.

Key words Banach spaces;nearly strongly convex spaces;nearly very convex spaces;Kadec property;Radon-Riesz property;approximative compactness

1 Introduction and Preliminaries

for all x∗∈ SX∗,where α stands for the Kuratowski index of non-compactness(that is,α(S)is the infimum of numbers r>0 such that S can be covered by a finite number of subsets having diameter less that r)andis the ε-slice of BXdefined by x∗.Property(α)was introduced by S.Rolewicz.The second named author proved that it is equivalent to X having the so-called drop property,which in turn is equivalent to X being reflexive and having the Radon-Riesz property(H)[12](a Banach space X has the Radon-Riesz property(H)whenever the w-convergence of a sequence in SXto a point x in SXis equivalent to the-convergence to x).

In order to avoid the restriction of reflexivity —itself a consequence of James’compactness theorem—in the previous concept,J.H.Wang and the first named author introduced in[13]the so-called nearly strong convexity,where the(α)property is checked only on the set NA(X)of norm-attaining functionals.Precisely,if D denotes the duality mapping,that is,for x ∈SX,the definition reads:

Definition 1.1(Wang,Zhang) Letbe a Banach space,and let x0∈ SX.The normis said to be strongly convex at x0(nearly strongly convex at x0)if givenand a sequence{xn}in BXsuch thatthen(respectively,the set{xn:n∈N}is relatively compact).If the set{xn:n∈N}is just weakly relatively compact,the norm is said to be nearly very convex at x0.The norm is said to be strongly convex if it is strongly convex at every point of SX.The same applies to the nearly strong convexity and nearly very convexity concepts.

That the concept of nearly strong convexity can be written in terms of the property(α)is stated in Proposition 2.8 below.A trivial observation is that we may replace BXby SXin the previous definition.

We follow the notation as in standard texts(see,for example,[5]).For example,if X is a Banach space and x ∈ X,then B(x,ε)denotes the closed ball centered at x and having radius ε>0.The action of an element x∗∈ X∗on an element x∈ X will be denoted by x∗(x)or,alternatively,We shall consider X canonically embedded in its bidual X∗∗.The weak topology on X will be denoted by w(X,X∗)or just w if there is no risk of misunderstanding.The same applies to the weak∗topology on X∗(denoted w(X∗,X)or just,simply,w∗).

Remark 1.2To place the concepts introduced in Definition 1.1 in a proper context,and to see a few connections with some standard geometrical properties of Banach spaces,notice the following almost trivial implications.(Below,LUR is the usual acronym for locally uniformly rotund:The normof a Banach space X is said to be locally uniformly rotund if given a sequence{xn}in X such that kxnk→1 andthenif the convergence of{xn}to x0is in the weak topology,the norm is said to be wLUR.)Then,we have LUR⇒strongly convex⇒nearly strongly convex⇒nearly very convex,and these four concepts are different(see[14,Examples 2.5,2.6,and 2.7])(for examples,outside the context of reflexive spaces—all of them nearly very smooth— consider[3,Theorem 1],where it is proved that every infinite-dimensional Banach space with separable dual admits an equivalent wLUR norm which is not LUR:It is obvious that every wLUR space is nearly very convex;this wLUR equivalent norm cannot be nearly strongly convex,because this last property implies property(H)that,together with wLUR,implies LUR,seeing below).The concepts nearly strongly convex and nearly very convex are discussed,for example,in[1,6,8,14–17],and they are related to questions of approximation in Banach spaces.We may mention,for example,a characterization of nearly strict convexity in terms of the preduality mapping:

(i)[16]X is nearly strongly convex(respectively,nearly very convex)the predual mapping D−1is(respectively,upper semi-continuous onwith norm-compact images(respectively,weak-compact images),and how in nearly strongly convex Banach spaces proximinality and approximative compactness agree:

(ii)[15]X is nearly strongly convexevery proximinal closed convex subset in X is approximatively compact(and conversely).

Remark 1.3Observe that it is equivalent to say thatis nearly strongly convex(nearly very convex)at x0that for everyevery sequence{xn}in BXsuch thathas a-convergent(respectively,w-convergent)subsequence.The statement for the norm topology is a simple consequence of the-compactness(and for the weak topology,of the Eberlein–Šmulyan theorem).

Remark 1.4Observe that the concepts introduced in Definition 1.1 are metric in nature.Indeed,and as an example,ifis nearly very convex at some x0∈ SX,then everydefines a w-compact faceby the Eberlein–Šmulyan theorem.Let us consider the space c0endowed with the supremum normFor n ∈ N,letbe the n-th vector of the canonical basis of c0(respectively,ofThen,defines a face of Bc0that is homeomorphic tohence not w-compact,sois not nearly very convex at en.However,c0—as every separable Banach space— has an equivalent LUR normby a result of M.I.Kadec,and,as it was mentioned in Remark 1.2,is then nearly very convex.

The following lemma has a simple proof.We provide it for the sake of completeness.

Lemma 1.5Let{Sn}be a decreasing sequence of subsets of a complete metric space(M,d).Then,the following statements are equivalent:

(i) α(Sn)→0;

(ii)If xn∈Sn,n∈N,the sequence{xn}has a convergent subsequence;

(iii)If xn∈Sn,n∈N,the set{xn:n∈N}is relatively compact.

Proof(i)⇒(ii).If S:={xn:n∈ N}is finite,we are done.Otherwise, find a finite covering of S1by sets of diameter less than α(S1)+1.One of them must contain an infinite subsequenceof{xn}.This subsequence but its first element is in S2.The same argument gives a subsequenceofin a set of diameter less thanContinue in this way.A diagonal procedure gives a Cauchy subsequence of{xn},and we are done.

(ii)⇒(iii).The statement(ii)implies easily that the set S:={xn:n∈ N}is relatively sequentially compact,and so relative compact.

Lemma 1.6 below is a simple but useful result.It appeared already in a restricted form in[9]and more precisely in[16],where the proof is provided.Given n ∈ N,put In:={1,2,···,n}.

Lemma 1.6Given a non-empty subset A of a Banach space X,n∈N,a subset{fi:i∈In}of X∗,and a set of real numbers{αi:i∈ In},we have

and the second inclusion is an equality if A is convex and the intermediate set in(1.1)is non-empty.

Remark 1.7(i)A straightforward consequence of Lemma 1.6 is that,if f∈SX∗and 0<ε<1,

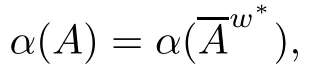
2 Main Results

The following concepts are introduced for dualizing the nearly strong(respectively,very)convexity.

Definition 2.1Let X be a Banach space.Let x0∈SX.We say that x0is an S-point(a WS-point)if given a sequencein BX∗ such thatthen the setis-(respectively,w-)relatively compact.

Remark 2.2Observe that,according to Lemma 1.5 above,it is the same to say that x0is an S-point that x0gives property(α)on BX∗,that is,that α(S(x0,1/n)) → 0 as n → ∞.An easy consequence of Lemmas 1.5 and 1.6 is thatgives property(α)on BX∗∗,if and only if it gives property(α)on BX,that is,ifas n → ∞.An observation similar to Remark 1.3 is that x0is an S-(WS-)point,if and only if any sequencein BX∗ such thathas a(respectively,w-)convergent subsequence.

The connection between S-(WS-)points and points of continuity is given by the following result.In a sense,it is somehow surprising,because a sequential continuity condition turns out to be equivalent to a continuity condition—even in absence of metrizability—.This is true for the norm and for the weak topology as well.Recall that if A is a subset of the dual X∗of a Banach space X,a point x∗∈ A is said to be a(respectively,a w∗-w-)point of continuity of A if x∗is a point of continuity of the identity map from(A,w∗)to(respectively,from(A,w∗)to(A,w)).

Proposition 2.3Letbe a Banach space,and let x∈SX.Then,the followings are equivalent:

(i)x is an S-(respectively,WS-)point;

(ii)Every x∗∈ D(x)is a(respectively w∗-w-)point of continuity of BX∗.

ProofFirst,we shall prove the case of the S property and thecontinuity.

(i)⇒(ii).Assume that x∈ SXis an S-point.Note that,trivially,x∗(x)=1}is a-compact set.FixLetbe a net in BX∗ that w∗-converges to x∗.Let us choose an arbitrary subnet ofwhich,in order to simplify the notation,will be re-written asIn particular,Given n ∈ N,we can find in∈ I such thatfor all i≥ in.Without loss of generality,we may assume that the sequenceis increasing.We have now two possibilities:

a)There exists i0∈I such that in≤i0for all n∈N.This shows,in particular,thatfor all i ≥ i0.As D(x)is-compact,we conclude thathas a-convergent subnet.

b)Assume now the opposite:For all i∈I,there exists n∈N such that i

(ii)⇒(i).Assume now that every x∗∈ D(x)is a w∗--continuity point of BX∗.Letbe a sequence in BX∗ such thatWe shall show thatis-relatively compact.It is enough to check that every infinite subset A ofhas a-cluster point.The set A is w∗-relatively compact,hence it has a w∗-cluster pointObviously,,henceis a w∗--point of continuity.This implies thatis a-cluster point of A.

The case of an WS-point and the w∗-w continuity is similar.

Corollary 2.4Letbe a Banach space.Let x∈ SX.Then,the two following statements are equivalent:

(i)x is a WS-point.

Compare the characterization in Corollary 2.4 with the one in the following Proposition from[16].In a sense,they are dual to each other.

Proposition 2.7 below is a local version of the previous proposition.In order to prove it,we need the following statement that collects several results in[16]:

Theorem 2.6Let(X,be a Banach space.LetandThen,each of the following statements is equivalent to the fact that D−1is-w-usco at

(iii)[16,Theorem 3.6]For every netsuch that,there exists a subnetthat w-converges.

Proposition 2.7Letbe a Banach space.Let x0∈ SX.Then,is nearly very convex at x0,if and only iffor all

ProofAssume thatis nearly very convex at x0,and letIf{xn}is a sequence inby definition,the set{xn:n ∈ N}is w-relatively compact.It follows then,by the Eberlein–Šmulyan theorem,that the setis w-compact.Assume now that there exists a w-neighborhood N of 0(that can be taken to be w-open)such thatdoes not contain any nonempty slice of BXdefined by.Thus,there exists a sequence{xn}in BXsuch thatandfor all n ∈ N.Again by definition,the setis w-relatively compact,hence there exists a w-cluster point x∈BX.Note thatand that,a contradiction.This shows,because of the equivalencein Theorem 2.6,that

We include down a simple proof of the necessary condition in Proposition 2.7 in a particular case,based just on the very definition of near very convexity,in order to have a taste of the argument behind the general proof above.

Proof(of the necessary condition in Proposition 2.7 for separable spaces that do not contain an isomorphic copy of ℓ1) Assume thatis nearly very convex at x0,and letGiventhere exists,by the Odell–Rosenthal theorem(see,for example,[2,page 215]),a sequence{xn}in BXthat w∗-converges toAswe know that{xn:n∈N}is w-relatively compact in X.It follows that(that is,On the other hand(and note that this implication holds without any restriction on the space),iflet{xn}be a sequence in BXsuch thatLetbe a w∗-cluster point of.We haveandis w-relatively compact.

Proposition 2.8 below is somehow the “predual” version of Theorem 3.3 in[16],and collects some information that was given above.

Proposition 2.8Letbe a Banach space.Let x0∈ SX.Then,the followings are equivalent:

(i)k·k is nearly strongly convex at x0;

Proofis just the equivalence(i)(iii)in Lemma 1.5 applied to the sequencewhereis any decreasing sequence of positive numbers.

It is precisely the Kadec property—or its sequential version,the Radon-Riesz property(H),defined above—what makes the difference between the nearly strong and very convexity,as the next result shows.As we mentioned above,neither the Kadec property nor the(H)property can be removed from the statement.Note in passing that the two properties,the Kadec property and property(H),are in general different,and that they coincide if the Banach space has no isomorphic copy of ℓ1(for separable spaces this is a result of Troyanski;in fact,it holds for arbitrary Banach spaces).

Proposition 2.9Let X be a Banach space.Then,the following three conditions are equivalent:

(i)X is nearly strongly convex;

(ii)X is nearly very convex and any x ∈ SXis a point of-continuity of BX∗∗;

(iii)X is nearly very convex and has the Kadec property;

(iv)X is nearly very convex and has property(H).

Proof(i)(ii)(iii)follows from the previous observation,and(iii)(iv)is obvious.(iv)(i)follows easily from the definition and Remark 1.3.

Remark 2.10In[15](respectively,[16]),it was proved that a Banach space X is nearly strongly convex(respectively,nearly very convex),if and only if the predual mapping D−1is(respectively,upper semi-continuous on S(X∗)∩NA(X)with-compact images(respectively,w-compact images).

Remark 2.11Note that Proposition 2.9 shows that(v)in Proposition 2.8 can not be substituted by checking-continuity with respect to BXat points in(⊂ X)instead of-continuity with respect to BX∗∗ at points inIn fact,the former is just the Kadec property of the norm,something that clearly does not imply nearly strong convexity.

Remark 2.121.Note that(iv)⇔(v)in Proposition 2.8 holds when “S-point” in(iv)is replaced by “WS-point”,andcontinuity in(v)by w∗-w-continuity(this is just Proposition 2.3).

2.In view of Proposition 2.8 and item(2.12)in this remark,it is natural to conjecture that(i)⇔(iv)holds whenever “S-point”and “nearly strong convexity” are replaced by “WS-point”and “nearly very convexity”,respectively.This fails in general.For the right equivalence,see Proposition 2.13;for an example of a nearly very convex space with a point x0∈SXthat is not a point of w∗-w-continuity of BX∗∗,see Remark 2.14.

The following result is the right counterpart of Proposition 2.8 for nearly very convexity(see also item(2.12)in Remark 2.12 above).In the proof,we shall need the local version of Proposition 2.5 above,given as Proposition 2.7.

Proposition 2.13Letbe a Banach space.Let x0∈ SX.Then,the followings are equivalent:

Proof(ii)⇒(i).Assume that(ii)holds.By definition,given a sequencein BX∗∗such that,the setis w-relatively compact in X∗∗.In particular,this happens for any sequence{xn}in BXsuch that hxn,x∗0i → 1,so{xn:n ∈ N}is wrelatively compact in X∗∗.Thus,is w-compact in X∗∗.Asby Mazur’s theorem,then{xn:n ∈ N}is w-relatively compact in X.This shows thatis nearly very convex at x0.Proposition 2.3 above shows that given,every pointis of w∗-w-continuity in BX∗∗.In particular,this happens for every

(i)⇒(ii)Assume that(i)holds.Proposition 2.7 shows that for everywe havebe a sequence in BX∗∗such that.Letbe any w∗-cluster point ofObviously,Thus,(⊂X).Becauseis a point of w∗-w-continuity in BX∗∗,then the set:n∈N}is,in fact,w-relatively compact in BX∗∗.This proves thatis a WS-point.

Remark 2.14We provide an example to show that the condition on w∗-w-continuity in item(i)of Proposition 2.13 can not be dropped to get(ii)there.In[11],an example of a(R),not LUR normon c0was given.Later on,it was proved in[3]thatis,in fact,wLUR(henceis nearly very convex).The normis defined as

Let us define now a particular vector inThe sequence,wheredenotes the n-th canonical vector basis of ℓ1,is clearly bounded,w∗-null,and not w-null(consider the vector(1,1,···)in ℓ∞),so it has a-cluster pointLet us compute now the action offor each n∈N.Fixing n∈N,the sequenceis eventually 1,sofor all n∈N.However,the sequenceis eventually 0,soIt follows thatinis w∗-convergent to,but notconvergent.

3 Some Applications to Optimization

The rest of this article deals with some optimization results.Let us collect in the next two definitions the relevant concepts related to approximation.If X is a Banach space,C is a nonempty subset of X,and x∈X,then d(x,C)denotes the distance from x to C.

Definition 3.1([4]) A subset C of a Banach space X is said to be proximinal if PC(x)=for every x∈X.

Definition 3.2([10,19]) A nonempty subset C of a Banach space X is said to be approximatively compact if for anyand any x ∈ X satisfyingthere exists a subsequence ofconverging to an element in C.X is called approximatively compact if every nonempty closed convex subset of X is approximatively compact.

The following results relates the concepts of approximate compactness and nearly strong convexity.

Theorem 3.3([1,6,17]) Let X be a Banach space.Then,the followings are equivalent:

(i)X is nearly strongly convex;

(ii)Every proximinal closed convex subset in X is approximatively compact;

(iii)Every proximinal closed subspace in X is approximatively compact;

(iv)Every proximinal hyperplane in X is approximatively compact.

In[10]it was proved that the equivalence between(i)and(ii)in Theorem 3.4 below,that is the reflexive version of Theorem 3.3.Note that the class of spaces verifying Theorem 3.4 coincides with the class of spaces having the drop property,as it has been mentioned above.

Theorem 3.4Let X be a Banach space.Then,the followings are equivalent:

(i)X is approximatively compact;

(ii)X is reflexive and has the property(H);

(iii)X is reflexive and has the Kadec property;

(iv)X is reflexive and nearly strongly convex.

ProofAs we mentioned above,the equivalence(i)⇔(ii)is in[10].That(ii)implies(iii)follows from the trivial fact that every reflexive space is nearly very convex and by Proposition 2.9,or alternatively from the fact that no reflexive space contains an isomorphic copy of ℓ1and then by using the result of properties(H)and Kadec mentioned immediately before Proposition 2.9.(iii)⇒(iv)is again in Proposition 2.9.In a reflexive space,obviously every nonempty closed convex subset of X is proximinal;then(iv)⇒(i)follows from Theorem 3.3.

AcknowledgementsThe second named author wants to thank the School of Mathematics,Physics and Statistics,Shanghai University of Engineering Science,for its hospitality and the wonderful working conditions provided.