L0-CONVEX COMPACTNESS AND RANDOM NORMAL STRUCTURE IN L0(F,B)∗
Tiexin GUO Erxin ZHANGYachao WANG
School of Mathematics and Statistics,Central South University,Changsha 410083,China
E-mail:tiexinguo@csu.edu.cn;zhangerxin6666@163.com;wychao@csu.edu.cn
George YUAN
Centre for Financial Engineering,Soochow University,Suzhou 215006,China
E-mail:georgeyuan@yahoo.com
Abstract Letbe a Banach space,(Ω,F,P)a probability space,and L0(F,B)the set of equivalence classes of strong random elements(or strongly measurable functions)from(Ω,F,P)toIt is well known that L0(F,B)becomes a complete random normed module,which has played an important role in the process of applications of random normed modules to the theory of Lebesgue-Bochner function spaces and random operator theory.Let V be a closed convex subset of B and L0(F,V)the set of equivalence classes of strong random elements from(Ω,F,P)to V.The central purpose of this article is to prove the following two results:(1)L0(F,V)is L0-convexly compact if and only if V is weakly compact;(2)L0(F,V)has random normal structure if V is weakly compact and has normal structure.As an application,a general random fixed point theorem for a strong random nonexpansive operator is given,which generalizes and improves several well known results.We hope that our new method,namely skillfully combining measurable selection theorems,the theory of random normed modules,and Banach space techniques,can be applied in the other related aspects.
Key words Complete random normed modules; fixed point theorem;L0-convex compactness;random normal structure;random nonexpansive operators
1 Introduction
Random normed modules(brie fly,RN modules)are a random generalization of ordinary normed spaces.The theory of RN modules has undergone a systematic and deep development[8–19]and has also been applied to the study of conditional risk measures[21–25]and backward stochastic equations[20].Motivated by financial applications,we recently presented the notion of L0-convex compactness in[21]and further the notion of random normal structure for an L0-convex subset of an RN module in[20];in particular we proved in[20](see also Section 2 of this article for details)the Browder-Kirk’s fixed point theorem in a complete RN module,which is a random generalization of the famous Browder-Kirk’s fixed point theorem in a Banach space[4,6,7,31,32].The generalized Browder-Kirk’s fixed point theorem was applied to the study of backward stochastic equations and backward stochastic differential equations of nonexpansive type in[20].In this article,we find that the fixed point theorem can be further used to study Bharucha–Reid’s problem,which we introduce in the following statement of backgrounds of random fixed point theory.Letbe a Banach space,(Ω,F,P)a probability space,V⊂B a closed convex subset,and L0(F,B)(L0(F,V))the set of equivalence classes of B-valued(correspondingly,V-valued)strong F-random elements defined on Ω,then L0(F,B)becomes an RN module in a natural fashion and L0(F,V)a closed L0-convex subset of L0(F,B)(see Section 2 of this article).In the process of applying the generalized Browder-Kirk’s fixed point theorem to Bharucha-Reid’s problem,it is very key to solve the following two problems:
(1)When V is weakly compact,is L0(F,V)L0-convexly compact?
(2)When V is a weakly compact convex subset with normal structure,does L0(F,V)have random normal structure?
Random fixed point theory for random operators was initiated by A.and O.Hanš in[26–28,37]for the study of random operator equations,and the main difficulty lies in establishing measurability of random fixed points.For the fixed points of contractive random operators,their measurability can be established by successive approximant methods[27].But for the random generalization of topological fixed point theorems like Schauder’s fixed point theorem,the measurability problem can be solved by measurable selection theorems as surveyed in[38];see,for example,[2].The two kinds of methods both heavily depend on the separability of spaces or sets in question.After Bharucha-Reid[2]surveyed the random generalizations of Banach’s and Schauder’s fixed point theorems,he also ever presented the problem of random generalization of fixed point theorems for nonexpansive mappings(see(i)in Section 5 of[2]).Browder-Kirk’s fixed point theorem[4,6,7,31,32]is,without doubt,the most famous one for nonexpansive mappings,which can be stated as follows:Letbe a Banach space,V⊂B a weakly compact convex subset with normal structure and T:V→V a nonexpansive mapping,then T has a fixed point in V.Let(Ω,F,P)be a probability space,(M,d)and(M1,d1)two metric spaces and T:Ω×M→M1a mapping.Let us recall from[1,2,39]:(1)a mapping X:Ω→M1is said to be a random element(or,F-random element)if X−1(G):={ω ∈ Ω :X(ω)∈ G}∈ F for each open set G of M1,furthermore,a random element X is said to be simple if it only takes finitely many values,and X is said to be a strong random element if X is the pointwise limit of a sequence of simple random elements,and it is well known that X:Ω→M1is a strong random element if and only if both X is a random element and its range X(Ω)is a separable subset of M1;(2)T is called a random operator if T(·,x):Ω → M1is a random element for each x ∈ M,furthermore T is called a strong random operator if T(·,x)is a strong random element for each x ∈ M.Then,Bharucha-Reid’s problem can be precisely stated as follows:Letbe a Banach space,V ⊂ B a weakly compact convex subset with normal structure,(Ω,F,P)a probability space,and T:Ω ×V → V a random nonexpansive operator(namely,for eachfor all v1,v2∈ V),then,is there a random element v:Ω → V such that T(ω,v(ω))=v(ω)for almost all ω ∈ Ω?
Lin[34]and Xu[40] first studied Bharucha-Reid’s problem;in particular,Xu[40]partly solved the problem under the assumption that V is a nonempty closed bounded convex separable subset of a reflexive Banach space B such that V has the fixed point property for nonexpansive mappings.It is obvious that T must be a strong random operator when B or V is separable.In this article,we prove that T still has a random fixed point under the weaker assumption that T is only required to be a strong random operator without the requirement that V or B is separable.Our result has an advantage:it includes the classical Browder-Kirk’s fixed point theorem as a special case and thus is also more natural.As compared with Lin[34]and Xu[40],their methods are making use of measurable selection theorems,whereas ours are based on the recent development of the theory of random normed modules(brie fly,RN modules)because measurable selection theorems can no longer apply to the case when B or V is not separable.This article combines measurable selection theorems and the theory of random conjugate spaces so that we can deeply develop the theory of RN modules and further overcome the difficulty with nonseparable spaces.
The success of this article lies in answering the above-mentioned problems in a positive way,in particular our method is a skillful combination of the theory of RN modules,measurable selection theorems,and Banach space techniques.We may hope that this method can be applied in other related aspects.
The remainder of this article is organized as follows:In Section 2 of this article,we give some necessary preliminaries on RN modules and further answer the problems(1)and(2)as above;In Section 3,we prove a general random fixed point theorem for a strong random nonexpansive operator on a Banach space as a better solution to Bharucha–Reid’s problem.
2 Some Necessary Preliminaries on RN Modules and Positive Answers to the Problems(1)and(2)
The main results of this section are Theorems 2.11 and 2.16;let us first give some preliminaries.
Throughout this article,unless otherwise stated,(Ω,F,P)always denotes a given probability space;K the scalar field R of real numbers or C of complex numbers;L0(F,K)the algebra of equivalence classes of K-valued F-measurable random variables on(Ω,F,P),where the scalar multiplication,addition and multiplication operations on equivalence classes are,as usual,induced from the corresponding pointwise operations on random variables;L0(F)simply denotes L0(F,R)andthe set of equivalence classes of extended real-valued F-measurable random variables on(Ω,F,P).
Proposition 2.1 below can be naturally regarded as a randomized version of the well known supremum or infimum principle forand R.
Proposition 2.1([5])Whenis partially ordered by ξ≤ η if and only if ξ0(ω)≤η0(ω)for P-almost all ω in Ω,where ξ0and η0are respectively arbitrarily chosen representatives of ξ and η inis a complete lattice.As usual,and,respectively,stand for the supremum and infimum of a subset H ofFurthermore,the followings hold:

(3)L0(F),as a sublattice ofis Dedekind complete,namely any subset having an upper bound in L0(F)must possess a supremum in L0(F).
As usual,for two elements ξ and η inmeans ξ≤ η andVery often,for any A ∈ F,ξ< η on A means ξ0(ω)< η0(ω)for P-almost all ω in A,where ξ0and η0are arbitrarily chosen representatives of ξ and η,respectively.Letting A={ω ∈ Ω : ξ0(ω)<η0(ω)},we use(ξ< η)for A,which will not produce any confusion,because such sets A only differ by a null set for respectively different choices of ξ0and η0.Similarly,one can understandand so on.
This article always employs the following notations:

In the study of applying the theory of RN modules to the theory of random operators,one often has to distinguish a random variable from its equivalence class.Therefore,this article also mentions an equivalent variant of Proposition 2.1 as follows:
Proposition2.1′([29])Letbe the set of extended real-valued F-random variables on(Ω,F,P).η ∈is called an essential upper bound for a subset H ofif h(ω)≤ η(ω)for P-almost all ω in Ω(brie fly,h ≤ η a.s.)for any h ∈ H.Furthermore,η is called an essential supremun of H if η ≤ η′a.s.for any essential upper bound η′for H.Similarly,one has the notion of an essential lower bound or an essential infimum.Then,every subset H ofhas an a.s.unique essential supremum and infimum,denoted by ess.sup(H)and ess.inf(H)respectively.
Remark 2.2Let L(F)be the set of real-valued F-random variables on(Ω,F,P)and H a subset of L(F).For a real-valued function r:Ω→R,if h≤r a.s.for any h∈H,then it is easy to see ess.sup(H)≤r a.s.,so ess.sup(H)can be taken as an element of L(F),where h ≤ r a.s.means that there is an F-measurable Ω′with P(Ω′)=1 such that h(ω) ≤ r(ω)for any ω ∈ Ω′.
Definition 2.3([9,10,14]) An ordered pairis called a random normed module(brie fly,an RN module)over K with base(Ω,F,P)if E is a left module over the algebra L0(F,K)andis a mapping from E tosuch that the followings hold:
When(Ω,F,P)is trivial,namelyreduces to an ordinary normed space over K.Just as a norm induces the norm topology on a normed space,the L0-norm on an RN moduleinduces a metrizable linear topology on E,called the(ε,λ)-topology.The(ε,λ)-topology has its origin in the theory of probabilistic metric spaces;see[35]for more historical backgrounds.
Proposition 2.4([9,10,14]) Letbe an RN module over K with base(Ω,F,P).For any given positive numbers ε and λ with 0< λ <1,let Nθ(ε,λ)={x ∈ E:P{ω ∈ Ω :called the(ε,λ)-neighborhood of θ,then{Nθ(ε,λ) : ε >0 and 0< λ <1}forms a local base for some metrizable linear topology on E,called the(ε,λ)-topology,denoted byFurthermore,L0(F,K)(as a special RN module,its L0-norm is just the usual absolute value mappingis a topological algebra over K when L0(F,K)is endowed with its(ε,λ)-topology,andis a topological module over the topological algebra L0(F,K).
Example 2.5Letbe a Banach space over K and L0(F,B)the linear space of equivalence classes of B-valued strong F-random elements on(Ω,F,P)under the ordinary scalar multiplication and addition operations on equivalence classes.Then the scalar multiplication on B induces the module multiplication on L0(F,B)as follows:ξx:=the equivalence class of ξ0(·) ·x0(·)for any(ξ,x) ∈ L0(F,K) × L0(F,B),where ξ0and x0are respectively arbitrarily chosen representatives of ξ and x.Furthermore the normon B induces the L0-norm on L0(F,B),still denoted byas follows:=the equivalence class offor any x ∈ L0(F,B),where x0is as above.Then,(L0(F,B),)becomes a-complete RN module over K with base(Ω,F,P).In particular the(ε,λ)-topologyon L0(F,B)is just the topology of convergence in probability on L0(F,B).
To give Example 2.6 below,let us first recall from[1]the notion of a w∗-random element.Let B′be the conjugate space of a Banach space()over K,then a mapping V:(Ω,F,P)→ B′is called a w∗-F-random element if V(·)(b): Ω → K is a K-valued F-random variable on(Ω,F,P)for any b∈ B.Furthermore,two w∗-F-random elements V1and V2:(Ω,F,P)→ B′are said to be w∗-equivalent if V1(·)(b)=V2(·)(b)a.s.for any b ∈ B.
Example 2.6Let L0(F,B′,w∗)be the linear space of w∗-equivalence classes of w∗-F-random elements from(Ω,F,P)to B′under the usual scalar multiplication and addition operations on w∗-equivalence classes.Similar to Example 2.5,L0(F,B′,w∗)is a left module over the algebra L0(F,K)under the module multiplication induced from the scalar multiplication on B′,definedas follows:=the equivalence class of ess.supfor any x ∈ L0(F,B′,w∗),where x0(·)is an arbitrarily chosen representative of x.Then,(L0(F,B′,w∗),)becomes a-complete RN module over K with base(Ω,F,P).Besides,let r:Ω → R be defined byb∈ B and≤ 1},thena.s.for any b∈ B andalthough r is not necessarily F-measurable,ess.sup({|x0(·)(b)|:b∈ B andalways belongs to L(F),sois well defined.
The(ε,λ)-topology is essentially not locally convex;for example,L0(F,K)is the simplest RN module,but there does not exist any nontrivial continuous linear functional on L0(F,K)when F does not contain any atom.The following notion of a random conjugate space is crucial in the subsequent development of RN modules.
Definition 2.7([8,14]) Letbe an RN module over K with base(Ω,F,P).A linear operator f:E → L0(F,K)is said to be a.s.bounded if there exists somesuch thatfor any x∈E.Denote by E∗the linear space of a.s.bounded linear operators from E to L0(F,K),a module multiplication·:L0(F,K)×E∗→E∗is introduced by(ξ·f)(x)= ξ·(f(x))for any(ξ,f)∈ L0(F,K)×E∗,and an L0-normis given byV for any x∈ E}for any f ∈ E∗,thenbecomes an RN module over K with base(Ω,F,P),called the random conjugate space of E.
Now,it is also well known that f∈E∗if and only if f is a continuous module homomorphism fromtoat which timeandseeing[11,14,15]for details.
Lemma 2.8([12]) Let(Ω,F,P)be a complete probability space anda Banach space over K.Define the canonical mapping J:L0(F,B′,w∗) → L0(F,B)∗as follows:for each y ∈ L0(F,B′,w∗),J(y):L0(F,B)→ L0(F,K)is given byfor each x ∈ L0(F,B),whereis the equivalence classdefined byy0(ω)(x0(ω))for each ω ∈ Ω,and x0and y0are a representative of x ∈ L0(F,B)and y ∈L0(F,B′,w∗),respectively.Then,J is an isometric isomorphism from L0(F,B′,w∗)onto L0(F,B)∗(in the sense of RN modules).
Definition 2.9([21]) Let E be a topological module overthe topological algebra(L0(F,K),.A subset G of E is said to be L0-convex if ξx+ ηy ∈ G for any x and y ∈ G and ξ andsuch that ξ+ η=1.Furthermore,an nonempty L0-convex subset G of E is said to be L0-convexly compact(or,to have L0-convex compactness)if any family of nonempty closed L0-convex subsets of G has a nonempty intersection whenever the family has the finite intersection property(namely each of its finite subfamily has a nonempty intersection).
Throughout this article,because every RN module is always endowed with the(ε,λ)-topology,all topological terminologies are with respect to the(ε,λ)-topology,so we no longer mention the(ε,λ)-topology in the sequel of this article.An RN module(E,)over K with base(Ω,F,P)is a topological module over the topological algebra L0(F,K);in particular,we have the following:
Proposition 2.10([21,Theorem 2.21])Let(E,)be a complete RN module over K with base(Ω,F,P)and G a closed L0-convex subset of E.Then,G is L0-convex compact if and only if for each f∈E∗,there exists g0∈G such thatwhere Re(f(g))stands for the real part of f(g).
Proposition 2.10 is,in fact,a random generalization of the famous James’theorem[30],which shows that the notion of L0-convex compactness for a complete RN module plays the same role as weak compactness for a Banach space.Proposition 2.10 directly leads to a positive answer to Problem(1)in the introduction of this article,namely Theorem 2.11 below:
Theorem 2.11Let(B,)be a Banach space over K and V of a closed convex subset of B.Then,L0(F,V)is an L0-convexly compact subset of the complete RN module L0(F,B)if and only if V is weakly compact.Where L0(F,V)is the set of equivalence classes of V-valued strong F-random elements on(Ω,F,P),so it is clear that L0(F,V)is a closed L0-convex subset of L0(F,B).
ProofLet FPbe the completion of F with respect to P,because elements in L0(F,B)are equivalence classes and each B-valued FP-strong random element on(Ω,FP,P)is almost everywhere equal to a B-valued F-strong random element on(Ω,F,P),L0(F,B)and L0(FP,B)are identified,thus we can,without loss of generality,assume that(Ω,F,P)is a complete probability space(otherwise,we consider(Ω,FP,P)instead of(Ω,F,P)).By Proposition 2.10,for the part of sufficiency,we only need to verify that Ref can attain its maximum on L0(F,V)for any given f ∈ L0(F,B)∗.

By Lemma 2.8,there exists y∈ L0(F,B′,w∗)such that f(v)=hv,yi for each v∈ L0(F,B).Furthermore,letbe an arbitrarily chosen representative of xnfor each n∈N and y0an arbitrarily chosen representative of y,then it is obvious thatis a representative ofand ξ0: Ω → (−∞,+∞),defined byfor each ω ∈ Ω,is a representative of
If we can prove that there exists a V-valued F-strong random element v0defined on(Ω,F,P)such thatfor each ω ∈ Ω,thenwe will complete the proof of this theorem,where v is the equivalence class of v0.For this,letthen L is a separable complete subspace of B because eachis a separable subset of B by the strong measurability offurther define a multifunctionfor each ω ∈ Ω,then each F(ω)is a closed convex subset of V,and hence each F(ω)is a weakly compact convex subset of V.
Now,we prove that F is measurable,namelyfor each open subset G of L.In fact,let Q be the set of rational numbers in[0,1],for each n ∈ N,thenis an at most countable set of V-valued F-strong random elements,denoted by{vn,n ∈ N}.It is also clear thatfor each ω ∈ Ω,and thus F is measurable.
Necessity.Let L0(F,V)be L0-convexly compact and f ∈ B′,then f induces an elementas follows:=the equivalence class of f(x0(·))for any x∈L0(F,B),where x0(·)is an arbitrarily chosen representative of x.Then,by Proposition 2.10,there exists some g0∈L0(F,V)such thatIt is easy to check thatis the equivalence class of the constant function with its value equal to sup{Re(f(v)):v∈V},further letting g0be an arbitrarily chosen representative of g0yields Re(f(g0(ω)))=sup{Re(f(v)):v ∈ V}for almost all ω in Ω.Because the L0-convex compactness of L0(F,V)obviously implies the a.s.boundedness of it,namelyand as it is also easy to check thatis the equivalence class of the constant function with its value equal to sup{kvk:v∈V},thennamely V is a bounded set.Thus,g0is Bochner-integrable.letthenTo sum up,V is weakly compact by the famous James’theorem[30].
Let us recall that a nonempty closed convex subset V of a Banach spaceis said to have normal structure if for each bounded closed convex subset H of V with Diam(H):=there exists at least one point h0of H such thath∈H} In[20],we proved that every closed L0-convex subset of a random uniformly convex RN module has random normal structure.Specially,for a closed convex subset V of a uniformly convex Banach space B,L0(F,V)has random normal structure.In this article,we prove Theorem 2.16 below,which answers Problem(2)in Introduction of this article.To prove it,we first give Definition 2.13,and Lemmas 2.14 and 2.15 below. Lemma 2.14[20]Letandbe two complete RN modules over K with base(Ω,F,P)(at this time E and E1both are σ-stable[14,20]).G ⊂ E a nonempty subset and T:G → E1an L0-Lipschitz mapping(namely,there existssuch thatfor all x and y ∈ G).Then,when G is σ-stable,T is σ-stable(and hence,T(G)is also σ-stable),namelyfor each sequence{gn:n∈N}in G and each countable partition{An:n∈N}of Ω to F. Lemma 2.15([20]) Let G be a σ-stable subset of L0(F)such that G has an upper(lower)bound ξ∈ L0(F),then for eachthere exists some gε∈ G such thaton Ω (correspondingly, Theorem 2.16Letbe a Banach space over K and V ⊂B a weakly compact convex subset with normal structure.Then,L0(F,V),as a closed L0-convex subset of L0(F,B),has random normal structure. ProofAs in the proof of Theorem 2.11,we can assume that(Ω,F,P)is a complete probability measure space. So,for any x∈conv{xk,k∈N},converges a.e.to D(H),which also means thatfor any x∈conv{xk,k∈N}.Furthermore,it is also clear thatfor any x∈conv{xk,k∈N}. Now,arbitrarily choosing a representativeof xnfor each n∈N,let{vn,n∈N}be constructed as in the proof of Theorem 2.11,thenfor each n ∈ N and for almost all ω ∈ Ω.We can,without loss of generality,assume thatfor each n ∈ N and each ω ∈ Ω.Letand define F:Ω → 2Lbyfor each ω ∈ Ω,then L is a complete separable subspace of B and each F(ω)is a closed convex subset of V.Becausefor each ω ∈ Ω,it is obvious that for each ω ∈ Ω and for each u ∈ F(ω).This means that each F(ω)does not possess any nondiametral point,which contradicts the fact that V has normal structure. Remark 2.17The idea of constructing the sequence{xn,n∈N}in the proof of Theorem 2.16 is motivated fromand Mil’man’s work[3].Normal structure of Banach spaces was deeply studied in[3,33,36];in particular Smith and Turett proved in[36]that a Banach space X has normal structure if and only if the Lebesgue-Bochner function space Lp(µ,X)has normal structure for any given p such that 1 The main result of this section is Theorem 3.2,which provides a best solution to Bharucha-Reid’s problem,and is based on a fixed point theorem recently obtained in[20]as follows: Proposition 3.1([20]) Letbe a complete RN module over K with base(Ω,F,P)and G⊂E an L0-convexly compact L0-convex subset with random normal structure.Then,every nonexpansive mapping T from G to G(namelyfor all u,v∈G)has a fixed point in G. Theorem 3.2Letbe a Banach space over K and V of a weakly compact convex subset of B such that V has normal structure,then every strong random nonexpansive operator T:(Ω,F,µ)× V → V has a strong F-random element x0(·): Ω → V such that T(ω,x0(ω))=x0(ω)for almost all ω ∈ Ω. ProofBy Theorems 2.11 and 2.16,L0(F,V)has both L0-convex compactness and random normal structure.Furthermore,T induces a nonexpansive mapping:L0(F,V)→L0(F,V)in a natural manner:for each given x∈L0(F,V),arbitrarily choosing a representative x0of x,then we defineas the equivalence class of T(·,x0(·)),then T(·,x0(·))is a V-valued strong F-random element because T is nonexpansive(and thus also continuous)and a strong random operator,so thatis well defined.Applying Proposition 3.1 toand L0(F,V)produces some x∈L0(F,V)such that(x)=x,then an arbitrarily chosen representative x0of x must satisfy T(ω,x0(ω))=x0(ω)for almost all ω ∈ Ω. Remark 3.3Up to now,Theorem 3.2 also provides a most general partial answer to the question posed by Xu in Remark 1 of[40],namely,in the general case of Theorem 3.2,the assumption that F is closed under the Suslin operation is indeed superfluous. Corollary 3.4Let S be a nonempty closed convex subset of a uniformly convex Banach space X and f:Ω ×S → S a nonexpansive strong random operator such that f(ω,S)is bounded for any ω ∈ Ω.Then,f has a strongly measurable random fixed point. ProofLet r:Ω → [0,+∞)be the real-valued function defined bys ∈ S},then for each S-valued F-strong random element x0:Ω → S,f(·,x0(·))is an S-valued strong F-random element because f is a nonexpansive strong random operator,furthermore,we also havefor each ω ∈ Ω.Denotingis an S-valued and strong F-random element},then ξ0is a nonnegative real-valued F-random variable on(Ω,F,P)and ξ0(ω) ≤ r(ω)for almost all ω ∈ Ω. Corollary 3.5Let S be a nonempty closed convex subset of a Hilbert space X and f:Ω ×S → X a nonexpansive strong random operator such that f(ω,S)is bounded for any ω ∈ Ω.Then,there exists an S-valued strong F-random element ϕ : Ω → S such thatfor almost all ω ∈ Ω.Further,ϕ is also a random fixed point of f if f satisfies,in addition,one of the following two conditions: (i)For each ω ∈ Ω and each x ∈ S withthere exists y,depending on ω and x,in IS(x)={x+c(z−x):z∈ S and c≥ 0}such that ProofLet p:X→S be the usual proximity mapping,then p◦f:Ω×S→S is a nonexpansive strong random operator such thatis bounded for any ω ∈ Ω.By Corollary 3.4,has an S-valued F-strongly measurable random fixed point ϕ,which satisfiesfor almost all ω ∈ Ω.The remaining part of this proof may proceed as in the proof of Theorem 4 of[34].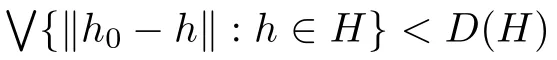

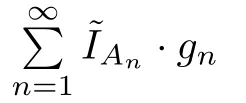






3 A General Random Fixed Point Theorem for a Nonexpansive Strong Random Operator

 Acta Mathematica Scientia(English Series)2020年2期
Acta Mathematica Scientia(English Series)2020年2期
