ASYMPTOTIC BEHAVIOR OF SOLUTIONS FOR THE CHAFEE-INFANTE EQUATION∗

School of Mathematics and Big Data,Foshan University,Foshan 528000,China

E-mail:huanghc@m.scnu.edu.cn

Rui HUANG

School of Mathematical Sciences,South China Normal University,Guangzhou 510631,China

E-mail:huang@scnu.edu.cn

Abstract In higher dimension,there are many interesting and challenging problems about the dynamics of non-autonomous Chafee-Infante equation.This article is concerned with the asymptotic behavior of solutions for the non–autonomous Chafee-Infante equation λ(t)(u−u3)in higher dimension,where λ(t)∈ C1[0,T]and λ(t)is a positive,periodic function.We denote λ1as the first eigenvalue ofFor any spatial dimension N ≥ 1,we prove that if λ(t)≤ λ1,then the nontrivial solutions converge to zero,namely,x ∈ Ω;if λ(t)> λ1as t → +∞,then the positive solutions are “attracted” by positive periodic solutions.Specially,if λ(t)is independent of t,then the positive solutions converge to positive solutions of−∆U= λ(U−U3).Furthermore,numerical simulations are presented to verify our results.

Key words Chafee-Infante equation;asymptotic behavior;periodic solutions

1 Introduction

We are concerned with the asymptotic behavior of solutions for Chafee-Infante equation

complemented with initial condition

where Ω ⊂ RNis a bounded domain with smooth boundary,and g(x) ∈We are also concerned with the existence of periodic solutions for the problem(1.1)–(1.2)complemented with periodic condition

where T is a positive constant,λ(t)is a positive function,and

In one dimension,if λ(t)is independent of t,then(1.1)is autonomous Chafee-Infante equation,which is well-known and famous because of the fact that it is a very good example of an equation generating an infinite dimensional dynamical system for which the structure of the global attractor,and then the long-term dynamics of solutions,has been described in detail;see[1,p.2357],[7,Section 4.3],[8,Section 5.3],[16,Section 11.5]and[19],and so on.The extension of such results to the non-autonomous equation is a very interesting and challenging problem.If λ(t)depends on t,then problem(1.1)–(1.3)admits positive solutions and sign changing periodic solutions,seeing[10];bounded solutions of the problem(1.1)–(1.3)always“attracted”by periodic solutions,seeing[3,Theorem C],seeing also[2,Chapter 13],[16]and the survey[14,Section 4]about the asymptotic of solutions for

In higher dimension,to fully understand the dynamics of non-autonomous Chafee-Infante equation(1.1),there are still many open questions,such as the existence and asymptotic of sign changing solutions,the structure of the global attractor;see[1,p.2372]and[2,p.338].To our best knowledge,there are only a few references about asymptotic behavior of solutions for(1.1)–(1.3)in higher dimension;see[4].Partly because the asymptotic behavior of solutions becomes very complex,some methods such as Poincaré-Bendixson theorem,zero number properties[10,p.1]cannot be easily adopted for problem(1.1)–(1.3)in higher dimension.

In this article,under suitable assumption,we prove that the periodic solutions and equilibrium solutions are the “attractors”of problem(1.1)–(1.3).Our results are valid for any spatial dimension N≥1.In some sense,our results are nontrivial,because in higher dimension,all bounded solutions“attracted” by periodic solutions does not hold in general;see[9,p.574],[12,p.14],[14,Section 6],and[15].

Let λ1,ϕ1be the first eigenvalue and corresponding eigenfunction of

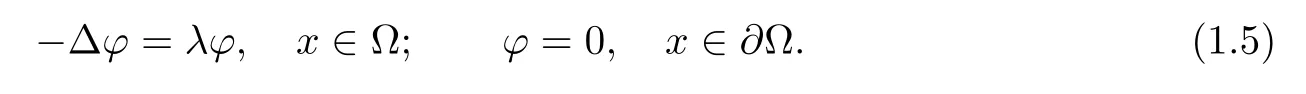
The following assumption will be used in our proof:

Now,we state the main results of this article.

Theorem 1.1Assume that(1.6)–(1.7)hold,then problem(1.1)–(1.3)admits nontrivial global classical solutions.

Theorem 1.1 shows the existence of nontrivial solutions,then in Theorem 1.2(ii)and Theorem 1.3(ii)below,we study the time asymptotic behavior of the solutions.

Theorem 1.2Assume that(1.6)–(1.7)hold.

(i)If λ(t)≤ λ1,then problem(1.1)–(1.2)complemented with(1.4)has only zero solution.

(ii) If λ(t) ≤ λ1,then the nontrivial solutions of problem(1.1)–(1.3)converge to zero,namely,

Note that if u is a solution of problem(1.1)–(1.2)complemented with(1.4),then −u is also a solution;“nontrivial solutions” may include positive solutions,negative solutions,and sign changing solutions.If λ(t) ≤ λ1,Theorem 1.2 implies that the zero solution of problem(1.1)–(1.2)complemented with(1.4)is“stable” and “ attracting” .In Theorem 1.3,the hypothesis λ(t)> λ1holds for every t.

Theorem 1.3Assume that(1.6)–(1.7)hold.

(i)If λ(t)> λ1,then problem(1.1)–(1.2)complemented with(1.4)has a positive periodic u∗(x,t).

(ii)If λ(t)> λ1,then problem(1.1)–(1.3)admits positive classical solution u(x,t),which satisfies

Furthermore,similar to Pao[13,p.432,(3.11)],under the additional assumption u∗(x,0)≤g(x),then

where u∗(x,t)is the positive periodic solution of(1.1)–(1.2)complemented with(1.4).

Specially,if λ(t)is independent of t,then problem(1.1)–(1.3)becomes

If λ ≤ λ1,then Theorem 1.2(ii)implies that nontrivial solutions of the problem(1.8)–(1.10)converge to zero.For the case λ > λ1,we have the following result.

Theorem 1.4Assume that λ > λ1and g(x)>0,x ∈ Ω,then problem(1.8)–(1.10)admits positive solution u(x,t),such that

where U(x)is a positive solution of

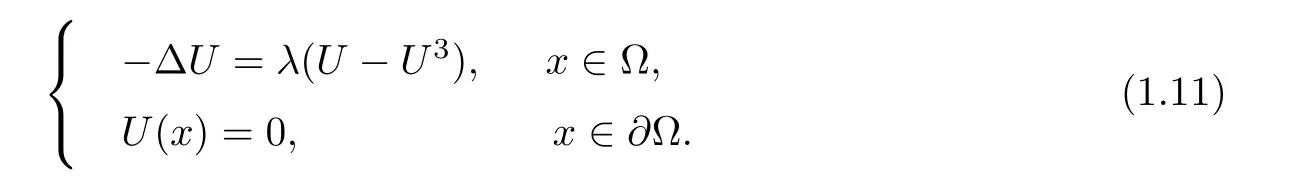
The rest of this article is organized as follows.In Section 2,we are devote to proving the main results.Finally,in Section 3,we present some numerical simulations to verify our results.

2 Proof of Main Results

2.1 Proof of Theorem 1.1

We will use the following lemma to prove the existence of nontrivial solutions for problem(1.1)–(1.3).

Lemma 2.1(Leray-Schauder Fixed Point Theorem)(see[20,p.277])Let B be a Banach space and F(u,σ)be a mapping from B × [0,1]to B satisfying the following conditions:

(i)F is a compact mapping;

(ii)F(u,0)=0,∀u ∈ B;

(iii)There exists a constant C>0,such that for any u ∈ B,if F(u,σ)=u for some σ∈[0,1],then

Then,the mapping F(u,1)has a fixed point,that is,there exists u∈B,such that F(u,1)=u.

For any τ>0,we choose the Banach space B as follows:

For any v∈B,0≤σ≤1,we consider the following problem

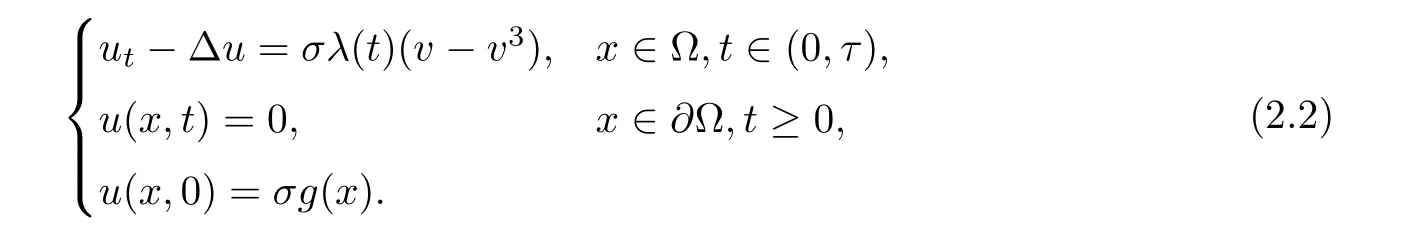
Now,we give the definition of weak solution;see[20,p.40,p.72]for details.

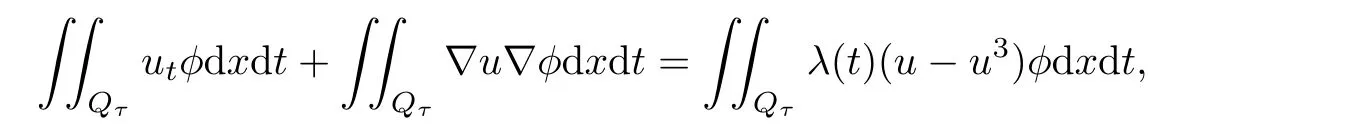
We define the mapping

As v∈B,then v3is uniformly bounded inthusAccording to the Lpestimates for linear parabolic equations(see[20,Theorem 9.2.5]),problem(2.2)admits a unique weak solutionTherefore,the mapping F is well defined.

Proposition 2.3For any u ∈ B,if F(u,σ)=u for some σ ∈ [0,1],thenand

ProofIfthen u is the solution of

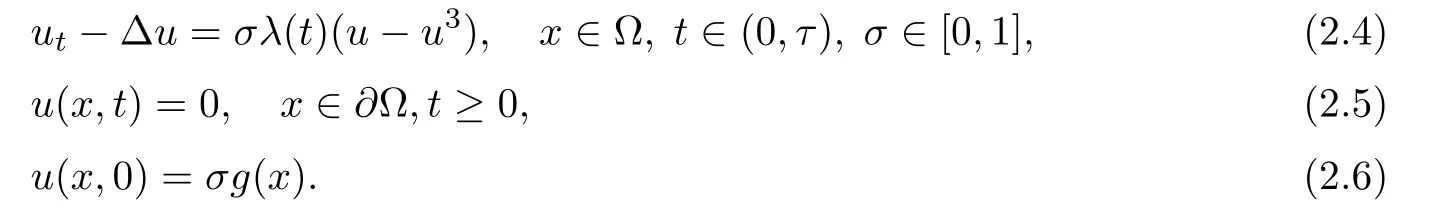
Obviously,problem(2.4)–(2.6)with σ =0 only admit solution u ≡ 0,thus F(u,0)=0.We are concern with the existence of nontrivial solutionthus we consider the case 0<σ≤1.Multiplying equation(2.4)by u,integrating by part over Ω,and using(2.5),we have

Assumption(1.6)implies that λ(t)is bounded.By Cauchy inequality,then

and in this article,C is a positive constant independent of u,though C may vary from step to step.By(2.7)and(2.8),then

The first eigenvalue λ1is given by the following formula(see[5,p.489])

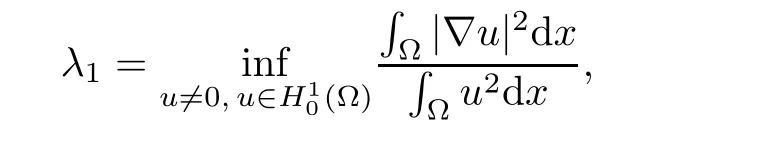
then

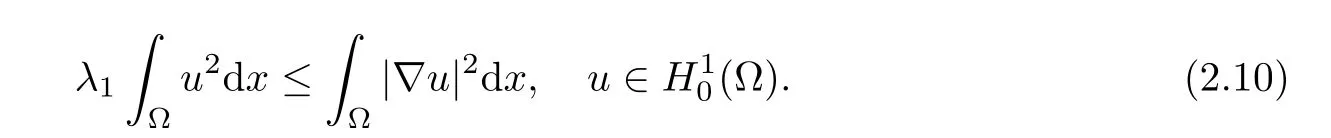
By(2.9)and(2.10),then

By Gronwall’s inequality,(2.11)implies that

Multiplying equation(2.4)by u3,integrating by part over Ω,and using(2.5),we have

Neglecting the nonnegative termin(2.13),we have

By(2.14)and(2.15),we have

By Gronwall’s inequality,(2.16)implies that u is bounded in

To obtain some necessary estimates,we might assume that the weak solution is appropriately smooth,because the same result can be obtained through an approximate process by considering a related regularized problem.Multiplying equation(2.4)by−∆u,integrating by part over Ω,by Cauchy inequality,then

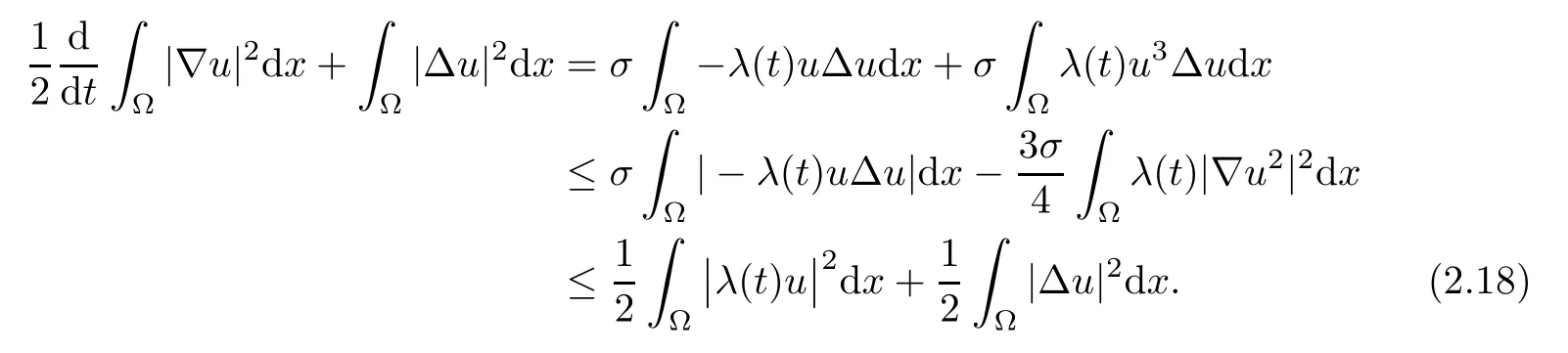
For any finite τ>0,integrating(2.19)over[0,τ],we have

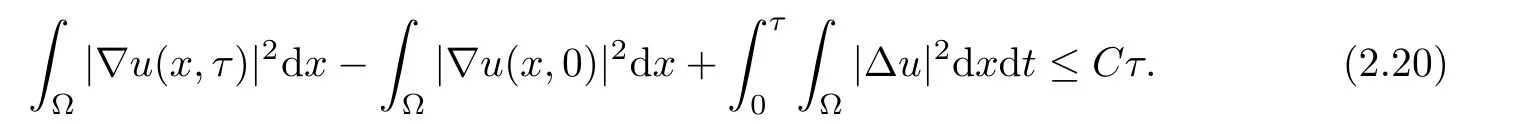
Proof of Theorem 1.1Now,we check that the mapping F in(2.3)satisfies the conditions of Lemma 2.1.

(i)Multiplying equation(2.4)by utand integrating by part over Ω,we have

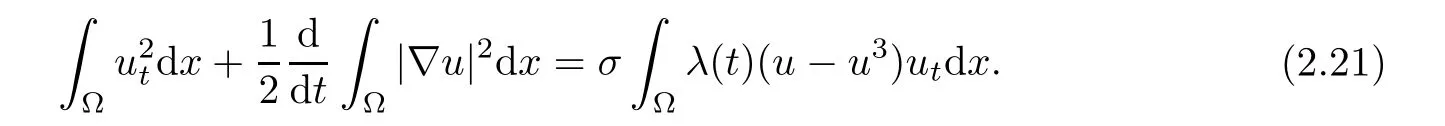
Note that

By assumption(1.6),λ(t)∈ C1[0,T],then λ′(t)∈ C[0,T],and by extreme value theorem,is bounded in[0,τ].By(1.7),(2.17),and(2.23),we have

We denote

By Proposition 2.3 and(2.24),if F(u,σ)=u,then u ∈ W.Note that the embeddingandare compact.By Aubin-Lions lemma(see[21,p.97]),the imbedding from W into B is compact,where B is defined in(2.1),thus the mapping F is compact.

(ii)Obviously,problem(2.2)with σ =0 only admit solution,thus F(v,0)=0.

Integrating(2.7)with σ=1,we have

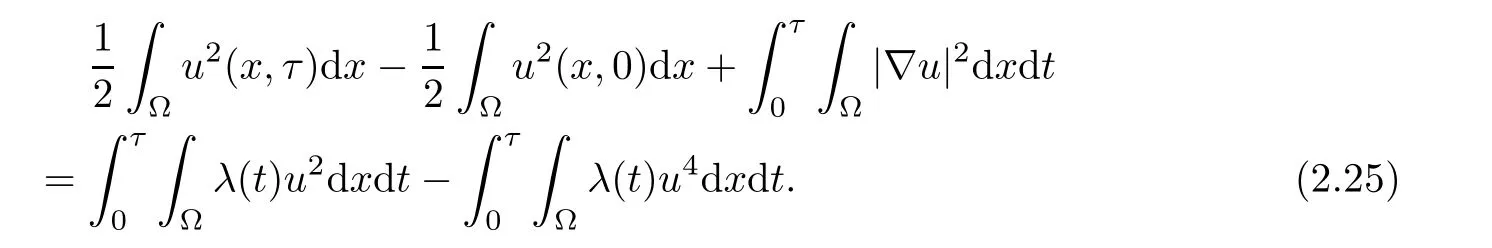
By Proposition 2.3 and(2.24),we have

By the Lpestimates for parabolic equations(see[20,Theorem 9.2.5]),problem(1.1)–(1.3)admits a unique solutionBy Sobolev embedding inequality(see[20,p.27]),

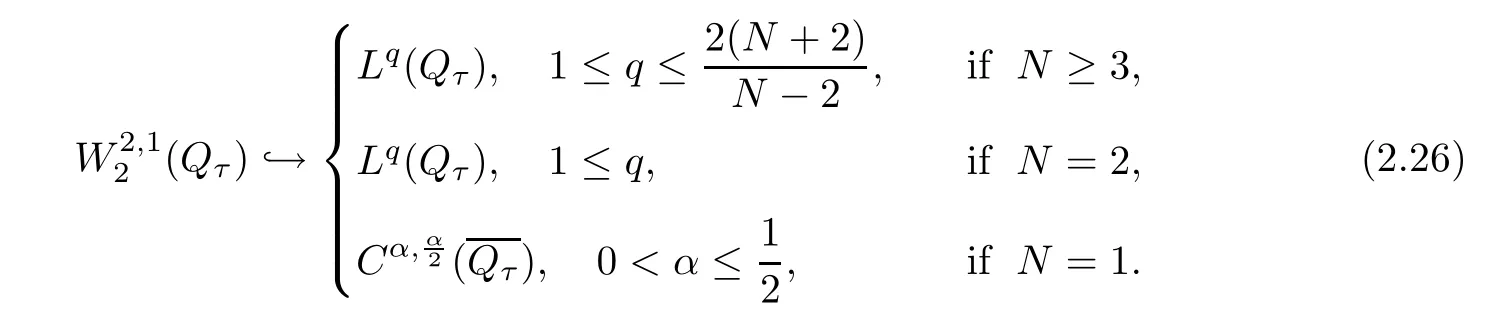
By(2.26),if N=1,then we haveNow,we consider the case N ≥ 2,and we will prove that

We might assume that the weak solution is appropriately smooth,because the same result can be obtained through an approximate process by considering a related regularized problem.Multiplying equation(1.1)bywhere q is defined in(2.26),and integrating by part,then

Integrating(2.27)over[0,τ],we have

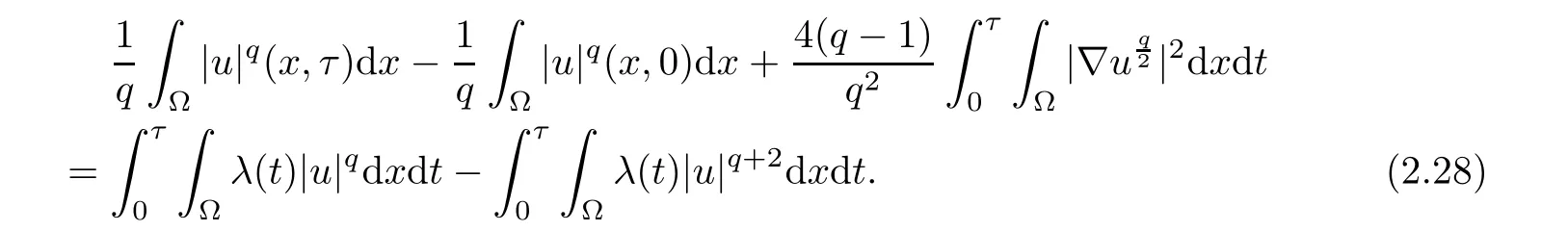
By(2.26),u∈ Lq(Qτ),then(2.28)implies thatSimilar to the process of(2.27)–(2.28),by induction,we infer thatthenBy the Lpestimates for parabolic equations(see[20,Theorem 9.2.5]),then.By Sobolev embedding,thenand the Schauder estimates(see[20,Theorem 8.3.1])implies that the solutionthen we finally obtain the global classical solution for problem(1.1)–(1.3).Hence,the Proof of Theorem 1.1 is complete.

2.2 Proof of Theorem 1.2(i)

If u is a solution of problem(1.1)–(1.2)complemented with(1.4),by(1.4),we have

Multiplying equation(1.1)by u,integrating over[0,T],and using(2.29),we obtain

In view of(2.30),integrating by part over Ω,then we use(2.10)to have

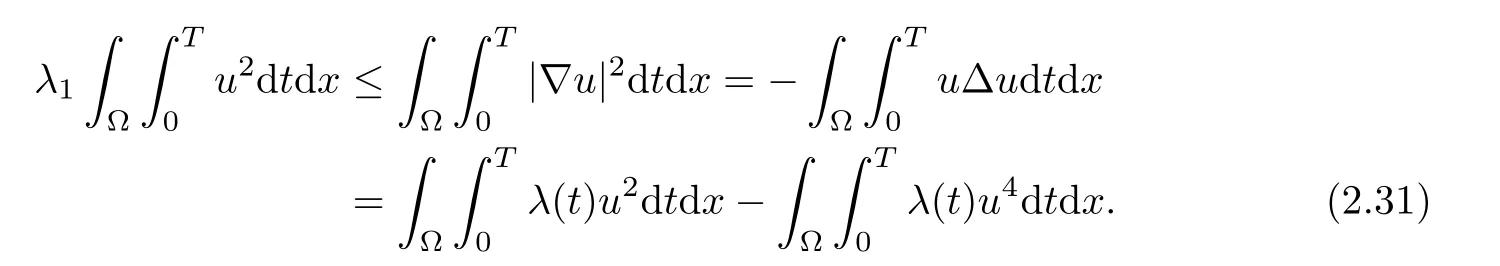
By the assumption λ(t)≤ λ1and(2.31),then

By assumption(1.6),λ(t)is positive,then(2.32)implies that

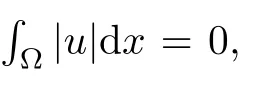
2.3 Proof of Theorem 1.2(ii)

Now,we give the definition of upper and lower solution.

Definition 2.4A functioninis called “upper solution”of problem(1.1)–(1.3),if

Replacing “≥” by “≤” in(2.34)–(2.36),it follows the definition of“lower solution”,denoted byA pair of lower solutionand upper solutioninis called “ordered”,if they satisfy

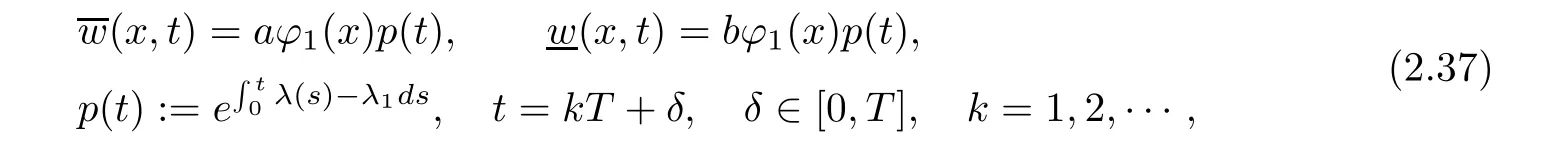
where ϕ1(x)is the first eigenfunction of(1.5),and the constants a,b satisfy

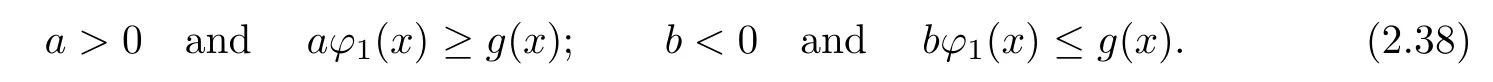
By Theorem 1.1,problem(1.1)–(1.3)admits a nontrivial global classical solution u(x,t).Recalling Definition 2.4,it is easy to check thatare the ordered upper and lowering solution of problem(1.1)–(1.3),thenseeing[20,p.324].

We recall(2.37),t=kT+δ,by(2.39)and(2.40),then

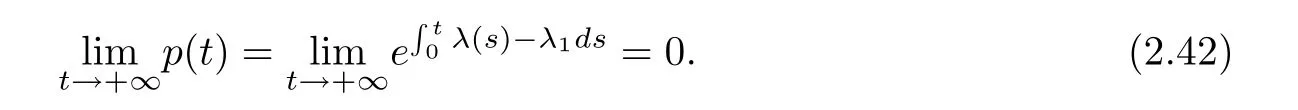
In view of(2.37),because ϕ1(x)is bounded,by(2.42),if λ(t) ≤ λ1,we have

The proof of Theorem 1.2(ii)is complete.

2.4 Proof of Theorem 1.3

We will prove Theorem 1.3 by monotone method;see[20,Chapter 12]for details.Let Λ1,Ψ1be the first eigenvalue and the corresponding eigenfunction of the problem

where Ω ⊂⊂ Ω∗.We choose a positive constantand define the upper solution

Lemma 2.5Assume g(x)>0,x ∈ Ω,then problem(1.1)–(1.3)admits upper solutionwhereis as in(2.45).

ProofNow,we verify thatsatisfies Definition 2.4.Note thatsee[5,p.350]for proof.Because Ω ⊂⊂ Ω∗,then Ψ1>0,x ∈ ∂Ω andthussatisfies(2.35).Becausethen g(x)is bounded.By(2.45),thenthussatisfies(2.36).

Now,we consider the following linear parabolic problem

where the positive constant M is sufficiently large,and φ(x,t)satisfies

By the Schauder theory(see[20,p.250]),for any giventhen(2.47)admits a unique solutionand the following mapping is well defined

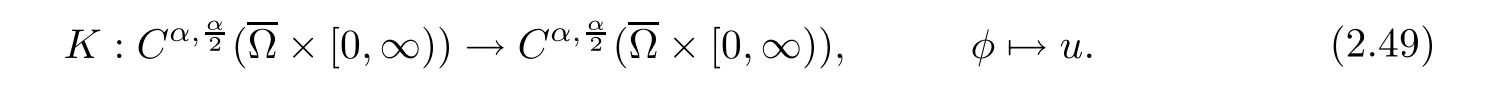
We say that Kφ=u if u is a solution of problem(2.47).

Lemma 2.6If φ1,φ2satisfy(2.48)and φ2≤ φ1,then Kφ2,Kφ1satisfying(2.48)and Kφ2≤Kφ1.

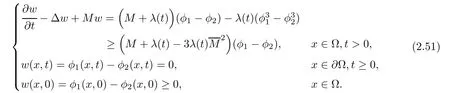
Because φ1− φ2≥ 0,we choose the constant M sufficiently large,such that

By maximum principle,then the solution of problem(2.51)satisfies

Proposition 2.7Assume that(1.6)–(1.7)hold.If g(x)>0,x ∈ Ω,then the global classical solution of problem(1.1)–(1.3)satisfies u(x,t)>0,x ∈ Ω,t≥ 0.

ProofBy Theorem 1.1,problem(1.1)–(1.3)admits global classical solution u.Note that λ(t)(u2−1)is bounded,then there exist a sufficient large constant η,such that λ(t)(u2−1)+η >0.We make a change of variable u(x,t)=eηtw(x,t),then problem(1.1)–(1.3)becomes

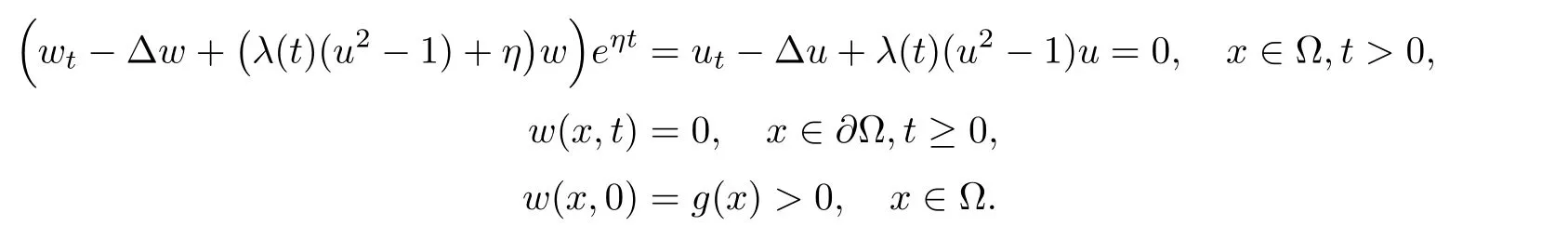
We argue by contradiction.Suppose on the contrary that u attain the minimum at the pointthen w(x0,t0)=0,by strong maximum principle(see[6,p.397]),then w(x,t)≡ 0,which is a contradiction,therefore w(x,t)>0,x∈Ω,t≥0,thus u(x,t)>0,x∈Ω,t≥0.

Proof of Theorem 1.3(i)We denoteand define upper solution sequenceof problem(1.1)–(1.3)as follows:

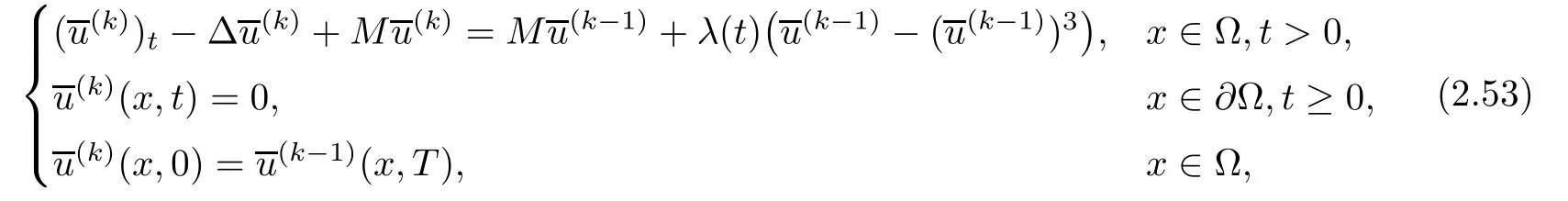
Proposition 2.7 implies thatis positive.By Schauder theory and(2.49),then

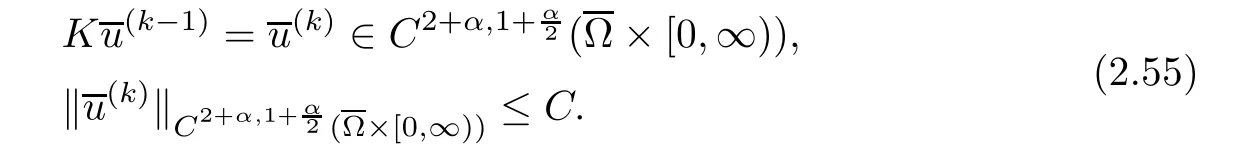
The Sobolev embedding

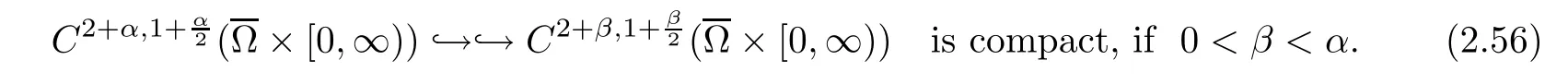
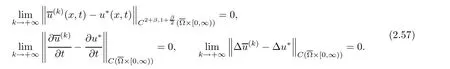
By(2.57),as k→+∞,then(2.53)becomes

Proof of Theorem 1.3(ii)By Theorem 1.1 and Proposition 2.7,problem(1.1)–(1.3)admits a global classical positive solution u(x,t).Using Lemma 2.6,by induction,we infer that

where u∗(x,t)is the positive periodic solution of(2.58);u(x,t+kT)is the solution of problem(1.1)–(1.3).

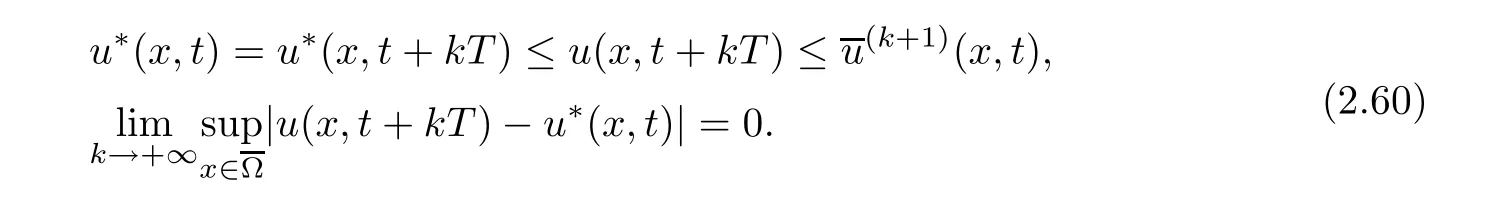
The proof of Theorem 1.3(ii)is complete.

2.5 Proof of Theorem 1.4

Noting that f(u)= λ(u−u3)is an analytic function in u,Simon[18]proved that the solution of(1.8)–(1.10)converges to the equilibrium solution.It is worthwhile to mention the interesting result of Poláčik and Rybakowski[15]:they construct a counterexample to show the analyticity assumption on f(u)is essential.Jendoubi[11]give a new and easier proof for the convergence result of Simon[18];see also Zheng[21,Section 6.3]for details.In this article,we remove the assumption that spatial dimension N≤3 in Zheng[21,p.236],seeing Theorem 1.1 above.For the convenience of reader,the full proof is sketched as follows.

Multiplying equation(1.8)by ut,then integrating over Ω yields

The function

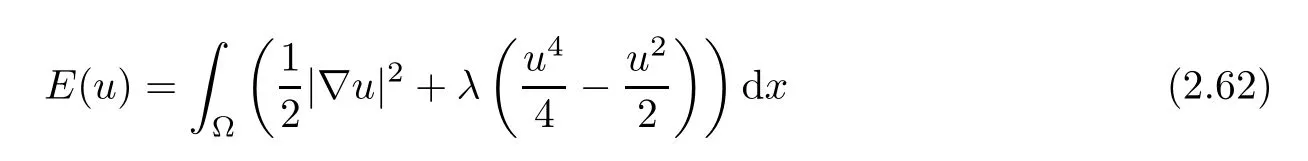
Problem(1.8)–(1.10)defines a “gradient system”,therefore,it follows from[21,Theorem 6.3.2]that for any given initial datumthe ω-limit set ω(g(x))consists of equilibria.Hence,there exist U∈ω(g(x))and a sequence tn,such that

Because E(u(x,t))is decreasing in t,from(2.64)we also have E(u(x,t))≥E(U(x)),and we distinguish two cases as follows.

Case 1E(u(x,t0))=E(U(x))for t0∈R+.Integrating(2.63)on[t0,t],we have

by(2.65),for all t≥t0,then ut=0,which implies that the solution u is in fact a stationary point,so it has to be equal to U(x).

Case 2E(u(x,t))>E(U(x))for all t≥0.

By(1.8)and(2.63),we have

By the Lojasiewicz-Simon inequality stated in[21,Lemma 6.3.4],then

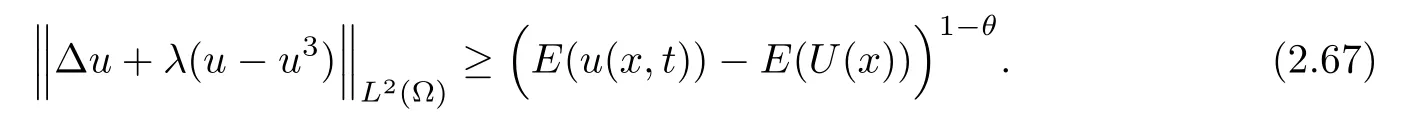
By(2.66)and(2.67),we have

Integrating(2.68)on[tn,t],then using E(u(x,t))>E(U(x)),we have

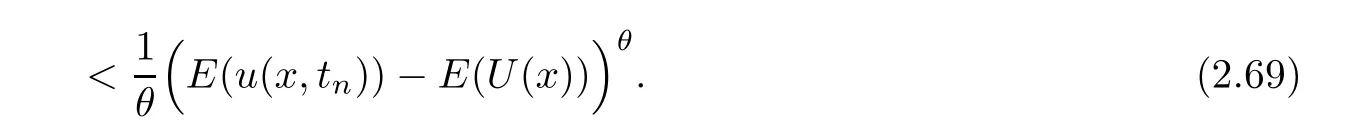
By(2.64)and(2.69),we have

Hence,the proof of Theorem 1.4 is complete.

3 Numerical Simulations

In this section,we will implement numerical simulations to verify our results.For simplicity,in one dimension,we choose Ω =(0,π),then the first eigenvalue of(1.5)is λ1=1.In two dimension,let Ω =(0,a)× (0,b),the eigenvalue and corresponding eigenfunction of(1.5)are

where cmnis a constant.By(3.1),forthen λ11=2.

We use the method of lines(MOL)for solving problem(1.1)–(1.3).The basic idea of the MOL is to replace the spatial derivatives in the PDE with algebraic approximations.The spatial derivatives can be approximated by finite element method,then we have a system of ODEs that approximate the original PDE;see[17]and[10,Section 4.2]for details.

3.1 The verification of Theorem 1.2

In this subsection,we choose g(x)and g(x,y)for(1.3)as follows:

We choose g as in(3.2)and choose λ(t)as follows:

By Theorem 1.2(ii),the nontrivial solutions of problem(1.1)–(1.3)converge to zero;see Figure 1 and Figure 2.

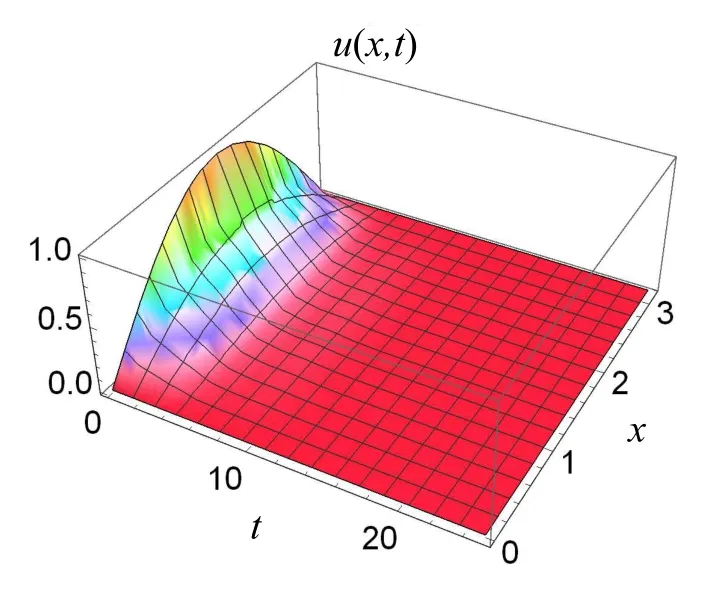
Figure 1 λ(t)=0.6+0.4sin(t)≤ λ1,u(x,t)converges to zero

Figure 2 λ(t)=1.2+0.8sin(t)≤ λ11,u(x,y,t)converges to zero

3.2 The verification of Theorem 1.3

We choose λ(t)as follows:

By Theorem 1.3(ii),as t→ +∞,the positive solutions of problem(1.1)–(1.3)are“attracted”into any small neighborhood of the set of positive periodic solutions of problem(1.1)–(1.2)complemented with(1.4);see Figure 3 and Figure 4.

Figure 3 λ(t)=2.1+sin(t)> λ1,t∈ [0,6π],u(x,t)is“attracted” by positive periodic solution with period 2π

Figure 4 λ(t)=3.1+sin(t)> λ11,λ(t)makes 3 cycles because t∈ [0,6π].There are 3 green“ellipsoid”,which implies that u(x,y,t)is“attracted” by periodic solution with period 2π

3.3 The verification of Theorem 1.4

We choose g as in(3.2)and choose λ for(1.8)as follows:

By Theorem 1.4,then problem(1.8)–(1.10)admits positive solutions,which converge to positive solution U of(1.11);see Figures 5–8.

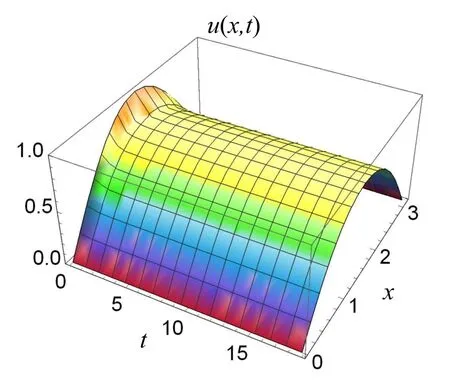
Figure 5 λ=2>λ1,u(x,t)converges to solution U(x)of(1.11)with λ =2,x ∈ (0,π)

Figure 6 λ=3>λ11,u(x,y,t)converges to solution U(x,y)of(1.11)with λ =3

Figure 7 Positive solution U(x,y)of the problem(1.11)with λ=3

Figure 8 U(x,y)− u(x,y,t)with t=6π,where U(x,y)is the positive solution of(1.11)with λ=3;u(x,y,t)is the positive solution of(1.8)–(1.10)with λ =3