SMA复合材料变截面结构的静态非线性有限元分析
孙双双,丁钟宇,武 丹
(青岛科技大学机电工程学院,山东 青岛 266061)
风力机叶片是将风能转换成电能的关键部件,其对风电系统的安全可靠工作起着重要作用。为降低发电成本,风力机叶片逐渐向大型化、轻质化、柔性化方向发展,导致叶片在重力、气动力、惯性力等载荷作用下极易产生较大变形,呈现出几何非线性,严重影响其安装和使用[1]。
借助于航空航天领域“智能材料与结构”[2]的概念,将智能材料用作传感器、驱动器、控制器等安装在风力机叶片中所构成的“智能叶片”[3-4],因具有自适应、自调节、自控制等功能,为风力机叶片变形及振动控制提供了新思路,成为国内外学者近年来研究的热点[5]。如:KIM等[6]将光纤光栅传感器嵌入到风力机叶片中进行了叶片静态和动态特性测试。CHOI等[7]将光纤光栅传感器安装在叶片抗剪腹板内,利用测得的应力来计算叶尖挠度。刘姝等[8]利用压电材料制成的智能驱动器和传感器,实现对风力机叶片振动主动控制。乔印虎等[9]设计了内嵌压电纤维的智能风力机复合材料叶片,并对智能叶片进行了振动主动控制研究。杜向红[10]将风力机叶片简化为等截面细长薄壁梁,并将形状记忆合金(shape memory alloys,SMA)纤维埋入薄壁梁,研究了温度激励下SMA纤维对于薄壁梁变形特性及自由振动特性的影响规律。
目前,基于智能材料对风力机叶片的变形和振动进行控制的研究大多限于主动控制方式,而且理论建模时基本都将风力机叶片简化为等截面梁。由于对风力机叶片进行主动控制时需要外加能源或附加主动控制装置,且利用SMA对其进行主动控制时还存在响应速度慢等缺点,因此本文在前期研究[11-12]的基础上,将风力机叶片简化为复合材料变截面结构,利用SMA的伪弹耗能特性对风力机叶片的静变形进行被动控制研究。理论建模时不仅考虑了SMA的相变特性及材料非线性,而且还考虑了复合材料结构变形的几何非线性。
1 理论分析
内嵌SMA纤维的等厚度复合材料变截面结构如图1所示。为便于分析,建立的空间直角坐标系也如图1所示。SMA纤维沿纵向均匀铺设在复合材料变截面结构顶层和底层的中面。图1中,b1和b2分别表示复合材料变截面结构左右两个横截面的宽度;ht,hb和hc分别表示顶层、底层和中间层的厚度。若该变截面结构的长度用L表示,则沿长度方向任一位置x处的横截面宽度b(x)为:b(x)=b1-(b1-b2)x/L。
假设该复合材料结构发生变形时y方向的位移为零,x和z方向的位移不沿宽度变化。当该复合材料结构受横向载荷作用时,任意一点的纵向位移u按照经典层合梁理论可表示为:
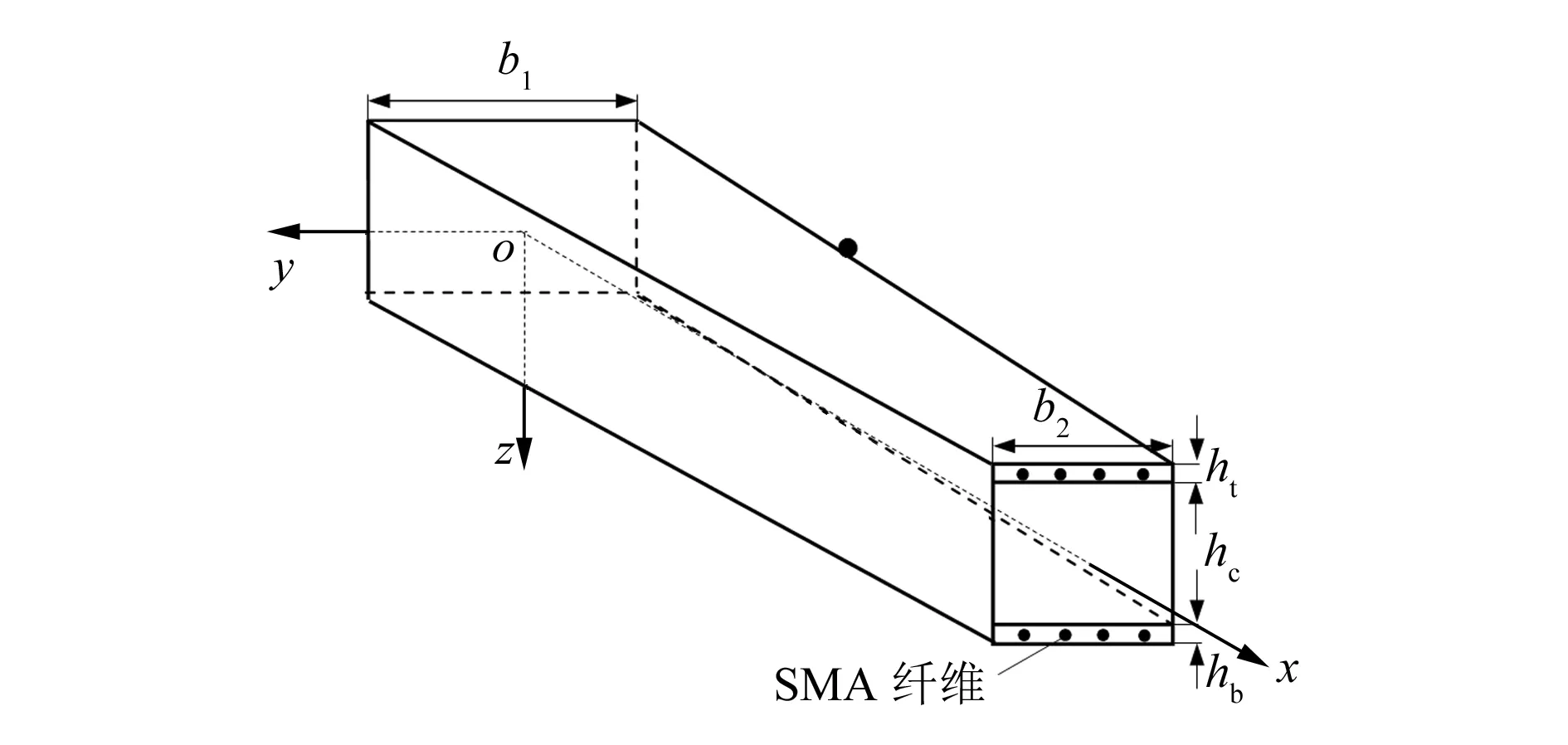
图1 SMA复合材料变截面结构
(1)
式中:u0和w0分别为层合梁中面沿x,z方向的位移。
层合梁中任意一点的线应变ε可表示为:
ε=ε0+zκ
(2)
式中:ε0为中面应变;κ为弯曲曲率。
当SMA复合材料结构发生中等挠度变形时,中面应变ε0可表示为:
(3)
SMA纤维的应力、应变与马氏体相变分数等状态变量之间的非线性关系采用Brinson[13]提出的一维唯象本构模型来描述。含SMA纤维的复合材料单层按照正交各向异性复合材料处理。
由于SMA的相变特性、材料非线性与复合材料结构变形的几何非线性相互耦合,因此利用有限元法研究该复合材料变截面结构的静力学响应。整体结构的静力平衡方程按照虚功原理建立,具体推导及求解方法见文献[14]。
若SMA复合材料变截面结构受轴向载荷作用,则只存在x方向的位移u,而y和z方向位移均为零。其理论分析与变截面结构受横向载荷作用时相似,此处不再赘述。
2 程序验证
本文用MATLAB语言编写了静态非线性有限元程序,用其来求解SMA复合材料变截面结构的非线性静力学响应。本节通过两个算例对所编写的MATLAB程序的可靠性和计算精度进行验证。
算例1, 普通纤维增强复合材料变截面结构。
将图1中的SMA纤维用普通纤维代替,该普通纤维的弹性模量为72 GPa,单层中的纤维体积含量为20%。层合结构中各单层的基体材料相同,弹性模量均为3 GPa。纤维及基体的泊松比均为0.28。该复合材料结构左端固定,右端自由,自由端作用有沿z轴正向的集中力F,F=40 kN。变截面结构的尺寸为:L=2 m,b1=0.3 m,b2=0.2 m,ht=hb=0.02 m,hc=0.16 m。
将该变截面结构沿长度划分为10个平面梁单元,并从固定端开始对节点连续编号1,2,3,…,11,则由本文MATLAB程序及商用软件ANSYS计算得到的各个节点的挠度如图2所示。为便于比较,图2中还给出了几何线性分析的结果。
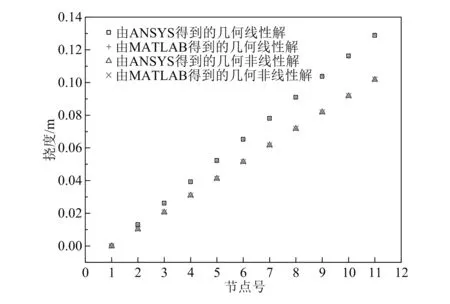
图2 普通纤维增强复合材料梁各节点的挠度
从图2中可以看出,几何非线性和几何线性两种情况下的MATLAB解与ANSYS解吻合得非常好。梁的挠度随节点号的增大而增大,自由端(节点11)处挠度最大。但是,几何非线性分析时各个节点的挠度比几何线性分析时的小。
算例2,内嵌SMA纤维的复合材料等截面结构。
令图1中b1=b2=b。SMA复合材料等截面结构尺寸为:L=2 m,b=0.3 m,ht=hb=0.02 m,hc=0.06 m。复合材料基体弹性模量为0.5 GPa,泊松比为0.28。SMA纤维的单层体积含量为40%,材料参数见表1[12]。其中,各材料参数的含义参见文献[12]。复合材料结构的约束方式同算例1,自由端作用有沿z轴正向的集中力F,F=80 kN。利用本文MATLAB程序及ANSYS软件计算考虑结构几何非线性时该SMA等截面梁加、卸载过程中自由端的挠度与载荷的关系,结果如图3所示。
由图3可以看出,由于SMA的伪弹效应,SMA复合材料等截面梁在加、卸载过程中自由端的挠度随载荷的变化曲线形成了封闭的滞后环,最大挠度约为0.32 m,MATLAB解与ANSYS解基本一致。

表1 SMA纤维的材料参数
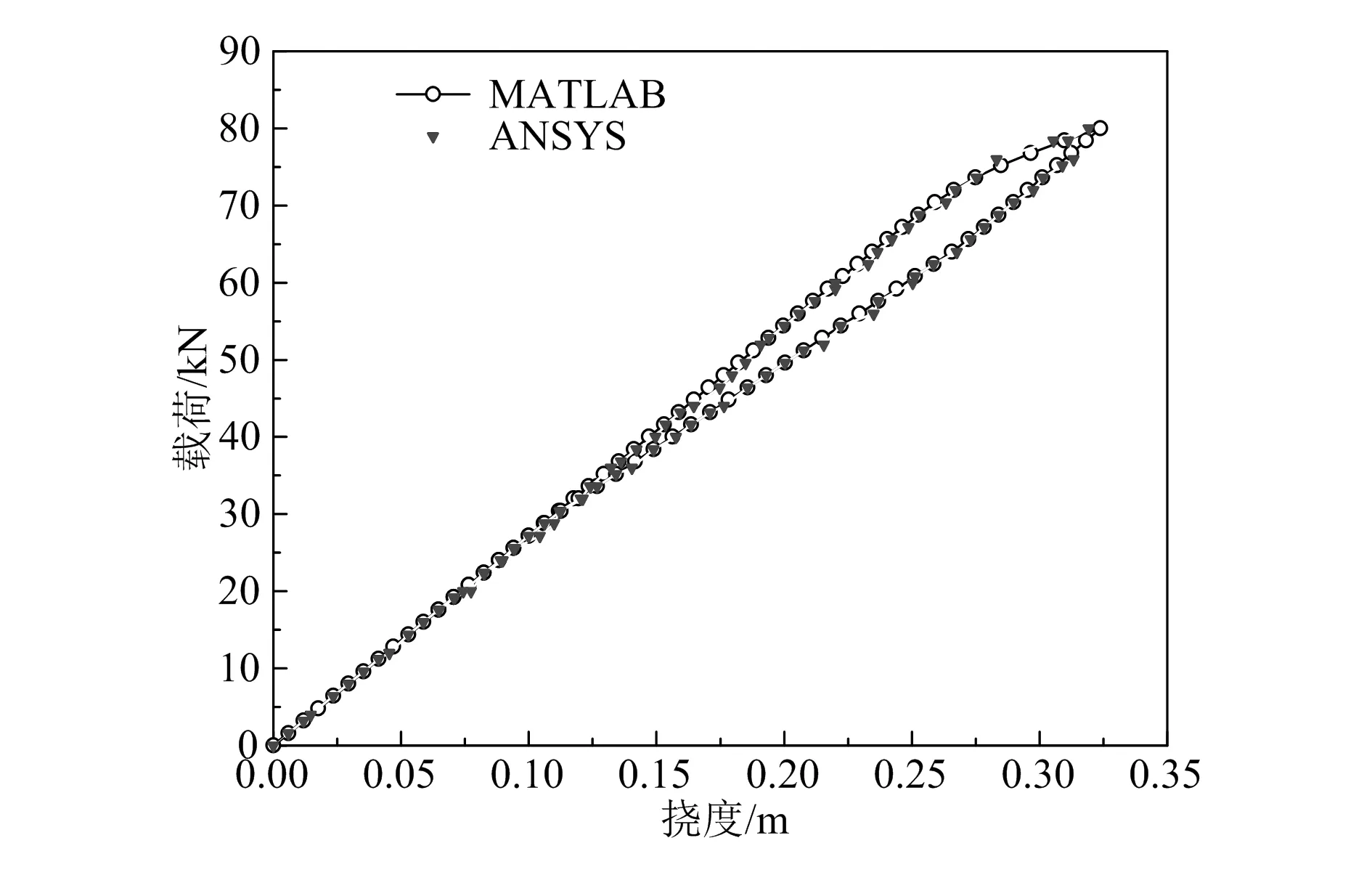
图3 SMA复合材料等截面梁自由端挠度随载荷的变化
上面两个算例均说明,本文利用MATLAB编写的非线性有限元程序是可靠的,具有较高的计算精度。
3 数值模拟与讨论
本节利用编写的非线性有限元程序对图1所示SMA复合材料变截面结构的静力学响应进行数值模拟。数值模拟时变截面结构的尺寸为:L=2 m,b1=0.3 m,b2=0.2 m。单层中SMA纤维的体积含量为40%,SMA的材料参数见表1。操作温度为20 ℃。SMA复合材料变截面结构的约束方式及基体材料同算例1。
3.1 SMA复合材料变截面结构受横向载荷作用时的静力学响应
变截面结构各层的厚度为:ht=hb=0.05 m,hc=0.10 m。自由端受沿z轴正向的集中力F作用,F=25 kN,则加、卸载过程中自由端的挠度随载荷的变化关系如图4所示。
从图4中可以看出,变截面梁加载时的自由端挠度-载荷曲线与卸载时的不重合,形成了封闭的伪弹性滞后环,说明内嵌SMA纤维的复合材料变截面结构具有耗能能力。但是由几何非线性分析得到的挠度-载荷滞后环面积比几何线性分析得到的要小。此外还发现,随着载荷的增大,几何非线性分析与几何线性分析结果的差异逐渐增大。当载荷达到最大值时,由前者得到的最大挠度约为0.20 m,但由后者得到的最大挠度约为0.24 m,即前者较后者减小约17%。因此,当弯曲变形较大时,应按照几何非线性理论预测SMA对变截面结构的变形抑制效果。

图4 SMA复合材料变截面梁自由端挠度随载荷的变化
图5给出了变截面梁弯曲时顶层和底层SMA纤维的应力-应变关系。由图5可以看出,变截面梁弯曲时顶层SMA纤维发生了相变,加、卸载过程中应力与应变曲线形成了明显的伪弹性滞后环;而底层SMA纤维没有发生相变,一直处于线弹性变形阶段。这可能是由于变截面梁弯曲时中性轴与形心轴不重合,中性轴较形心轴下移,导致顶层SMA纤维被拉伸的程度比较大,拉应力达到了发生马氏体相变所需要的临界应力而发生了马氏体相变;而底层SMA纤维被压缩的程度较小,压应力水平较低,没有达到马氏体相变所需要的临界应力,故没有发生马氏体相变。此外,从图5(a)还可以看出,由几何非线性分析得到的SMA伪弹性滞后环面积比几何线性分析时的小很多,这说明几何非线性分析时变截面梁顶层SMA纤维单位体积内耗散的能量较几何线性分析时的少。这也正是图4中几何非线性分析时SMA复合材料变截面梁挠度-载荷滞后环面积较小的原因。
为进一步分析变截面梁弯曲时SMA纤维的相变情况,本文给出了顶层和底层SMA纤维的马氏体体积含量与应变的关系,如图6所示。
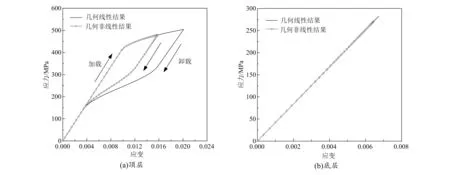
图5 变截面梁弯曲时SMA纤维的应力-应变关系

图6 变截面梁弯曲时SMA纤维的马氏体体积含量与应变的关系
从图6可以看出,加、卸载过程中顶层SMA纤维发生了马氏体正相变和逆相变,由几何线性分析得到的最大马氏体含量约为0.11,而几何非线性分析得到的约为0.06,比前者低了近50%。但是底层的SMA纤维因为没有发生相变,所以马氏体含量一直为零。
3.2 SMA复合材料变截面结构受轴向载荷作用时的静力学响应
复合材料变截面结构各层的厚度为:ht=hb=0.02 m,hc=0.16 m。自由端受拉伸载荷F作用,F=30×103kN,则加、卸载过程中自由端的纵向位移与载荷的关系如图7所示。
从图7可以看出,SMA复合材料变截面结构在加载和卸载过程中纵向位移随载荷的变化形成了封闭的滞后环,说明变截面结构在拉伸加、卸载过程中耗散了一定的能量。但是由几何非线性分析得到的滞后环面积明显小于几何线性分析时的面积。相同载荷水平下,由几何非线性分析得到的纵向位移比几何线性分析时的小,而且载荷越大,二者的差值越大。以变截面结构达到最大载荷为例,由几何非线性分析得到的最大纵向位移约为0.10 m,而由几何线性分析得到的最大纵向位移约为0.16 m,前者较后者降低了约38%。这是由于考虑结构几何非线性时预测的SMA纤维的伪弹耗能能力及相变程度较未考虑时均降低的缘故,具体可见图8和图9。
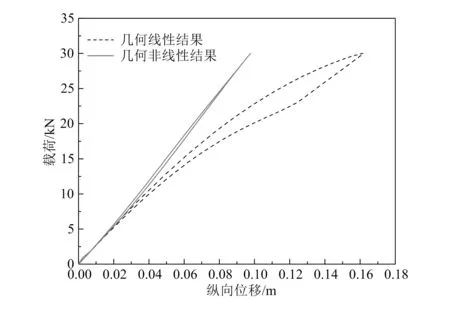
图7 变截面结构拉伸时自由端纵向位移与载荷的关系
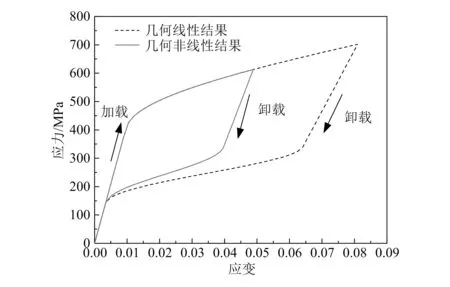
图8 变截面结构拉伸时SMA纤维的应力-应变曲线
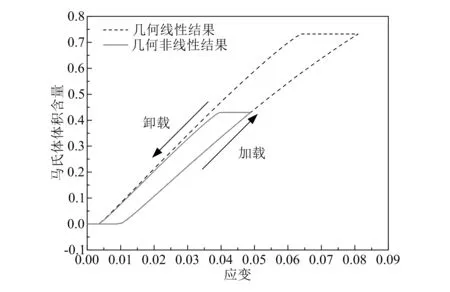
图9 变截面结构拉伸时SMA纤维马氏体体积含量与应变的关系
图8是变截面结构拉伸时SMA纤维的应力-应变曲线。由图8可以看出,拉伸加、卸载过程中内嵌在变截面结构中的SMA纤维应力与应变形成了明显的伪弹性滞后环。但是几何非线性分析得到的滞后环面积明显小于几何线性分析的结果。
变截面结构在拉伸加、卸载过程中SMA纤维的马氏体体积含量与应变的关系如图9所示。从图9可以看出,加载过程中,当应变较小时SMA的马氏体含量一直保持为零,即没有发生马氏体正相变。当应变约大于0.01以后,SMA逐渐发生了奥氏体向马氏体的转变,且马氏体含量随着应变的增大逐渐增大。由几何非线性分析得到的最大马氏体含量约为0.43,而几何线性分析得到的约为0.73,前者较后者减少了41%。卸载时马氏体含量先保持不变,然后随着应变的降低而逐渐降低,即发生了马氏体逆相变。当卸载结束时马氏体含量降为零。
4 结论
本文在考虑结构几何非线性的基础上研究了内嵌伪弹性SMA纤维的复合材料变截面结构加、卸载过程中的静力学响应规律,得到的主要结论如下:
1)无论沿横向还是轴向加、卸载,SMA复合材料变截面结构加载时的位移-载荷曲线与卸载时的不重合,加卸载曲线形成了封闭的滞后环。相同载荷水平下,由几何非线性分析得到的位移量比由几何线性分析得到的小,且二者的差值随着载荷的增大而增大。
2)当SMA复合材料变截面结构受横向载荷作用时,因形心轴上下两侧变形不对称,一侧的SMA纤维发生了马氏体正相变和逆相变,起到了伪弹耗能作用;而另一侧的SMA纤维加、卸载过程中均未发生相变,未起到耗能作用。
无论沿横向还是轴向加、卸载,由几何非线性分析得到的变截面结构中SMA纤维的应力-应变伪弹性滞后环面积、最大马氏体含量均比几何线性分析的结果小很多。
本文的研究可为SMA在大型风力机复合材料叶片智能化控制及大变形结构被动控制中的应用提供一定的理论指导。

