高重合度内啮合摆线齿轮副机构设计与建模分析
雷艳惠,贾芳云
(咸阳职业技术学院机电学院,陕西 咸阳 712000)
现代工业中最常用的机械传动为齿轮传动,齿轮传动中应用最广的是行星齿轮传动[1]。行星齿轮传动中较为常用的是内啮合齿轮传动,其结构尺寸较小,使用时具有滑动系数低、接触应力小、弯曲强度高、使用寿命长、传动效率高且承载能力高等优点[2-3],可实现动力传动装置的高速、高效、重载、结构小及运转平稳等要求[4-6]。内啮合齿轮副由一个内齿轮和一个外齿轮组成,可实现定轴与行星传动[7-8]。由于内啮合齿轮传动的重合度是决定齿轮强度高低的首要影响条件,是决定齿轮传动连贯性的首要因素,因此提升重合度是提高行星齿轮传动效率与承载能力、降低振动与噪声的首要措施[9-10]。
为降低行星齿轮的振动与噪声,提升其重合度,本文设计了一种具有高重合度的新型内啮合复合摆线齿轮副,其在一定程度上有助于实现内啮合齿轮传动的高重合度,并提高减速机的承载能力。
1 高重合度内啮合摆线齿轮副机构设计
1.1 共轭齿廓方程
内啮合摆线齿轮内外齿轮传动时的接触点轨迹如图1所示。
以图1中节点G为原点,作固定坐标系Oxy,其中x轴与O1O2垂直,y轴与其重叠,那么啮出时啮合线方程为:
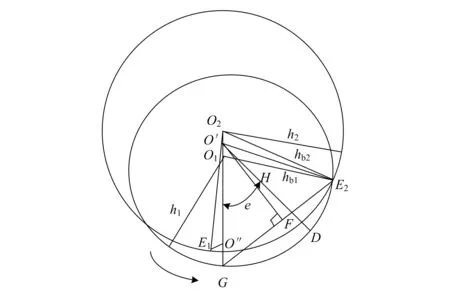
图1 内啮合摆线齿轮传动接触点的轨迹
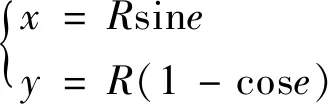
(1)
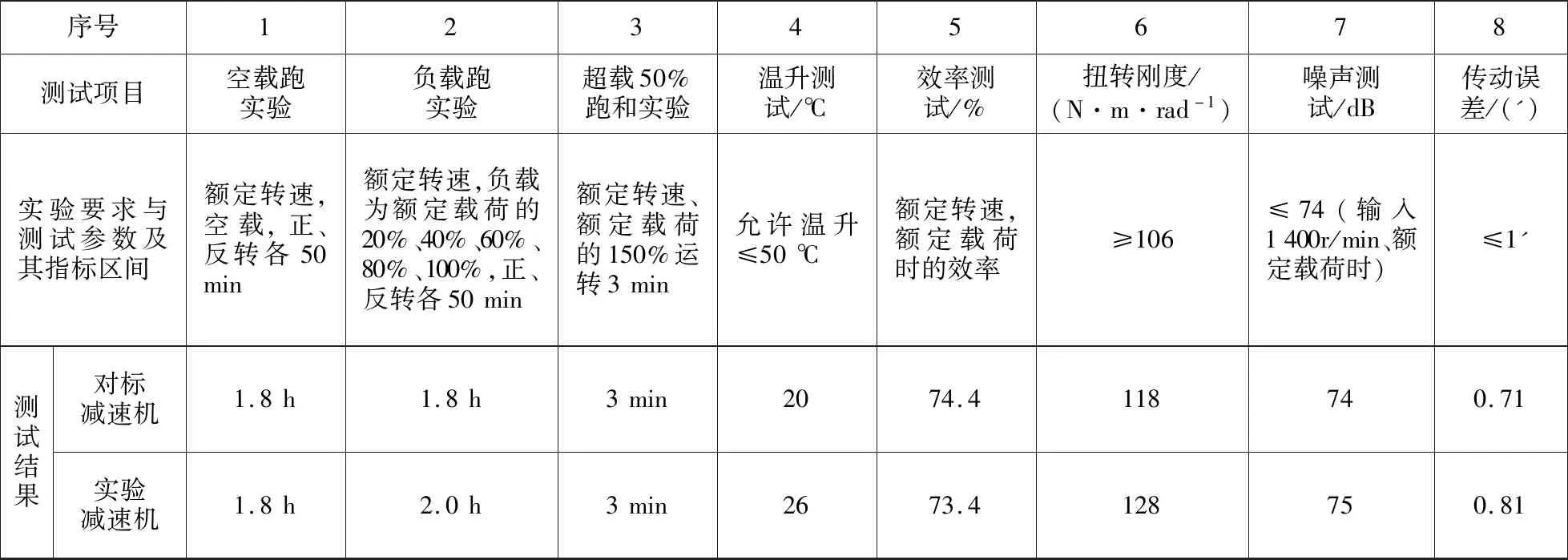
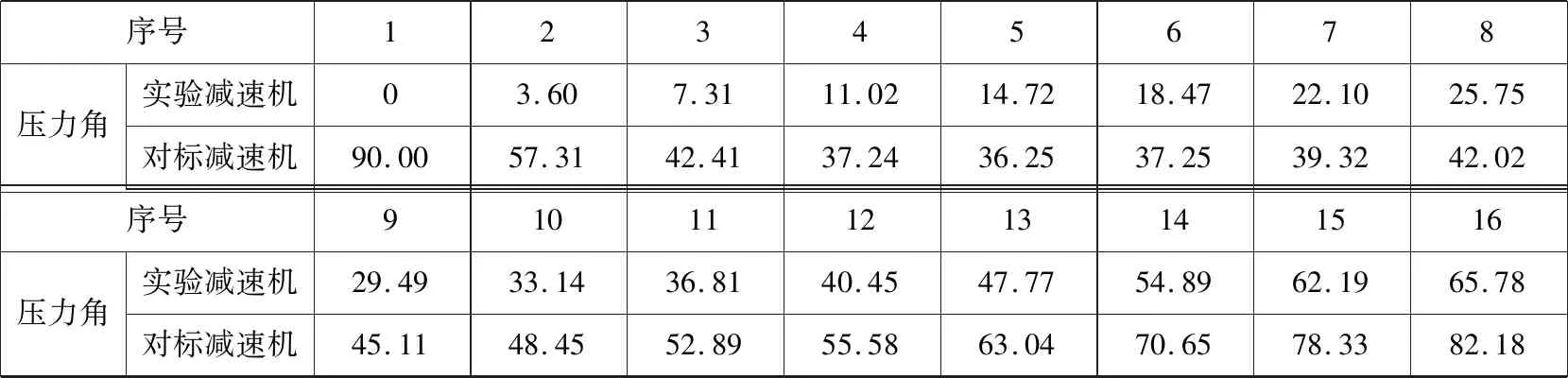
式中:x和y为两个齿轮啮出时啮合线横、纵坐标;R为啮出时啮合线的变化量;e为啮合线上动点D的轨迹半径O′D与O′G的夹角,即半径O′G以逆时针方向转动时的角度。假设齿轮终止时转角为e2,那么0 通过分析齿轮啮合原理可知[11],外齿轮1与内齿轮2的齿廓为啮合线各接触点在外齿轮1与内齿轮2转动时平面上的轨迹,设置外齿轮1的中心O1为原点的坐标系O1x1y1,坐标系与O1相连且共同旋转,x1轴的最初位置和O1O2垂直,y1轴与O1O2重合,如此可求出外齿轮1的齿顶位置包心外摆线齿廓方程,表达式为: (2) 式中:xb1和yb1分别为外齿轮1的外摆线齿廓的横、纵坐标;H为外齿轮1齿顶位置变化量;h1为外齿轮1的半径。 设置以内齿轮2的中心O2为原点的坐标系O2x2y2,使坐标系与O2相连且共同旋转,x2轴的最初位置和O1O2垂直,y2轴和O1O2重合,由此可以得到内齿轮2的齿顶位置包心外摆线齿廓方程,表达式为: (3) 式中:xb2和yb2分别为内齿轮2的包心外摆线横纵坐标;h2为内齿轮2的半径。 同理,当啮合线啮入时的表达式为: (4) 其中,当半径O″G以顺时针方向转动时,其转角以参变量e表达,假如将齿轮初始啮合点参变量设为e1,那么0≤e≤e1。可得出当外齿轮1齿根位置滚圆半径是(h2-H)时,其无包心内摆线齿廓方程为: (5) 式中:xk1和yk1分别为外齿轮1的无包心内摆线横、纵坐标。 当处于极限条件下的内齿轮2齿根位置滚圆半径为(H-h1)时,其无包心外摆线齿廓方程为: (6) 式中:xk2和yk2分别为内齿轮2的无包心外摆线横、纵坐标。 由前述可知,为防止干扰,内齿轮2的无包心外摆线滚圆半径H′应大于极限半径(H-h1),即H′>(H-h1)。 然而,内齿轮2齿根位置的齿廓不仅局限于此外摆线齿廓,还包括可以在啮合时期内不产生干扰,且可提供充分弯曲强度的任意曲线齿廓[12]。 通过式(1)算得对应的齿条齿廓方程是: (7) 式中:X和Y分别为齿廓的横、纵坐标;y′(e)为廓隙系数;y(e)为廓宽系数;A为积分常数。 为求出式(7)中的积分常数A,在初始位置取齿条齿廓经过G点,即当e=0时,X和Y均等于0,因此齿条齿廓方程为: (8) 进而得出啮出时齿轮的作用角φb为: (9) (10) 在ΔO1O2E2中,通过半角定理可以得出: (11) 式中:g=(b+c+d)/2。由此可得: (12) 在ΔO1GE2中,通过余弦定理可以得出: (13) (14) 因此: (15) (16) 通过重合度统一定义,可得出内啮合摆线齿轮副的最高重合度εmax: (17) 式中:μ为啮合过程中齿轮作用角;μf和μb分别为啮入期间齿轮转角和啮出期间齿轮转角;δ=2π/m。 (18) 由于2(h2-H)≤h1,因此在外齿轮1与内齿轮2的齿数z1和z2固定时,z1不可过小,z2不可过大,即传动比或齿数差(z2-z1)不可过大。设计过程中,需按此校对,传动比区间为1 1.3.1节圆上齿廓的设计 节圆半径可由式(19)计算: (19) 式中:O1,O2为两节圆的圆心坐标值。在h1>h>h2的前提下,以圆弧为啮合线,h为啮合线半径,O为其圆心。G是啮合线h上的一点,起始时两个圆在此点相切。 保持O1,O2不动,将啮合圆O围绕两者滚动,得出G点的内摆线与内切外摆线分别为G1,G2。内外齿轮的节圆上齿廓分别设为G1,G2,那么二者均可达到共轭关系[13]。 创建直角坐标系,得出啮合圆O的方程: (20) 其中半径OG的逆时针转角以e表示。 根据以上啮合原理,可得两齿轮节圆上齿廓的方程: (21) (22) 当z1=45、z2=37、m=5时,根据以上原理设计能够得到节圆上齿廓啮合状态的部分状况。 1.3.2节圆下齿廓的设计 由于齿根位置未参加啮合,因此在设计时可以从加工工艺、润滑及强度等方面统一考量[14]。为使齿根进行二次啮合接触,利用节圆下齿廓能够通过摆线的特点,设计出内齿轮2齿根位置同外齿轮1齿顶位置共轭的内摆线[15]。 (23) 式中:γ为啮合角;γb1,γb2分别为齿轮1与齿轮2的齿顶压力角。本文通过“方程式驱动曲线”工具在SolidWorks内构建内外齿轮三维实体模型,再通过静态接触有限元分析软件ANSYS Workbench内的pds模块,从而检验高重合度内啮合摆线齿轮副机构传动计算的准确性及其原理的精准性。分析时,定义的接触面与目标面分别为内外齿轮共同啮合轮齿对的接触面,其接触约束条件为: χ≥2.013 3(z1-z2) (24) 式中:χ为转动副转矩。根据式(24)控制接触刚度,可在内齿轮的外表层实现约束。与此同时,采用本文方法制作一套同等尺寸的啮合摆线齿轮副机构,并用光弹实验测试齿轮静态啮合齿轮受力。由于摆线齿廓是较为复杂的几何形状,因此选取相关企业的加工中心来试验。齿轮机构在数控机床粗加工后,使用成型砂轮在数控磨床上磨削,从而确保达到精准度需求。传动过程中,齿轮副啮合部分的周期性改变是跟随偏心轴的转动而发生的,因此为实现各部分的啮合传动与载荷传递,需通过套筒对偏心轴与外齿轮分别给予反作用力矩。但是实验过程中难免产生误差,在较小的给予力矩作用下,无法达到理论齿数的啮合;为达到理论齿数的啮合,需施加一定的力矩载荷来消除啮合间隙。实验中的新型内啮合摆线齿轮副机构如图2所示,有限元仿真分析结果、光弹实验测试状况分别如图3、图4所示。 图2 新型内啮合摆线齿轮副机构 图3 有限元仿真分析结果 图4 光弹实验加载测试状况 由图3、图4可以看出,用本文方法设计的齿轮副实现了内啮合齿轮传动的高重合度。 工业机器人关节的关键组成部分为RV减速机,常见的传动方式为摆线针轮传动与外齿轮传动,其中摆线针轮传动与本文齿轮副传动具有同等精准度,可被本文齿轮副传动替代。实验的对标减速机选取凯力拓科技有限公司生产的RAS-60,以2.1节光弹实验构建的样机作为本文样机,该样机采用本文设计的摆线齿轮代替减速机中的针齿、摆线轮及齿圈,在准确安装、其余部位不改变且偏心距是1.3的前提下,变动齿轮的齿数和齿轮类型,将39齿的摆线轮、40针齿数的原传动参数,改变成齿数分别为49和50,半径为2.6 mm,且具有0.01 mm齿侧间隙。在实验RV减速机内安装本文设计的样机如图5所示,测试实验台如图6所示,测试结果见表1。 图5 RV减速机内的传动样机 图6 测试实验台 表1 两台减速机的检测参数及测试结果 由实验测试结果可知,安装本文设计的内啮合摆线齿轮副机构的实验减速机性能达到指标要求,与对标减速机性能几乎相等。由构件受力与运动方向组成的锐角为压力角,由于实验减速机共同参加啮合的齿数较多且压力角较小,故其对齿轮及偏心轴的受力状况有明显改进效果。摆线轮节圆与针轮节圆在摆线轮和针齿组啮合传动的刹那在G点相切。通过分析共轭啮合关系可知,摆线齿啮合及针齿G1~G8的公法线均经过G点,可见各啮合点位置的公法线GG1~GG8具有不同长度,故齿廓线每个点的压力角不固定。由此可知实验减速机的压力角同样不固定,根据结构参数,依据定义可算出两种减速机的压力角,见表2。 通过表2可知,实验减速机和对标减速机相比,各压力角明显减小,说明采用本文设计的内啮合摆线齿轮副机构的减速机能够提高齿轮的承载能力。 表2 两种减速机压力角的计算结果 (°) 本文设计的高重合度内啮合摆线齿轮副通用性强,为实现内啮合齿轮传动的高重合度提供了一定的技术支持,为提高减速机的承载力提供了一种新的解决方法。但是,目前的研究工作仅通过较为简单的实例来验证所设计方法的可行性,要真正在实践中体现其价值,还需要进行后续数据的处理以及进一步完善对复杂数据模型的支持,更大范围地验证该齿轮副机构在指导实际生产应用中的价值。
1.2 内啮合摆线齿轮副的重合度

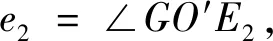
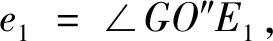
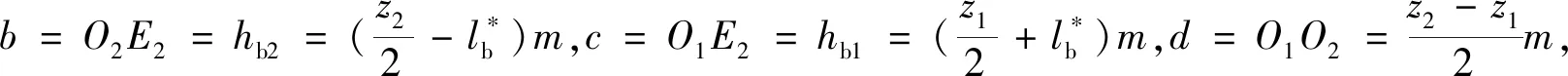
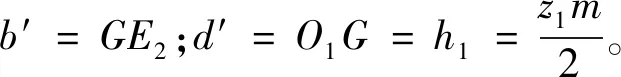
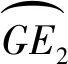
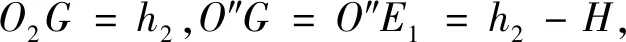
1.3 高重合度内啮合摆线齿轮副机构设计
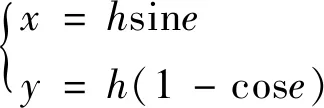
2 实验验证
2.1 光弹实验




2.2 样机实验


3 结束语

