基于虚拟环境的汽车圆柱齿轮精加工过程可靠性评估方法
杨 萌
(陕西国防工业职业技术学院,陕西 西安 710300)
随着机械精加工技术的快速发展,人们对汽车圆柱齿轮精加工过程的可靠性提出了更高的要求。对汽车圆柱齿轮精加工过程进行评估和加工精度寻优,能够提高汽车圆柱齿轮的加工精度,因此汽车圆柱齿轮精加工过程评估方法受到人们的广泛重视[1]。目前已有相关学者对汽车圆柱齿轮精加工过程评估方法进行了研究,并取得了一定的研究成果[2]。文献[3]提出一种基于切削稳定性约束下的汽车圆柱齿轮精加工铣削参数优化方法,通过设置机床、工件毛坯和刀具参数,引入模糊控制方法,对汽车圆柱齿轮精加工过程中的铣削参数进行控制,从而达到优化参数的目的,然而该方法在加工过程中各分目标权重的自适应配置较差,导致加工误差较大;文献[4]将蒙特卡罗随机有限元方法(MCSFEM)与应力-强度干涉理论相结合,提出一种新的可靠性评估方法,采用随机有限元法分析研究对象的疲劳接触应力分布,在此基础上,利用应力-强度干涉理论实现了评估研究,然而该方法的研究结果误差较大。
针对上述问题,本文提出基于虚拟环境的汽车圆柱齿轮精加工过程可靠性评估方法。通过构建齿轮刀齿运动调控函数、分析动态扰动特征、采用颤振稳定域及表面位置误差调节方法,优化汽车圆柱齿轮精加工的切削参数,提取加工过程可靠性评估的状态参量,使加工状态参量误差达到收敛的目的,并采用虚拟视景仿真技术,实现汽车圆柱齿轮精加工过程可靠性评估。
1 汽车圆柱齿轮加工表面稳定性调控及优化
1.1 齿轮刀齿运动调控函数构建
为了实现汽车圆柱齿轮精加工过程可靠性评估,需要构建汽车圆柱齿轮精加工工件表面稳定性控制参数辨识模型;结合参数模型的优化识别,控制参数动态变化,以提高加工过程的可靠性。分析主轴-切削交互过程,确定汽车圆柱齿轮精加工时刀具运行产生的轨迹,进行汽车圆柱齿轮精加工的构件表面几何建模[5]。以1M-20Z型圆柱齿轮作为研究对象,其模数为1 mm,齿数为20,齿高为32 mm,齿宽为3 mm,建立的圆柱齿轮模型如图1所示。
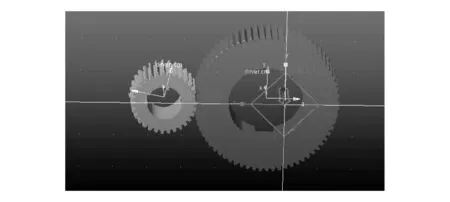
图1 圆柱齿轮模型
局部干涉和全局干涉约束下汽车圆柱齿轮精加工工件表面稳定性控制参数辨识模型为:
(1)
式中:x1(t)和x2(t)分别为不同轨迹点条件下圆柱齿轮精加工稳定性控制函数;将x0设置为坐标原点,fx1(x1-x0)和fx2(x2-x0)分别为刀具运行产生的轨迹点f在坐标点x1和x2下的控制参量;gx1(x1-x0)和gx2(x2-x0)分别为刀具运行产生的轨迹点g在坐标点x1和x2下的控制参量;t为精加工圆柱齿轮所用时长。
考虑待加工曲面上所有特征点的辨识误差,构建一个(2+1)维GIR方程对汽车圆柱齿轮精加工时工件的惯性进行约束参量调节,得到汽车圆柱齿轮加工过程的可靠性调节系数矩阵A,记作:
(2)
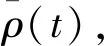
(3)
结合不同加工状态下的稳定域[0,Φ]进行汽车圆柱齿轮精加工工件表面参数调节,令:
(4)
式中:Φ为稳定域边界特征量。
在优化切削参数的条件下,对切削角度θp进行自适应寻优,在进给方向和法向激励方向上,选取sinθp∈(0,θp),cosθp=(θp,1),在小角度范围内,得到汽车圆柱齿轮精加工的齿轮数值测量结果。
根据汽车圆柱齿轮精加工的优化参数,对齿轮数值测量结果进行模糊控制[7]。在二维Bernoulli空间中,汽车圆柱齿轮精加工刀齿运动调控函数可以描述为:
(5)
1.2 动态扰动特征分析
汽车圆柱齿轮精加工过程中,刀齿的振动会造成动态扰动,从而影响齿轮的加工稳定性。分析由刀齿的振动引起的动态扰动因素[8],考虑汽车圆柱齿轮工件表面的间歇进给误差,得到动态扰动数据点分布,描述为:
V1(m(t))=2mT(t)Am(t)+2mT(t)τm(t)-(1-τ)mT(t)Q2m(t)+mT(t)Q1
(6)
V2(m(t))=mT(t)(Q1+Q2)m(t)-mT(t-τ)Q1m(t-τ)
(7)
V3(m(t))=mT(t)(h1Q1+h2Q2)m(t)-
Q2m(t-h1)
(8)
式中:V1(m(t)),V2(m(t))和V3(m(t))为不同的动态扰动数据点;m为间歇进给误差矩阵;m(t)为误差动态扰动量;τ为刀齿的振动调节系数;Q1和Q2为刀齿振动量;h1和h2为刀齿的振动频率。
采用误差反馈调节方法进行颤振稳定域及表面位置误差调节,在主轴功率及加工稳定性等约束条件下,定义汽车圆柱齿轮精加工的主轴随动坐标系OjXjYjZj,将所有刀齿上的切削力相加,得到汽车圆柱齿轮精加工过程动态扰动特征量λ(特征根),λ决定了汽车圆柱齿轮精加工的刀具姿态,则在坐标轴OjXj上,通过第j个轴向切削的特征量,求解汽车圆柱齿轮精加工的稳态方程为:
λ2+j[V1(m(t))+V2(m(t))+V3(m(t))]=0
(9)
在多工艺参数组优化问题的解耦约束下,进行动态扰动特征控制,得到动态扰动特征量为:
(10)
式中:ρi为解耦预测函数。
当导引进给在Y轴方向时,分析由于刀齿的振动引起的动态扰动因素,结合动态扰动特征分析结果,可完成对汽车圆柱齿轮加工表面稳定性的调控及优化。
2 加工过程可靠性评估
2.1 加工状态参量误差收敛分析
根据得到的动态扰动特征量,结合汽车圆柱齿轮精加工刀齿运动调控函数调节动态扰动,达到加工误差的收敛控制。在汽车圆柱齿轮精加工过程中进行工件表面稳定性调控,以工件特征gk、工序安排Ak等为控制约束对象,根据切削加工中刀齿的位置进行汽车圆柱齿轮精加工的误差反馈调节[9-10],分析横向残余应力,在边界值稳定的条件下进行汽车圆柱齿轮精加工的自适应反馈调节,分析走刀路径对残余应力分布的影响。
令D(s),G(t)为加工过程可靠性评估的状态分布参量,计算刚度条件下平衡约束函数J:
(11)
采用共轭梯度法进行汽车圆柱齿轮精加工的奇异分解,在汽车圆柱齿轮精加工的进刀轨迹曲线中,得到最优解的进化方程:
gk+AkJ=0
(12)
以工件特征gk、工序安排Ak等为控制约束对象,得到模糊控制函数Hk为:
(13)
式中:μk为汽车圆柱齿轮待加工曲面曲率。
结合临界元素跟踪控制方法,实现汽车圆柱齿轮精加工的联动控制优化,得到状态参量的误差收敛值S为:
S=(J+μkIT)2+JHk
(14)
式中:I为误差收敛矩阵。
根据状态参量的误差收敛值S,结合临界刀轴矢量特征分布,可得可靠性输出评估。
2.2 基于虚拟环境的汽车圆柱齿轮精加工过程可靠性评估
以工件特征gk、工序安排Ak等为控制约束对象,结合虚拟环境仿真技术实现汽车圆柱齿轮精加工过程可靠性评估,计算汽车圆柱齿轮待加工曲面曲率函数f(X)的多目标优化解,得到临界刀轴矢量特征分布W′:
(15)
在进行复杂曲面通道多轴加工时,需求解汽车圆柱齿轮精加工的最优参数,当模糊约束参量H满足H∈W′时,汽车圆柱齿轮精加工的过程传递函数Y(s)表述为:
(16)
将刀轴可行摆刀域进行联合参量评估,在虚拟环境下,存在刀轴的摆动干扰误差,结合复杂曲面通道的误差反馈调节结果进行汽车圆柱齿轮精加工的刀轴自动修正,修正函数F(x)为:
(17)
假设fi(xi,θi)为汽车圆柱齿轮精加工中时滞向量θi(i=1,2,…,n)的可靠性界定分布函数,则汽车圆柱齿轮精加工过程的可靠性评估输出Z为:
Z=fi(xi,θi)+F(x)
(18)
3 仿真实验与结果分析
为验证本文方法在实现汽车圆柱齿轮精加工过程中可靠性评估的应用性能,进行仿真测试分析。在VERICUT软件中搭建齿轮加工的虚拟环境,测试加工对象为1M-20Z型汽车用齿轮,应用本文方法测试加工1 000个齿轮过程中的动态扰动量,并采用文献[3]、文献[4]方法为实验对照组,得到的对比结果如图2所示。
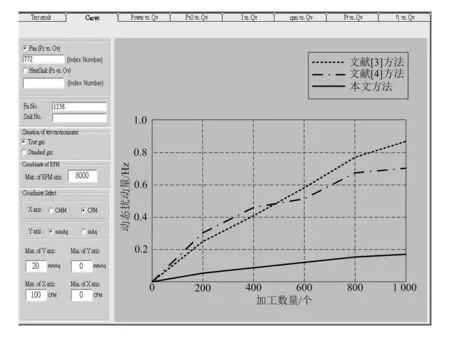
图2 汽车圆柱齿轮精加工过程动态扰动量对比
动态扰动量即为齿轮加工过程中的刀齿振动频率。分析图2可知,在1 000个圆柱齿轮加工过程中,文献[3]方法的动态扰动量为0.85 Hz,文献[4]方法的动态扰动量为0.70 Hz,而本文方法的动态扰动量为0.18 Hz,远远小于文献[3]、[4]方法。实验结果表明,本文方法能够有效控制齿轮加工过程中的动态扰动量,齿轮加工的稳定性更好。
在此基础上,分析3种方法的误差收敛控制情况,得到对比结果如图3所示。
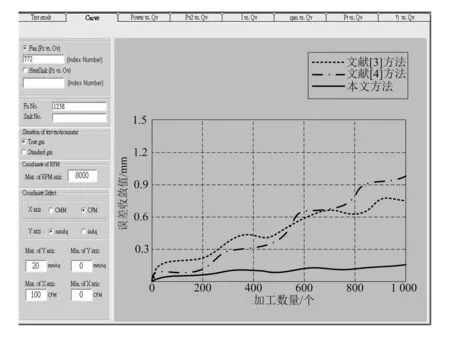
图3 汽车圆柱齿轮精加工过程误差收敛控制情况对比
分析图3可知,在齿轮加工过程中,随着加工数量的增加,误差收敛值也不断增加。文献[3]方法的误差收敛值为0.75 mm,文献[4]方法的误差收敛值为1.00 mm,而本文方法的误差收敛值为0.15 mm。由此可见本文方法的误差收敛值较小,误差收敛控制较好。
根据上述对动态扰动量及误差收敛控制参数的评估结果,对比本文方法、文献[3]和文献[4]方法的加工误差,结果如图4所示。
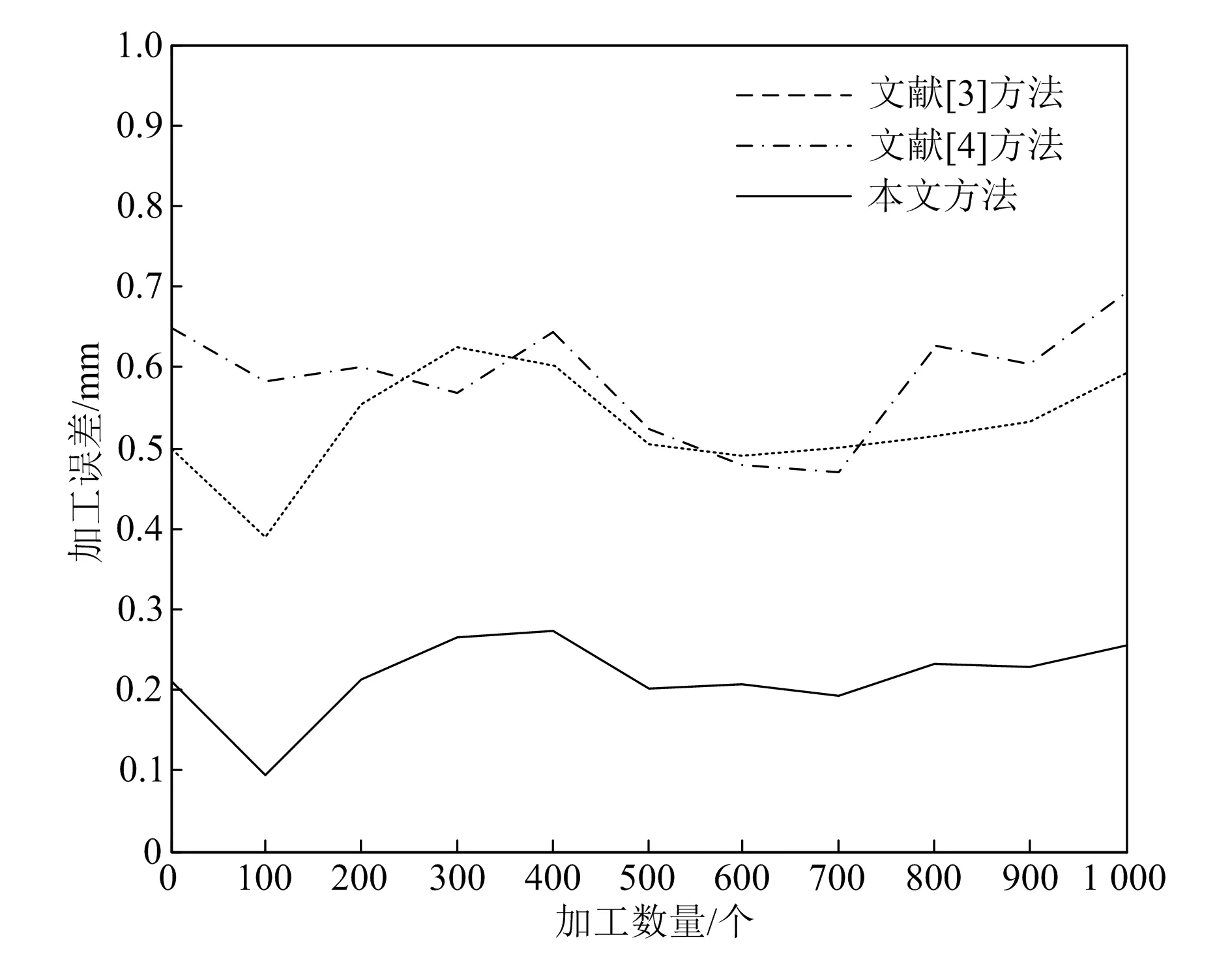
图4 加工误差测试结果
分析图4可知,采用本文方法进行汽车圆柱齿轮精加工过程可靠性评估,加工误差较小,不超过0.3 mm,平均误差在0.2 mm左右,文献[3]、文献[4]方法的平均误差均在0.6 mm左右。由此可看出本文方法具有一定的优势,加工误差小,能够准确完成对汽车圆柱齿轮精加工过程的可靠性评估。
4 结束语
本文提出了基于虚拟环境的汽车圆柱齿轮精加工过程可靠性评估方法,通过构建控制参数辨识模型与齿轮刀齿运动调控函数,分析刀齿振动引起的动态扰动因素,优化汽车圆柱齿轮加工表面稳定性。通过提取加工过程可靠性评估的状态参量,得到状态参量的误差收敛值。以工件特征、工序安排等为控制约束对象,结合虚拟视景仿真技术,完成汽车圆柱齿轮精加工过程可靠性评估。实验结果表明,采用该方法进行汽车圆柱齿轮精加工过程评估的可靠性较好,降低了加工误差,提高了加工精度。

