非正弦激励下铁心损耗计算模型改进*
杨守君, 赫荣臻,, 张艳丽, 张殿海, 唐 伟, 杨朝晖, 刘 圳
(1. 中车大连机车车辆有限公司 技术中心, 辽宁 大连 116300; 2. 沈阳工业大学 电气工程学院, 沈阳 110870)
中、高频非正弦激励会使电力电子变压器铁心损耗迅速增加,影响电力电子变压器整体运行效率[1-2].中、高频变压器通常采用的铁心材料有软磁铁氧体、非晶合金或纳米晶;激励形式包括方波、三角波或PWM波等非正弦激励形式.目前,铁心制造商通常会提供正弦激励下铁心磁特性和损耗数据,传统损耗计算经验公式仅适用于正弦激励的情况,已不能满足中、高频变压器铁心损耗计算要求[3-4].
铁心损耗计算的常用方法有:基于铁心磁化物理现象建立的磁滞模型法、Steinmetz经验公式法、Bertotti损耗分离模型等.其中,用于铁心损耗计算的磁滞模型常采用Jiles-Atherton模型和Stoner-Wahlfarth模型,尽管这些模型建立在一定的磁化机理上,但模型参数多,与有限元数值计算结合过程复杂,较难应用到工程实践中[5-6].Steinmetz损耗公式利用频率与磁通密度计算损耗体密度,是一种单纯的数学表述,因公式简单、参数少被广泛应用在工程设计中[7].近些年,用于方波和矩形波激励的各种Steinmetz修正模型被提出,模型的准确性和适用性也被学者们深入讨论[8-9],为非正弦激励下的铁耗计算提供了参考.非正弦激励下Bertotti损耗计算采用的方法是将非正弦激励等效为不同频率正弦信号的叠加,再将各正弦信号引起的铁心损耗进行线性叠加[10].在此基础上,文献[11]对磁滞损耗系数和涡流损耗系数进行改进,计算了铁心在PWM波激励下的损耗.叠加原理在数学上仅适用于线性系统,而铁心材料的损耗与磁通密度之间存在非线性关系,模型的应用必然会引起较大的误差.
为了更为准确地预估非正弦激励下铁心损耗,本文首先测量软磁铁氧体和纳米晶两种环形铁心在正弦波、方波和PWM波下的损耗.在此基础上,对Bertotti损耗分离模型的异常损耗计算公式进行修正,分析Barbisio算法求取异常损耗系数的局限性,给出系数与频率和磁通密度的关系函数,进一步细化了Bertotti损耗分离模型中涡流损耗公式,使其适用于矩形截面铁氧体的涡流计算.
1 非正弦激励下环形铁心损耗测量
在改进实验室现有的磁特性测量系统基础上[12],搭建了如图1所示的非正弦激励下环形铁心损耗测量系统.该测量系统包括数据采集卡、功率放大器、隔离放大器、上位机等几部分.其中,数据采集卡将上位机中LabView软件生成的激励波形传送到功率放大器,经信号放大后施加到环形铁心的励磁绕组中.同时,采集取样电阻和二次侧绕组两端电压反馈到上位机,再利用安培定律和电磁感应定律计算铁心中磁通密度和磁场强度波形,铁心损耗可计算为
(1)
式中:ρv为铁心密度;T为励磁周期;B为磁通密度;H为磁场强度.被测铁心环样为软磁铁氧体、纳米晶环形铁心.

图1 非正弦激励下铁心损耗测量系统示意图Fig.1 Schematic diagram of core loss measurement system under non-sinusoidal excitation
图2给出了软磁铁氧体和纳米晶在不同频率下的损耗曲线,由图2结果可知,在同样频率下纳米晶的铁心损耗都远小于软磁铁氧体铁心损耗.
2 Bertotti损耗分离模型改进与验证
Bertotti损耗分离模型将铁心损耗表达为磁滞损耗Wh、涡流损耗Wed和异常损耗Wex之和的形式,即
W=Wh+Wed+Wex
(2)
其中,通常用准静态磁滞回线的面积代表磁滞损耗的大小,而涡流损耗的大小与材料的叠片形式相关.计算叠片铁心的涡流损耗[12]及圆形截面实心铁磁材料的涡流损耗[13]的表达式分别为
(3)
(4)
式中:d为叠片厚度;σ为材料电导率;S为横截面积.电力电子变压器软磁铁氧体铁心的截面通常为矩形,制作工艺简单方便,成本低.
异常损耗与磁化速率密切相关,不同激励方式异常损耗表达式为
(5)
式中:G为无量纲常数,通常取为0.137 5;V0为待定系数,其确定方法决定了异常损耗计算的准确性.
2.1 软磁铁氧体矩形截面铁心涡流损耗计算
图3给出了矩形截面的磁通密度方向与涡流路径.由电磁感应定律可知,涡流损耗可计算为
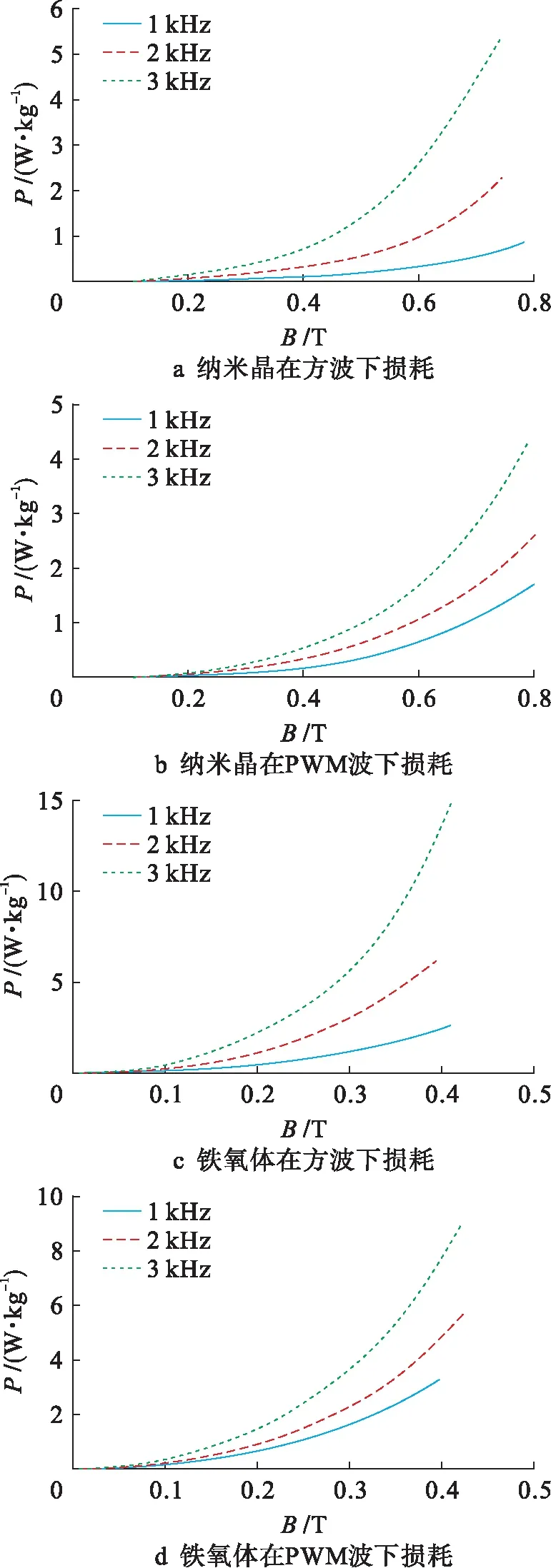
图2 非正弦激励下铁心损耗测量结果Fig.2 Measurement results of core loss under non-sinusoidal excitation
(6)
式中:r为涡流路径距中心的距离;E(r,t)为感应电动势;R为软磁铁氧体中涡流环路的电阻.E(r,t)和R可分别表示为
(7)
(8)
其中,a=h/d.于是,铁心中总涡流损耗表示为
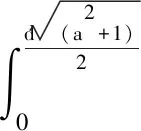
(9)
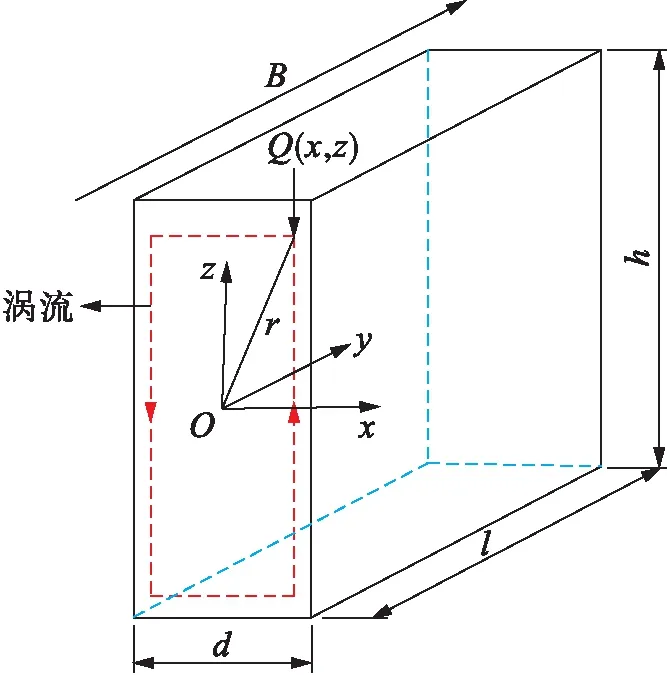
图3 矩形横截面铁心Fig.3 Core with rectangular cross-section
进一步地将磁通密度的时间微分用电压替换,得到矩形截面软磁铁氧体涡流损耗的计算公式为
(10)
式中:N为绕组匝数;U(t)为激励电压.
表1给出了利用式(10)得到的铁氧体铁心在非正弦激励下的涡流损耗计算公式,其中,D为占空比,f为频率.

表1 铁氧体铁心涡流损耗计算公式Tab.1 Calculation formulas for eddy current loss of ferrite core
2.2 基于Barbisio算法的异常损耗计算及改进
学者Barbisio提出一个任意激励形式下求取式(5)异常损耗系数的简化方法,认为异常损耗与频率1/2次幂成正比[14],两者的比例系数即为异常损耗的系数.为了分析上述Barbisio算法的模拟精度,本文基于爱泼斯坦方圈实验,测量了不同频率正弦激励下硅钢片的铁心损耗,如图4a所示.总损耗减去涡流损耗后,得到的异常损耗数据如图4b所示.根据Barbisio算法,该异常损耗与频率1/2次幂可近似为线性关系,但图4b表明在频率低于400 Hz时两者可近似为线性关系,而该直线的斜率为异常损耗系数;但高于这个频率,两者关系偏离线性,异常损耗系数也将无法用斜率表示.
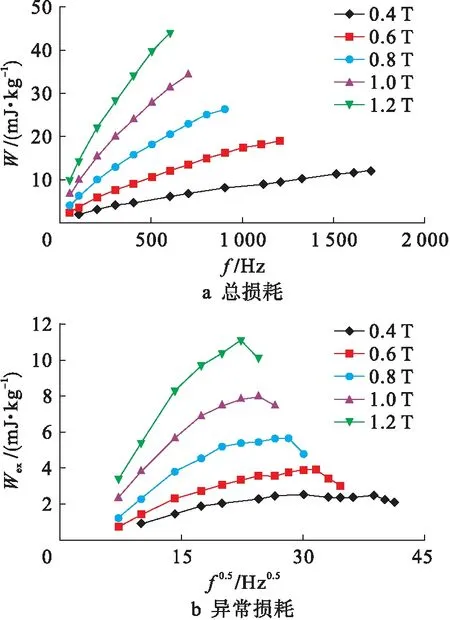
图4 正弦激励下硅钢片总损耗和异常损耗Fig.4 Total and excess loss of silicon steel sheet under sinusoidal excitation
为此,基于大量实测数据,本文建立了描述异常损耗系数与激励频率、励磁强度关系的数据库,并将三者关系拟合为
(11)
式中,C为损耗系数.图5给出了纳米晶铁心分别在方波和PWM波激励下,k(f,B)随B和f的变化情况.相应地,异常损耗计算为
(12)
2.3 模型验证
为了验证对Bertotti模型改进的可靠性,本文将模型计算结果Pmodeled与实验测量Pmeasured结果进行了对比分析,两者之间的误差定义为
(13)
图6给出了软磁铁氧体和纳米晶在方波、PWM波激励下损耗模型计算值与实验值的比较情况.可以看出,计算值与测量值吻合程度很好,验证了所提模型的计算精度.
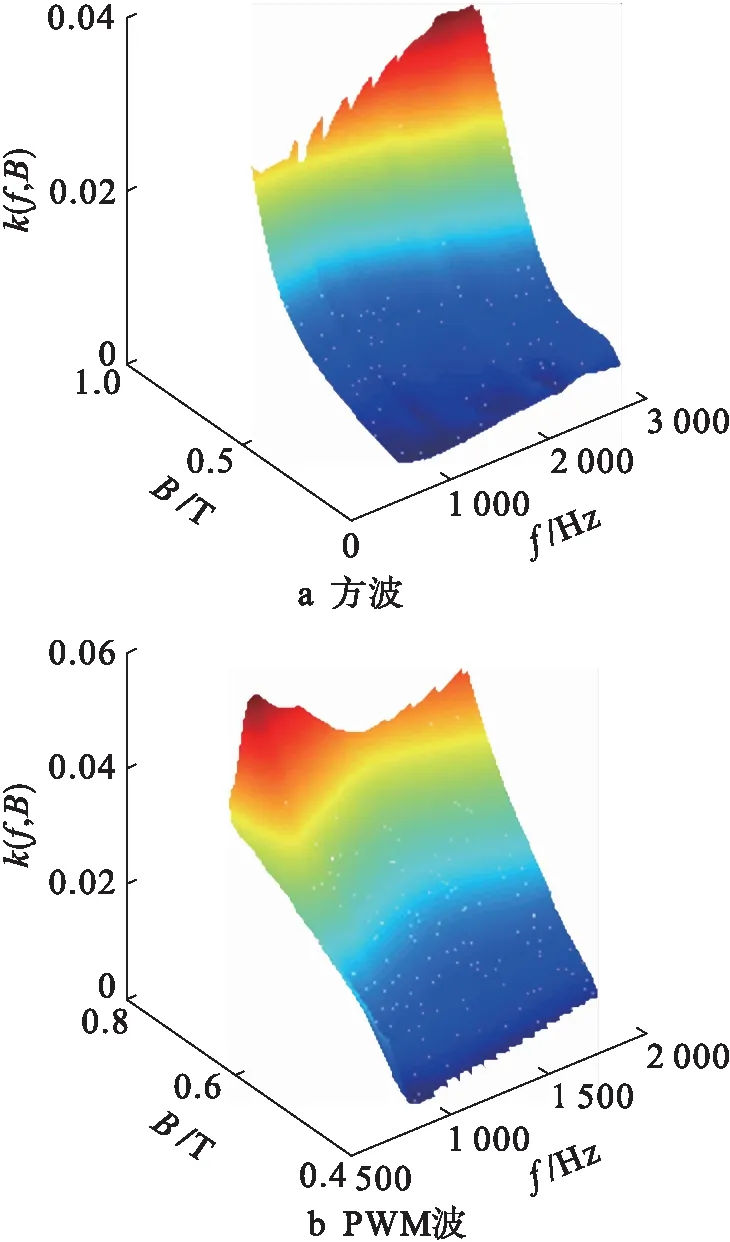
图5 异常损耗系数Fig.5 Excess loss coefficient
3 中频变压器铁心损耗
本文设计制作了一台中频电力电子变压器,仿真计算了6 kHz方波激励下空载损耗,并与实验测试值进行了对比.其中,变压器铁心材料为纳米晶卷绕铁心.
图7给出了该变压器仿真计算模型空载下铁心磁密分布,磁通密度最大值为0.581 T.根据铁心中各剖分单元磁通密度数值计算结果,结合式(11)计算得到异常损耗系数k(f,B),再利用式(12)计算异常损耗,最后得到铁心空载损耗计算值为13.52 W.
图8a为制作加工后的纳米晶铁心中频变压器实物图,图8b为实验现场测试结果.空载损耗实测值为13.9 W.计算值与实测值较好地吻合,验证了本文改进损耗模型的有效性.
4 结 论
本文搭建了软磁铁氧体和纳米晶环形铁心磁特性测量系统,建立了这两种铁心材料磁特性、损耗特性数据库;修正了Barbisio算法计算异常损耗的误差,提出表达异常损耗系数与励磁频率和强度的数学关系式,推导了矩形截面铁氧体铁心的涡流损耗计算方法,验证了改进的Bertotti损耗模型的计算精度.得到结论如下:
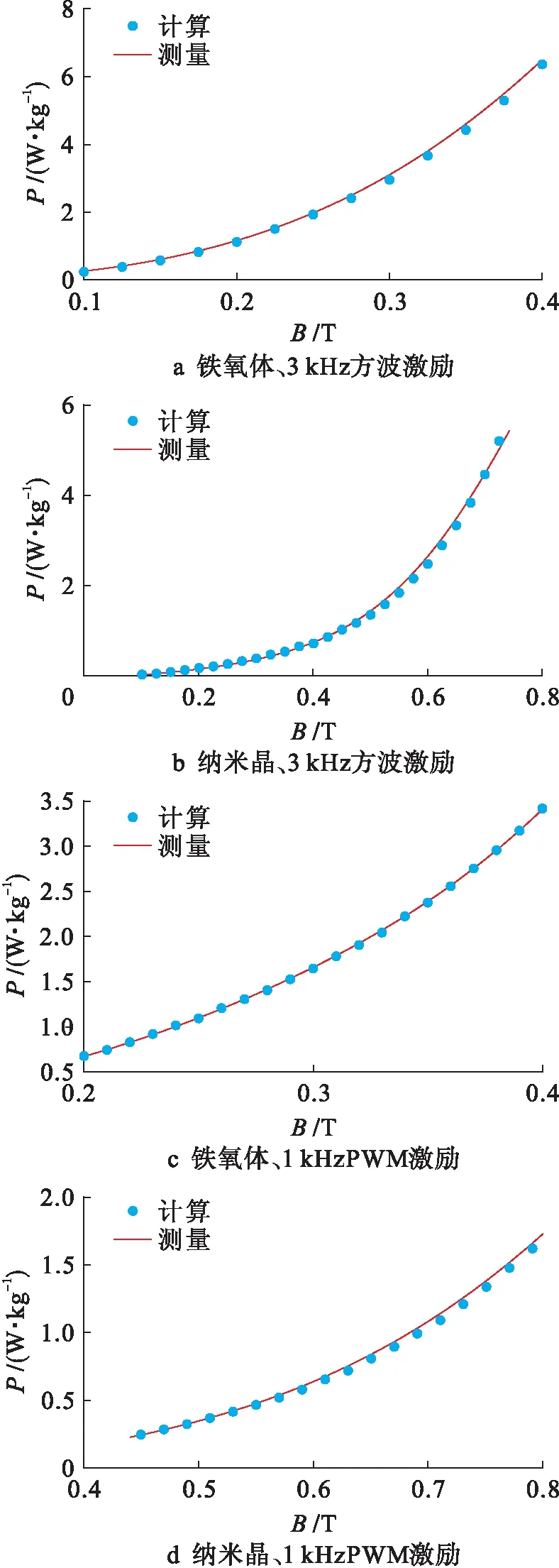
图6 损耗模型计算值与测量值的比较Fig.6 Comparison of calculated values by loss model with measured values
1) 软磁铁氧体和纳米晶环样铁心损耗特性测量结果表明:在同样励磁频率下,PWM激励下铁心损耗大于方波损耗;纳米晶的铁心损耗小于软磁铁氧体铁心损耗.
2) 将异常损耗系数表达为频率和磁密的函数后,提高了Bertotti损耗分离模型在方波及PWM等非正弦励磁下的铁心损耗计算精度.
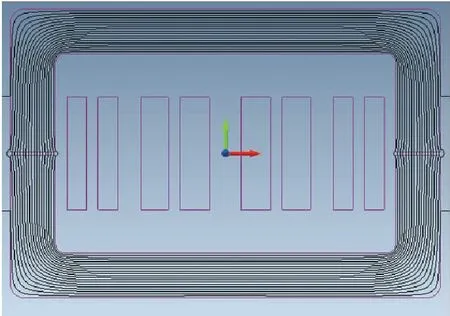
图7 6 kHz方波激励下中频变压器空载磁场仿真
Fig.7 Simulation for no-load magnetic field in medium frequency transformer under square wave excitation at 6 kHz
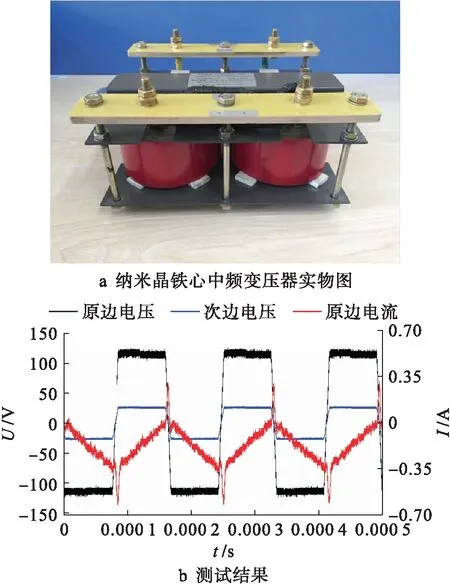
图8 中频变压器实物与实验测试Fig.8 Medium frequency transformer device and its experimental test
3) 中频变压器制作与空载实验测试结果验证了所提损耗计算模型的有效性.

