基于BP网络算法的大地测量误差检测技术*

王怀宝

(吉林建筑大学 测绘与勘查工程学院， 长春 130118)

大地测量的应用范围较广泛，可用于为工程地形测量提供基础的平面与高程控制，用于空间科学与国防建设的方位角、地理坐标精准定位与地球重力场数值测量，以及为地球相关活动研究提供数据信息[1-2].测量结果的误差影响因素包括测量设备与系统本身的误差，以及实际测量过程中测量精度引起的测量误差.各应用领域对大地测量结果的精准度要求均较高，对测量误差进行检测与补偿，能够进一步提升大地测量结果的准确性，进而提升工程领域建筑结构的稳定性，增加空间科学与地球活动研究领域结果的可信度[3-4].因此，大地测量误差检测是现阶段大地测量研究领域的重点课题，受到了很多专家与学者的重视，并研究出一些较好的误差检测方法[5].

文献[6]提出一种基于纳米精度的误差测量检测方法.该方法根据激光检测仪的基本原理，对工作台的测量误差进行累积分析，获取工作台测量镜面的初始数据，根据两组数据之间跨度间关系寻找出误差，并对其进行检测.该方法在误差检测中具有较高的检测效率，但是检测结果的准确度较低.文献[7]提出一种基于有限元模态分析的误差检测方法.构建传感器三维实体模型以及有限元模型，利用传感器蠕变进行有限元模态分析，得到不同装置的频率以及振型，根据谐响应分析确定最大模态频率，实现传感器测量误差检测.该方法检测精度较高，但是误差检测过程所需时间较长.文献[8]提出一种基于影响因素分析的关节臂式坐标测量误差检测方法.通过对测量力等因素引发的距离测量误差数据的理论分析，获得影响设备测量结果准确度的主要因素，构建测量设备测量头与待检测对象的部分形变、测量杆的弯曲形变的数学模型，利用该模型对实际测量值进行误差检测.该方法的检测效率较高，检测过程耗时较短，但检测结果的准确度较低.

针对上述方法存在的不足，提出了基于BP网络算法的大地测量误差检测方法，并通过实验验证所提方法的检测效率与准确率.

1 测量基本过程及测量点参数计算

1.1 大地测量基本过程

大地测量能够描述物体空间信息，是一种确定测量点精确坐标位置的测量方法，其装置结构如图1所示.整个测量装置包含三个非接触式激光测距传感器、两个传感器基座以及两个测量基准板.将传感器安装到对应的基座上，在横向上安装两个传感器，在纵向上安装一个传感器，将横向记作x方向，将纵向记作y方向；将测量基准板分别放置在x方向与y方向的两侧，在检测点设置标志物，并平稳移动各激光传感器位置，通过将传感器获取的数据进行组合计算，得到测量点在x方向和y方向的相对位移及其中心点绕垂直轴旋转角度.

根据测量装置的坐标系图，将x方向上的两个非接触式激光传感器在横轴上的投影点记作a1(x1，0)、a2(x2，0)，将y方向上的非接触式激光传感器在纵轴上的投影点记作b(y1，0).

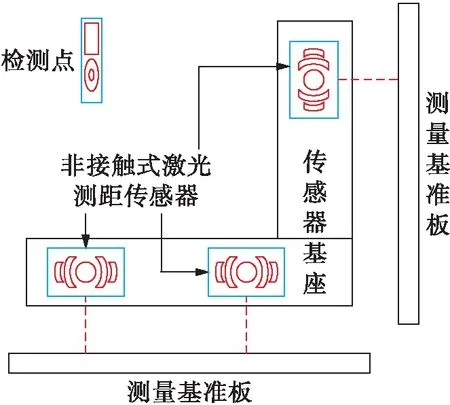
图1 大地测量装置结构图Fig.1 Structure of geodetic survey device

1.2 测量点相对位移及旋转角度计算

图2为测量装置进行测量的三维图示.图2中，点u、v、w分别表示某一时刻各传感器的位置坐标点，u、v的移动范围线段为O2O3，w的移动范围线段为O2O4，O1表示标志物的中心点对应的地面投影点，即测量点，I1、I2和I3为各传感器测量结果，得到u的坐标为(x1，I1)，v的坐标为(x2，I2)，w的坐标为(y1，I3)，综合三个点的坐标及线段O2O3与O2O4之间的垂直关系，得到O2O3与O2O4所在直线的方程式，即

(1)

(2)

图2 测量装置的三维图示Fig.2 3D illustration of survey device

对上述方程进行求解计算，得到O2的坐标为

(3)

(4)

根据O2点坐标、O1O2线段的长度以及线段O2O3与O2O4之间的夹角，得到测量点O1的坐标为

(5)

(6)

测量点O1绕垂直轴的旋转角度的计算式为

(7)

通过上述过程求出测量点在x方向和y方向的相对位移及绕垂直轴旋转角度，完成该测量点的大地测量.通过测量计算得到所需测量目标的测量值，其中，相对位移为准确值，而测量点绕垂直轴的旋转角度的测量结果存在误差.因此，通过BP网络模型对大地测量的旋转角度进行测量误差预测.

2 基于BP网络算法的检测技术设计

2.1 BP神经网络模型构建

BP神经网络是一种多层反向传播神经网络，其主要特点是在传播过程中信号向前传递误差反向输出.构建BP神经网络模型，利用动态贝叶斯检验算法对BP神经网络模型标准化处理得到的大地测量值的误差预估值进行概率计算[9-10]，进而判断某一时刻检测值是否存在误差，具体过程如下。

BP神经网络模型由输入层、输出层及隐藏层组成.输入层和输出层对应样本数据的输入集和输出集.BP神经网络可以看作一个非线性映射，即

F∶Rn→Rm，f(X1)=Y1

(8)

式中：f(X1)为映射函数；X1为输入样本集合；Y1为输出样本集合.对于样本集合，输入Xi∈Rn和输出Yj∈Rm则需要满足：

f(Xi)=Yj(i=1，2，…，k)

(9)

式中：Yj为第j个输出神经元；k为节点个数.输入层包含i个神经元，输出层包含j个神经元，隐藏层包含h个神经元.输入层的神经元需要接收外界输入给网络的数据，则输入层神经元的输出描述为

OUTk=g(INk)

(10)

式中：OUTk、INk分别为输出值与输入值；g(INk)为神经元映射计算.将不同层的神经元进行加权求和，获取激活值，利用激活函数进行变换计算，得到神经元输出值，则获取隐藏层的输出值为

(11)

式中：whk为隐藏层权值；ik为输出节点数；θi为旋转角度输出控制变量.输出层的输出值为

(12)

式中：wjk为输出层的增益调控权值；ij为数据观测值.

通过上述条件构建BP神经网络模型hj，即

(13)

2.2 大地测量误差检测概率计算

根据构建的BP神经网络模型计算大地检测误差概率，首先计算神经网络输出层误差及旋转角度输出权重，然后求出测量误差估计值，最后根据上述计算，采用动态贝叶斯检验算法，对估计值进行概率计算，完成基于BP网络算法的大地检测误差检验.

假设输出层中第i个神经元的期望输出值为αij，实际输出为Ypi，则输出层的误差Ep为

(14)

旋转角度所占权重wij及其误差E分别为

(15)

(16)

式中：Ydi为调整权值因子；f1为激发函数；N为样本容量.计算得到第k时刻测量误差的估计值Δr(k)为

(17)

式中：Hk为输出层节点数；Ik为输入层节点数；Hi为隐藏层节点数.其中，输入层节点数为输入向量维数，输出层节点数为测试分类个数，隐藏层计算公式为

(18)

隐藏层节点数必须小于训练样本数，否则网络模型的系统误差与训练样本的特性无关而趋于0，即建立的网络模型没有泛化能力，也没有任何使用价值，同理，输入层的节点数也必须小于样本训练数.

利用动态贝叶斯检验算法对BP神经网络模型标准化处理得到的大地测量值的误差预估值进行概率计算，进而判断某一时刻检测值是否存在误差，完成基于BP网络算法的大地测量误差检测，概率dig计算公式为

(19)

3 实验结果与分析

为了验证基于BP网络算法的大地测量误差检测方法的误差检测性能，本文进行了实验，实验环境为WindowsXP SP3操作系统，软件配置采用svmlib检测系统.在该系统中模拟大地检测过程，计算出测量点绕垂直轴的旋转角度，采用构建的BP网络模型计算测量数据的误差，并根据大地检测误差概率计算公式计算检测误差的准确率.

本实验数据取自于GIS系统，它是对全部或部分地球表层空间中的有关地理分布数据进行采集、储存、管理、运算、分析、显示和描述的技术系统.从系统数据库中随机选择2个大地检测数据集S和D分别作为实验数据集和对比数据集，每个数据集包含100个数据，分别计算2个数据集中测量点绕垂直轴的旋转角度，作为误差检测数据，如表1所示.由于构建神经网络的输出数量取决于输入值的设定，因此，设置输入层的输入节点为4，则隐藏层的输出节点为5，输出层的输出节点为3.神经网络构建图如图3所示.

表1 实验数据集及对比数据集数据Tab.1 Data in experimental and comparative datasets (°)

采用所提检测方法与基于纳米精度的测量误差检测方法以及基于有限元模态分析的误差检测方法进行实验，三种方法分别用A、B、C表示，分别对比三种误差检测方法的检测准确率、检测成本开销及检测时间.

3.1 检测准确率对比实验

图4为不同方法误差检测准确率对比.由图4可知，随着数据数量的增加，三种不同方法的检测准确率均呈现上升趋势.当数据个数为20个时为检测准确率最低值，所提测量误差检测方法的检测准确率平均值约为83%，基于纳米精度的测量误差检测方法的检测准确率平均值约为64%，基于有限元模态分析的误差检测方法的检测准确率为71%.对比三种不同方法的实验结果可知，所提测量误差检测方法的检测准确率高于实验对比的另外两种方法，且误差检测准确率最高可达90%以上.这是由于所提方法在分析大地测量基本原理的基础上，通过测量待测量目标的坐标点和角度等相关参量，采用BP网络的映射分析，测量误差预测模型；根据模型设定输入值和输出值得到预测误差，并利用动态贝叶斯检验算法对得到的预测误差进行概率计算，能够提高所提方法的检测准确率.

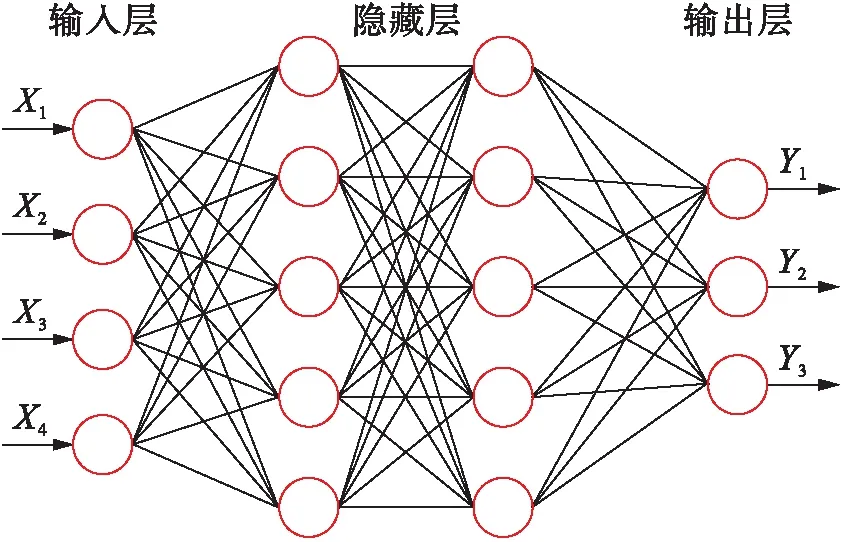
图3 神经网络构建图Fig.3 Construction of neural network

图4 不同方法误差检测准确率对比Fig.4 Comparison of detection accuracy with different methods

3.2 检测成本及检测时间对比实验

采用所提检测方法与基于纳米精度的测量误差检测方法以及基于有限元模态分析的误差检测方法进行检测成本开销对比，结果如表2所示.表2中，C为成本开销，表示使用检测设备耗用的电费等一系列成本费用的总数.成本开销的计算公式为

(19)

式中：W为消耗电费总额；g为产品产量.

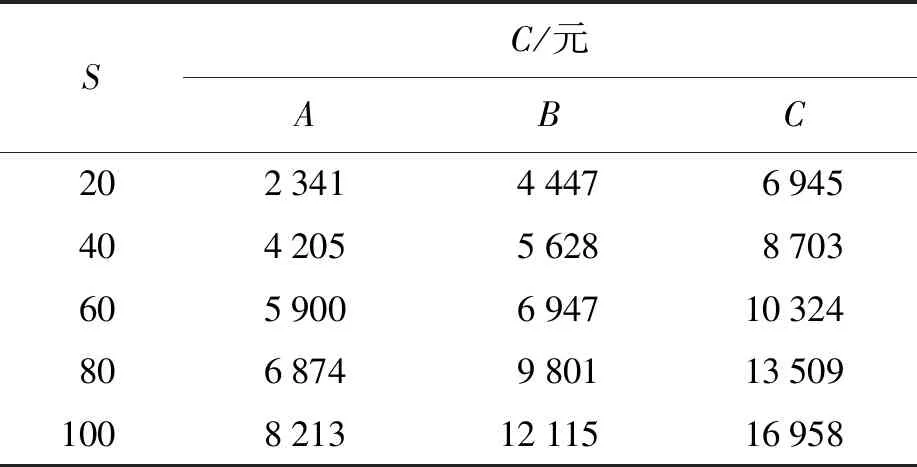
表2 不同方法检测成本开销对比Tab.2 Comparison of cost with different methods

分析表2可知，随着检测数据的不断增加，三种方法检测所需成本开销也随之增加，当数据个数为40个时，所提方法检测成本消耗为4 205元，基于纳米精度的测量误差检测方法的检测成本消耗为5 628元，基于有限元模态分析的误差检测方法的检测成本消耗为8 703元，对比可知，所提方法检测成本消耗分别比基于纳米精度的测量误差检测方法和基于有限元模态分析的误差检测方法的检测成本低823、3 498元.随着检测数据个数增加，所提方法成本消耗均小于对比方法，证明所提方法检测成本开销最低.

采用所提测量误差检测方法与基于纳米精度的测量误差检测方法以及基于有限元模态分析的误差检测方法进行检测时间的对比，结果如表3所示.

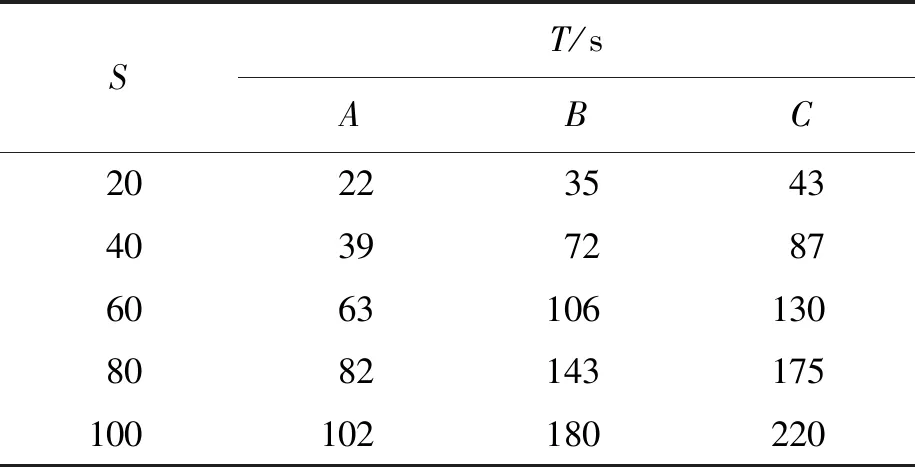
表3 不同方法检测时间对比Tab.3 Comparison of detection time with different methods

分析表3数据可知，三种方法的检测时间都随着检测数据数量的增加而增长，当检测数据个数为60个时，所提测量误差检测方法与基于纳米精度的测量误差检测方法以及基于有限元模态分析的误差检测方法的检测时间分别为63、106和130 s，所提方法的误差检测时间最少；当检测数据数量增加到100个时，所提测量误差检测方法与基于纳米精度的测量误差检测方法以及基于有限元模态分析的误差检测方法的检测时间增加量分别为39、74、90 s，所提方法的检测时间增加量最少.通过对检测成本及检测时间的对比实验，证明所提测量误差检测方法的检测效率最高，检测稳定性优于实验对比方法.

BP网络算法能够利用分层来同时处理全部数据，因此，对大地测量误差检测的时间较快；通过隐藏层的择优计算，最终能够得到最精确的误差率；BP神经网络算法计算时间快，且所需的器材较少，因此其检测成本较低.综上所述，采用BP神经网络算法检测大地测量过程中的误差，检测成本低、时间快、且能够准确检测出大地测量过程中产生的误差.

4 结 论

为了提高大地测量误差检测方法的准确率与效率，提出基于BP网络算法的大地测量误差检测方法.通过对BP神经网络中神经元的映射分析，构建误差预测的BP网络模型，利用所构建模型对测量结果进行测量误差预测.为了提高误差检测结果的准确性，利用动态贝叶斯检验算法对BP神经网络模型标准化处理，对误差预测结果进行概率计算，并根据计算结果判断测量结果是否存在误差.通过实验证明设计方法误差检测准确率及效率高，能够有效检测大地测量中的误差.

未来阶段，将对影响大地测量结果精准度的影响因素进行深入研究，从多方面进行测量结果的误差分析与补偿，进一步减小大地测量误差，提高大地测量数据的准确性.