基于GaN HEMT的双向DC-DC变换器系统损耗分析

高圣伟，祁树岭，孙醒涛，贺 琛，董晨名

（1.天津工业大学 电工电能新技术天津市重点实验室，天津 300387；2.天津金沃能源科技股份有限公司，天津300387）

全桥双向DC-DC 变换器（double active bridge，DAB）系统应用广泛，特别在直流电网、电力系统和电动汽车中都充当了重要的角色[1-3]。而开关器件作为系统最重要的组成部分之一，正确地选择合适的开关器件显得尤为重要。第三代半导体器件氮化镓（GaN）具有低损耗、高结温、宽带隙等优异的性能，具有较好的工程应用前景[4-8]。现阶段，GaN 普遍采用共栅共源（Cascode）结构，其使用一个Si 做衬底，级联一个GaN器件，即高电子迁移率型氮化镓（gallium nitride high electron mobility transistor，GaN HEMT）[9-11]。

已有很多文献对DAB 系统损耗进行了分析：文献[12]对系统损耗进行了分析，但没有分析详细的工作过程。文献[13]给出了系统的整体损耗分析，其开通、关断损耗通过查找数据手册所得，系统分析的准确度方面还存在一定欠缺。文献[14]对Cascode 结构进行了建模，但没有具体分析寄生参数对暂态损耗的影响。文献[15]给出了考虑寄生参数的GaN HEMT 器件模型，但在计算暂态损耗时未考虑寄生参数的影响，使所得损耗与实际损耗仍然存在一定误差。

GaN HEMT 器件内部存在各种寄生参数，而在以往DAB 系统中并未充分分析其影响。详细分析GaN HEMT器件寄生参数在不同工作阶段下的损耗模型，有助于建立更完善的DAB 损耗模型，实现DAB 系统损耗的精细计算，使损耗模型更贴近实际，以便正确评价全桥双向DC-DC 变换器的全系统能耗。基于此，本文对DAB 系统的动态工作过程进行分析，建立精细化的DAB 系统损耗模型，深入研究在单重移相（single phase shift，SPS）控制下不同时间段 GaN HEMT 在系统中的开通、关断损耗，给出了GaN HEMT 器件的通态损耗以及系统中变压器损耗的计算方法，并搭建基于Cascode 型GaN HEMT 的全桥双向DC-DC 变换器仿真和实验平台，验证本文建立的DAB 系统损耗模型的正确性。

1 器件的结构及其工作原理

1.1 器件结构

图1 为Cascode 型GaN HEMT 高压级联机构，Si MOSFET 的漏极连接到耗尽型GaN HEMT 的漏极，耗尽型GaN 的栅极与Si MOSFET 的源极相连，并且低压Si MOSFET 与耗尽型GaN HEMT 的电位相反，低压Si MOSFET 作为开关提供负偏压，控制耗尽型GaN HEMT的开通与关断[15]。

图1 高压Cascode 型GaN HEMT 结构Fig.1 Structure of GaN HEMT with high voltage Cascode type

为分析GaN HEMT 器件工作状态的损耗，在器件内部引入了寄生参数，其结构如图2 所示。

图2 中：第1 个重要参数是寄生电感包括栅极电感LG、源极电感LS、漏极电感LD，其中，内部引线寄生电感包括Lm1、Lm2和Lm3；第2 个重要参数是寄生电容包括 6 个结电容，即栅源极电容（CGS_Si、CGS_GaN）、栅漏极电容（CGD_Si、CGD_GaN）、漏源极电容（CDS_Si、CDS_GaN）；第 3 个重要参数为跨导GM，表示通道电流随开关器件栅极到源极电压之间增量的变化，它决定了电压和电流的过渡时间：

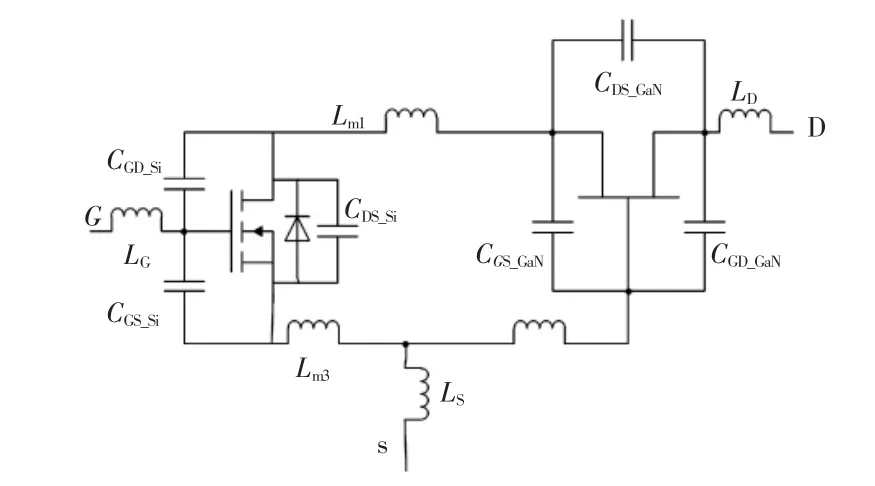
图2 Cascode 型GaN HEMT 等效模型Fig.2 Equivalent model of GaN HEMT with Cascode type

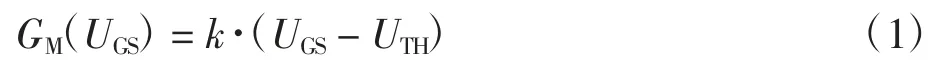
式中：参数k 的值来自于数据手册。需要说明的是，GaN HEMT 器件内部电阻均未在图2 中表示，在系统中Lm2的影响较小，故分析中未给出。

1.2 单重移相工作原理

图3 为全桥双向DC-DC 变换器拓扑。图3 中：Q1—Q8为功率开关器件；等效漏电感LR与高频隔离变压器在中间连接两个全桥；UAB、UCD分别代表变压器高压侧的电压和变压器低压侧的电压。SPS 控制是高压全桥H1超前或滞后低压全桥H2一个α 角度，从而实现全桥之间的能量传输。正向传输如图4 所示。

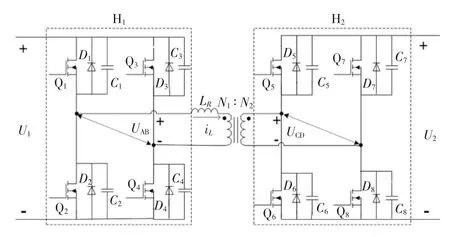
图3 全桥双向DC-DC 变换器拓扑Fig.3 Topology of double active bridge

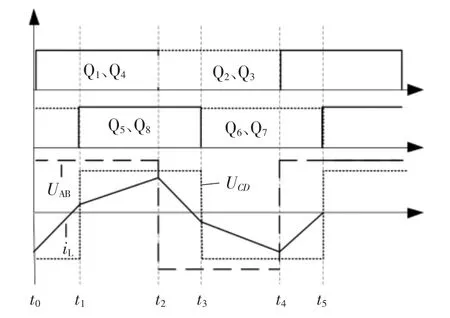
图4 单移相控制正向工作模式Fig.4 Forward mode of single phase shift control

图4 中，同一全桥下的同一桥臂互补导通，各导通 180°。iL为电感电流，D 为移相比，0≤D≤1，如式（2）所示：

2 系统损耗计算

2.1 常规DAB系统中的暂态损耗计算

常规DAB 系统中的暂态损耗计算各有不同，文献[12]中暂态损耗计算公式为式（3）：

式中：VDS为开关器件漏源极电压；iL为电感电流。文献[13]中暂态损耗计算公式为式（4）：

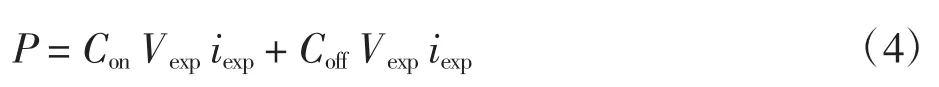
式中：Con和Coff均为提取损耗参数；电压Vexp和电流iexp分别为开通、关断时刻所测值。文献[15]给出的暂态损耗计算公式为式（5）：

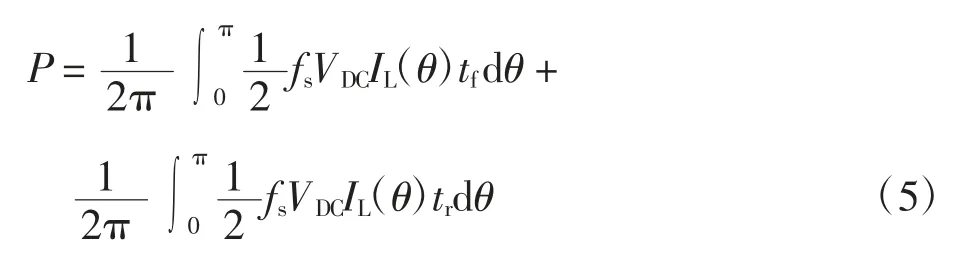
式中：tf为开通管的上升时间；tr为开通管的下降时间；fs为工作频率；VDC为开关器件漏源极电压；IL为电感电流。式（3）、（4）、（5）都能计算暂态损耗，但都没有分析寄生参数的影响，因此，所得暂态损耗值不够精确。

2.2 DAB系统中暂态损耗计算分析

2.2.1 GaN 正向导通过程

在 SPS 中，GaN HEMT 开关器件 Q1、Q4同步开通关断，在t0时刻Q1、Q4由关断状态转变为开通状态，Q5、Q8为关断状态，Q6、Q7为开通状态。因此，以 Q1为例，分析正向导通过程，开通可分为6 个状态。

第 1 阶段：t0时刻，UG输出一个高电压，开始给低压Si MOSFET 栅源极电容CGS1_Si充电，与Q1互补导通的Q2为关断后的反向导通续流状态。此阶段损耗忽略不计。

第2 阶段：当UGS1_Si数值上升到与阈值电压UTH_Si相等时，Q1中的 Si MOSFET 开始导通，UGD1_Si和 UDS1_Si电压下降，同时UGS1_GaN也开始放电，电压下降。此阶段耗尽型GaN HEMT 未开通。因此，没有电流流过GaN HEMT 晶体管。考虑此过程的寄生参数影响的电路如图5 所示。

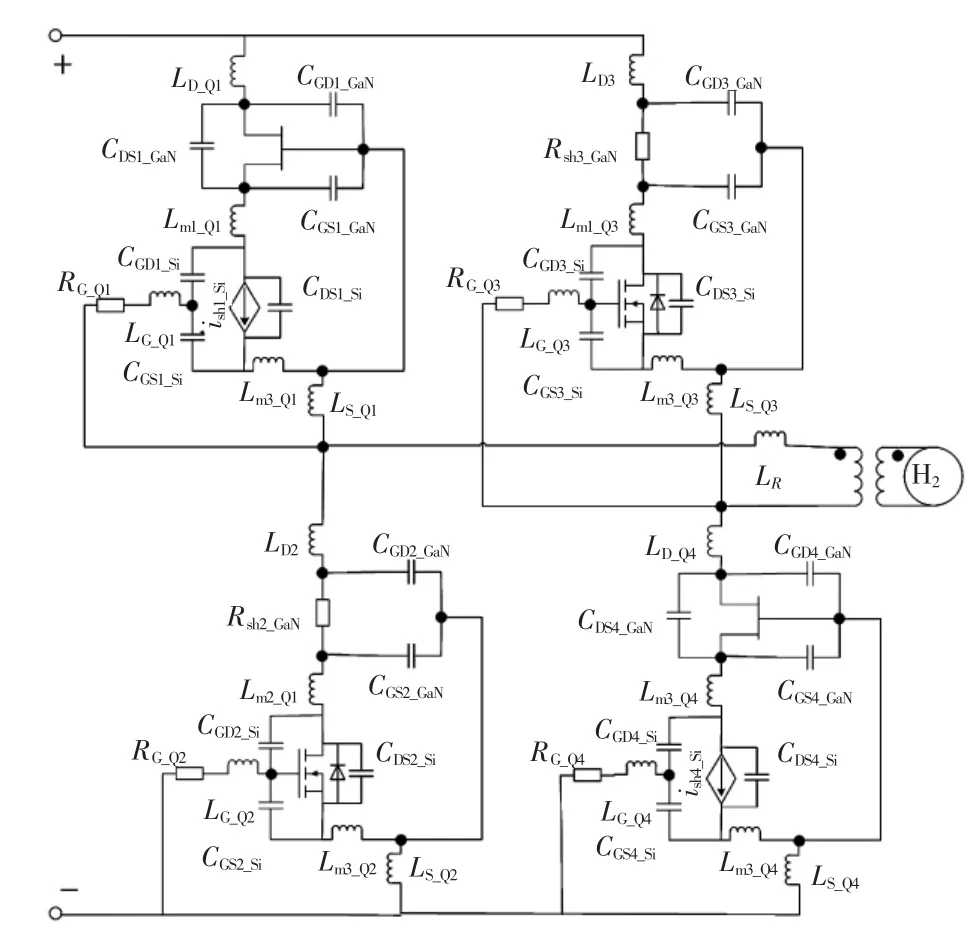
图5 正向开通第2 阶段Fig.5 Forward opening stage Ⅱ

图5 中的电路关系如式（6）所示：

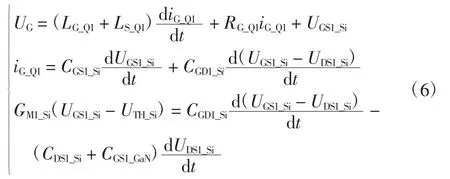
在此阶段，Si MOSFET 沟道消耗存储在CGD1_Si、CDS1_Si和CGS1_GaN中的能量。功率损耗计算为：

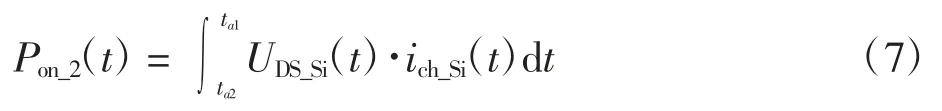
第 3 阶段：当 UGS1_GaN= UTH_GaN时，Q1的 GaN HEMT 开始工作导通，同时UGD1_GaN和UDS1_GaN电压下降。此时，Q2依然处于反向续流状态，其漏源极两端电压为零。流经电感的电流增加，Q1、Q2开始换流。考虑此过程的寄生参数影响的电路如图6 所示。图6 中电路关系如式（8）所示：

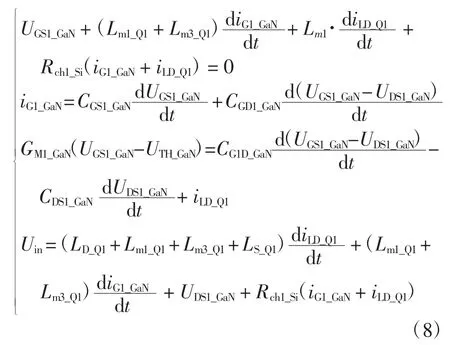
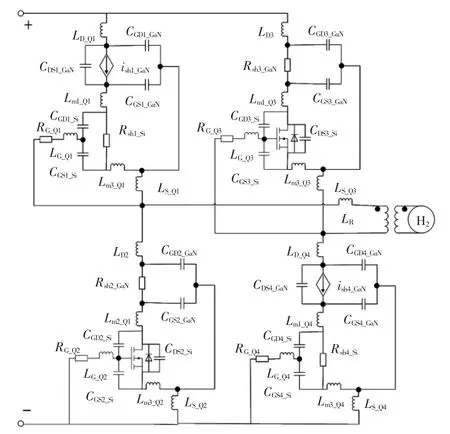
图6 正向开通第3 阶段Fig.6 Forward opening stage Ⅲ

图6 中，RG相当小，由于UGS1_Si继续增大，因此，UDS1_Si很快降低到0，并且可以认为Si MOSFET 在饱和区域中工作。UGS1_GaN的值随着GaN HEMT 的米勒效应变动而变化，此时Lm1为共用电感，影响着2 个内部Si MOSFET 和GaN HEMT，并且此时他们是独立工作的。在此阶段，电流iLD很快上升到iL，损耗主要来自于GaN，可以计算为：

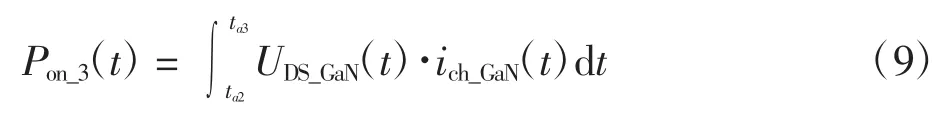
第4 阶段：当换流结束后，Q2开始反向恢复过程，模型与关键方程和第3 阶段相同。

第5 阶段：当Q2开关管中的Si MOSFET 结束反向恢复过程后，Q1中电容CDS1_Si开始放电，Q2漏源极电压从0 逐渐增加，等到和阈值电压UTH_GaN相等时，Q2中的 GaN HEMT 关断。第 4、5 阶段损耗 Pon_4(t)、Pon_5(t)和第3 阶段损耗计算公式相同，只是时间间隔不同。

第6 阶段：当Q1的漏源极电压UDS=UTH_GaN时，Q2漏源极电压继续上升，直到Q1中UDS1_Q1=0 为止。此阶段损耗忽略不计。

2.2.2 GaN 正向关断过程

在t2时刻，开关管Q1、Q4由持续开通变为开始关断，Q5、Q8为开通状态，Q6、Q7为关闭状态。以 Q1为例分析正向关断过程。

第1 阶段：Q1的驱动信号由高电平变为低电平，Q1中的Si MOSFET 的栅源极电压UGS1_Si开始下降。此阶段损耗忽略不计。

第 2 阶段：随着 Q1中的 UGS1_Si开始下降，Si MOSFET 进入饱和状态，Si 沟道饱和电流小于iL，剩余电流流向CDS1_Si，因此UDS1_Si电压上升。由于并联关系，UGS1_GaN电压上升。此过程结束时，UDS1_Si＜UTH_Si。 该过程具体分析电路如图7 所示。

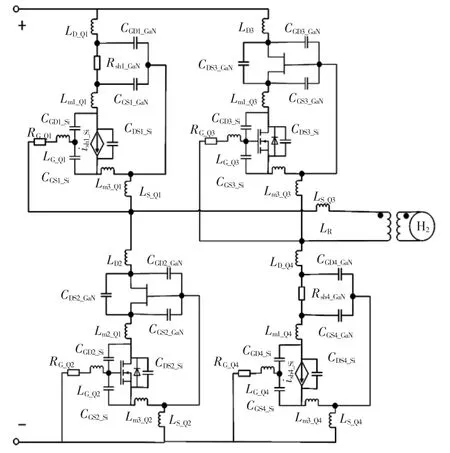
图7 正向关断第2 阶段Fig.7 Forward turn off stage Ⅱ

图7 中电路关系如式（10）所示。

此阶段GaN HEMT 的开关损耗可忽略不计，所以该阶段损耗由Si MOSFET 产生：

第3 阶段：随着UGS1_GaN的变化，流经GaN HEMT的沟道饱和电流ich_GaN小于电感电流iL，因此，过量电流流向CDS1_GaN，导致GaN HEMT 的漏源极电压升高。在此时刻，认为DAB 系统中开关器件Q1中的Si MOSFET 回路和GaN HEMT 回路是解耦的，而Q1中的漏源极电容继续放电直到CDS1_Si=0。受电感电流iL流动的影响，Si MOSFET 的电容两端电压 UDS1_Si和UGD1_Si持续上升，GaN HEMT 的电容两端电压UGS1_GaN继续下降。电路关系如式（12）所示：

GaN HEMT 沟道电流从iL非常快地减小到零。UDS1_GaN在短暂转变期间略微上升。关断损耗非常小：

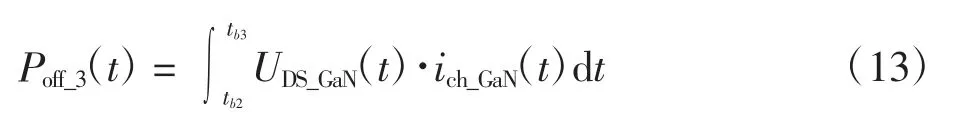
第 4 阶段：当 Q1中 UGS1_GaN＜UTH_GaN时，Q1开关管完全关断，此时开关管中电流给电容CDS1_Si、CDS1_GaN、CGD1_GaN充电。Q1中漏源极电压与Q2中交换。此阶段损耗过小忽略不计。

第 5 阶段：当 Q2中的 UDS2_GaN= UTH_GaN时，Q2中GaN HEMT 由关断变为开通状态。同时，Q2中漏源极电压继续下降，直到UDS2=0。之后结电容与电感LR谐振，实现开关管间能量互换。此阶段损耗忽略不计。

通过推导，可得DAB 系统的开通、关断总损耗为：

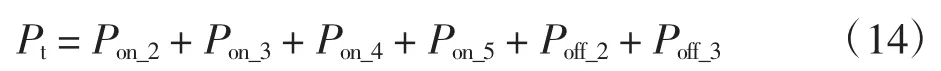
GaN HEMT 寄生参数由有限元仿真软件Ansoft Q3D Extractor[16]和器件数据手册[17]得到，如表1 所示。

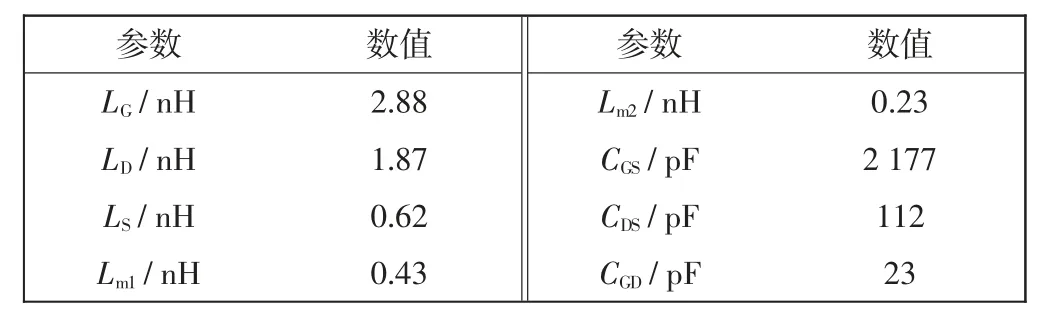
表1 GaN HEMT 寄生参数Tab.1 Parasitic parameters of GaN HEMT

2.3 通态损耗

系统稳定时，流经开关器件和体二极管的通态电流与器件之间的通态压降会产生通态损耗。在不考虑温度的情况下，通态损耗是对器件当时电压与电流的乘积进行积分，而且开关器件与体二极管的参数不同，故要分开计算。

式中：VF1为开关器件的通态压降；VF2为并联二级管的通态压降；Id为器件的漏极电流。在DAB 系统一个完整的工作周期内，流过开关器件的电流次数为Y，流经体二极管的次数为Z。在高压侧全桥Y=Z=2，而低压侧全桥 Y=2，Z=3。

综上所述，系统开关器件的总体损耗为：

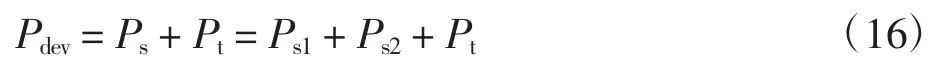
2.4 变压器损耗

变压器中的损耗包括铜损耗和铁损耗，电感LR以外加形式出现。变压器可以等效为T 型电路，如图8所示。图8 中：RS1、LS1、RS2′、LS2′、RM、LM为变压器等效参数；RN、LN为独立电感的等效电阻和电感。

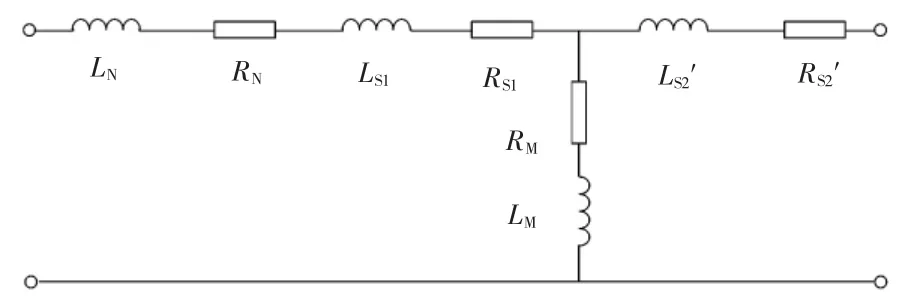
图8 变压器等效电路Fig.8 Equivalent circuit of transformer

利用变压器综合测试仪TH2829LX，在频率为20 kHz、测试电压为1 V 条件下测得变压器一、二次侧的励磁阻抗和漏磁阻抗，如表2 所示。

表2 变压器等效参数Tab.2 Equivalent parameters of transformer

由于流过RM、LM的电流较小，所以忽略励磁支路的损耗。铜耗的计算公式为：

式中：INS为流经变压器的电流有效值。除此之外，变压器的另一项损耗为铁芯损耗。针对铁芯损耗问题，本文激励为矩形波，即非正弦波激励。此时损耗会比正弦激励条件下更大，采用改进的MSE（Modified SE）方法[18]计算，即

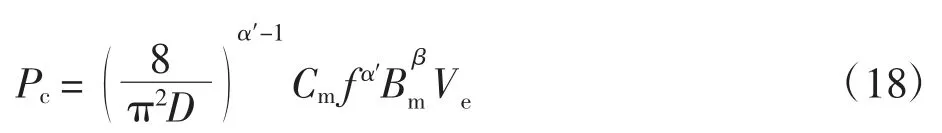
式中：Cm为磁芯损耗密度；α′和 β 为常数系数；Bm为峰值磁感应强度；Ve为铁芯体积；D 为占空比。所用变压器铁芯为2 个E65 型磁铁组合而成，查阅文献[19-20]可得变压器铁芯参数，如表3 所示。

表3 变压器铁芯参数Tab.3 Parameters of transformer core

磁感应强度计算为：

式中：Im为流经电感电流的峰值；N1为一次侧线圈匝数；Le为E 型磁铁的有效长度；μ0为真空磁导率，根据数据手册[14]可得磁导率μr。求解峰值磁通密度Bm的公式为：

通过式（18）可得Pc损耗。变压器整体损耗为：

DAB 系统的整体损耗为：

3 仿真与实验

采用Transphorm 公司生产的TPH3205WSB GaN HEMT，将它应用在全桥双向DC-DC 变换器系统中，用LT Spice 仿真软件对系统进行精细仿真，仿真条件为 fs=20 kHz，U1=250 V，变压器变比为 5 ∶1。在此基础上搭建0.5 kW 的DAB 实验样机，以验证结论的正确性。按照仿真条件搭建实验平台，如图9 所示。

图9 硬件实验平台Fig.9 DAB hardware platform

仿真图形如图10 所示，为正向传输模式，移相角α 为30°，选取输入功率为0.2 kW。

图10 中：UAB为变压器高压侧电压；UCD为变压器高压侧电压；电流iL、iL2分别为变压器高压侧、低压侧电感电流。实验结果如图11、图12 所示。其中，图11、图12 中电流探头测得电感电流换算规则为0.5 A/V。

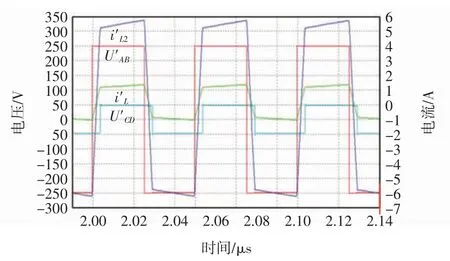
图10 仿真图形Fig.10 Simulation images

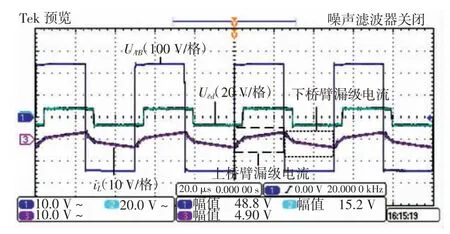
图11 变压器两端电压，一次侧电流波形Fig.11 Voltage across transformer，primary side current

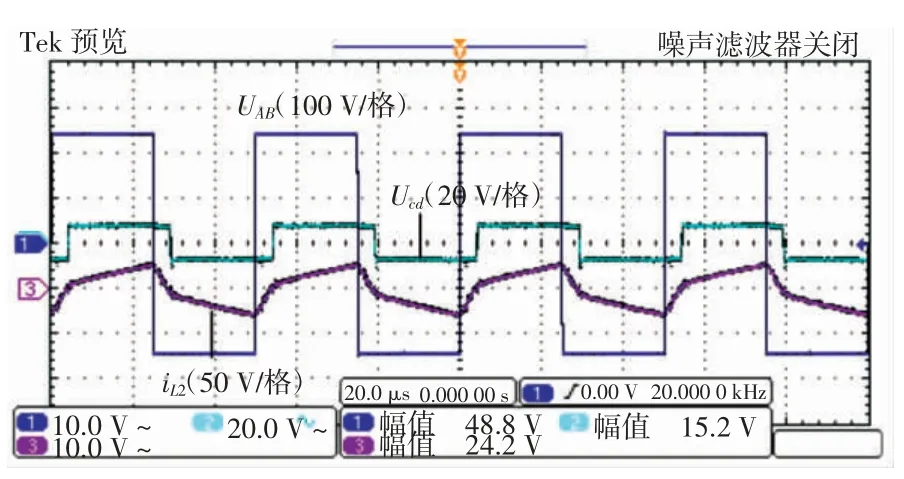
图12 变压器两端电压，二次侧电流波形Fig.12 Voltage across transformer，secondary side current

实验通态损耗值通过图11 中电压电流积分的方法算得，其中电流指的是一周期内电感电流iL分成上下桥臂开关器件的漏极电流。然后模拟实验条件测得变压器损耗，最后通过差值计算得到暂态损耗，并与计算得出的理论损耗值进行对比。在输入功率为0.2 kW时，各部分损耗如图13 所示。在20 kHz SPS 控制模式下，效率曲线对比结果如图14 所示。

由图13、图14 可知，由于小功率传输即0.4 kW以下存在回流功率，此时DAB 系统实验平台所得传输效率平均约为92.3%，与文献[21]中系统实验数据基本吻合。由于在理论计算中忽略了导线的寄生参数损耗以及实验条件的限制，理论模型效率比实际DAB 系统效率要高约1%。图14 中参考模型1、2、3 分别为式（3）、式（4）、式（5）计算所得，这 3 种模型损耗计算中未加入寄生参数，所以算得损耗较小，传输效率更高。通过对比分析上述4 种模型，本文所建立的损耗模型对器件开通、关断损耗的分类更加全面，结果更加接近于实验真实值，使得本文损耗数值准确度提升了近0.88%～1.14%，与系统真实损耗仅差约0.71%。

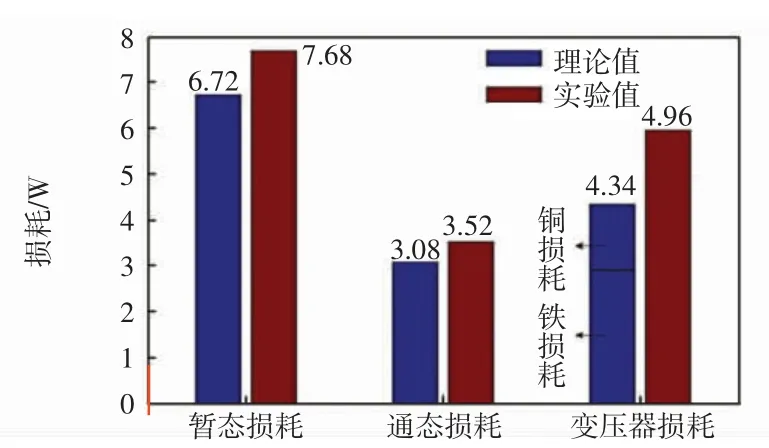
图13 系统损耗Fig.13 System loss

图14 DAB 效率曲线Fig.14 DAB efficiency curve

4 结 语

在针对已有DAB 系统的暂态损耗计算中发现，其建立的损耗模型计算得出的数值与实际实验值相差较大。鉴于此，本文将型号TPH3205WSB GaN HEMT应用在DAB 系统中，在SPS 控制下，建立了一种精细化DAB 系统损耗模型：

（1）提出了一种DAB 系统的精细开通、关断损耗模型，考虑GaN HEMT 的寄生参数影响下，详细分析了每个阶段的动态过程，并在此基础上算得了系统的开通损耗和关断损耗。

（2）给出了GaN HEMT 通态损耗、高频变压器及电感的稳态损耗计算方法，提高了系统损耗计算的准确性。

（3）搭建了实验平台进行验证，与文中其它3 种参考模型的损耗进行分析对比，本文损耗模型所得数值准确度提升了近0.88%～1.14%，与实验真实损耗数值仅差约0.71%。