数学教学中的辗转相除法

福建省福州第七中学 黄志鹏

一、历史来源

辗转相除法是目前仍然在使用的历史最悠久的算法之一。它首次出现于几何原本（卷7 命题1-2、卷10 命题2-3）（大约公元前300 年），而在中国则可以追溯至东汉出现的《九章算术》 。在卷7中用于整数，在卷10 中用于线段的长度（也就是现在所说的实数，但是当时未有实数的概念）。卷10 中出现的算法是几何的，两条线段a 和b 的最大公约数是准确测量a 和b 的最大长度。

二、简介

在数学中，辗转相除法又称欧几里得算法，是求最大公约数的算法。同时出现在高中教材人教A 版必修三第一章第四节。在教学中，辗转相除法是算法教学的经典案例，我们有必要加深教师对该案例的理解，加强对于学生对数学的深入学习，提高对数学学科的学习热情。因此，我们很有必要对辗转相除法的原理及应用进行探索。

三、最大公约数的应用

1.最大公约数的定义

整数a1，a2，a3，…，an的公因数中最大的一个叫作最大公约数，记作（a1，a2，a3，…，an），若（a1，a2，a3，…，an）=1，我们则说a1，a2，a3，…，an互质或互素。

2.最大公约数的求解方法

例1：求20、30 和36 的最大公约数。解法一： 列举法。

20 的因数有：1、2、4、5、10、20。

30 的因数有：1、2、3、5、6、10、15、30。

36 的因数有：1、2、3、4、6、9、12、18、36。

三个数的最大公约数是2。解法二：分解质因数的方法。

20=2×2×5，

30=2×5×3，

36=2×2×3×3，

（20，30，36）=2。解法三：短除的方法

（20，30，36）=2。

小结：在计算三个数的最大公约数的时候，要找三个数的公有的质因数，如果其中的两个商还有质因数，也不要往下除。

例2：求18 和24 的最大公约数。

解：（1）用分解质因数的方法独立完成。

（18，24）=2×3=6。

[18，24]=2×3×3×2×2=72。

（2）观察发现：18×24=4×72。

小结：两个自然数的最大公约数的一个重要性质是：两个自然数的乘积等于这两个自然数的最大公约数和最小公倍数的乘积。

延伸：若a、b 表示两个自然数，则 a×b=（a，b）×[a，b]。

例3：两个数的最大公约数是6，最小公倍数是504，如果其中的一个数是42，那么另一个数是多少？

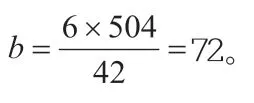
3.利用最大公因数解决实际问题

例4：有320 个苹果，240 个橘子，200 个梨。用这些果品，最多可以分成多少份同样的物？在每份礼物中，苹果、橘子和梨各有多少个？

分析：根据题目的要求，在分礼物的时候必须正好分尽3 样果品。因此，礼物的份数必须是320、240 和200 的公因数，现在还要求最多可以分成多少份同样的礼物，也就是说要求320、240 和200 的最大公因数。

解：用短除法：

（320，240，200）=2×2×2×5=40。

因此，最多可以分成40 份，每份礼物中有苹果320÷40=8（个），橘子240÷40=6（个），梨200÷40=5（个）。

四、辗转相除法在解题中的应用

1.两个有理数公因数的求法

2.两个无理数公因数的求法

其中，a 为任意实数，甚至可以是多项式。

4.运用辗转相除法把最大公约数表示为某量整数的倍数和

定理：若（a，b）=d，则必有二整数k、l 使得d=ka+lb。

例7：求一组整数x、y，使得150x+42y=（150，42）。

解：我们可以将辗转相除过程写成横式(主要是在于应用欧拉演段)：

得到6 为150 和42 的最大公约数，我们可将问题转换为：求一组整数x，y 使得25x+7y=1。

这里我们应用欧拉演段解得该问题，求出所求两数为2 和-7，欧拉演段就不在这里演示。

即6=150×2+42×(-7)，于是x=2，y=-7 为所求。这也是辗转相除法在代数解题中的小应用。

辗转相除是后面才加入教材中的，是算法的经典案例，教学中注重这个内容的深入研究，是对于教学有促进作用的。放眼望去，辗转相除法的应用极其广泛，在各种计算机算法及编程中广泛应用，特别地，在算法学习的研究中更是有着非常重要的地位。另外在高等数学中，它还被用来解丢番图方程，寻找满足中国剩余定理的数，或者求有限域中元素的逆。辗转相除法还可以用来构造连分数，在施图姆定理和一些整数分解算法中也有应用。辗转相除法是现代数论中的基本工具。