LASSO算法在基于自然群体随机交配的多iQTL定位中的应用

黎哲镇，郑珂辉,2，周富杰，叶景山，温永仙

(1.福建农林大学计算机与信息学院；2.福建农林大学生命科学学院,福建 福州 350002)

基因组印迹是指在亲本形成配子或者在合子发育期间，来自双亲的一对等位基因产生了专一性修饰，致使子代细胞中两同源等位基因具有不同表达活性的现象[1]，产生这种差异的基因称为印迹基因(imprinted quantitative trait loci, iQTL).研究[2,3]表明，iQTL可以作为一个数量性状位点及其表达产物显示在一个数量尺度，对iQTL进行定位分析，有助于了解动植物中基因组印迹对复杂性状的作用.有关iQTL的研究早在上个世纪90年代就已经开展，Shete et al[4]提出使用方差分析来对各标记的加性效应、显性效应、印迹效应进行分析；Cui et al[5]提出了一个最大似然方法来测试和估计iQTL的印迹效应；Jiang et al[6]用荷兰牛父本母本和子代的基因型来研究繁殖性状等加性、显性和印迹效应；Meng et al[7]通过使用高通量RNA测序技术，在玉米胚乳中发现了有36个先前未被鉴定的 iQTL.

LASSO算法从2008年开始逐渐被应用到多个位点的QTL研究中，Cai et al[8]将LASSO算法进行了改进，结合贝叶斯算法，提出了采用快速经验贝叶斯LASSO(EBLASSO)检测出更多的QTL效应，包括主位和上位QTL效应、环境效应和基因—环境相互作用效应；Huang et al[9]提出了通过EBLASSO-logistic回归方法进行模拟研究，该方法能够解决主效应和上位效应的二元性状QTL模型；Papachristou et al[10]将LASSO与混合线性模型相结合，试验结果表明该算法能够显著降低假阳性.

对于iQTL定位群体的使用一般采用F2群体和BC1群体，但是这两种群体为临时性群体，有一定的局限性.Wen et al[11]提出了基于永久性F2群体的iQTL定位，研究表明基于imF2群体的iQTL定位，对iQTL的加性、显性和印迹效应的检测可以达到无偏.郑珂晖等[12]提出了基于自然群体随机交配产生的群体的iQTL定位，构建其初步的定位方法，并进行全基因组的单点模拟，结果表明对自然群体随机交配产生的群体进行iQTL定位是可行的.本研究在此基础上利用自然群体随机交配产生的群体进行多iQTL定位研究，应用LASSO算法筛选出基因组范围内具有非零印迹效应点的位置，并且对这些点进行效应值的估计和检验，最后通过计算机模拟来验证该方法的有效性和可行性，为进一步在全基因组范围内进行印迹QTL关联分析提供参考.

1 材料与方法

1.1 试验设计

表1 基因型的频率与虚拟变量取值1)Table 1 Frequencies of genotypes and values of dummy variables

1)μ：群体的均值.a：加性效应.d：显性效应.i：印迹效应.

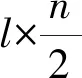
1.2 多iQTL定位的遗传模型

假定控制某一性状的QTL有2个等位基因，Q1的等位基因频率为p，Q2的等位基因频率为q=1-p.在随机交配群体中，考虑加性效应、显性效应和印迹效应，经随机交配后有4种可能的基因型，各自的频率及其虚拟变量的取值参考文献[12]，结果如表1所示.

若φ1、φ2、φ3、φ4分别代表Q1Q1、Q1Q2、Q2Q1、Q2Q24种基因型的效应，则φ1=μ+a，φ2=μ+d+i，φ3=μ+d-i，φ4=μ-a.

根据表1，可以推算出印迹QTL的均值和方差[13]，分别表示为：

M=a(p-q)+2pqd

(1)

VG=[p2a2+pq(d+i)2+pq(d-i)2+q2a2]-[a(p-q)+2dpq]2

=2pq[a+d(q-p)]2+2pqi2+(2pqd)2

(2)

若用等位基因代替效应的平均效应，即A=a+d(q-p)，则方差可以用下式表示：

VG=VA+Vd+Vi

(3)

VA=2pq[a+d(q-p)]2

(4)

Vd=(2pqd)2

(5)

Vi=2pqi2

(6)

式中，VA为加性方差，Vd为显性方差，Vi为印迹方差.

(7)

式中,Vp=VG+Ve，Ve为环境方差.

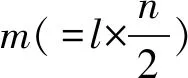
(8)

式中yj为表型值，μ为群体均值，K代表遗传标记的个数，ajk代表第k个标记的加性效应，djk代表第k个标记的显性效应，ijk代表第k个标记的印迹效应，εj代表服从均值为零，方差为Ve的正态分布的随机误差(εj～N(0,Ve))，xjk、zjk、tjk分别代表第k个标记的加性、显性、印迹效应的虚拟变量，根据表1取值.

1.3 多iQTL定位方法

LASSO算法是Tibsirani提出的一种算法[14]，该算法可以对自变量为高维的数据进行压缩筛选，还可以得出其参数估计值.

一般线性模型表示如下：

(9)

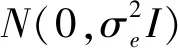
LASSO方法就是线性回归模型中基于惩罚函数的变量选择方法，即在β=arg min‖y-Xβ‖2=(XTX)-1XTy中增加L1惩罚项，LASSO的估计值为：

(10)

上式罚参数λ的调整决定了模型的复杂程度，因此选择合适的罚参数对模型的求解至关重要，其目标是使得模型的预测精度达到最优.惩罚参数的选择方法有赤池信息准则(AIC)、贝叶斯信息准则(BIC)、Cp准则、交叉验证(CV)等方法和广义交叉验证(GCV)，通常采用10折交叉验证(10-fold Cross-Validation)[15]实现罚参数的选择.

对于多iQTL遗传模型(式(8))，运用LASSO算法挑选出s个备选QTL；对于s个变量，重新建立多元线性回归方程：

(11)

运用多元线性回归普通最小二乘法重新进行参数估计.

对印迹QTL存在的检验，假设H0∶a=d=i=0，H1∶a,d,i不全为零，如果仅检验印迹效应，那么假设H0∶i=0，H1∶i≠0，在式(11)计算过程中，采用t检验来检测每个变量，筛选出印迹QTL.

2 结果与分析

2.1 模拟产生的自然群体

采用黄杨岳等[16]的仿真方法产生自然群体基因型数据，在仿真过程中，等位基因频率p服从0.05～0.95的均匀分布，相邻SNPs间的连锁不平衡系数服从0.8～1.0的均匀分布.假设在一条染色体上有800个SNP，在50和500处有印迹QTL且2个位点相互独立.计算机模拟产生50处的第一个QTL，其等位基因频率p为0.47；假设此处的QTL加性效应a为2，显性效应d为1，印迹效应i为1；计算机模拟产生500处的第二个QTL，其等位基因频率p为0.59，假设其加性效应a为1，显性效应d为0，印迹效应i为0.5.对于每个QTL，分别考虑印迹遗传率为0.02、0.05、0.10三种情况.通过计算、模拟产生包含200个个体的自然群体，随机交配1、2、3次，每种情况模拟100次，显著性水平取0.05.由于假设500处点的显性效应d为0，在LASSO运算过程中被压缩为0，故不列入表2中，详细模拟结果见表2.

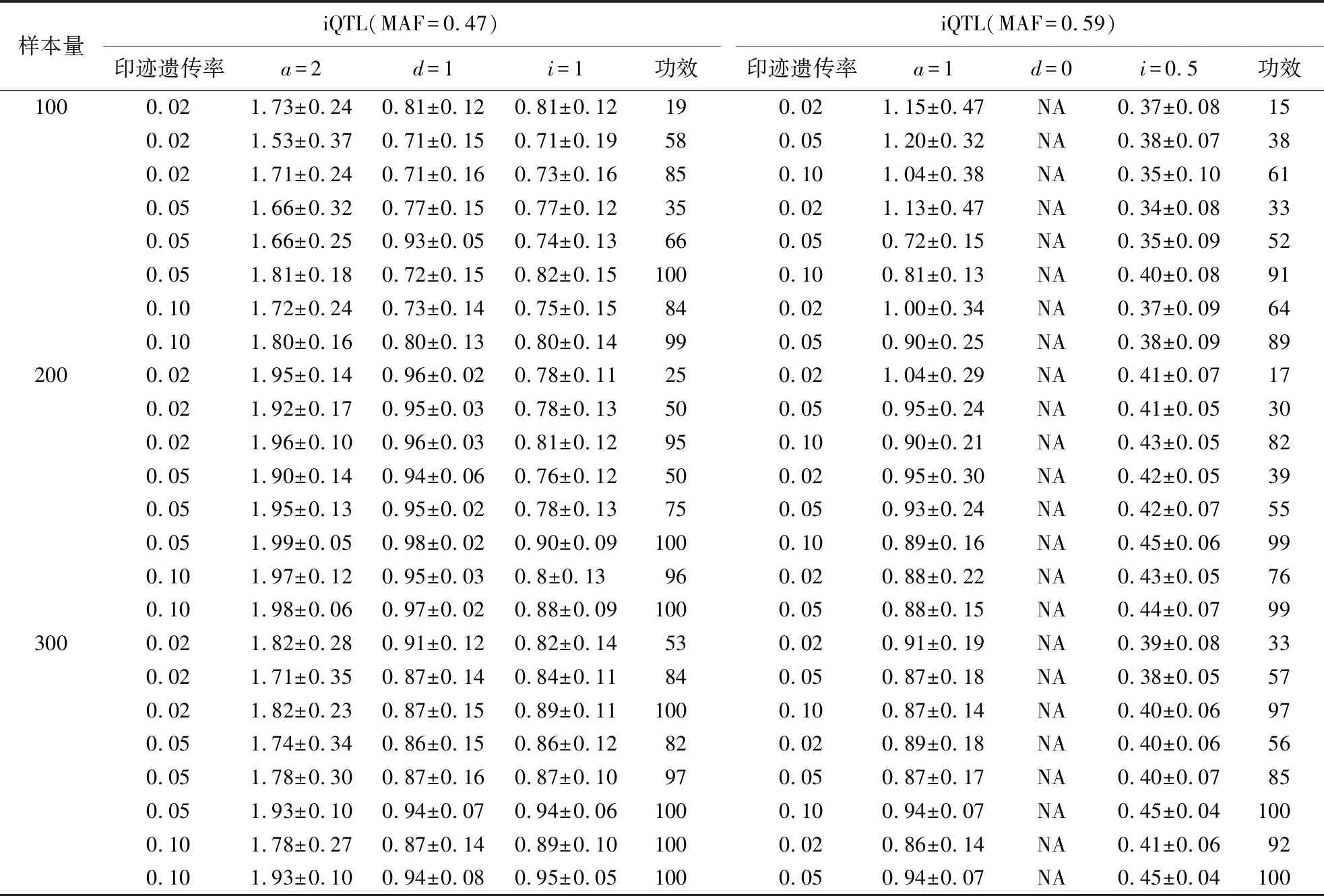
表2 基于LASSO算法的iQTL定位结果Table 2 iQTL mapping based on LASSO algorithm

从表2可以看出，LASSO算法可以精确估计出iQTL的位置与效应值，当遗传率较低时，iQTL的检测功效较低，且估计的标准误会较大；随着遗传率的增加，其检测功效也随之增加，并且参数估计的标准误降低.由此可知遗传率是影响iQTL定位效果的因素之一.从表2还可以看出随着交配次数的增加，iQTL的检测功效也随之增加，参数估计的标准误降低，在遗传率相同的情况下，样本量大的群体，其参数估计的准确度和检测功效都比样本量低的群体高.因此在进行iQTL定位时，要尽量增加交配次数，提高样本量，提升定位的准确性和检测功效.综上所述，LASSO在自然群体中多个iQTL定位是有效的.

2.2 实际水稻基因型数据

表3 印迹类型、简写与参数的设置Table 3 List of imprint types, abbreviations and parameters

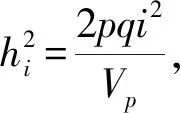
根据上述假设，在随机交配次数为1、2、3次的情况下进行模拟，每种情况模拟100次，显著性水平取0.05.在计算过程中，对于每种类型的iQTL，当遗传效应为零时，LASSO将其效应值压缩为零，故不列入表4中，详细结果见表4.

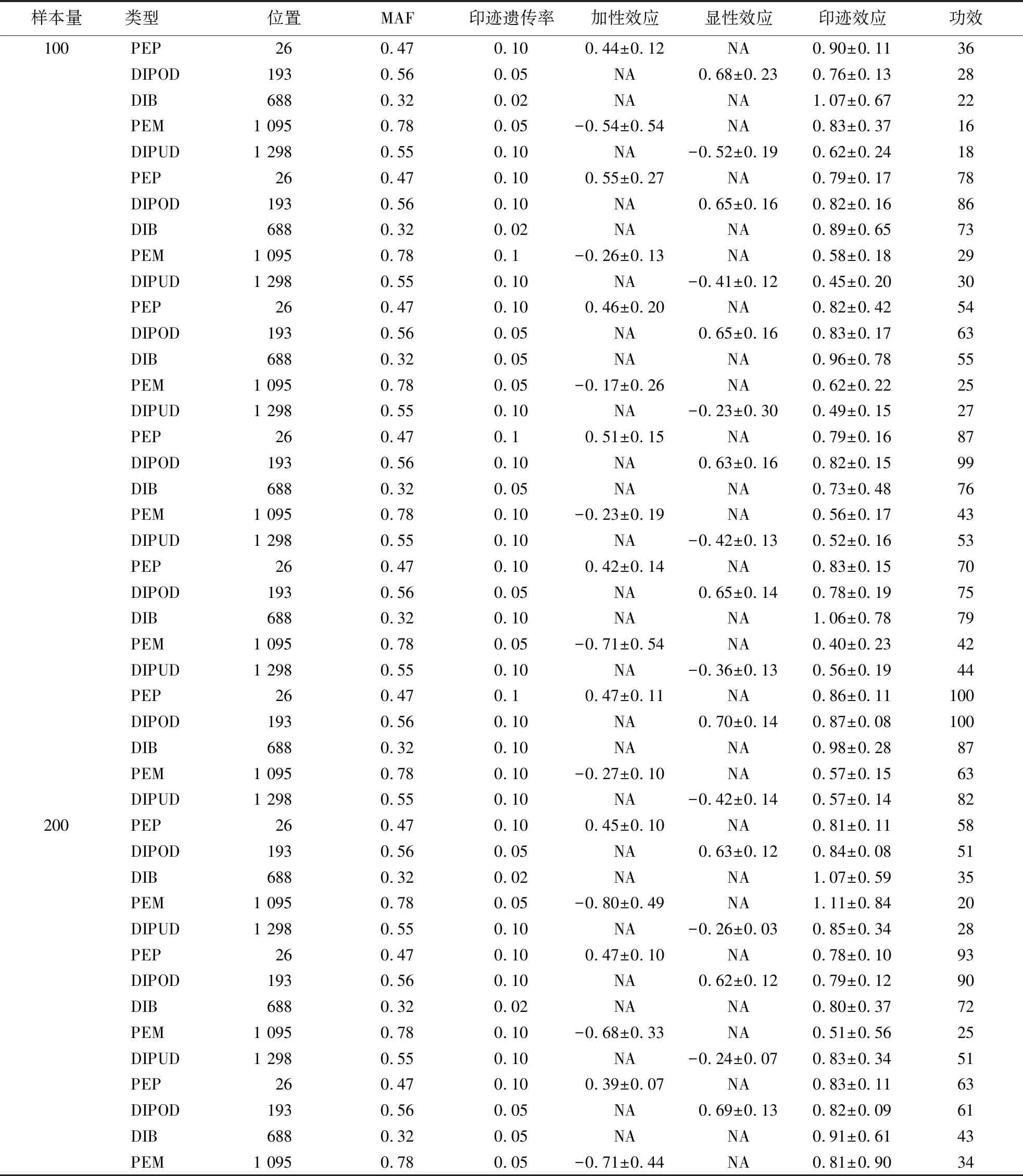
表4 5种不同类型iQTL的定位结果Table 4 iQTL mapping results for 5 imprint types

续表4

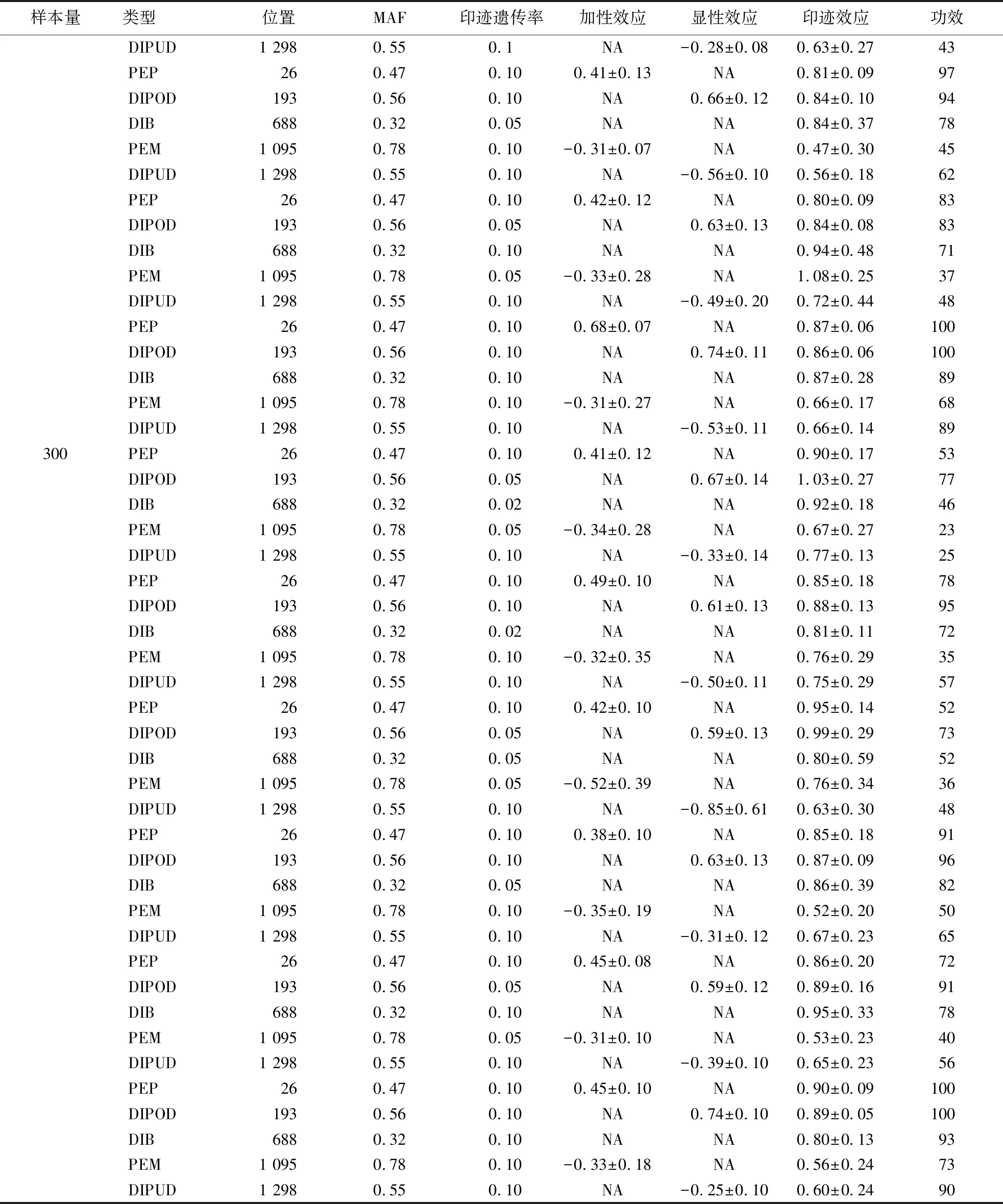
样本量类型位置MAF印迹遗传率加性效应显性效应印迹效应功效DIPUD1 2980.550.1NA-0.28±0.080.63±0.2743PEP260.470.100.41±0.13NA0.81±0.0997DIPOD1930.560.10NA0.66±0.120.84±0.1094DIB6880.320.05NANA0.84±0.3778PEM1 0950.780.10-0.31±0.07NA0.47±0.3045DIPUD1 2980.550.10NA-0.56±0.100.56±0.1862PEP260.470.100.42±0.12NA0.80±0.0983DIPOD1930.560.05NA0.63±0.130.84±0.0883DIB6880.320.10NANA0.94±0.4871PEM1 0950.780.05-0.33±0.28NA1.08±0.2537DIPUD1 2980.550.10NA-0.49±0.200.72±0.4448PEP260.470.100.68±0.07NA0.87±0.06100DIPOD1930.560.10NA0.74±0.110.86±0.06100DIB6880.320.10NANA0.87±0.2889PEM1 0950.780.10-0.31±0.27NA0.66±0.1768DIPUD1 2980.550.10NA-0.53±0.110.66±0.1489300PEP260.470.100.41±0.12NA0.90±0.1753DIPOD1930.560.05NA0.67±0.141.03±0.2777DIB6880.320.02NANA0.92±0.1846PEM1 0950.780.05-0.34±0.28NA0.67±0.2723DIPUD1 2980.550.10NA-0.33±0.140.77±0.1325PEP260.470.100.49±0.10NA0.85±0.1878DIPOD1930.560.10NA0.61±0.130.88±0.1395DIB6880.320.02NANA0.81±0.1172PEM1 0950.780.10-0.32±0.35NA0.76±0.2935DIPUD1 2980.550.10NA-0.50±0.110.75±0.2957PEP260.470.100.42±0.10NA0.95±0.1452DIPOD1930.560.05NA0.59±0.130.99±0.2973DIB6880.320.05NANA0.80±0.5952PEM1 0950.780.05-0.52±0.39NA0.76±0.3436DIPUD1 2980.550.10NA-0.85±0.610.63±0.3048PEP260.470.100.38±0.10NA0.85±0.1891DIPOD1930.560.10NA0.63±0.130.87±0.0996DIB6880.320.05NANA0.86±0.3982PEM1 0950.780.10-0.35±0.19NA0.52±0.2050DIPUD1 2980.550.10NA-0.31±0.120.67±0.2365PEP260.470.100.45±0.08NA0.86±0.2072DIPOD1930.560.05NA0.59±0.120.89±0.1691DIB6880.320.10NANA0.95±0.3378PEM1 0950.780.05-0.31±0.10NA0.53±0.2340DIPUD1 2980.550.10NA-0.39±0.100.65±0.2356PEP260.470.100.45±0.10NA0.90±0.09100DIPOD1930.560.10NA0.74±0.100.89±0.05100DIB6880.320.10NANA0.80±0.1393PEM1 0950.780.10-0.33±0.18NA0.56±0.2473DIPUD1 2980.550.10NA-0.25±0.100.60±0.2490

从模拟结果来看，当遗传率较低时，iQTL的检测功效较低，且估计的标准误会较大，随着遗传率的增加，其检测功效也随之增大.在遗传率相同的情况下，样本量大的群体的参数估计的准确度和检测功效都比样本量低的群体要高.但是PEM和DIPUD的参数估计值的准确度和检测功效跟PEP、DIPOD和DIB对比都较低，其原因可能是负的加性效应与显性效应对印迹效应的估计产生了影响，说明遗传效应影响了参数估计和检测功效.通过模拟试验发现，当基因频率p与q相差较大时，效应值的估计标准的误差较大.因此在进行iQTL定位时，要尽量增加交配次数，提高样本量，减小效应方向以及基因频率p与q差异的影响，使iQTL的定位准确性和检测功效得到提升.

3 小结

本研究应用LASSO算法进行多iQTL定位，在不考虑如群体结构等干扰的影响下进行模拟研究，结果表明 iQTL定位方法的参数估计较为精确，且检测功效也较好，这也是LASSO算法的优势.然而在模拟过程中发现，当iQTL的各种遗传效应较小时，LASSO存在过度压缩的问题，即将各种遗传效应压缩为零，从而降低了检测iQTL的精度.

从本研究的模拟结果也可看出，通过自然群体随机交配的群体进行iQTL分析时，可以通过增加交配次数来提升样本量，以得到更高的检测功效和更精确的参数估计.但是对于复杂群体结构的群体时，必须考虑到群体结构的影响.